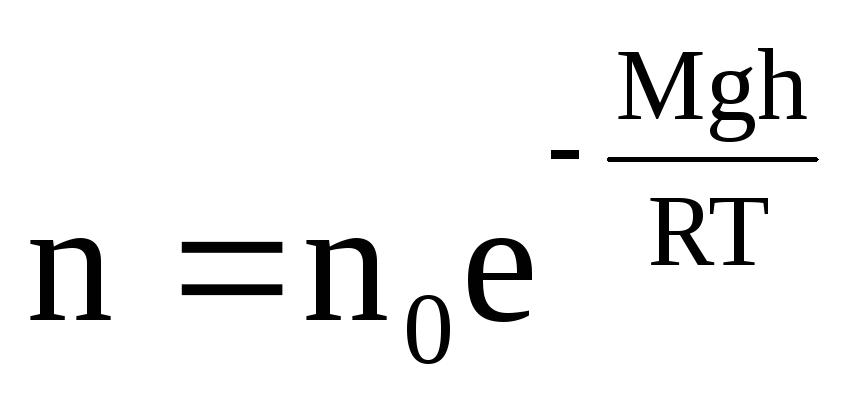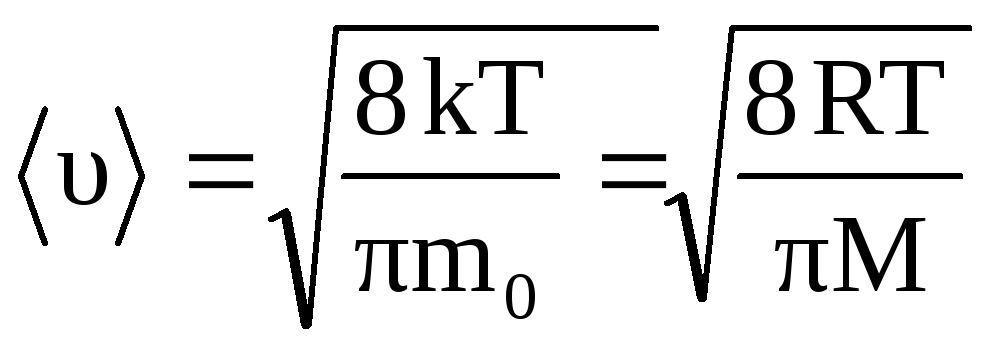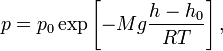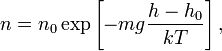- 7. Барометрическая формула. Закон распределения Больцмана.
- 8. Определение числа Авогадро из опыта Перрена.
- 1. 4. Барометрическая формула. @
- 1. 5. Закон Больцмана о распределении частиц во внешнем потенциальном поле. @
- 1. 6. Распределение Максвелла молекул идеального газа по скоростям. @
- Барометрическая формула. Распределение Больцмана
7. Барометрическая формула. Закон распределения Больцмана.
При выводе основного уравнения молекулярно-кинетической теории газов предполагалось, что на молекулы газа внешние силы не действуют, поэтому молекулы равномерно распределены по объему. Если гав находится в силовом поле, то существуют силы, которые сообщают хаотически движущимся молекулам направленное движение.
Молекулы газа, находящиеся в поле тяготения, участвуют в тепловом движении и испытывают действие силы тяжести. Тяготение и тепловое движение приводят к состоянию газа, при котором наблюдается убыль концентрации и давления газа с возрастанием высоты над землей.
Выведем закон изменения давления с высотой, предполагая, что поле тяготения однородно, температура постоянна и масса всех молекул одинакова и равна m0.
Атмосферное давление на некоторую площадку S обусловлено весом столба воздуха над этой площадкой (т.е. действием силы тяжести). Пусть на высоте h – давление р, а при h=0 – p=p0. Рассмотрим изменение давления элемента “столба” высотой dh, в пределах которого концентрацию можно считать постоянной. Убыль давления в пределах dh: .
Произведя разделение переменных: , получим
Зависимость давления атмосферы от высоты над уровнем моря при постоянной температуре называют барометрической формулой.
Пользуясь барометрической формулой , можно получить закон изменения концентрации с высотой. Приняв во внимание и , где n и n0 – концентрация молекул на высоте h и h0=0 и подставляя р и р0 в барометрическую формулу, получим закон распределения концентраций по высоте: ,
Полученное распределение Больцмана справедливо для поля тяготения, для которого – потенциальная энергия на высоте h (на разной высоте молекула обладает различным запасом потенциальной энергии). Однако оно справедливо и для идеального газа, находящегося в любом другом потенциальном поле:
распределение Больцмана в поле с потенциальной энергией U .
При Т , nn0, то есть происходит выравнивание концентрации газа по всему объему, занимаемому газом. При Т 0, n 0, то есть все молекулы опустятся на поверхность Земли (если речь идет об атмосфере).
8. Определение числа Авогадро из опыта Перрена.
Перрен исходил из того, что выводы из молекулярно-кинетической теории справедливы не только для атомов и молекул, но и для броуновских частиц. В подтверждение было показано, что измеренное значение кинетической энергии броуновской частицы действительно оказалось равным .
Перрен предположил, что на “газ” броуновских частиц может быть распространен барометрический закон. Перрен приготовил эмульсию из некоторой смолы (гуммигут — млечный сок деревьев, растущих в Ост.Индии и Цейлоне). Броуновскими частицами были шарики из этой смолы размерами (0,20,5) мкм, причем отделялись (отфильтровывались) частицы с одинаковыми размерами. Эмульсия помещалась в кювету, которая наблюдалась в микроскоп.. Глубина поля зрения порядка одного микрона. Подсчитывалось число частиц на этой высоте. Подсчитывалось число частиц на высотах h1 и h2.
С учетом Архимедовой силы (на частицу, имеющую плотность порядка =1,2 г/см 3 и находящуюся в воде с близкой по величине плотностью ’=1 г/см 3 , действует выталкивающая сила): .
Таким образом, из эксперимента находится величина k по формуле:
Число Авогадро вычисляется из : .
Это был один из первых методов вычисления числа Авогадро. Оно оказалось равным: NA 6,8.10 23 моль -1 . Таким образом, значение, полученное Перреном, находится в согласии с другими полученными значениями, следовательно к броуновским частицам можно применить распределение Больцмана.
Источник
1. 4. Барометрическая формула. @
При выводе основного уравнения молекулярно-кинетической теории предполагалось, что если на молекулы газа не действуют внешние силы, то молекулы равномерно распределены по объему. Однако молекулы любого газа находятся в потенциальном поле тяготения Земли. Тяготение, с одной стороны, и тепловое движение молекул, с другой, приводят к некоторому стационарному состоянию газа, при котором концентрация молекул газа и его давление с высотой убывают. Выведем закон изменения давления газа с высотой, предполагая при этом, что поле тяготения однородно, температура постоянна и масса всех молекул одинакова. Если атмосферное давление на высоте hравно р, то на высотеh+dhоно равно р +dp(рис.1.2). Приdh> 0,dр < 0, т.к. давление с высотой убывает. Разность давлений р и (р +dр) равна гидростатическому давлению столба газа авсd, заключенного в объеме цилиндра высотойdhи площадью с основанием равным единице. Это запишется в следующем виде:p- (p+dp) =gρdh, -dp=gρdhилиdp= ‑gρdh, гдеρ– плотность газа на высотеh. Воспользуемся уравнением состояния идеального газа рV=mRT/Mи выразим плотностьρ=m/V=pM/RT. Подставим это выражение в формулу дляdр:
Интегрирование данного уравнения дает следующий результат: Здесь С – константа и в данном случае удобно обозначить постоянную интегрирования черезlnC. Потенцируя полученное выражение, находим, что
При условии h=0 получим, что С=р0, где р0-давление на высотеh=0.
Данное выражение называется барометрической формулой. Она позволяет найти атмосферное давление в зависимости от высоты, или высоту, если известно давление.
Зависимость давления от высоты демонстрирует рисунок 1.3. Прибор для определения высоты над уровнем моря называется высотомером или альтиметром. Он представляет собой барометр, проградуированный в значениях высоты.
1. 5. Закон Больцмана о распределении частиц во внешнем потенциальном поле. @
Если воспользоваться выражением р = nkT, то можно привести барометрическую формулу к виду:
здесьn– концентрация молекул на высотеh,n0– то же у поверхности Земли. Так как М =m0NA , гдеm0 – масса одной молекулы, аR=kNA, то мы получим П =m0gh– это потенциальная энергия одной молекулы в поле тяготения. ПосколькуkT~‹εпост›, то концентрация молекул на определенной высоте зависит от соотношения П и ‹εпост›
Полученное выражение называется распределением Больцмана для внешнего потенциального поля. Из него следует, что при постоянной температуре плотность газа (с которой связана концентрация) больше там, где меньше потенциальная энергия его молекул.
1. 6. Распределение Максвелла молекул идеального газа по скоростям. @
При выводе основного уравнения молекулярно-кинетической теории отмечалось, что молекулы имеют различные скорости. В результате многократных соударений скорость каждой молекулы меняется со временем по модулю и по направлению. Из-за хаотичности теплового движения молекул все направления являются равновероятными, а средняя квадратичная скорость остается постоянной. Мы можем записать
Постоянство ‹υкв› объясняется тем, что в газе устанавливается стационарное, не меняющееся со временем распределение молекул по скоростям, которое подчиняется определенному статистическому закону. Этот закон теоретически был выведен Д.К.Максвеллом. Он рассчитал функциюf(), называемую функцией распределения молекул по скоростям. Если разбить диапазон всех возможных скоростей молекул на малые интервалы, равныеd, то на каждый интервал скорости будет приходиться некоторое число молекулdN(), имеющих скорость, заключенную в этом интервале (Рис.1.4.).
Функция f(v) определяет относительное число молекул, скорости которых лежат в интервале от до + d. Это число — dN()/N= f()d.Применяя методы теории вероятностей, Максвелл нашел вид для функции f()
Данное выражение — это закон о распределении молекул идеального газа по скоростям.Конкретный вид функции зависит от рода газа, массы его молекул и температуры (рис.1.5). Функция f()=0 при =0 и достигает максимума при некотором значении в, а затем асимптотически стремится к нулю. Кривая несимметрична относительно максимума. Относительное число молекул dN()/N, скорости которых лежат в интервале d и равное f()d, находится как площадь заштрихованной полоски основанием dv и высотой f(), показанной на рис.1.4. Вся площадь, ограниченная кривой f() и осью абсцисс равна единице, потому что, если просуммировать все доли молекул, имеющих всевозможные значения скорости, то получается единица. Как показано на рис.1.5, с ростом температуры кривая распределения смещается вправо, т.е. растет число быстрых молекул, но площадь под кривой остается постоянной, т.к. N = const.
Скорость в, при которой функция f() достигает максимума, называется наиболее вероятной скоростью. Из условия равенства нулю первой производной функцииf(v) ′ = 0 следует, что
На рисунке 1.4. отмечена еще одна характеристика – средняя арифметическая скорость молекулы. Она определяется по формуле:
Опыт, проведенный немецким физиком О.Штерном, экспериментально подтвердил справедливость распределения Максвелла (рисунок 1.5.). Прибор Штерна состоит из двух коаксиальных цилиндров. Вдоль оси внутреннего цилиндра со щелью проходит платиновая проволока, покрытая слоем серебра. Если пропустить по проволоке ток,она нагревается и серебро испаряется. Атомы серебра, вылетая через щель, попадают на внутреннюю поверхность второго цилиндра. Если прибор будет вращаться, то атомы серебра осядут не против щели, а сместятся от точки О на некоторое расстояние. Исследование количество осадка позволяет оценить распределение молекул по скоростям. Оказалось, что распределение соответствует максвелловскому.
Источник
Барометрическая формула. Распределение Больцмана
Барометрическая формула — зависимость давления или плотности газа от высоты в поле силы тяжести.
Для идеального газа, имеющего постоянную температуру 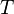
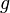
где 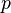
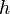
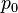
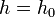
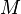
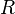
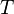
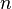
где 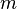
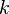
Барометрическая формула может быть получена из закона распределения молекул идеального газа по скоростям и координатам в потенциальном силовом поле (см. Статистика Максвелла — Больцмана). При этом должны выполняться два условия: постоянство температуры газа и однородность силового поля. Аналогичные условия могут выполняться и для мельчайших твёрдых частичек, взвешенных в жидкости или газе. Основываясь на этом, французский физик Ж. Перрен в 1908 году применил барометрическую формулу к распределению по высоте частичек эмульсии, что позволило ему непосредственно определить значение постоянной Больцмана.
Барометрическая формула показывает, что плотность газа уменьшается с высотой по экспоненциальному закону. Величина 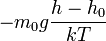
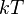
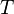
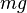
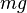
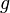
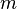
Следовательно, в смеси газов, находящейся в поле тяжести, молекулы различной массы по-разному распределяются по высоте.
Реальное распределение давления и плотности воздуха в земной атмосфере не следует барометрической формуле, так как в пределах атмосферы температура и ускорение свободного падения меняются с высотой и географической широтой. Кроме того, атмосферное давление увеличивается с концентрацией в атмосфере паров воды.
Барометрическая формула лежит в основе барометрического нивелирования — метода определения разности высот 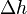
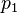
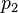
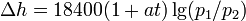
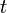
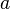
В присутствии гравитационного поля (или, в общем случае, любого потенциального поля) на молекулы газа действует сила тяжести. В результате, концентрация молекул газа оказывается зависящей от высоты в соответствии с законом распределения Больцмана:
где n — концентрация молекул на высоте h, n0 — концентрация молекул на начальном уровне h = 0, m — масса частиц, g — ускорение свободного падения, k — постоянная Больцмана, T — температура.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Источник