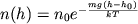Зависимость давления воздуха от высоты над уровнем моря

Атмосферное давление

Давление в каждой точке атмосферы определяется массой вышестоящего столба воздуха с основанием, равным единице. Атмосферное давление с увеличением высоты уменьшается, так как над точкой располагается столбец воздуха с меньшей высотой и воздух начинается разряжаться. Примерно на 12 метров подъема вверх атмосферное давление понижается на 1 мм. рт. ст. до высоты 2000 метров. В среднем, атмосферное давление на Земле равняется 760 мм рт. ст.

Атмосферное давление, равное давлению столба ртути высотой 760 мм при температуре 0 градусов Целься считается нормальным атмосферным давлением. 760 мм рт. ст. равняется 101 300 Па = 1013 гПа.

СЛОЖНА-А-А 🙀 Ты же знаешь, что если не разобраться в теме сейчас, то потом придется исправлять оценки. Беги на бесплатное онлайн-занятие с репетитором (подробности тут + 🎁).

Как меняется, от чего зависят показания

Как мы знаем, атмосфера — это газовая оболочка Земли и как мы тоже знаем, газы сильно сжимаемы. Если газ сильнее сжат, то плотность его будет больше, а следовательно, и давление тоже. Слои воздуха у поверхности Земли сжаты всеми слоями воздуха. По мере подъема вверх от поверхности Земли, слабее будет сжиматься воздух, следовательно, плотность и давление будет меньше.

Чем выше местность над уровнем моря, тем атмосферное давление меньше. Чем ниже местность над уровнем моря, тем атмосферное давление больше.

В пример можно привести воздушный шарик, наполненный водородом. У поверхности Земли давление внутри шарика будет равным давлению на поверхности Земли. По мере отдаления от поверхности Земли, атмосферное давление будет меньше воздействовать на шар, так как чем выше от поверхности Земли, тем меньше плотность воздуха. В результате давление воздуха внутри шарика будет становится больше атмосферного давления, что приведет к разрыву шарика.

Примеры задач по физике для 7 класса

Высота горы Эверест равняется 8800 метров над уровнем моря. Рассчитайте атмосферное давление на вершине горы. Дано: Ответ: высота равняется 10,34 метра.

С какой силой давит воздух на поверхность крышки ящика площадью 1,5\;м^2 ? Решение: Ответ: сила равна 152 кН.

Вычислить примерную высоту телевизионной башни в Останкино. Атмосферное давление у ее подножия равна 755 мм рт. ст., а на вершине равна 710 мм рт. ст. Решение: Задача

Стрелка Барометра-анероида показывает давление 1013 гПа. Соответствуя этому показанию, определите какая высота столба ртути будет в трубке Торричелли, установленной вертикально. Дано:

Молодец! Раз ты дочитал это до конца, вероятно, ты все отлично усвоил. Но если вдруг что-то еще непонятно — попробуй онлайн-занятие с репетитором (подробности тут + 🎁).

Учитель непонятно объясняет предмет?

Источник

Как с высотой изменяется атмосферное давление. Формула, график

Не все знают, что на разной высоте давление атмосферы отличается. Существует даже специальный прибор для измерения и давления, и высоты. Называется он барометр-альтиметр. В статье мы подробно изучим, как с высотой изменяется атмосферное давление и при чем тут плотность воздуха. Рассмотрим эту зависимость на примере графика.

Давление атмосферы на разных высотах

Атмосферное давление зависит от высоты. При ее увеличении на 12 м давление уменьшается на 1 мм ртутного столба. Этот факт можно записать с помощью такого математического выражения: ∆h/∆P=12 м/мм рт. ст. ∆h — это изменение высоты, ∆P — изменение атмосферного давления при изменении высоты на ∆h. Что из этого следует?

Из формулы видно, как с высотой изменяется атмосферное давление. Значит, если мы поднимемся на 12 м, то АД уменьшится на 12 мм ртутного столба, если на 24 м — то на 2 мм ртутного столба. Таким образом, измеряя атмосферное давление, можно судить о высоте.

Миллиметры ртутного столба и гектопаскали

В некоторых задачах давление выражается не в миллиметрах ртутного столба, а в паскалях или гектопаскалях. Запишем вышеприведенное соотношение для случая, когда давление выражено в гектопаскалях. 1 мм рт. ст. =133,3 Па =1,333 гПа.

Теперь выразим соотношение высоты и атмосферного давления не через миллиметры ртутного столба, а через гектопаскали. ∆h/∆P=12 м/1,333 гПа. После вычисления получим: ∆h/∆P=9 м/гПа. Выходит, что когда мы поднимаемся на 9 метров, то давление уменьшается на один гектопаскаль. Нормальное давление — это 1013 гПа. Округлим 1013 до 1000 и примем, что на поверхности Земли именно такое АД.

Если мы поднимаемся на 90 м, как с высотой изменяется атмосферное давление? Оно уменьшается на 10 гПа, на 90 м — на 100 гПа, на 900 м — на 1000 гПа. Если на земле давление в 1000 гПа, а мы поднялись на 900 м вверх, то атмосферное давление стало нулевым. Так что, получается что атмосфера заканчивается на девятикилометровой высоте? Нет. На такой высоте есть воздух, там летают самолеты. Так в чем же дело?

Связь плотности воздуха и высоты. Особенности

Как с высотой изменяется атмосферное давление вблизи поверхности Земли? На этот вопрос уже ответила картинка выше. Чем больше высота, тем меньше плотность воздуха. Покуда мы находимся недалеко от поверхности земли, изменение плотности воздуха незаметно. Поэтому на каждую единицу высоты давление уменьшается примерно на одно и тоже значение. Два записанные нами ранее выражения нужно воспринимать как правильные, только если мы находимся недалеко от поверхности Земли, не выше 1-1,5 км.

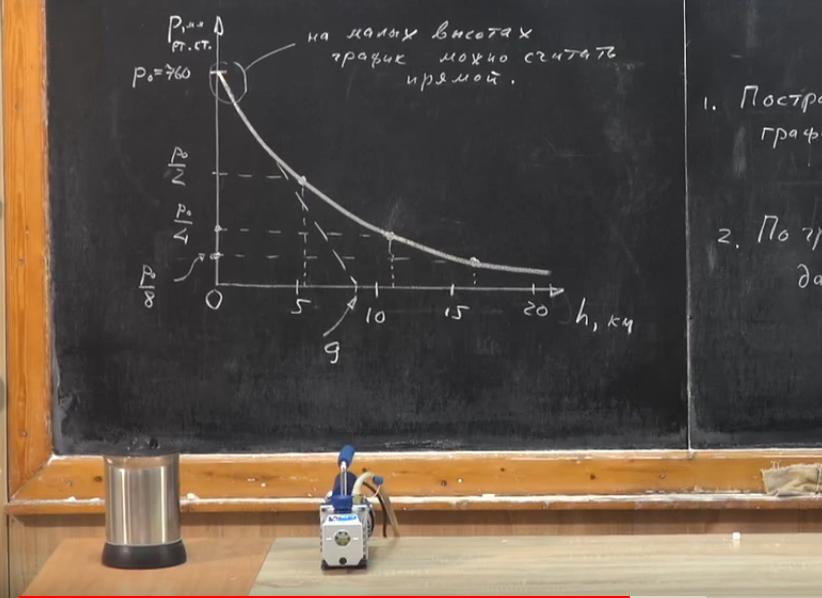
График, показывающий как атмосферное давление изменяется с высотой

Теперь перейдем к наглядности. Построим график зависимости давления атмосферы от высоты. При нулевой высоте P₀=760мм рт. ст. Из-за того, что с ростом высоты давление уменьшается, атмосферный воздух будет менее сжат, его плотность станет меньше. Поэтому на графике зависимость давления от высоты не будет описываться прямой линией. Что это значит?

Как с высотой изменяется атмосферное давление? Над поверхностью земли? На высоте 5,5 км оно уменьшается в 2 раза (Р₀/2). Оказывается, что если мы поднимемся еще на такую же высоту, то есть на 11 км, давление уменьшится еще вдвое и будет равно Р₀/4 и т. д.

Соединим точки, и мы увидим, что график — это не прямая, а кривая. Почему, когда мы записывали соотношение зависимости, складывалось впечатление, что на высоте 9 км атмосфера заканчивается? Мы считали, что график является прямой на любых высотах. Это было бы так, если бы атмосфера была жидкой, то есть если бы ее плотность была постоянной.

Важно понимать, что этот график является лишь фрагментом зависимости на малых высотах. Ни на какой точке этой линии давление не снижается до нуля. Даже в глубоком космосе существуют молекулы газов, которые, правда, не имеют отношение к земной атмосфере. Ни в одной точке Вселенной не существует абсолютного вакуума, пустоты.

Источник

13. Зависимость давления атмосферного воздуха от высоты, барометрическая формула (с выводом!). Графики зависимости давления и концентрации молекул от высоты при различных температурах.

Атмосферное давление — очень изменчивый метеоэлемент. Из его определения следует, что оно зависит от высоты соответствующего столба воздуха, его плотности, от ускорения силы тяжести, которая меняется от широты места и высоты над уровнем моря.1 гПа = 0,75 мм рт. ст. Или 1 мм рт. ст. = 1,333 гПа (133,322 Па).

Барометрическая формула — зависимость давления или плотности газа от высоты в поле тяжести.

Для идеального газа, имеющего постоянную температуру и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения одинаково), барометрическая формула имеет следующий вид:

где P— давление газа в слое, расположенном на высоте h — p0 давление на нулевом уровне (h=h0), M — молярная масса газа,R — газовая постоянная, T — абсолютная температура. Из барометрической формулы следует, что концентрация молекул (или плотность газа) убывает с высотой по тому же закону:

Где m — масса молекулы газа, K — постоянная Больцмана.

Вывод: Следовательно, в смеси газов, находящейся в поле тяжести, молекулы различной массы по-разному распределяются по высоте.

Графики зависимости давления и концентрации молекул от высоты при различных температурах.

14. Барометрическая формула как частный случай распределения Больцмана. Нормировка распределения Больцмана. Примеры использования функции распределения Больцмана.

БАРОМЕТРИЧЕСКАЯ ФОРМУЛА — определяет зависимость от высоты h плотности n или давления p идеального изотермического газа, находящегося в гидростатическом равновесии в однородном поле силы тяжести. Высота h отсчитывается в направлении, противоположном ускорению силы тяжести g. Б. ф. явл. частным случаем Больцмана распределения, обычно используется для описания атмосфер космич. тел (планет, звёзд). Для плотности Б. ф. можно записать в виде:

(1a)

(1б)

где n0 и p0 — плотность п давление на нек-ром начальном уровне h0, m — масса частицы газа. Иногда вместо m удобнее пользоваться молекулярной массой m = m/mu (mu- атомная единица массы), при этом в показателе степени вместо mg/kT следует писать mg/RT, где R — газовая постоянная.

Распределение Больцмана — распределение вероятностей различных энергетических состояний идеальной термодинамической системы (идеальный газ атомов или молекул) в условиях термодинамического равновесия; открыто Л. Больцманом в 1868—1871.

Согласно распределению Больцмана среднее число частиц с полной энергией Ei равно

где Ni — кратность состояния частицы с энергией Ei — число возможных состояний частицы с энергией Ei. Постоянная Z находится из условия, что сумма ni по всем возможным значениям i равна заданному полному числу частиц n в системе (условие нормировки):

Пример: При бросании монеты на твердую горизонтальную поверхность, неясно, как она ляжет: цифрой вверх или гербом. Известно, что вероятности этих событий, при определенных условиях, равны 1/2. При бросании игральной кости нельзя с уверенностью сказать, какая из шести цифр окажется на верхней грани. Вероятность выпадения каждой из цифр при определенных предположениях (кость – однородный куб без сколотых ребер и вершин падает на твердую, гладкую горизонтальную поверхность) равна 1/6.

15. Процессы переноса: диффузия, теплопроводность, вязкость. Дифференциальные уравнения процессов переноса.

Диффузия (лат. diffusio — распространение, растекание, рассеивание, взаимодействие) — процесс взаимного проникновения молекул одного вещества между молекулами другого, приводящий к самопроизвольному выравниванию их концентраций по всему занимаемому объёму.

Теплопрово́дность — это перенос тепловой энергии структурными частицами вещества (молекулами, атомами, ионами) в процессе их теплового движения. Такой теплообмен может происходить в любых телах с неоднородным распределением температур, но механизм переноса теплоты будет зависеть от агрегатного состояния вещества. Явление теплопроводности заключается в том, что кинетическая энергия атомов и молекул, которая определяет температуру тела, передаётся другому телу при их взаимодействии или передаётся из более нагретых областей тела к менее нагретым областям. Иногда теплопроводностью называется также количественная оценка способности конкретного вещества проводить тепло.

Вя́зкость (вну́треннее тре́ние) — одно из явлений переноса, свойство текучих тел (жидкостей и газов) оказывать сопротивление перемещению одной их части относительно другой. В результате происходит рассеяние в виде тепла работы, затрачиваемой на это перемещение.

Дифференциальные уравнения процессов переноса.

Источник