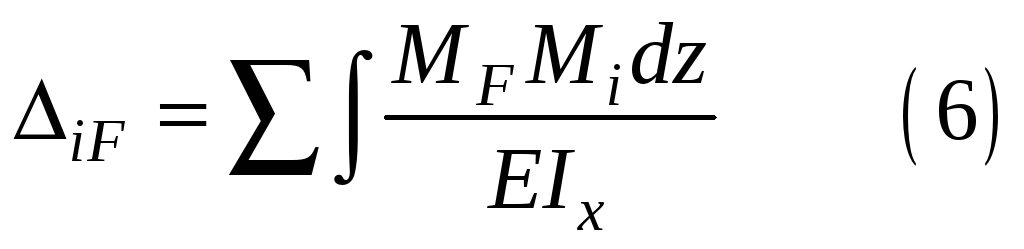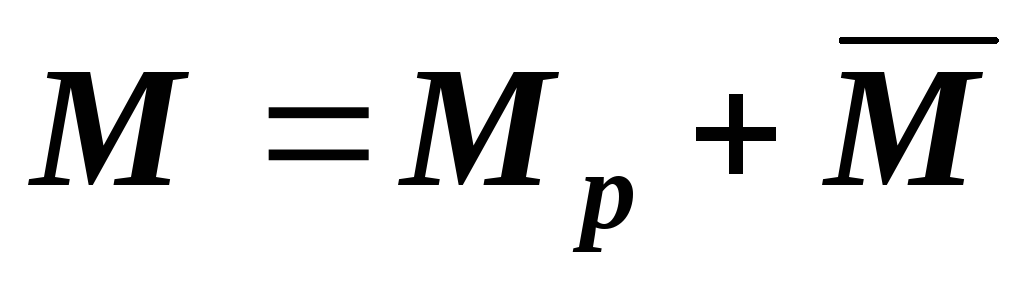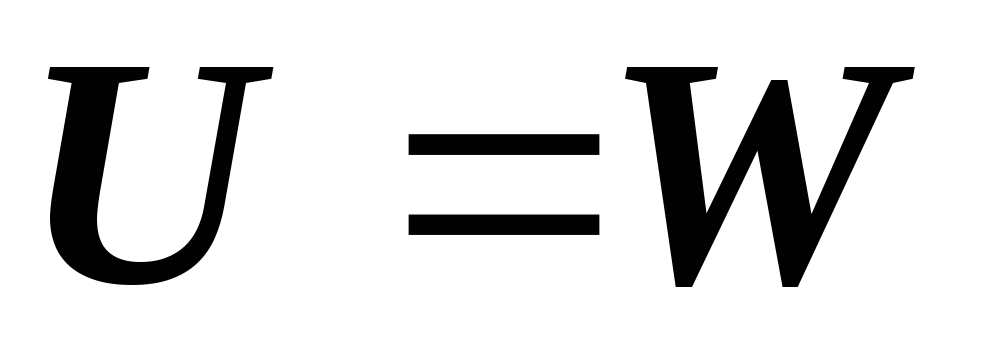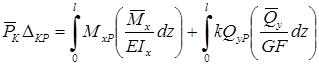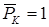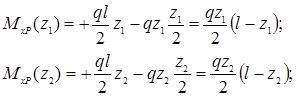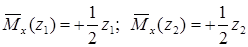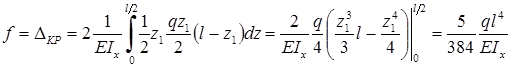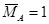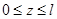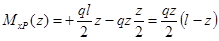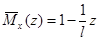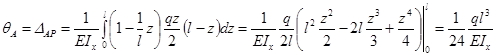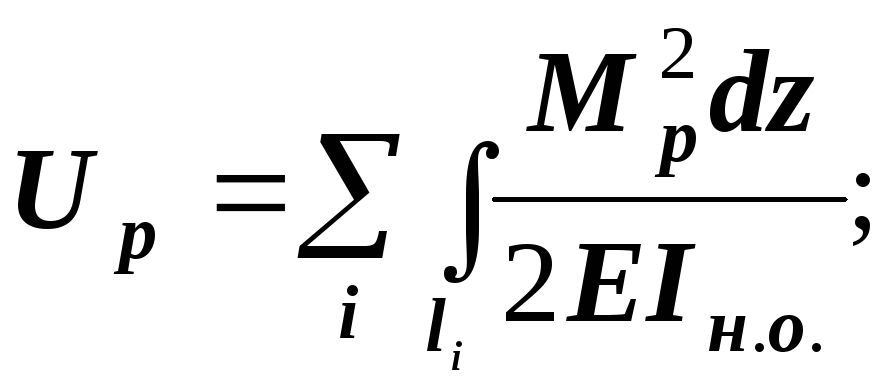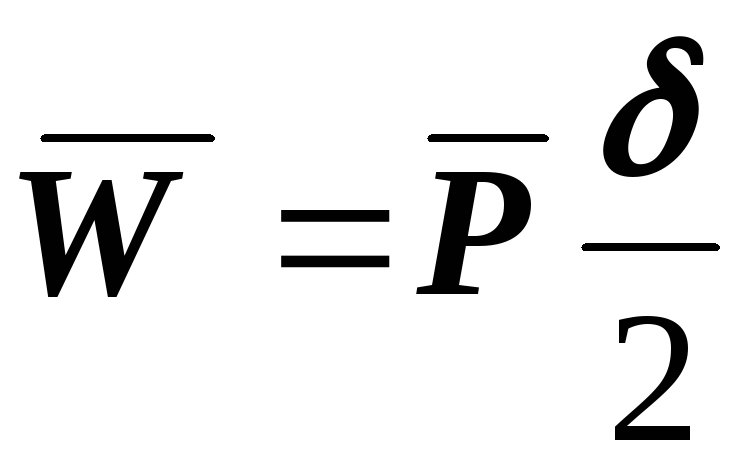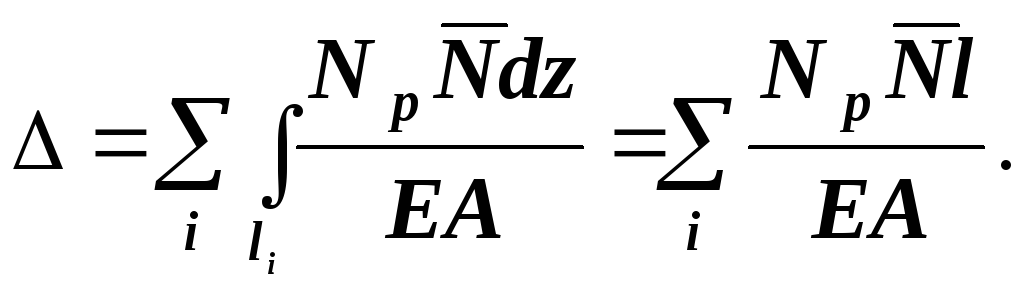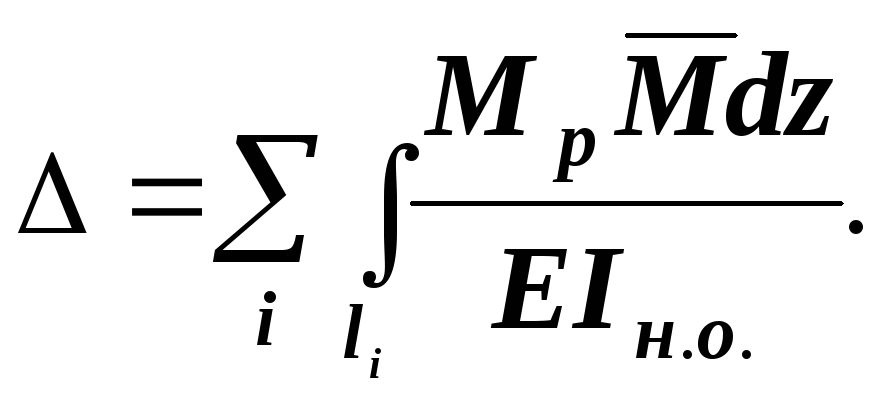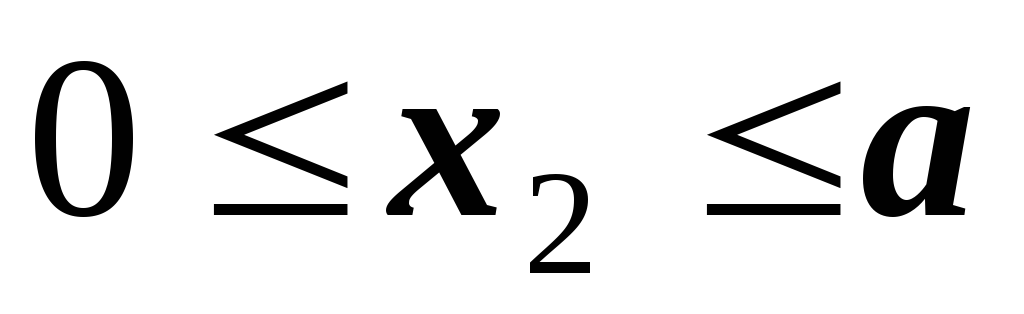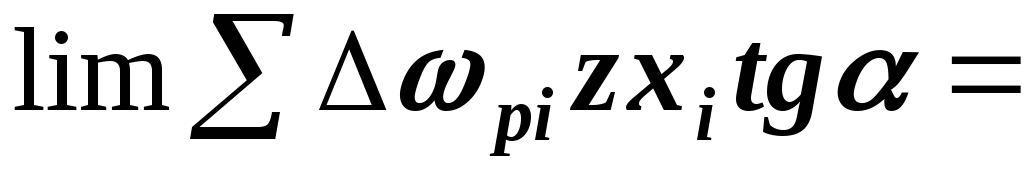Вывод интеграла мора сопромат

Метод Мора. Интеграл Мора

Теорема Кастельяно дала нам возможность определять перемещения. Эту теорему используют для отыскания перемещений в пластинках, оболочках. Однако, вычисление потенциальной энергии громоздкая процедура и мы сейчас наметим более простой и наиболее общий путь определения перемещений в стержневых системах.

Пусть задана произвольная стержневая система и нам нужно определить в ней перемещение точки по направлению , вызванное всеми силами системы —

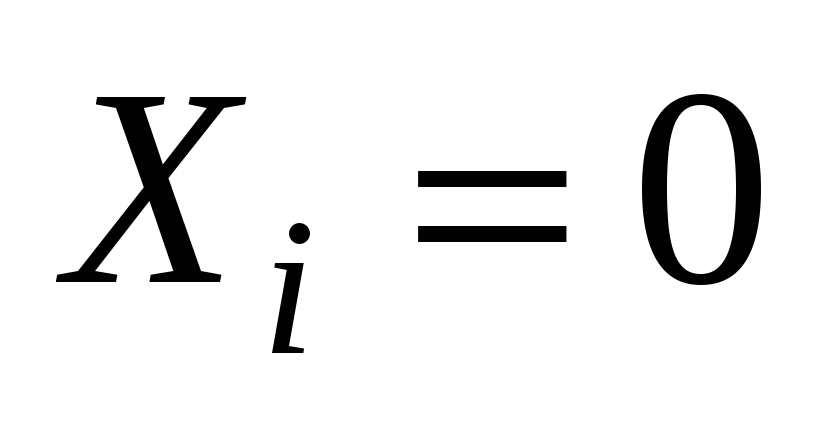
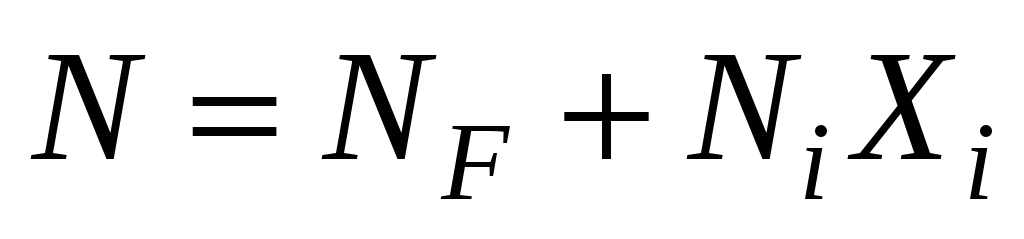
Т.к. в общем случае в системе нет силы, приложенной по направлению искомого перемещения, то воспользоваться теоремой Кастельяно нельзя. Добавим к числу прочих сил силу , приложенную к точке и действующую в направлении . Тогда внутренние силовые факторы в системе можно выразить

, где — внутренние силовые факторы в системе от действующих сил;

— внутренние силовые факторы от силы .

Внесем эти выражения в (3)

По теореме Кастельяно:

Учтя, что

получаем выражение:

называемое интегралом Мора.

Для того, чтобы определить перемещение с помощью метода Мора, необходимо:

1) Определить внутренние силовые факторы в системе от заданных сил.

2) Приложить по направлению искомого перемещения единичную обобщенную силу (единичную силу для определения линейного перемещение, пару сил с моментом равным единице для определения углового перемещения и определить внутренние силовые факторы от единичной силы.

3) Подставить полученные ранее выражения в интеграл Мора и определить перемещение.

Для систем, работающих на изгиб: балок, рам, влияние нормальных сил на величину перемещения незначительно и интеграл Мора в этом случае выглядит:

Источник

4. Интеграл Мора для вычисления перемещений

Вывод формулы проводится для случая плоского изгиба, соответственно учитывается только изгибающий момент . В общем случае нагружения рассуждения аналогичны.

Задана произвольная упругая система, загруженная силами . Требуется определить перемещение произвольной точки в заданном направле-

нии .

Для вывода формулы кроме заданной рассмотрим вспомогательную единичную систему, которая представляет собой заданную упругую систему (рис. 105), к которой по направлению искомого перемещения приложена единичная сила .

Введем обозначения:

изгибающий момент —

работа внешних сил —

—

изгибающий момент —

работа силы —

—

По первому свойству упругих систем справедливы равенства:

Загрузим систему последовательно сначала единичной силой , а затем, не снимая ее, заданными силами . Из равенства энергии и работы после двух нагружений можно найти перемещение.

Работа после первого нагружения ,

после второго нагружения ,

суммарная ,

Изгибающий момент после двух нагружений

Вычисляем

Приравниваем

;

По аналогии можно вывести формулу интеграла Мора для всех случаев нагружения.

5. Частные случаи записи интеграла Мора

При расчете разных упругих систем учитывают соответствующие силовые факторы, поэтому используют разные формы записи интегралов Мора.

1. Для шарнирных стержневых систем:

2. Для плоских балок, рам и кривых брусьев

3. Для пространственных систем

6. Порядок определения перемещений по интегралу Мора

Для определения перемещений надо рассмотреть заданную и единичную системы. При определении линейного перемещения по направлению искомого перемещения прикладывается единичная сила, а при определении угла поворота сечения – единичный момент.

ычерчиваем заданную и вспомогательную системы (рис. 106), разбиваем их на участки. Границы участков в обеих системах должны совпадать. Для двух систем по участкам записываем выражения силовых факторови составляем интегралы Мора, вычислив которые, получим величину искомого перемещения.

Участок :Участок:

;

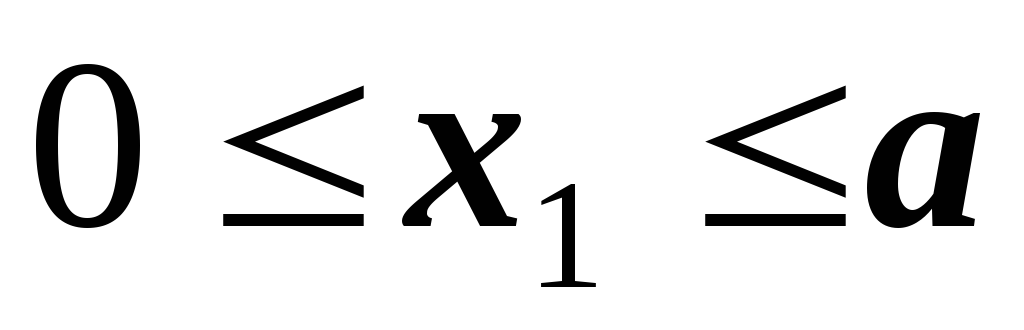
7. Правило Верещагина для вычисления интеграла Мора («перемножение» эпюр)

Интеграл Мора содержит силовые факторы от заданной нагрузки и единичных сил. Метод Верещагина основан на том, что эпюра от единичной силы и момента всегда прямолинейна, никогда не бывает параболы. Жесткость по участкам должна быть постоянной, чтобы ее можно было вынести за знак интеграла.

Вывод проводим на примере эпюр изгибающих моментов (рис. 107), но результат справедлив для любых эпюр, из которых одна линейная.

Постановка задачи: на участке балки с постоянной жесткостьюзаданы эпюрыи. Эпюраимеет произвольное очертание, эпюра— прямая линия без изломов.

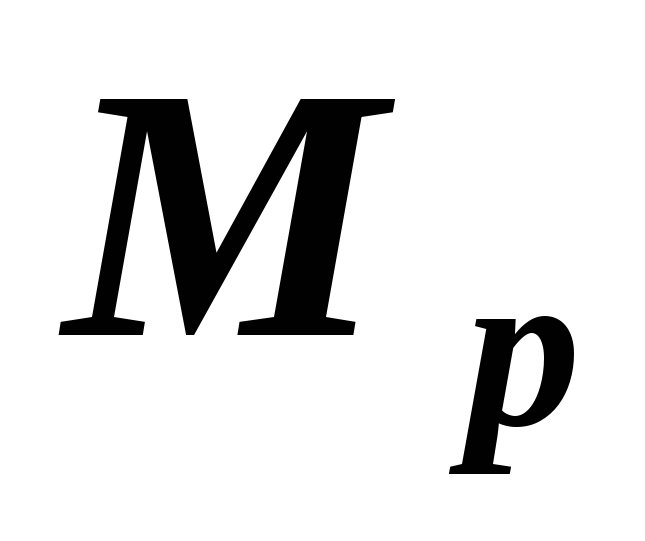
Требуется вычислить интеграл

Получено выражение, позволяющее вычислять интеграл Мора геометрически. Этот способ вычисления называется методом Верещагина.

Правило: Чтобы вычислить интеграл Мора по способу Верещагина нужно построить эпюры подинтегральных функций и, а затем площадь эпюры, обозначаемую, умножить на ординату с эпюрырасположенную под центром тяжести площади, обозначенную —.

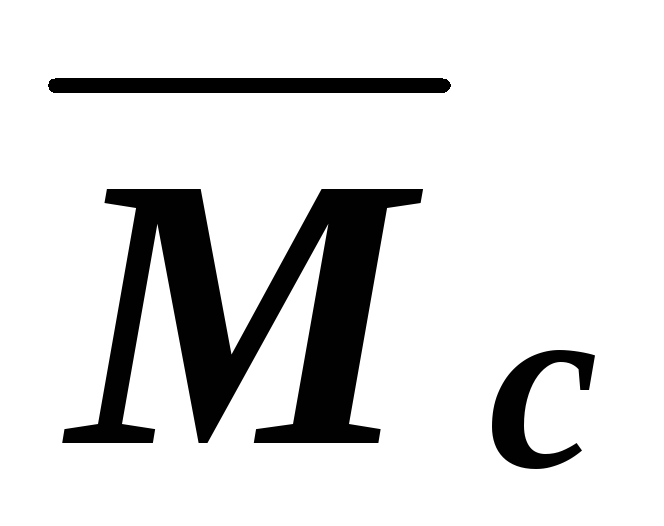
Примечание: Если обе «перемножаемые» эпюры прямолинейные, то, можно, наоборот, площадь брать с эпюры , а ординату с эпюры_.

.

Источник

Определение прогибов и углов поворотов методом Мора

Интеграл Мора позволяет определять прогибы и углы поворота заданного сечения балки, используя интегральное исчисление. Хотя данный метод предпочтительнее метода начальных параметров, он неудобен из-за необходимости вычисления интеграла. Из интеграла Мора был получен удобное для практического применения правило Верещагина, при котором не нужно вычислять интегралы, а только нужно находить площадь и центр тяжести эпюр.

Получение формулы интеграла Мора

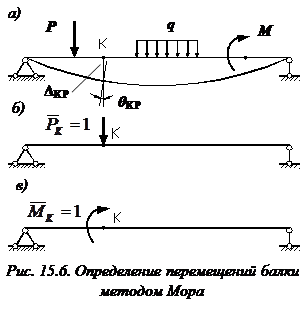
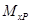
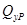
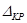
Рассмотрим балку, изображенную на рис. 15.6, а. Обозначим и , соответственно, изгибающий момент и поперечную силу, возникающие в заданной балке от действующей на нее группы нагрузок P. Пусть требуется определить прогиб балки () в точке K.

Введем в рассмотрение вспомогательную балку (та же балка, но нагруженная только единичной силой либо единичным изгибающим моментом). Нагрузим ее только одной силой (рис. 15.6, б). Единичную силу приложим в точке K, где нужно определить прогиб.

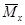
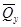
Внутренние усилия, возникающие во вспомогательной балке, обозначим и .

Воспользуемся теперь теоремой о взаимности работ, согласно которой работа внешних сил, приложенных к вспомогательной балке на соответствующих перемещениях заданной балки равна взятой с обратным знаком работе внутренних сил заданной балки на соответствующих перемещениях вспомогательной балки. Тогда .

При определении перемещений в балке, как правило, можно пренебрегать влиянием поперечной силы, ( не учитывать второе слагаемое).

Тогда, учитывая, что , окончательно получим формулу интеграла Мора : .

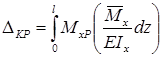
Определение перемещений по формуле интеграла Мора часто называют определением перемещений методом Мора , а саму формулу – интегралом Мора .

Входящие в интеграл Мора изгибающие моменты берутся в произвольном поперечном сечении и поэтому представляют собой аналитические функции от текущей координаты z.

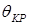
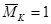
Заметим, что если мы хотим в этой же точке K определить угол поворота поперечного сечения (), то нам необходимо к вспомогательной балке приложить не единичную силу, а единичный момент (рис. 15.6, в).

порядок вычисления перемещений методом Мора:

· к вспомогательной балке в той точке, где требуется определить перемещение, прикладываем единичное усилие. При определении прогиба прикладываем единичную силу , а при определении угла поворота – единичный момент ;

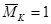
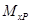
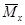
· для каждого участка балки составляем выражения для изгибающих моментов заданной () и вспомогательной () балок;

· вычисляем интеграл Мора для всей балки по соответствующим участкам;

· если вычисленное перемещение имеет положительный знак, то это означает, что его направление совпадает с направлением единичного усилия. Отрицательный знак указывает на то, что действительное направление искомого перемещения противоположно направлению единичного усилия.

Вычисление интеграла Мора пример

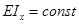
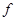
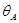
Пусть для шарнирно опертой балки постоянной изгибной жесткости , длиной l, нагруженной равномерно распределенной нагрузкой интенсивностью q (рис. 15.7, а), требуется определить прогиб посредине пролета () и угол поворота на левой опоре ().

определение прогиба с помощью интеграла Мора

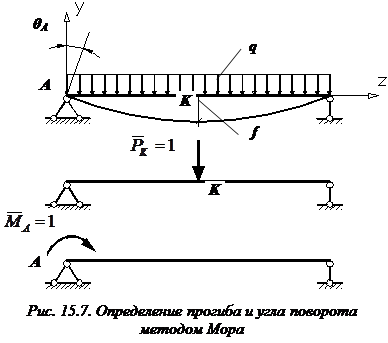
В том месте, где нам нужно определить прогиб, к вспомогательной балке прикладываем единичную силу (рис. 15.7, б).

Записываем выражения для изгибающих моментов для каждого из двух участков () заданной и вспомогательной балок:

.

.

Вычисляем интеграл Мора . Учитывая симметрию балки, получим:

.

Определение угла поворота методом Мора

Нагружаем вспомогательную балку единичным моментом , прикладывая его в том месте, где мы ищем угол поворота (рис. 15.7, в).

Записываем выражения для изгибающих моментов в заданной и вспомогательной балках только для одного участка ():

;

.

Тогда интеграл Мора будет иметь вид:

.

Положительный знак в выражении для угла поворота поперечного сечения балки указывает на то, что поворот сечения происходит по направлению единичного момента .

Источник

4. Интеграл Мора для вычисления перемещений

Вывод формулы проводится для случая плоского изгиба, соответственно учитывается только изгибающий момент . В общем случае нагружения рассуждения аналогичны.

Задана произвольная упругая система, загруженная силами . Требуется определить перемещение произвольной точки в заданном направле-

нии .

Для вывода формулы кроме заданной рассмотрим вспомогательную единичную систему, которая представляет собой заданную упругую систему (рис. 105), к которой по направлению искомого перемещения приложена единичная сила .

Введем обозначения:

изгибающий момент —

работа внешних сил —

—

изгибающий момент —

работа силы —

—

По первому свойству упругих систем справедливы равенства:

Загрузим систему последовательно сначала единичной силой , а затем, не снимая ее, заданными силами . Из равенства энергии и работы после двух нагружений можно найти перемещение.

Работа после первого нагружения ,

после второго нагружения ,

суммарная ,

Изгибающий момент после двух нагружений

Вычисляем

Приравниваем

;

По аналогии можно вывести формулу интеграла Мора для всех случаев нагружения.

5. Частные случаи записи интеграла Мора

При расчете разных упругих систем учитывают соответствующие силовые факторы, поэтому используют разные формы записи интегралов Мора.

1. Для шарнирных стержневых систем:

2. Для плоских балок, рам и кривых брусьев

3. Для пространственных систем

6. Порядок определения перемещений по интегралу Мора

Для определения перемещений надо рассмотреть заданную и единичную системы. При определении линейного перемещения по направлению искомого перемещения прикладывается единичная сила, а при определении угла поворота сечения – единичный момент.

ычерчиваем заданную и вспомогательную системы (рис. 106), разбиваем их на участки. Границы участков в обеих системах должны совпадать. Для двух систем по участкам записываем выражения силовых факторови составляем интегралы Мора, вычислив которые, получим величину искомого перемещения.

Участок :Участок:

;

7. Правило Верещагина для вычисления интеграла Мора («перемножение» эпюр)

Интеграл Мора содержит силовые факторы от заданной нагрузки и единичных сил. Метод Верещагина основан на том, что эпюра от единичной силы и момента всегда прямолинейна, никогда не бывает параболы. Жесткость по участкам должна быть постоянной, чтобы ее можно было вынести за знак интеграла.

Вывод проводим на примере эпюр изгибающих моментов (рис. 107), но результат справедлив для любых эпюр, из которых одна линейная.

Постановка задачи: на участке балки с постоянной жесткостьюзаданы эпюрыи. Эпюраимеет произвольное очертание, эпюра— прямая линия без изломов.

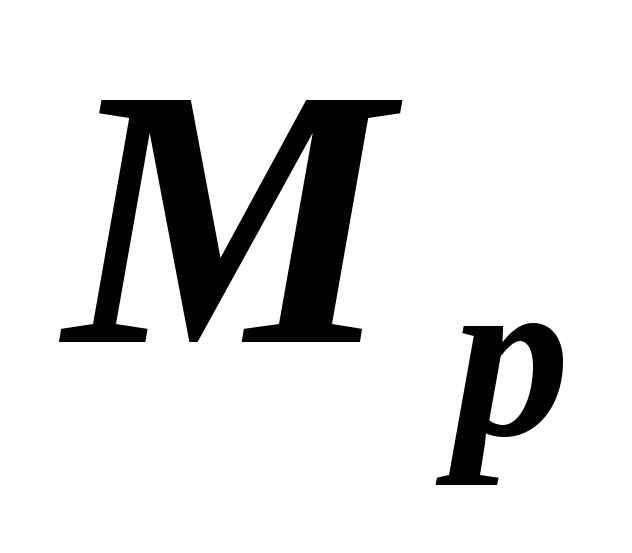
Требуется вычислить интеграл

Получено выражение, позволяющее вычислять интеграл Мора геометрически. Этот способ вычисления называется методом Верещагина.

Правило: Чтобы вычислить интеграл Мора по способу Верещагина нужно построить эпюры подинтегральных функций и, а затем площадь эпюры, обозначаемую, умножить на ординату с эпюрырасположенную под центром тяжести площади, обозначенную —.

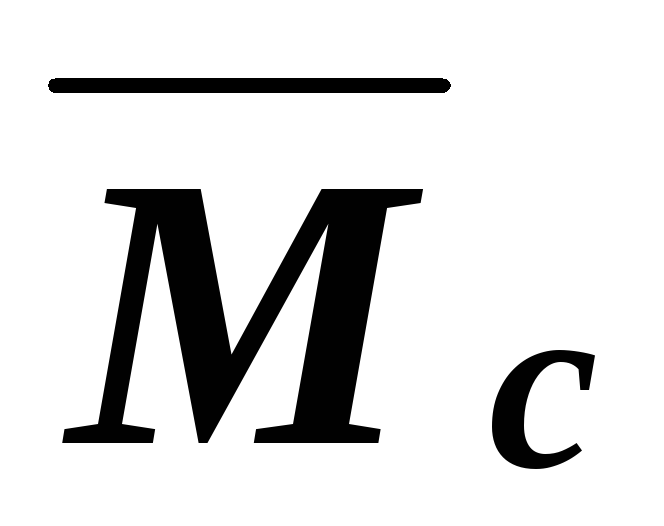
Примечание: Если обе «перемножаемые» эпюры прямолинейные, то, можно, наоборот, площадь брать с эпюры , а ординату с эпюры_.

.

Источник