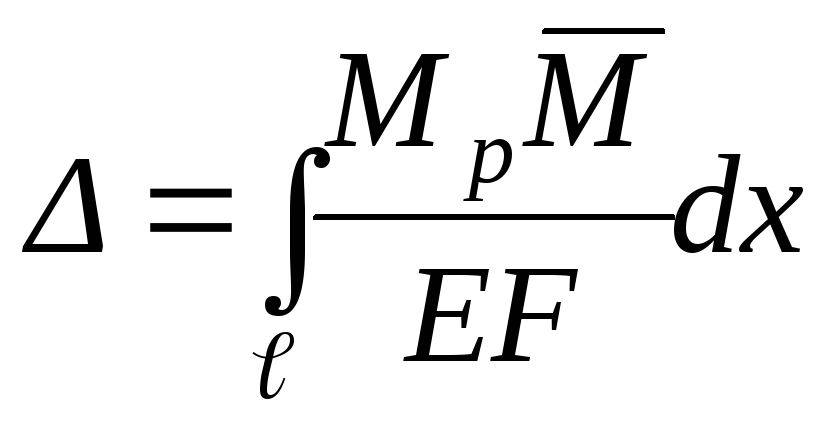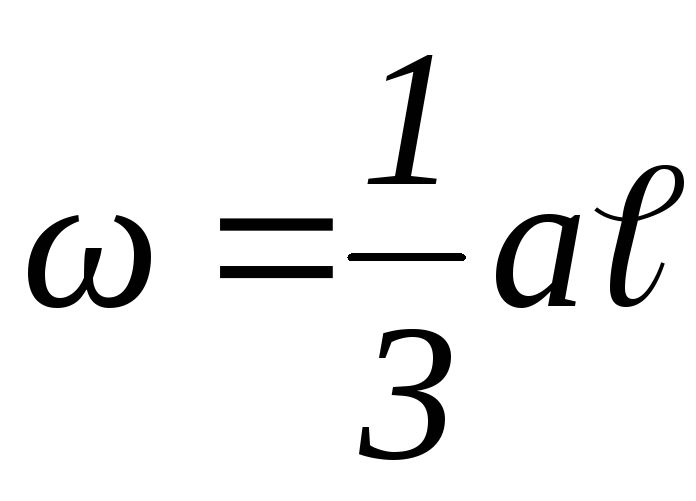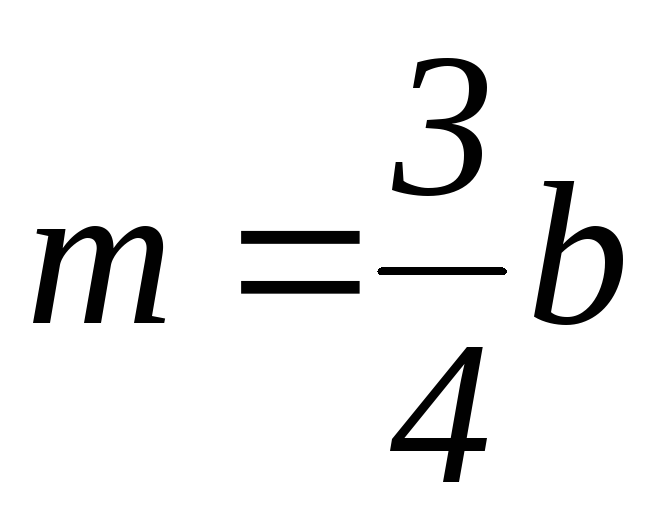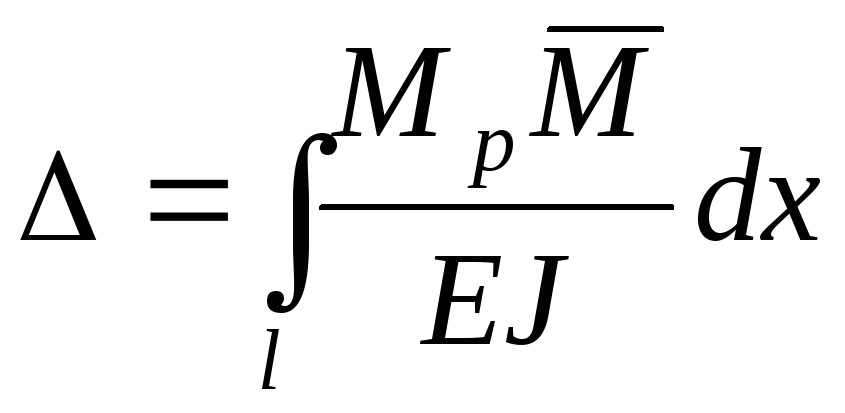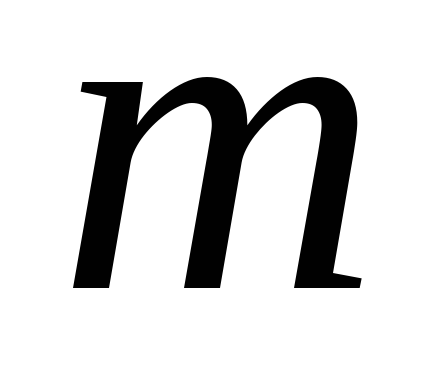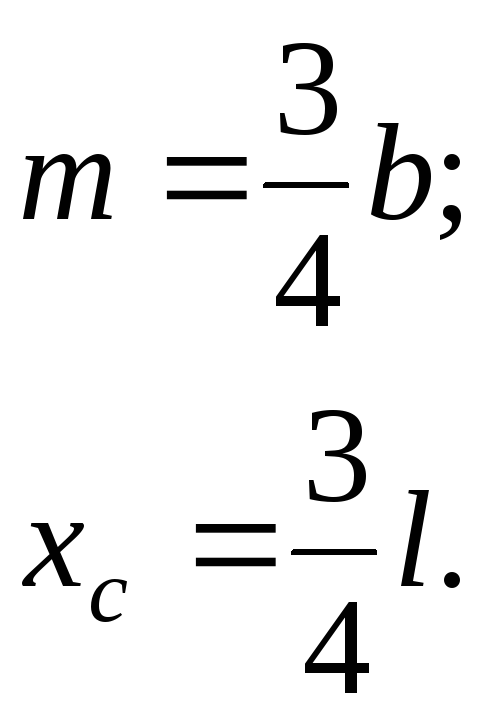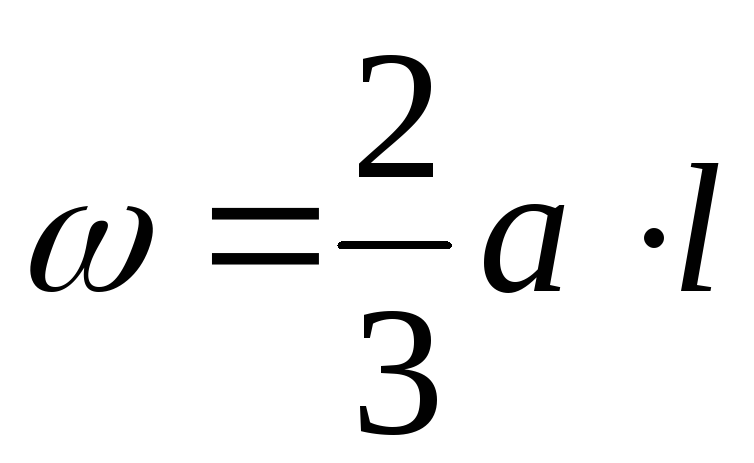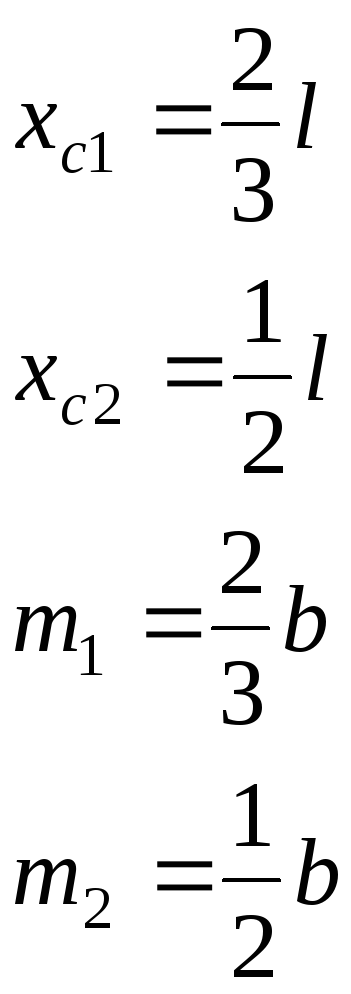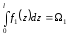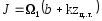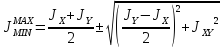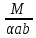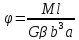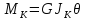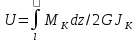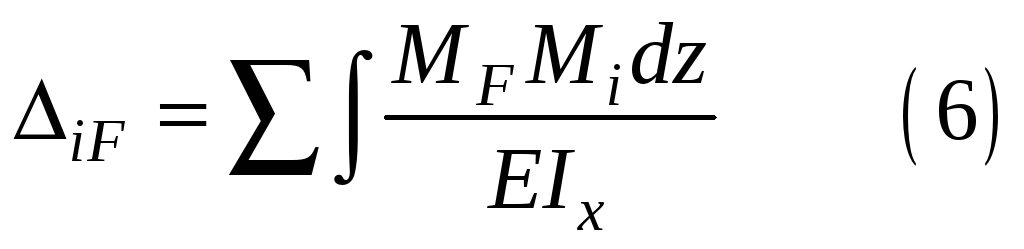Вычисление интегралов мора методом верещагина

1.6. Графический способ вычисления интеграла Мора – способ Верещагина

Упрощение операции интегрирования основано на том, что эпюры от единичных усилий на прямолинейных участках оказываются линейными. Рассмотрим эту процедуру применительно к участку балки. На рис.1.16 сверху показан участок балки с эпюрой М_робщего вида, а внизу эпюра, представляющая линейную функцию. Преобразуем интеграл Мора

(а)

с учётом этой особенности. Как видно из верхнего чертежа, М_рdx = dω, а из нижнего чертежа имеем. Если кроме того считать, что жёсткостьEIна протяжении участка постоянна, вместо (а) будем иметь

. (б)

Интеграл представляет собой статический момент площади эпюрыМ_ротносительно осиу. Его можно записать иначе

S_y = ω ∙ x_c ,

где ω– площадь этой эпюрыМ_р;

х_с– координата центра тяжести эпюрыМ_р.

Отметив на нижней эпюре соответствующую ординату и обозначив её буквой m, будем иметь

x_ctg α = m.

В результате подстановки этих выражений в (б) получим

. (в)

Если балка имеет несколько участков по длине, формула Верещагина будет иметь вид

, (1.27)

где ∆ – обобщённое перемещение (либо прогиб υ, либо угол поворота θ);

ω_i– площадь эпюры моментов от внешней нагрузки (грузовой эпюры);

m_i– ордината единичной эпюры под центром тяжести грузовой эпюры;

n– число участков по длине балки.

При пользовании этой формулой надо уметь вычислять площади и координаты центров тяжести основных фигур: прямоугольника, прямолинейного треугольника и криволинейного треугольника. Минимально необходимые справочные данные приведены в табл.1.1. Процедуру графического вычисления называют «перемножением» эпюр.

В случае, если эпюра М_ртоже линейная, операция перемножения обладает свойством коммутативности: безразлично, умножается ли площадь грузовой эпюры на ординату единичной или площадь единичной на ординату грузовой.

Встречающиеся на практике эпюры могут быть, как правило, разбиты на простые фигуры, приведённые в табл.1.1.

Эпюры М_ри

Примечание: параболы – квадратные.

В качестве примера рассмотрим уже рассчитанную балку на рис.1.13. Чтобы построить эпюры М_р и , можно не определять опорные реакции: достаточно сосчитать момент на опореВ от нагрузки на консоли, построить эпюру на консоли, а затем соединить прямой линией значение М на опоре В с нулём на опоре А (рис.1.17).

В соответствии с формулой (1.27)

.

Конечно, результат получился такой же, что и при интегрировании по формуле Мора, но с меньшими затратами труда.

Глава 2. Статически неопределимые балки

2.1. Общие понятия

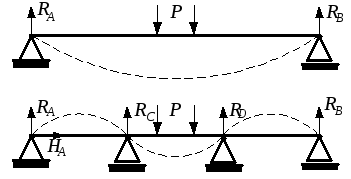
Изложенные в предыдущей главе методы определения перемещений широко применяются в расчётах статически неопределимых балок. Если при проектировании длинных балок (мостов, валов турбин) условия прочности и (или) жёсткости не выполняются, можно увеличить сечение балки, а можно поставить дополнительные опоры в пролёте (рис.2.1,б). Второй путь очень часто оказывается предпочтительным, так как позволяет, не увеличивая вес конструкции, сделать её более жёсткой.

Балка с промежуточными опорами становится статически неопределимой, так как трёх уравнений статики уже недостаточно для определения пяти неизвестных реакций.

Напомним, что простую статически неопределимую систему, образованную из стержней, работающих на растяжение-сжатие, мы рассматривали в разделе 2.5 первой части курса. Дополнительное уравнение для определения продольных сил в стержнях – уравнение совместности деформаций – было получено из рассмотрения схемы деформирования системы. Аналогичным по существу методом рассчитываются статически неопределимые балки.

Степень статической неопределимости определяется числом «лишних» связей. Балка на рис.2.1,б имеет две «лишних» промежуточных опоры – их можно удалить без ущерба для равновесия. Степень статической неопределимости этой балки равна двум.

Источник

2. Правило Мора-Верещагина (графический способ вычисления интеграла Мора)

Кроме метода начальных параметров существует эффективный универсальный метод определения перемещений в балках, рамах и упругих конструкциях произвольной конфигурации – метод Мора. Упругое перемещение (либо прогиб, либо угол поворота сечения) определяется по формуле:

, (1.3)

где – изгибающий момент от заданной нагрузки;– изгибающий момент от единичной силы, приложенной в той точке, в которой определяется перемещение.

Упрощение операций интегрирования возможно для конструкций с прямолинейной осью постоянной жесткости и основано на том, что эпюры от единичных усилий на прямолинейных участках оказываются линейными. Рассматривая эту процедуру применительно к участку балки, преобразуем интеграл Мора с учетом этой особенности. На рис. 1.3 сверху показан участок балки с эпюрой общего вида, а внизу эпюра , представляющая собой линейную функцию. В результате несложного расчета (подробности смотри в учебнике) установлено, что интеграл произведения двух функций и численно равен площади эпюры , умноженной на величину момента, взятого с эпюры в сечении, соответствующем центру тяжести эпюры .

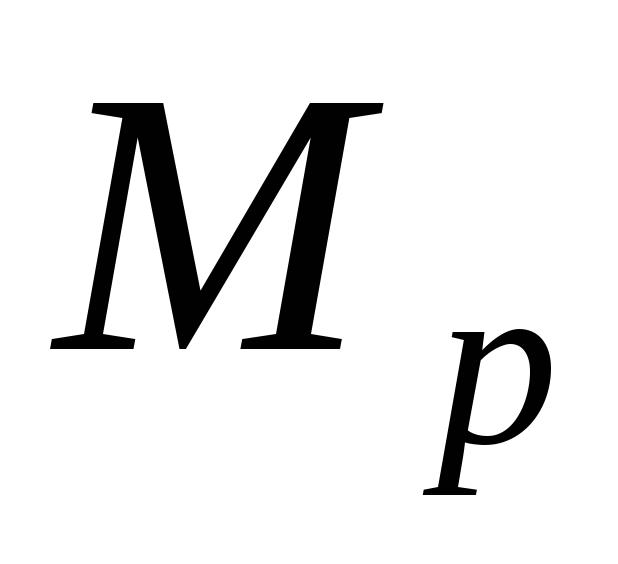
. (1.4)

Если балка имеет несколько участков по длине, формула Верещагина будет иметь вид

, (1.5)

где – площадь эпюры моментов от внешней нагрузки (грузовой эпюры); – ордината единичной эпюры под центром тяжести грузовой эпюры; – число участков по длине балки.

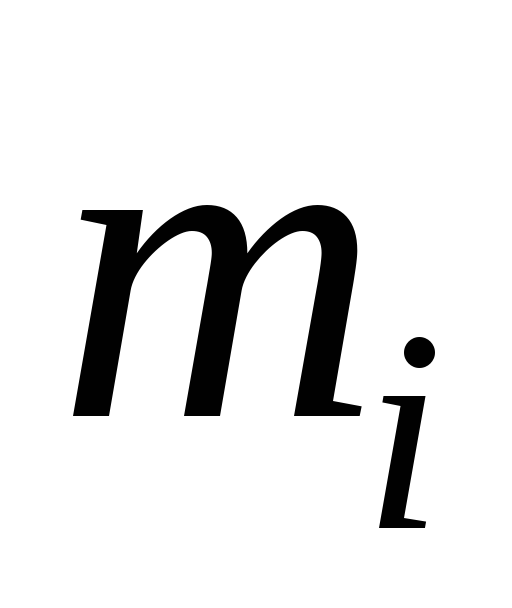
При пользовании этой формулой надо уметь вычислять площади и координаты центров тяжести основных фигур: прямоугольника, прямолинейного треугольника и криволинейного треугольника. Минимально необходимые справочные данные приведены в табл. 1.1. Процедуру графического вычисления называют «перемножением» эпюр.

Эпюры и

эпюры ,

тяжести

Эпюры и

эпюры ,

тяжести

Примечания: 1. Все кривые в табл. 1.1 – квадратные параболы. 2. При «перемножении» эпюр одного знака их произведение положительно. 3. При «перемножении» эпюр разных знаков их произведение отрицательно.

В случае, если эпюра тоже линейная, операция перемножения обладает свойством коммутативности: безразлично, умножается ли площадь грузовой эпюры на ординату единичной или площадь единичной на ординату грузовой.

Рассмотрим на примере расчетной схемы, показанной на рис. 1.4, порядок решения задач при определении перемещения с помощью правила Мора-Верещагина. Определим прогиб в точке .

Чтобы построить эпюры и ,можно не определять опорные реакции: достаточно сосчитать момент на опореот нагрузки на консоли, построить эпюру на консоли, а затем соединить прямой линией значениеM на опореB с нулем на опореA.

В соответствии с формулой (1.5)

.

Источник

2)Вывод формулы способа Верещагина для вычисления интеграла Мора.

Если стержень состоит из прямых участков с постоянной в пределах каждого участка жесткостью, эпюры от единич­ных силовых факторов на прямолинейных участках оказыва­ются линейными.

Положим, на участке длиной 1 нужно взять интеграл от произведения двух функцийf₁(z)*f₂(z):J =f₁ (z) f₂(z) dz (1)

при условии, что хотя бы одна из этих функций — ли­нейная. Пусть f₂(Z) =b +kz. Тогда выражение (1) примет видJ =f₁ (z) dz+ kzf₁ (z) dz

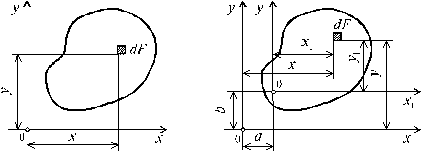
Первый из написанных интегралов представляет собой пло­щадь, ограниченную кривой f₁ (z) (рис. 5.18), или, короче го­воря, площадь эпюрыf₁(z):

Второй интеграл характеризует статический момент этой пло­щади относительно оси ординат, т.е.

где Zц.т — координата центра тяжести первой эпюры. Теперь получаем

Но =f₂(z_ц.т.) Следовательно,

Таким образом, по способу Верещагина операция интегри­рования заменяется перемножением площади первой эпюры на ординату второй (линейной) эпюры под центром тяжести первой.

Билет 20

1)Главные осевые моменты инерции. Определение их величин и направлений главных осей.

Оси, относительно которых центробежный момент J_XcYc=0, наз-ся главными. Осевые моменты инерции относительно главных осей наз-ся главными моментами инерции.

«+» соответсвует максимальному моменту инерции, « — » — минимальному. После того как сечение вычерчено в масштабе и показано положение главных осей на глаз устанавливается направление осей (которой из двух соответствует максимальный, а которой – минимальный момент инерции).

2) Кручение стержня прямоугольного поперечного сечения (определение напряжений и перемещений).

На рисунке показана полученная методом теории упругости эпюра касательных напряжений для бруса прямоугольного сечения. В углах, как мы видим, напряжения равны нулю. Наибольшие напряжения возникают по серединам больших сторон, в точках А:

τ_А= τ_max=

_в=τ_max, где а — большая, b — малая сторона прямоугольника. Коэффициентыизависят от отношения сторонКоэффициент β также зависит от этого отношения. Эти данные приводятся в таблицах.

Угловое перемещение:

Ф-ла для расчёта касательных напряжений: , где

для расчёта углового перемещения:

Для прямоугольника: ,–геометрические параметры, зависящие от формы сечения.

Потенциальная энергия, накопленная закрученным брусом:

Билет 21

1)Определение перемещений при растяжении-сжатии.

, где W – перемещение, – удлинение, N – внутренняя сила на участке, E – модуль упругости первого рода, А – площадь поперечного сечения на участке.

Для однородного стержня длины , при Е= const, N = const:

2) Расчёт на прочность при изгибе. Понятие о расчётном и нормативном коэффициенте запаса.

По принципу независимости действия сил нормаль­ное напряжение в произвольной точке, принадлежащей попереч­ному сечению бруса и имеющей координаты x, y, опр-ся суммой напр-й, обусловленных моментами M_x и M_y , т.е. (5.26)

Mx = Msin; My = Mcos, где- угол между плоскостью главного мемента М и осью Ох или Оу. (5.25)

Правило знаков для моментов: момент считается положительным, если в первой четверти координатной плоскости (там, где координаты x и y обе положительны) он вызывает сжимающие напряжения.

Если изгиб чистый, то один из моментов M_x или M_y равен 0 и выражение (5.26) принимает вид

, где — осевой момент сопротивления,– осевой момент инерции,— расстояние по модулю до наиболее удалённой точки сечения от Ох.

При косом изгибе М_Х , М_{У .}

Уравнение нейтральной линии, т.е. геометрического места точек, где нормальное напряжение принимает нулевые значения, находят, полагая в (5.26)  = 0:

Откуда определяется: (5.27)

Эпюра напряжений в поперечных сечениях бруса линейна, следовательно, максимальные напряжения в сечении возникают в точках наиболее удаленных от нейтральной линии.

Расчёт на прочность при изгибе проводится при условиях:

материал работает одинаково на растяжение и сжатие, т.е.

Условие прочности: , где,, где– допускаемое значение предела текучести,— коэф. запаса.

если неодинаково, то работают два условия:

, где,

Если расчёт проектировочный, то из двух коэффициентов выбирется наибольший. В поверочном – наоборот.

В целях безопасной работы напряжения должны быть ниже предельных значений для данного материала. Таким образом при поверочном расчёте (нахожд. Нормативного коэф. запаса):

, где — предельное кас. напряжение материала,n_Т – коэф. запаса,

за расчётный коэффициент принимают [n] > n_Т, где [n] – нормативный (предписываемый нормами проектирования конструкций) коэф. запаса.

Источник

Метод Мора. Интеграл Мора

Теорема Кастельяно дала нам возможность определять перемещения. Эту теорему используют для отыскания перемещений в пластинках, оболочках. Однако, вычисление потенциальной энергии громоздкая процедура и мы сейчас наметим более простой и наиболее общий путь определения перемещений в стержневых системах.

Пусть задана произвольная стержневая система и нам нужно определить в ней перемещение точки по направлению , вызванное всеми силами системы —

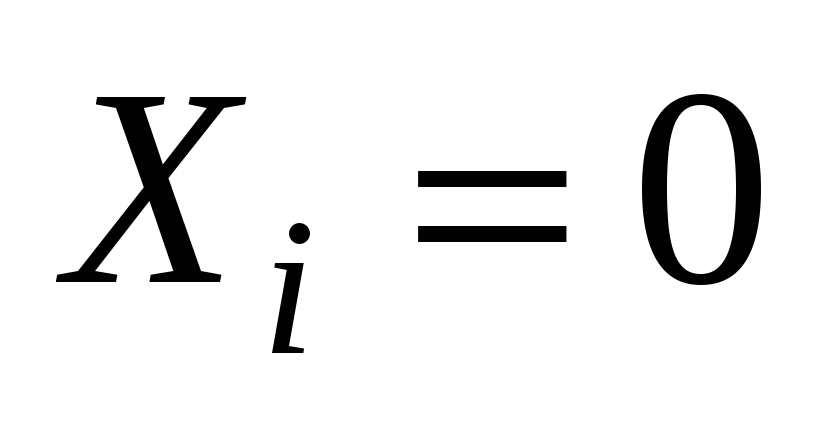
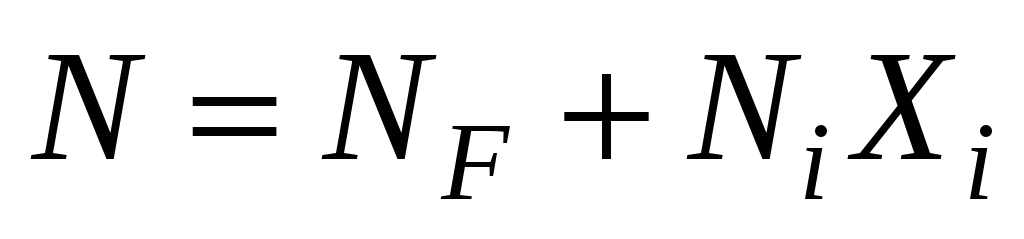
Т.к. в общем случае в системе нет силы, приложенной по направлению искомого перемещения, то воспользоваться теоремой Кастельяно нельзя. Добавим к числу прочих сил силу , приложенную к точке и действующую в направлении . Тогда внутренние силовые факторы в системе можно выразить

, где — внутренние силовые факторы в системе от действующих сил;

— внутренние силовые факторы от силы .

Внесем эти выражения в (3)

По теореме Кастельяно:

Учтя, что

получаем выражение:

называемое интегралом Мора.

Для того, чтобы определить перемещение с помощью метода Мора, необходимо:

1) Определить внутренние силовые факторы в системе от заданных сил.

2) Приложить по направлению искомого перемещения единичную обобщенную силу (единичную силу для определения линейного перемещение, пару сил с моментом равным единице для определения углового перемещения и определить внутренние силовые факторы от единичной силы.

3) Подставить полученные ранее выражения в интеграл Мора и определить перемещение.

Для систем, работающих на изгиб: балок, рам, влияние нормальных сил на величину перемещения незначительно и интеграл Мора в этом случае выглядит:

Источник