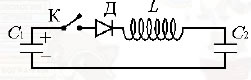2.2. Молекулярная физика и термодинамика
Пример 2.1. (С2). В водонепроницаемый мешок, лежащий на дне моря на глубине 73,1 м, закачивается сверху воздух. Вода вытесняется из мешка через нижнее отверстие, и когда объем воздуха в мешке достигает 28,0 м, мешок всплывает вместе с прикрепленным к нему грузом. Масса оболочки мешка 2710 кг. Определите массу груза. Температура воды равна 7°С, атмосферное давление на уровне моря равно 10 Па. Объемом груза и стенок мешка пренебречь.
В основе решения этой задачи условие, при котором мешок с грузом начнет всплывать: ρVg = Mg + mrg + mвg, где М и mr — масса оболочки мешка и масса груза, V и mв — объем и масса воздуха в мешке, ρ — плотность воды. Следовательно, mr = ρV — М — mв.
Так как мешок заполнен воздухом, то к его состоянию применимо уравнение Менделеева-Клапейрона: pV = RT, где давление воздуха на заданной глубине h можно выразить формулой р = р0+ ρgh, где р0 — атмосферное давление.
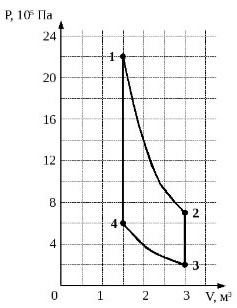
П ример 2.2. (С2). Bo время опыта объем сосуда с воздухом увеличился в 1,5 раза, и воздух перешел из состояния 1 в состояние 2 (см. рисунок). Кран у сосуда был закрыт неплотно, и сквозь него мог просачиваться воздух. Рассчитайте отношение числа молекул газа в сосуде в конце и в начале опыта. Воздух считать идеальным газом.
Основу решения задач этого типа составило уравнение состояния идеального газа в виде р = nkT, где n = — концентрации молекул газа. Отсюда легко получить ответ в общем виде и числовой ответ.
Пример 2.3. С(2). Сосуд разделен пористой перегородкой на две равные части. В начальный момент в одной части сосуда находится 2 моль гелия, а в другой — такое же количество аргона. Атомы гелия могут диффундировать (проникать) через перегородку, а для атомов аргона перегородка непроницаема. Температура гелия равна температуре аргона Т = 300 К. Определите отношение давлений газов на перегородку с разных сторон после установления термодинамического равновесия.
В решении такого рода задач необходимо было рассмотреть состояние системы после установления термодинамического равновесия: в каждой части сосуда окажется по 1 молю гелия. В результате в сосуде с аргоном окажется 3 моля смеси, а с другой стороны перегородки останется 1 моль гелия. Запись уравнения Клапейрона-Менделеева для каждой части сосуда позволит определить давление гелия и смеси: PHeV=RT и PHe+ArV = 3RT, где 2V – объем сосуда. Решение этих уравнений и приведет к ответу на заданный в задаче вопрос.
Пример 2.4. С(2). Цилиндрический сосуд, расположенный горизонтально, разделен тонким поршнем на две равные части. В одной части сосуда находится 1 кг гелия, а в другой — 1 кг аргона. В начальном состоянии поршень удерживается внешними силами. Поршень отпустили, и через некоторое время система пришла в состояние равновесия с окружающей средой, температура которой Т = 300 К. Какую часть цилиндра занимает гелий после установления равновесия? Трением поршня о стенки сосуда пренебречь.
Задача предполагает рассмотрение системы после установления механического и теплового равновесия: давление гелия и аргона на поршень должно быть одинаковым, и температура газов также одинакова рНe= рAr, = р, ТНе = ТAr = Т.
Применение уравнения Клапейрона-Менделеева pVHe = νHeRT, pVAr = νArRT, где νAr=mAr/MAr, νAr, — число молей аргона, a νHe=mHe/MHe — число молей гелия, позволяет получить отношение объемов (учитывая равенство масс газов mНe = mAг = m): = . Но объем сосуда после установления равновесия не изменился VHe + VAr=V, поэтому легко найти искомое отношение = .
Решение следующего цикла задач было основано на понимании школьниками двух тем, вызывающих затруднения уже на уровне обязательного минимума содержания образования – «Первый закон термодинамики» и «Закон сохранения импульса» для случая неупругого соударения, рассмотренных нами выше. Результатом отсутствия понимания смысла этих законов на базовом уровне явилось причиной того, что ни один из участников экзамена не справился с такого рода задачами (пример 2.5).
Пример 2.5. С(6.) В вакууме закреплен горизонтальный цилиндр. В цилиндре находится 1 л гелия, запертого поршнем, при давлении 100 кПа и температуре 300 К. Поршень массой 90 г удерживается упорами и может скользить влево вдоль стенок цилиндра без трения. В поршень попадает пуля массы 10 г, летящая горизонтально, и застревает в нем. Температура гелия в момент остановки поршня в крайнем левом положении возрастает на 90 К. Какова скорость пули? Считать, что за время движения поршня газ не успевает обменяться теплотой с цилиндром и поршнем.
Решение задачи основано на законе сохранения импульса при неупругом соударении: mv0 = (m + M)vn. Отсюда: vn= , где m и М — соответственно масса пули и масса поршня, v0 — скорость пули, vn — скорость поршня после попадания пули.
Формула для расчета внутренней энергии одноатомного идеального газа U = RT, и учет того, что механическая энергия поршня с пулей превращается во внутреннюю энергию гелия, дает возможность рассчитать ΔU: ΔU = RΔT = . Из уравнения Менделеева – Клапейрона следует, что νR = . Решение системы уравнении дает: v0 = .
Источник
Водонепроницаемый мешок лежащий дне моря
30. Парциальное давление водяного пара в комнате возросло, а температура воздуха не изменилась. Как изменилась относительная влажность воздуха? Ответ поясните, указав, какие физические закономерности вы использовали для объяснения. (Решение)
31. В водонепроницаемый мешок, лежащий на дне моря на глубине 73,1 м, закачивается сверху воздух. Вода вытесняется из мешка через нижнее отверстие, и когда объём воздуха в мешке достигает 28,0 м 3 , мешок всплывает вместе с прикреплённым к нему грузом. Масса оболочки мешка 2710 кг. Определите массу груза. Температура воды равна 7 °С, атмосферное давление на уровне моря равно 10 5 Па. Объёмом груза и стенок мешка пренебречь. (Решение)
32. Теплоизолированный сосуд объемом V = 2 м 3 разделен теплоизолирующей перегородкой на две равные части. В одной части сосуда находится 2 моль гелия, а в другой — такое же количество молей аргона. Начальная температура гелия равна 300 К, а температура аргона 600 К. Определите давление смеси после удаления перегородки. Теплоемкостью сосуда пренебречь. (Решение)
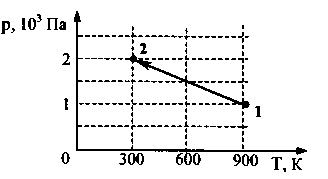
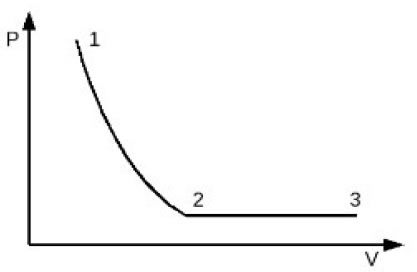
33. Идеальный одноатомный газ в количестве 1 моль сначала изотермически расширился при температуре T1 = 300 К. Затем газ иобарнонагрели, повысив температуру в 3 раза. Какое олчество теплоты олучил газ н участке 2-3? (Решение)
34. В закрытом сосуде находится одноатомный идеальный газ, масса которого 12 г. Вначале давление в сосуде было равно 4·10 5 Па при температуре 400 К. После охлаждения газа давление понизилось до 2·10 5 Па. Какова молярная масса газа, если отданное им количество теплоты равно 7,5 кДж? (Решение)
35. Идеальный одноатомный газ используется в качестве рабочего тела в тепловом двигателе. В ходе работы двигателя состояние газа изменяется в соответствии с циклом, состоящим из двух адиабат и двух изохор (см. рисунок). Вычислите КПД такого двигателя. (Решение)
Источник
Водонепроницаемый мешок лежащий дне моря
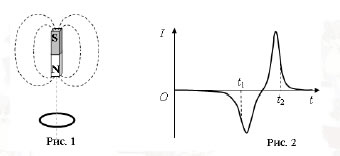
24. Намагниченный стальной стержень начинает свободное падение с нулевой начальной скоростью из положения, изображённого на рис. 1. Пролетая сквозь закреплённое проволочное кольцо, стержень создаёт в нём электрический ток, сила которого изменяется со временем так, как показано на рис. 2.
Почему в моменты времени t1и t2ток в кольце имеет различные направления? Ответ поясните, указав, какие физические явления и закономерности Вы использовали для объяснения. Влиянием тока в кольце на движение магнита пренебречь. (Решение)
25. Небольшой камень, брошенный с ровной горизонтальной поверхности земли под углом к горизонту, упал обратно на землю в 20 метрах от места броска. Сколько времени прошло от броска до того момента, когда его скорость была направлена горизонтально и равна 10 м/с? (Решение).
26. Напряжение на концах первичной обмотки трансформатора 220 В, сила тока в ней 1 А. Напряжение на концах вторичной обмотки 22 В. Какой была бы сила тока во вторичной обмотке при коэффициенте полезного действия трансформатора 95 %? (Решение).
27. В водонепроницаемый мешок, лежащий на дне моря на глубине 73,1 м закачивается сверху воздух. Вода вытесняется из мешка через нижнее отверстие, и когда объём воздуха в мешке достигает 28,0 м3, мешок всплывает вместе с прикреплённым к нему грузом. Масса оболочки 2710 кг. Опреде-лите массу груза. Температура воды равна 7°С. Атмосферное давление на уровне моря равно 10 5 Па. Объёмом груза и стенок мешка пренебречь. (Решение)
28. К конденсатору С1 через диод и катушку индуктивности L подключён конденсатор ёмкостью С2 = 2 мкФ. До замыкания ключа К конденсатор С1 был заряжен до напряжения U = 50 В, а конденсатор С2 не заряжен. После замыкания ключа система перешла в новое состояние равновесия, в котором напряжение на конденсаторе С2 оказалось равным U2 = 20 В. Какова ёмкость конденсатора С1? (Активное сопротивление цепи пренебрежимо мало.) (Решение)
29. На поверхности воды плавает надувной плот шириной 4 м и длиной б м. Небо затянуто сплошным облачным покровом, полностью рассеивающим солнечный свет. На какой максимальной глубине под плотом должна находиться маленькая рыбка, чтобы ее не увидели плавающие вокруг плота хищники? Глубиной погружения плота, рассеиванием света водой и его отражением от дна водоема пренебречь. Показатель преломления воды относительно воздуха принять равным 4/3. (Решение)
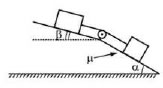
30. В изображенной на рисунке системе нижний брусок может двигаться по наклонной плоскости, составляющей с горизонтом угол α = 30°, а верхний брусок — вдоль наклонной плоскости, составляющей с горизонтом некоторый угол β. Коэффициент трения между нижним бруском и плоскостью равен μ = 0,2, трение между верхним бруском и наклонной плоскостью отсутствует. Считая соединяющую бруски нить очень легкой и нерастяжимой, и пренебрегая массой блока и трением в его оси найдите, при каких значениях угла β нить будет натянута. (Решение)
Источник