1.8 Критерий Кулона-Мора
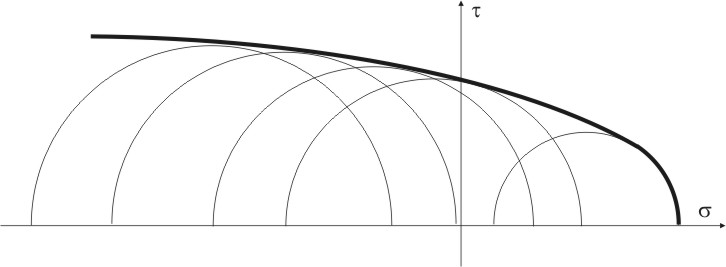
Рассмотренные критерии пластичности применимы для материалов одинаково сопротивляющихся растяжению и сжатию. Однако, ряд материалов обладает разной прочностью при растяжении и сжатии. Критерий Кулона-Мора основан на предположении, что прочность зависит, главным образом, от величины и знака наибольшего 1 и наименьшего3 главных напряжений. Если при некоторых 1 и 3 возникает текучесть, то круг Мора, построенный на этих напряжениях, соответствует предельному состоянию материала. Меняя соотношение между 1 и 3, получим семейство предельных кругов. Огибающая этих кругов определяет сочетания нормальных и касательных напряжений, при которых возникает текучесть материала (рис 9.4).
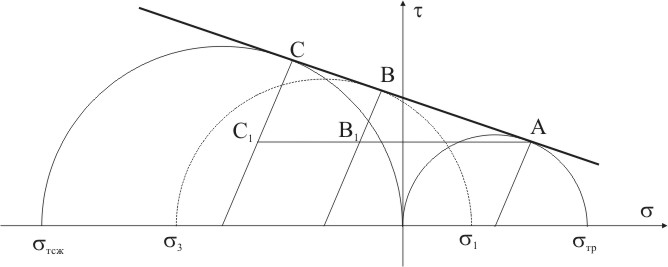
Для точного построения огибающей необходимо выполнить большое количество экспериментов при различных напряженных состояниях. На практике ограничиваются минимальным количеством испытаний для наиболее просто реализуемых напряженных состояний. Огибающую можно с достаточной степенью точностью заменить прямой касательной к кругам Мора построенным для растяжения с диаметром равным пределу текучести при растяжении т р и для сжатия — с диаметром равным пределу текучести при сжатии т сж. Следовательно, для построения схематизированной огибающей достаточно провести испытания образцов материала при одноосном растяжении и при одноосном сжатии. С достаточной степенью точности огибающая заменяется касательной к кругам Мора, соответствующих результатам этих испытаний (рис. 9.5).
Это позволяет найти зависимость между главными напряжениями рассматриваемого напряженного состояния 1 и 3 и эквивалентным напряжением экв при равноопасном одноосном растяжении. В точка касания огибающей с тремя кругами восстановим перпендикуляры, которые совпадают с радиусами кругов, а через точку А проведем горизонтальную прямую. Из подобия треугольников ABB1 и ACC1, следует
Подставим эти выражения в соотношение (1) и после преобразований получим условие тукучести:
Обозначим , тогда условие текучести принимает вид:
Следовательно, эквивалентное напряжение:
При двухосном напряженном состоянии σ3 = 0, следовательно, условие текучести принимает вид:
Учитывая, что для бруса в опасном сечении действуют нормальные напряжения σ и касательные напряжения τmax, тогда главные напряжения:
Подставим выражение (3) в соотношение (2) после преобразований получим условие текучести для бруса:
Эквивалентное напряжение для бруса:
1.9 Условия текучести при двухосном напряженном состоянии
Проанализируем условия текучести при различных критериях для двуосного напряженного состояния. Условия текучести имеют следующий вид:
а) по критерию максимального главного напряжения:
б) по критерию максимальной главной деформации:
в) по критерию суммарной энергии деформации:
σ1 2 + σ2 2 + 2μσ1σ2 = σтр 2
г) по критерию максимальных касательных напряжений:
д) по критериям энергии деформации сдвига и интенсивности напряжений:
Представим эти соотношения в прямоугольных координатах «u-v», которые повернуты относительно координат «σ1-σ2» на 45 против часовой стрелки. Для этого подставим в условия текучести:
Тогда при различных критериях для двуосного напряженного состояния и при равенстве пределов текучести на растяжение и сжатие (σтр = σтсж = σт) условия текучести принимают вид.
а) по критерию максимального главного напряжения:
б) по критерию максимальной главной деформации:
в) по критерию суммарной энергии деформации:
Это уравнение эллипса с центром в начале координат, малой полуосью и большой полуосью ;
г) по критерию максимальных касательных напряжений:
д) по критерию энергии деформации сдвига и интенсивности напряжений:
Это уравнение эллипса с центром в начале координат, малой полуосью и большой полуосью .
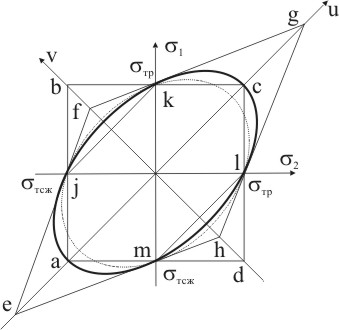
Построим приведенные соотношения в прямоугольных координатах «σ1-σ2» (рис. 9.6).
Фигура Критерий статической прочности
abcd Критерий максимального главного напряжения
efgh Критерий максимальной главной деформации
ajkclm Критерий максимальных касательных напряжений
эллипс (сплошная линия) Критерий энергии деформации сдвигу
эллипс (пунктирная линия) Критерий суммарной энергии деформации
Каждая из фигур означает, что для соответствующего критерия текучесть не наступит до тех пор, пока точка со значениями σ1, σ2 не выйдет за пределы области ограниченной фигурой. Сравнение областей ограниченных различными фигурами показывает, что наименьшая область ограничена шестиугольником ajkclm, который соответствует критерию максимальных касательных напряжений. Можно заметить, что в том случае, когда главные напряжения σ1, и σ2 одновременно растягивающие или сжимающие, то области ограниченные шестиугольником ajkclm и квадратом abcd ( 1-ая и 3-ая четверти прямоугольной системы координат) совпадают. В том случае, когда одно из главных напряжений растягивающее, а другое сжимающее, то область, ограниченная шестиугольником ajkclm меньше области ограниченной квадратом abcd. Это означает, что при прогнозе текучести по критерию максимальных касательных напряжений текучесть наступит раньше, чем по критерию наибольших главных напряжений. Эллипс, ограничивающий область соответствующую, как критерию энергии деформации сдвига, так и критерию интенсивности напряжений огибает шестигранник, соответствующий критерию наибольших касательных напряжений. Таким образом, по критерию энергии деформации сдвига текучесть наступит при больших значениях главных напряжений σ1, и σ2, чем по критерию наибольших касательных напряжений. По критерию максимальной главной деформации область ограничена ромбом диагонали которого совпадают с осями координат u-v, развернутыми относительно исходной системы координат σ1-σ2 на 45.
В заключении следует отметить, что прогноз текучести по шести рассмотренным критериям предельного состояния только по трем критериям (критерий наибольших касательных напряжений, критерий энергии сдвига и критерий интенсивности напряжений) согласуются с результатами эксперимента. Кроме того только эти три критерия позволяют утверждать, что текучесть не наступит при всестороннем растяжении или сжатии в условиях отсутствия касательных напряжений, что также подтверждается экспериментом.
Источник
Расчеты грунтов по модели Кулона-Мора
В качестве критерия прочности для оползней скольжения (как в скальных так и в дисперсных грунтах) наиболее часто используется зависимость Мора-Кулона:
где τ — прочность на сдвиг; u – поровое давление; σ – эффективное нормальные напряжения; φ’ – эффективный угол внутреннего трения; с – сцепление.
Графическое представление зависимости Мора-Кулона приведено на рис. 1.
Рис. 1. Графическое представление зависимости Мора-Кулона
Условие Мора-кулона может быть использовано как в полных, так и в эффективных напряжениях. В терминах полных напряжений, критерий Мора-кулона приобретает следующую простую форму:
где t — прочность на сдвиг; s – полное нормальные напряжения; j – угол внутреннего трения; с – сцепление.
Необходимыми свойствами грунтов для расчета устойчивости склона на основе критерия прочности Мора-Кулона являются сцепление и угол внутреннего трения. Они не используются в решении, при расчете напряжений и деформаций, но необходимы для расчета зон пластического течения, в которых значения напряжений превысили критические значения и закон Гука не выполняется. Использование критерия прочности Мора-Кулона позволяет сравнить расчетное напряжение при сдвиге с теоретическими предельными значениями напряжений.
Однако, при решении практических задач, перечень необходимых свойств грунтов для оценки устойчивости склонов, существенно расширяется. В зависимости от постановки задачи в полных или эффективных напряжениях, определение прочностных характеристик грунта должно выполняться по недренируемой схеме, или по схеме консолидируемых дренированных испытаний. При оценки устойчивости оползневых склонов (в условиях протекания оползневого процесса) в зоне скольжения должны использоваться остаточные параметры прочности грунтов, при оценке потенциальной оползневой опасности склона (в случае отсутствия оползневого процесса на исследуемом склоне) – должны использоваться пиковые параметры прочности грунтов.
В свою очередь, удельное сцепление грунтов может быть представлено как сумма двух параметров — сс- структурного сцепления и Σw – связанности грунта при заданной влажности.
По Н.Н. Маслову выделяются три типа глинистых грунтов: жёсткие (хрупко-упругие); скрытопластичные (вязкопластичные) и пластичные (вязкотекучие).
К жёстким глинистым грунтам в большинстве случаев относятся грунты до четвертичного возраста. Связанность жестких глинистых грунтов много меньше их структурного сцепления и может быть приравненной к 0, а угол внутреннего трения мало зависит от влажности. Уравнение сопротивления сдвигу для таких грунтов имеет следующий вид:
Прочность на сдвиг скрыто пластичных глинистых грунтов выражается зависимостью:
При этом величины φw и Sw сильно зависят от влажности. В случае нарушения структуры скрытопластичных глинистых грунтов зависимость прочности на сдвиг принимает следующий вид:
Прочность на сдвиг идеально пластичных глинистых грунтов выражается зависимостью:
Как следует из приведенной формулы, в таких грунтах угол внутреннего трения и структурное сцепление принимаются равными 0. В случае нарушения структуры пластичных глинистых грунтов сопротивление прочности на сдвиг в них меняется очень слабо по сравнению с ненарушенной структурой.
В настоящее время существует большое количество модификаций классической зависимости Мора-Кулона. Типичным примером является билинейная модель прочности.
На рис. 1 представлен модифицированный билинейный критерий Мора-Кулона. Огибающая кривая прочности определяется двумя значениями σ (угла внутреннего трения) и удельного сцепления, а также нормальным напряжением в плоскости сдвига, при котором наступает состояние текучести.
Рис. 1. Билинейная модель огибающей кривой сдвига.
Согласно данной модели, в том случае, если нормальное напряжение в плоскости сдвига больше заданного значения, в критерии прочности Мора-Кулона используются значения угла внутреннего трения и сцепления Phi2 и С(computed) соответственно. Билинейная модель прочности была первой попыткой учесть нелинейность в критерии Мора-Кулона.
Типичным примером билинейной модели прочности Мора-Кулона является критерий Паттона (Patton FD (1966). Multiple modes of shear failure in rock. Proceedings of 1st Congress of International Society of Rock Mechanics, Lisbon, 1, 509–513.), разработанный для скальных грунтов и учитывающий эффект шероховатости трещин:
Где φb – базовый угол внутреннего трения породы, i – угол шероховатости, σn – эффективное напряжение, σny — эффективное нормальное напряжение, вызывающее проскальзывание микродефектов шероховатости, сjed – эквивалентное сцепление (прочность на сдвиг за счет зацепления микродефектов).
Данная разновидность модели прочности Мора-Кулона, в последние годы так же нашла широкое применение при оценке устойчивости различных нестационарных состояний оползневых (потенциально оползнеопасных) склонов, таких как падение Ку при быстрой сработке уровня подземных вод или при по этапном псевдостатическом анализе учета сейсмического воздействия (Дункан и Райт).
Модель Кулона-Мора пожалуй самая распространенная модель используемая в геотехнических расчетах. С момента создания данной функции прошло уже несколько столетий, при этом модель не только не потеряла своей актуальности, но и постоянно используется в создании новых аналитических выражений. В инженерно-строительной практике данная модель внедренна в различные методики. С ее помощью рассчитывают основания и фундаменты по двум предельным состояниям.
Источник
Построение паспорта прочности согласно условию прочности Кулона-Мора
Критерий прочности Кулона-Мора является самым распространенным критерием и применяется, как для описания грунтов, так и горных пород. Хотя данный критерий не разрабатывался специально для описания трещиноватых горных пород, он может быть применен в тех случаях, когда нет возможности получить достоверные данные для выбора других критериев прочности, а также для описания поведения скальных пород со значительной степенью трещиноватости, путем ввода коэффициента структурного ослабления.
Условие прочности Кулона-Мора в осях нормальных 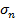
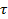
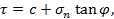 | (1.1) |
а в осях главных нормальных напряжений как
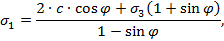 | (1.2) |
где 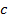
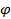


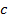
Прочность на одноосное сжатие можно определить по следующей зависимости
 | (1.3) |
на одноосное растяжение
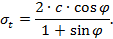 | (1.4) |
При построении паспорта прочности горной породы горной породы воспользуемся
Источник