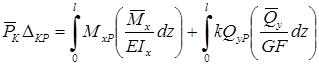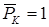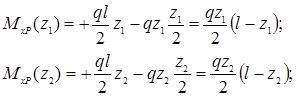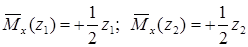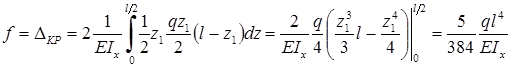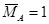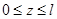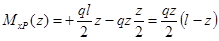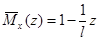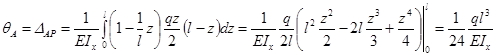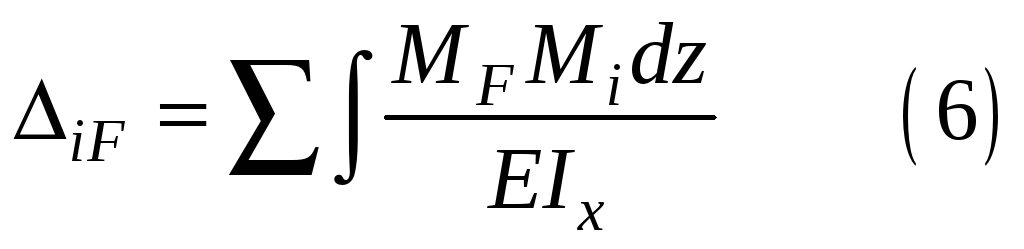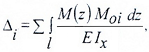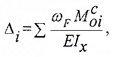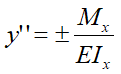Угловое перемещение интеграл мора

1.2 Порядок выполнения расчета углового перемещения сечения «д» балки с помощью интеграла Мора

Расчет ведется в том же порядке, что и при вычислении прогиба. Однако вместо единичной силы в сечении, где необходимо найти угловое перемещение (в данной задаче – в сечении «Д»), прикладывается безразмерный единичный момент = 1. Дальнейшее вычисление углового перемещения _Д (угла поворота сечения «Д») производится в соответствии с п.п. 1.1.8, 1.1.9, 1.1.10.

1.3 Порядок выполнения расчета вертикального перемещения сечения «д» рамы с помощью формулы Симпсона

1.3.1 В соответствии с индивидуальным шифром:

— выписать исходные данные из таблицы 1.1 (номер расчетной схемы, нагрузки F, M, q, размеры h и l);

— начертить заданную расчетную схему рамы (рисунок 1.2).

1.3.2 Вычислить реакции опор от внешних нагрузок (см. «Методические указания…», часть 1, раздел 2 – вычисление ВСФ).

1.3.3 Вычислить значения продольной силы, поперечной силы и изгибающего момента (N_z, Q_у и M_х) от внешних нагрузок и построить их эпюры.

1.3.4 Из условия прочности при изгибе вычислить осевой момент сопротивления сечения балки W_x

где — максимальный изгибающий момент (принимается максимальная

абсолютная величина из эпюры М_х).

1.3.5 По сортаменту прокатных сечений (ГОСТ 8239-89, приложение В, таблица В.2), зная величину W_x:

— подобрать двутавровое сечение стандартного профиля (номер двутавра);

— выписать из таблицы сортамента значение главного момента инерции J_х (см 4 ) выбранного двутавра.

1.3.6 Начертить схему данной балки, отбросив все внешние нагрузки.

1.3.7 Приложить вертикальную единичную силу = 1 в точке, где необходимо найти вертикальное перемещение Δ (в данной задаче – в точке Д).

1.3.8 Вычислить реакции опор от единичной вертикальной силы = 1.

1.3.9 Вычислить значения изгибающего момента и построить единичную эпюру .

1.3.10 Вычислить вертикальное перемещение Δ_Д сечения Д по формуле Симпсона

где n – количество участков;

l — длина участка эпюр;

— ординаты левого, среднего и правого изгибающего

момента на соответствующем участке эпюры

— ординаты левого, среднего и правого изгибающего

момента на соответствующем участке эпюры _.

_{Замечание. Положительный ответ при решении означает, что действительное перемещение совпадает с направлением единичной силы.}

_{Отрицательный ответ означает, что действительное перемещение обратно направлению единичной силы.}

1.4 Порядок выполнения расчета углового перемещения сечения «д» рамы с помощью формулы Симпсона

Расчет ведется в том же порядке, что и при вычислении вертикального перемещения, только вместо единичной силы в сечении, где необходимо найти угловое перемещение (в данной задаче – в сечении «Д»), прикладывается безразмерный единичный момент = 1. Дальнейшее вычисление углового перемещения _Д (угла поворота сечения «Д») производится в соответствии с п.п. 1.3.8, 1.3.9, 1.3.10.

Источник

Определение прогибов и углов поворотов методом Мора

Интеграл Мора позволяет определять прогибы и углы поворота заданного сечения балки, используя интегральное исчисление. Хотя данный метод предпочтительнее метода начальных параметров, он неудобен из-за необходимости вычисления интеграла. Из интеграла Мора был получен удобное для практического применения правило Верещагина, при котором не нужно вычислять интегралы, а только нужно находить площадь и центр тяжести эпюр.

Получение формулы интеграла Мора

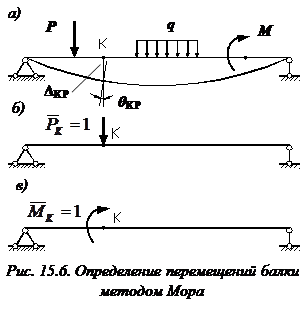
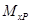
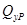
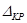
Рассмотрим балку, изображенную на рис. 15.6, а. Обозначим и , соответственно, изгибающий момент и поперечную силу, возникающие в заданной балке от действующей на нее группы нагрузок P. Пусть требуется определить прогиб балки () в точке K.

Введем в рассмотрение вспомогательную балку (та же балка, но нагруженная только единичной силой либо единичным изгибающим моментом). Нагрузим ее только одной силой (рис. 15.6, б). Единичную силу приложим в точке K, где нужно определить прогиб.

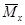
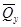
Внутренние усилия, возникающие во вспомогательной балке, обозначим и .

Воспользуемся теперь теоремой о взаимности работ, согласно которой работа внешних сил, приложенных к вспомогательной балке на соответствующих перемещениях заданной балки равна взятой с обратным знаком работе внутренних сил заданной балки на соответствующих перемещениях вспомогательной балки. Тогда .

При определении перемещений в балке, как правило, можно пренебрегать влиянием поперечной силы, ( не учитывать второе слагаемое).

Тогда, учитывая, что , окончательно получим формулу интеграла Мора : .

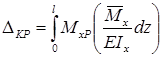
Определение перемещений по формуле интеграла Мора часто называют определением перемещений методом Мора , а саму формулу – интегралом Мора .

Входящие в интеграл Мора изгибающие моменты берутся в произвольном поперечном сечении и поэтому представляют собой аналитические функции от текущей координаты z.

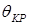
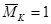
Заметим, что если мы хотим в этой же точке K определить угол поворота поперечного сечения (), то нам необходимо к вспомогательной балке приложить не единичную силу, а единичный момент (рис. 15.6, в).

порядок вычисления перемещений методом Мора:

· к вспомогательной балке в той точке, где требуется определить перемещение, прикладываем единичное усилие. При определении прогиба прикладываем единичную силу , а при определении угла поворота – единичный момент ;

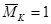
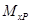
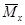
· для каждого участка балки составляем выражения для изгибающих моментов заданной () и вспомогательной () балок;

· вычисляем интеграл Мора для всей балки по соответствующим участкам;

· если вычисленное перемещение имеет положительный знак, то это означает, что его направление совпадает с направлением единичного усилия. Отрицательный знак указывает на то, что действительное направление искомого перемещения противоположно направлению единичного усилия.

Вычисление интеграла Мора пример

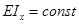
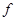
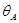
Пусть для шарнирно опертой балки постоянной изгибной жесткости , длиной l, нагруженной равномерно распределенной нагрузкой интенсивностью q (рис. 15.7, а), требуется определить прогиб посредине пролета () и угол поворота на левой опоре ().

определение прогиба с помощью интеграла Мора

В том месте, где нам нужно определить прогиб, к вспомогательной балке прикладываем единичную силу (рис. 15.7, б).

Записываем выражения для изгибающих моментов для каждого из двух участков () заданной и вспомогательной балок:

.

.

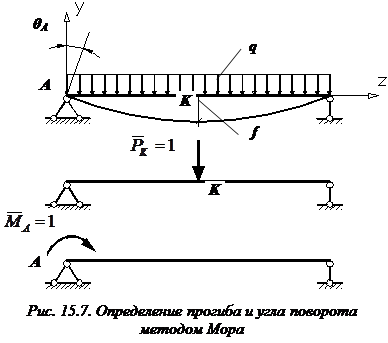
Вычисляем интеграл Мора . Учитывая симметрию балки, получим:

.

Определение угла поворота методом Мора

Нагружаем вспомогательную балку единичным моментом , прикладывая его в том месте, где мы ищем угол поворота (рис. 15.7, в).

Записываем выражения для изгибающих моментов в заданной и вспомогательной балках только для одного участка ():

;

.

Тогда интеграл Мора будет иметь вид:

.

Положительный знак в выражении для угла поворота поперечного сечения балки указывает на то, что поворот сечения происходит по направлению единичного момента .

Источник

Метод Мора. Интеграл Мора

Теорема Кастельяно дала нам возможность определять перемещения. Эту теорему используют для отыскания перемещений в пластинках, оболочках. Однако, вычисление потенциальной энергии громоздкая процедура и мы сейчас наметим более простой и наиболее общий путь определения перемещений в стержневых системах.

Пусть задана произвольная стержневая система и нам нужно определить в ней перемещение точки по направлению , вызванное всеми силами системы —

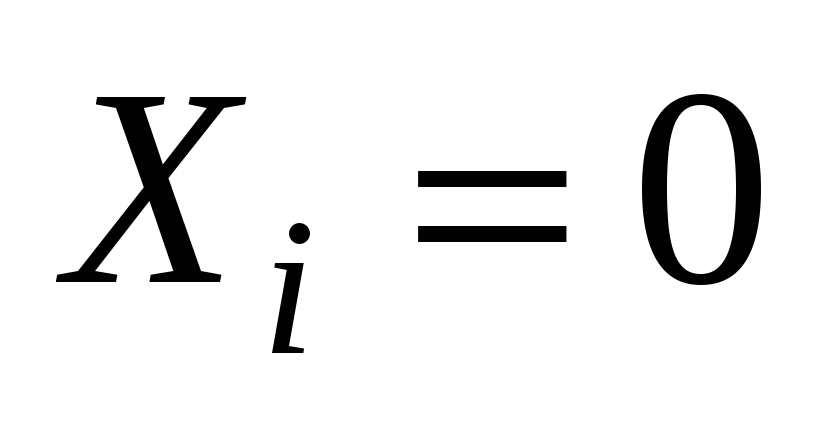
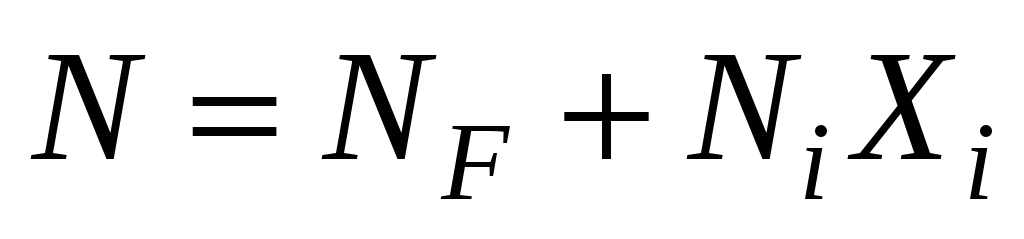
Т.к. в общем случае в системе нет силы, приложенной по направлению искомого перемещения, то воспользоваться теоремой Кастельяно нельзя. Добавим к числу прочих сил силу , приложенную к точке и действующую в направлении . Тогда внутренние силовые факторы в системе можно выразить

, где — внутренние силовые факторы в системе от действующих сил;

— внутренние силовые факторы от силы .

Внесем эти выражения в (3)

По теореме Кастельяно:

Учтя, что

получаем выражение:

называемое интегралом Мора.

Для того, чтобы определить перемещение с помощью метода Мора, необходимо:

1) Определить внутренние силовые факторы в системе от заданных сил.

2) Приложить по направлению искомого перемещения единичную обобщенную силу (единичную силу для определения линейного перемещение, пару сил с моментом равным единице для определения углового перемещения и определить внутренние силовые факторы от единичной силы.

3) Подставить полученные ранее выражения в интеграл Мора и определить перемещение.

Для систем, работающих на изгиб: балок, рам, влияние нормальных сил на величину перемещения незначительно и интеграл Мора в этом случае выглядит:

Источник

Перемещения при изгибе

Как отмечалось ранее, деформацией при изгибе является искривление продольной оси балки.

Вследствие этого искривления, точки и поперечные сечения балки получают линейные и угловые перемещения.

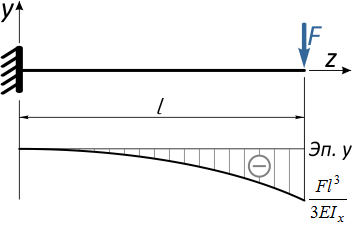
Рассмотрим на примере простой консольной балки.

Линейные перемещения

Отметим в произвольном месте балки точку K и приложим к свободному концу консоли сосредоточенную силу F.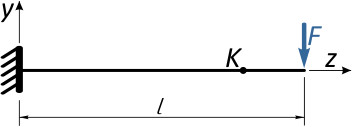

Под действием этой силы балка изогнется, и точка K переместится в новое положение K’.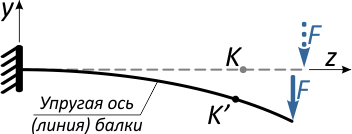

Очевидно, что перемещение точки K произойдет, не строго вертикально, поэтому разложим его на две составляющие:
вертикальное перемещение по оси y, называемое прогибом балки в т. K (y_K)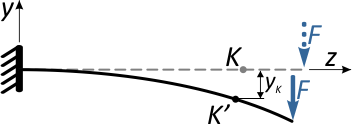

и горизонтальное (осевое) смещение точки вдоль горизонтальной оси — z_K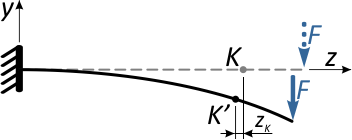

Практические расчеты показывают, что осевые смещения как правило, несоизмеримо меньше вертикальных перемещений (например, в данном случае z_K >

Интеграл Мора

Интеграл Мора относится к энергетическим методам расчета перемещений.

В отличие от МНП позволяет определять линейные и угловые перемещения для любых систем.
Подробнее >>

Способ Верещагина

Данный способ расчета перемещений представляет собой графическую интерпретацию интеграла Мора, особенностью которой является «перемножение эпюр» грузовой и единичных схем.

Подробнее >>

Метод интегрирования дифференциального уравнения упругой линии балки

Непосредственное интегрирование дифференциального уравнения упругой линии

является одним из наиболее универсальных способов расчета перемещений в балках. Может применяться без ограничений к балкам любой формы.

По результатам расчета перемещений сечений балки строится линия изогнутой оси балки (либо эпюра прогибов), с указанием числовых значений прогибов и углов наклона в характерных сечениях.

Эти вычисления и построения необходимы для проверки балок на жесткость.

Источник