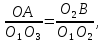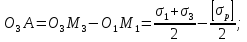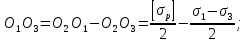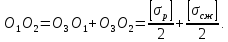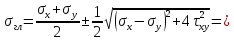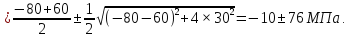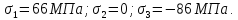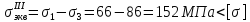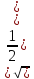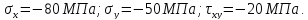Теория разрушения мора вывод

Вся теория для подготовки

PDF-файл из архива «Вся теория для подготовки», который расположен в категории » «. Всё это находится в предмете «сопротивление материалов» из 4 семестр, которые можно найти в файловом архиве МГТУ им. Н.Э.Баумана. Не смотря на прямую связь этого архива с МГТУ им. Н.Э.Баумана, его также можно найти и в других разделах. Архив можно найти в разделе «к экзамену/зачёту», в предмете «сопротивление материалов» в общих файлах.

Просмотр PDF-файла онлайн

Текст из PDF

Экзаменационные вопросыпо второй части общего курса «Сопротивление материалов»1. Расчет статически неопределимых стержневых систем методом сил. Выводканонических уравнений.2. Учет симметрии при расчете статически неопределимых стержневых систем.3. Особенности расчета статически неопределимых многоопорных балок.4. Особенности расчета плоскопространственных рам.5. Расчет балок по предельной нагрузке. Понятие о пластическом шарнире.Определение внутреннего предельного момента для балки с сечением,имеющим одну ось симметрии. (Для бакалавров)6. Определение перемещений в статически неопределимых стержневыхсистемах.7. Методы проверки расчета статически неопределимых стержневых систем.8. Теория напряженного состояния. Определение напряжений в произвольнойплощадке, проходящей через заданную точку. Понятие о тензоре напряжений.9. Теория напряженного состояния. Определение главных напряжений в общемслучае напряженного состояния.10. Вывод формулы определения главных напряжений, в случае если одноглавное напряжение известно.11. Деление тензора напряжений на шаровую и девиаторную составляющие.12. Теория напряжений. Круговая диаграмма О.Мора.13. Теория деформаций. Деформированное состояние в точке. Главныедеформации. Объемная деформация.14. Обобщенный закон Гука для изотропного материала.15. Вывод формулы определения удельной потенциальной энергиидеформации в общем случае напряженного состояния.16. Эквивалентное напряжение. Коэффициент запаса для сложногонапряженного состояния.17. Теория начала текучести наибольших касательных напряжений. Выводформулы определения эквивалентного напряжения.18. Теория начала текучести энергии изменения формы. Вывод формулыопределения эквивалентного напряжения.19. Теория разрушения О.Мора. Вывод формулы для эквивалентногонапряжения.20. Вывод формул для вычисления эквивалентного напряжения в случаеплоского упрощенного напряженного состояния по двум теориям началатекучести и теории разрушения О.Мора.21. Основы механики разрушения. Энергетический критерий роста трещин.22. Основы механики разрушения. Силовой критерий роста трещин.23. Безмоментная теория расчета оболочек вращения. Вывод уравненияЛапласа.24. Определение напряжений в цилиндрической и сферической оболочках,нагруженных равномерным внутренним давлением по безмоментной теории.25. Осесимметричный изгиб круглых пластин. Основные гипотезы. Выводгеометрических соотношений (зависимость деформаций и перемещений отугла поворота нормали). (Для бакалавров)26. Осесимметричный изгиб круглых пластин. Основные гипотезы.Напряженное состояние. Интенсивности сил и моментов. Уравненияравновесия. (Для бакалавров)27. Определение интенсивности поперечных сил при изгибе пластин. Привестипримеры. (Для бакалавров)28. Формулировка граничных условий для определения функции углов поворотанормали и функции прогибов в задаче изгиба пластин. (Для бакалавров)29. Расчет толстостенных труб. Постановка задачи. Вывод дифференциальногоуравнения равновесия элемента трубы.30. Расчет толстостенных труб. Постановка задачи. Условие совместностидеформаций.31. Задача Ламе. Распределение окружных и радиальных напряжений втолстостенной трубе, нагруженной внутренним давлением.32. Задача Ламе. Распределение окружных и радиальных напряжений втолстостенной трубе, нагруженной внешним давлением.33. Определение теоретического коэффициента концентрации напряжений напримере анализа напряжений в равномерно растянутом диске с отверстием.34. Основы расчета составных труб.35. Устойчивость продольно сжатых стержней. Определение основныхпонятий: устойчивость, бифуркация форм равновесия, критическая сила.Примеры потери устойчивости.36. Статический метод (метод Эйлера) решения задач устойчивости стержня.Вывод формулы определения критической силы для шарнирно закрепленногостержня (Задача Эйлера).37. Устойчивость сжатых стержней. Коэффициент приведения длины.Примеры определения коэффициента приведения длины.38. Устойчивость сжатых стержней. Вывод формулы вычисления критическойнагрузки энергетическим методом. Выбор пробной функции прогиба длярешения задачи нахождения критической силы энергетическим методом.39. Пределы применимости формулы Эйлера для вычисления критическихнагрузок. Определение значения гибкости стержня, до которого справедливаформула Эйлера. График зависимости критических напряжений от гибкости.Определение критических напряжений при малой гибкости стержня.40. Расчет на устойчивость по коэффициенту понижения допускаемыхнапряжений.41. Продольно-поперечный изгиб стержня. Использование дифференциальногоуравнения упругой линии для определения прогибов стержня.42. Продольно-поперечный изгиб стержня. Вывод формулы С.П.Тимошенкодля приближенного определения прогибов.43. Расчеты на прочность при циклически изменяющихся напряжениях.Основные понятия об усталости материалов. Характеристики цикла. Криваяусталости и определение предела выносливости.44. Усталостная прочность. Схематизация диаграммы предельных амплитуд.45. Влияние концентрации напряжений на усталостную прочность.46. Влияние качества обработки и состояния поверхностного слоя наусталостную прочность.47. Влияние абсолютных размеров поперечных сечений деталей наусталостную прочность.48. Вывод формулы для определения коэффициента запаса усталостнойпрочности при напряжениях, переменных во времени.49. Определение коэффициента запаса усталостной прочности при совместномизгибе и кручении стержня.50. Расчеты на ударную нагрузку.1. Расчет статически неопределимых стержневых систем методом сил. Вывод канонических уравненийСтатически неопределимые балки и рамы – конструкции, в которых уравненийстатики недостаточно для определения опорных реакций и внутренних усилий. Числосвязей, наложенных на статически неопределимую систему, больше того количествасвязей, которые обеспечивают геометрическую неизменяемость конструкции. Такимисвязями могут быть как опорные связи, так и стержни самой конструкции.Шарнирно-подвижная опора запрещает перемещение по направлению,перпендикулярному плоскости опирания, и является одной связью. Шарнирнонеподвижная опора делает невозможными линейные перемещения по двум взаимноперпендикулярным направлениям (вертикальному и горизонтальному) и соответствуетдвум связям, наложенным на конструкцию. Наконец, при наличии жесткого защемленияна конце стержня становятся невозможными все перемещения: и вертикальное, игоризонтальное, и угол поворота, поэтому жесткое защемление представляет собой трисвязи, обеспечивающие геометрическую неизменяемость балки (рамы). Каждаядополнительнаясвязьсверхтрехдляплоскихсистемпревращаетконструкцию в статически неопределимую. Такие дополнительные связи, которые неявляются необходимыми для обеспечения геометрической неизменяемости конструкции,называются лишними.Статически неопределимые системы обладают рядом характерных особенностей:1. Статически неопределимая система ввиду наличия добавочных лишних связей,по сравнению с соответствующей статически определимой системой оказывается болеежесткой.2. В статически неопределимых системах возникают меньшие внутренние усилия,что определяет их экономичность по сравнению со статически определимыми системамипри одинаковых внешних нагрузках.3. Разрушение лишних связей в нагруженном состоянии, не ведет к разрушениювсей системы в целом, так как удаление этих связей приводит к новой геометрическинеизменяемой системе, в то время как потеря связи в статически определимой системеприводит к изменяемой системе.4. Для расчета статически неопределимых систем необходимо предварительнозадаваться геометрическими характеристиками поперечных сечений элементов, т.е.фактически их формой и размерами, так как их изменение приводит к изменению усилийв связях и новому распределению усилий во всех элементах системы.5. При расчете статически неопределимых систем необходимо заранее выбратьматериал конструкции, так как необходимо знать его модули упругости.6. В статически неопределимых системах температурное воздействие, осадка опор,неточности изготовления и монтажа вызывают появление дополнительных усилий.Метод сил. При расчете по м е т о д у с и л основными искомыми величинамиявляются усилия в лишних связях. Знание усилий в лишних связях позволит по методусечений выполнять полный расчет по определению усилий, возникающих в поперечныхсечениях элементов заданной системы.Степень статической неопределимости системыПеред расчетом статически неопределимой конструкции необходимо сначалаопределить степень статической неопределимости рассматриваемой системы. Длябалок и простых рам степень статической неопределимости равна числу лишних опорныхсвязей. В каждой связи возникает опорная реакция, поэтому степень статическойнеопределимости можно найти, сосчитав разность между количеством неизвестныхопорных реакций и числом независимых уравнений статики.Рис.1Например, балка на рис. 1, а является один раз статически неопределимой, таккак имеет 4 связи и 4 неизвестные опорные реакции, а количество независимыхуравнений равновесия – 3. В раме, показанной на рис.

Источник

8.6. Теория прочности Мора

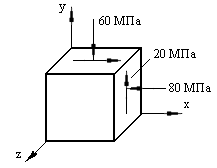
В отличие от изложенных выше теорий, теория Мора основывается не на гипотезах, а на экспериментальных данных. Зависимость между прочностными свойствами материала и видом напряженного состояния выводится и обосновывается с использованием кругов напряжений Мора. Для этого выбирается некоторое напряженное состояние, и одновременно увеличиваются его составляющие. 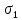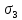Когда напряженное состояние станет предельным, на напряжениях и строится соответствующий им круг Мора. Среднее напряжение не учитывается. Опыт показывает, что ошибка при этом не превышает 10–15 %. Строится ряд таких кругов, соответствующих различным напряженным состояниям (рис. 8.2). Огибающая этих кругов, форма которой зависит от свойств материала, является его механической характеристикой.

Если огибающая предельных кругов Мора построена, то для ответа на вопрос, является ли напряженное состояние, характеризующееся главными напряжениями, предельным, и для оценки прочности материала следует построить для и круг напряжений в опасной точке материала. Прочность будет обеспечена, если он целиком лежит внутри огибающей. Для нахождения коэффициента запаса следует определить, во сколько раз необходимо увеличить и , чтобы круг касался огибающей.

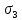
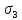
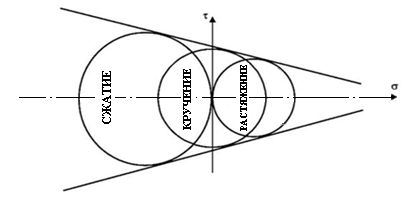
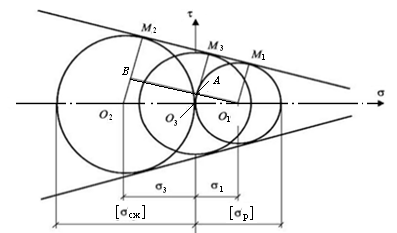
Для построения действительной огибающей предельных кругов Мора потребовалось бы опытным путем исследовать всевозможные напряженные состояния. Это неосуществимая задача, поэтому на практике действительную огибающую заменяют прямыми касательными лишь к двум предельным кругам, соответствующим опытам на одноосное растяжение и сжатие.

Рис. 8.2. Огибающая кругов Мора для различных напряженных

Условие прочности для промежуточного напряженного состояния с главными напряжениями и предельным кругом Мора с центром в точке О₃ (рис. 8.3) получим из следующих геометрических соотношений.

Проведем прямые О₁М₁, О₂М₂ и О₃ М₃,соединяющие центры предельных кругов Мора и точки их касания с предельной прямой, а также отрезок BО₁ параллельный М₁М₂. Из подобия ∆О₁О₂В и ∆О₁О₃А получим следующие зависимости:

Рис. 8.3. Схема для получения условия прочности Мора

Учитывая эти обозначения, преобразуем последнее равенство к виду:

Тогда получим условие прочности по теории Мора:

Если материал одинаково сопротивляется растяжению и сжатию, т. е. , теория прочности Мора совпадает с третьей теорией.

Выводы. Таким образом, разрушение материала может происходить путем отрыва одной части от другой и путем среза. Как правило, разрушение путем отрыва происходит хрупко, без заметных остаточных деформаций. Разрушение путем среза сопровождается пластическими деформациями. Поэтому первую и вторую теории можно применять для оценки прочности хрупких материалов, а третью и четвертую – пластических. Теория Мора позволяет учитывать разное сопротивление материала растяжению и сжатию.

8.7. Пример расчета

Задача 1. В опасной точке нагруженной детали напряженное состояние оказалось таким, как указано на схеме (рис. 8.4). Проверить прочность детали по третьей теории прочности, если [σ] = 160 МПа.

Рис. 8.4. Схема опасной точки

Задача 2. В опасной точке нагруженной детали напряженное состояние оказалось таким, как указано на схеме (рис. 8.5). Проверить прочность материала по третьей и четвертой теориям прочности, если σ_р = σ_сж и [σ] = 160 МПа.

Рис. 8.5. Схема опасной точки

.

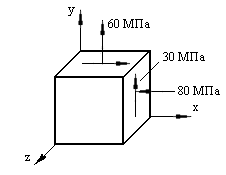
Задача 3. В опасной точке нагруженной детали напряженное состояние оказалось таким, как указано на схеме (рис. 8.6). Проверить прочность материала по четвертой теории прочности, если [σ] = 90 МПа.

Рис. 8.6. Схема опасной точки

Источник