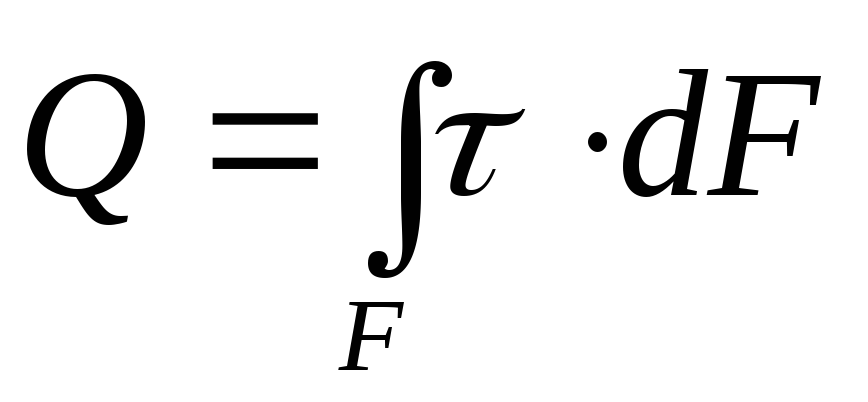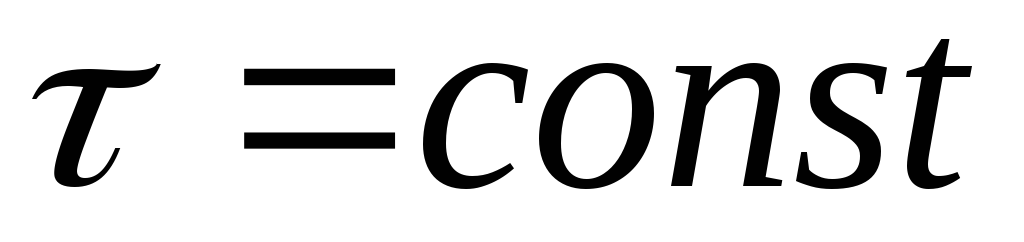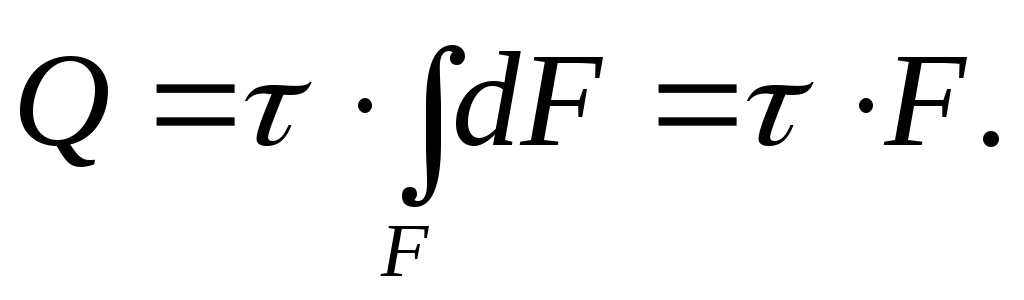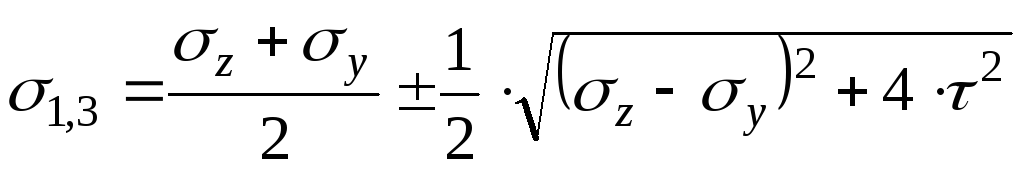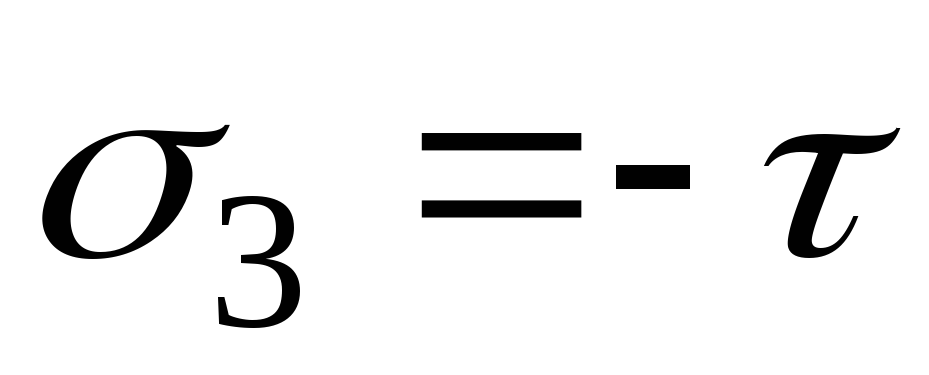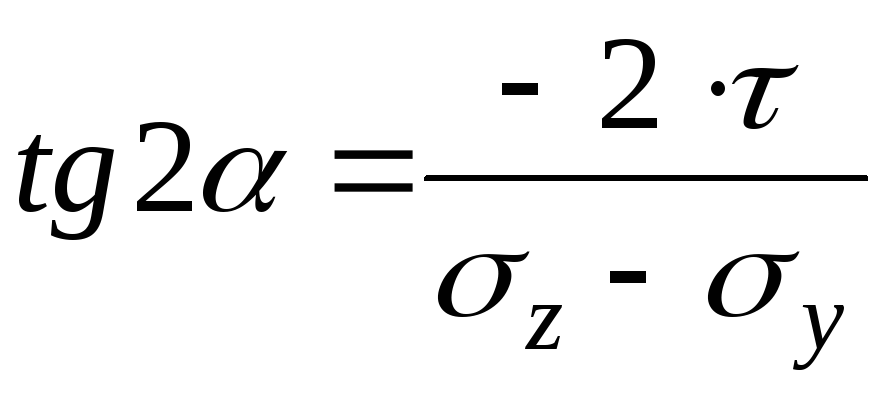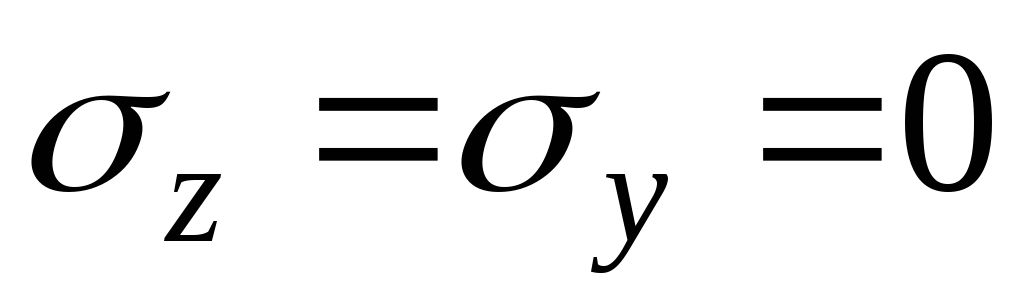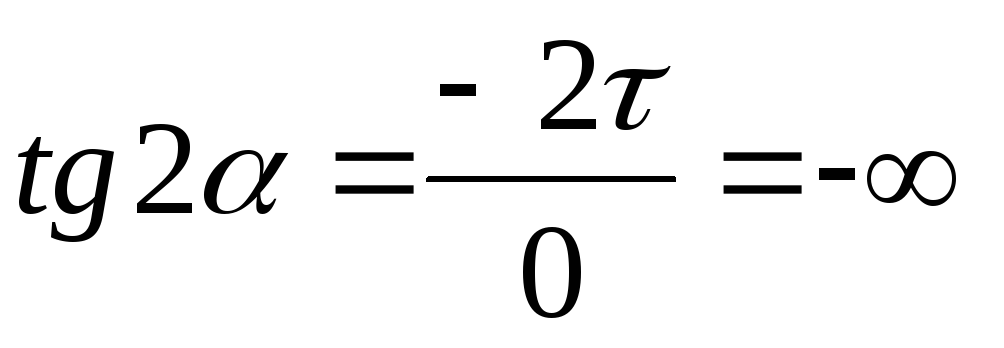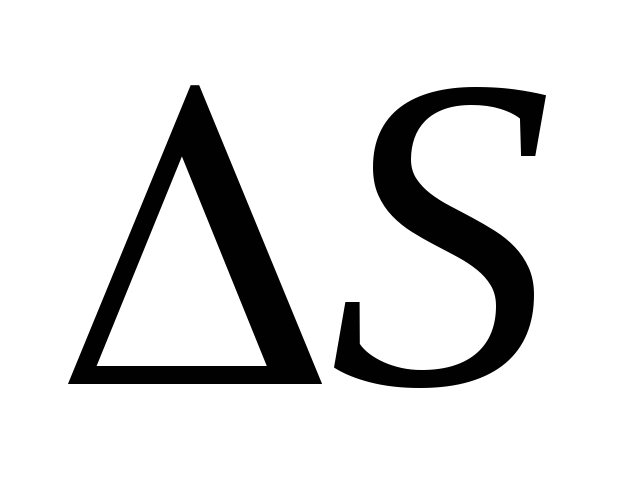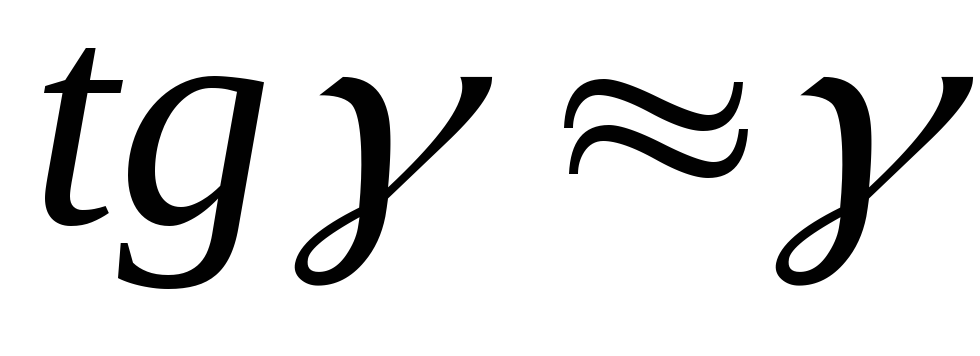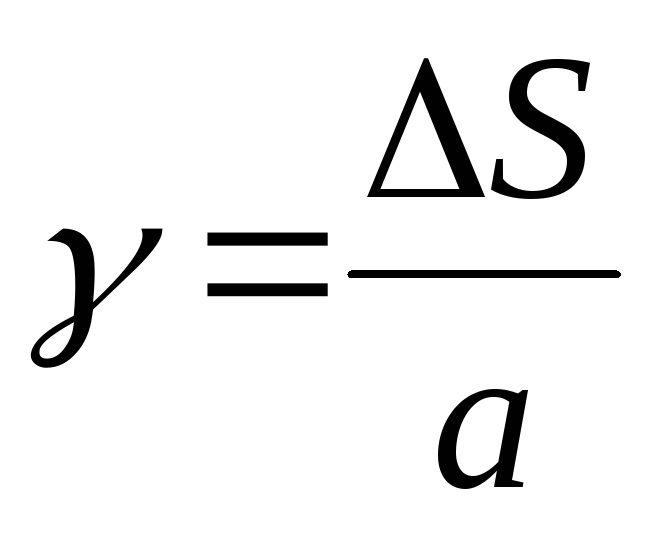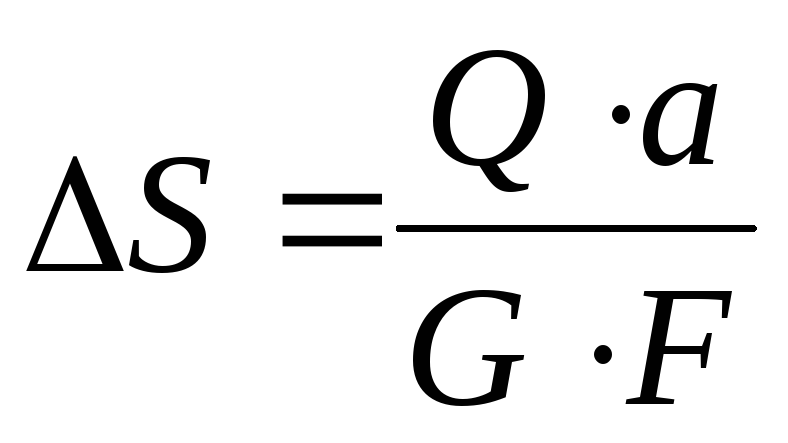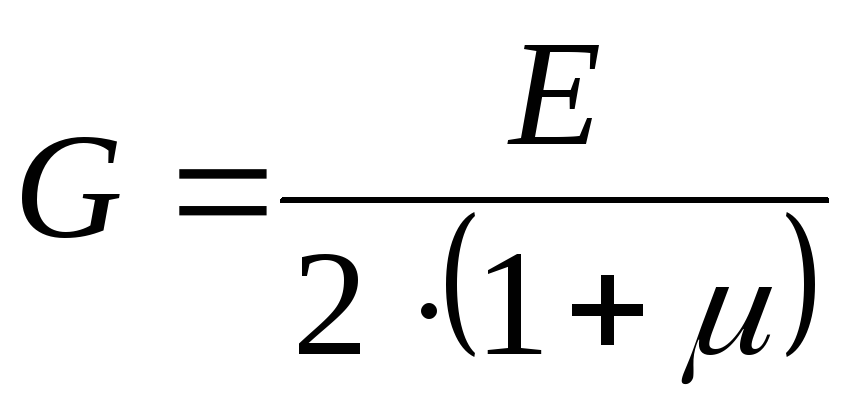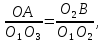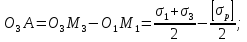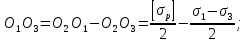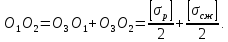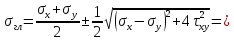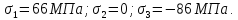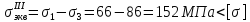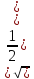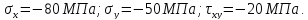Теория прочности мора вывод

Теория прочности мора (пятая гипотеза прочности)

теории кротовой прочности, в отличие от вышеприведенной теории, установлено, что прочностные характеристики материала в некоторой степени зависят от типа напряженного состояния. Получить такую зависимость и оправдать Рис 325Л Для космоса постройте три круга напряжения Используйте предложенный

мы рассматриваем приближение, которое, основываясь на существующих экспериментах, не учитывает влияние напряжения а*, а прочностные характеристики материала связаны только с напряжением- * Эксперимент показывает, что погрешность от игнорирования напряжения А2 не превышает 10-15%. Таким образом, только один из трех кругов, то есть самый большой, считается 379A3. Этот круг Мор называл главным кругом. С в случае напряжения тока?! И О3 встречает государство окончательного давления материала,

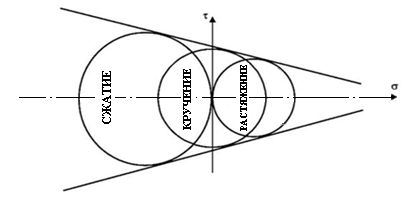
соответствуя основной круг также вызван пределом. В качестве примера приведем рисунок. 326 представляет три предельных круга для материалов, которые были испытаны на растяжение, сжатие и кручение. В то же время было установлено, что предельное напряжение при сжатии, которое указывает на АОС, больше, чем АОР при растяжении, то есть АОС кор. Когда вы рисуете огибающую этих кругов, это обычно кривая, которая пересекает ось a в определенно

• точке C. Эта точка соответствует полному растяжению с предельным напряжением, определяемым абсциссой точки с (см. Рисунок). 326). Кротовая окружность в этом случае превращается в точку, так как напряжения A1, A2 и a3 равны друг другу. Итак, если у вас есть некоторый предельный круг и его оболочка, вы можете предположить, что напряженное состояние, которое является

основным кругом, связанным с оболочкой, также является пределом. Для риса. 326 указывает на то, что семья имеет предел различных комбинаций субъектов с точки зрения подверженности стрессу. Как видно из рисунка, огибающая окружности определяет зависимость этих напряжений от типа напряженного состояния. Таким образом, на практике фактическая огибающая заменяется только касательными в двух окружностях, построенных по опыту растяжения и сжатия, поскольку получение фактической

огибающей предельного круга, построенного для всех возможных напряженных состояний, требует экспериментального исследования этих Людмила Фирмаль

напряженных состояний. 327). Эти линии служат границей региона Государственный 380prochnostnyh. При этом устанавливается линейная зависимость между напряжением и О3, основной круг которой касается этих линий:°1+6а3. (12.34) такое уравнение основано на простой геометрической зависимости, вытекающей из сходства треугольников в связи, вытекающей из сходства DL3CC2 и^A1C1C2 327). Учитывая Ники, вы можете испечь:^? И, Треугольник- Куда? (12.36 утра)) (12.35 утра)) Замена значения(12.36) (12.35) приводит к простому преобразованию в уравнение (12.34). Поскольку последнее должно быть верно в случае растяжения и сжатия, не прибегая к указанному преобразованию, коэффициенты a и Z3 для любой

соответствующим формулам второй теории прочности. Только роль их коэффициента Пуассона может учитывать различное сопротивление растяжению и сжатию материала, что является преимуществом теории крота по сравнению с другими теориями. Для материалов, одинаково устойчивых как к растяжению, так и к сжатию, т. е.

предельной окружности параллельна оси а(рис. 328). Теория Мора применима главным образом к хрупким материалам. Следует отметить, что наиболее достоверным результатом приведения в напряженное состояние является то, что окружность занимает положение в промежутке между окружностями растяжения и сжатия.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

3.7.5 Теория Мора

=(3.16)

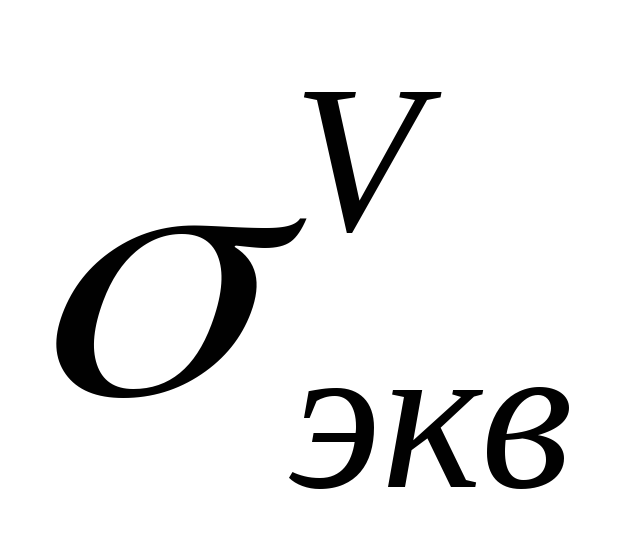
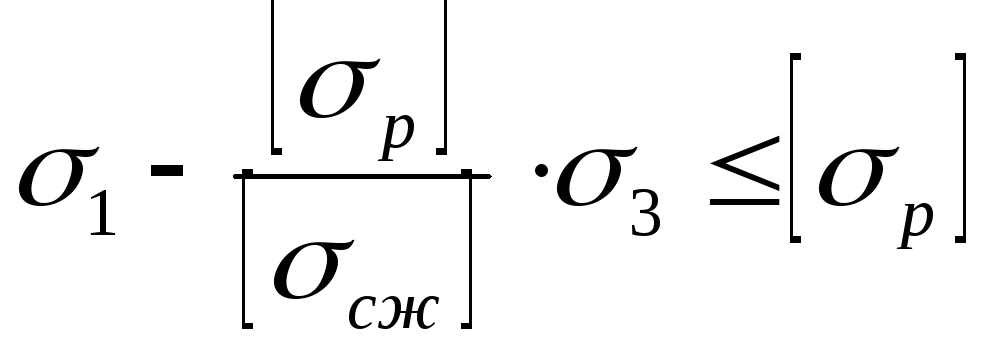
где 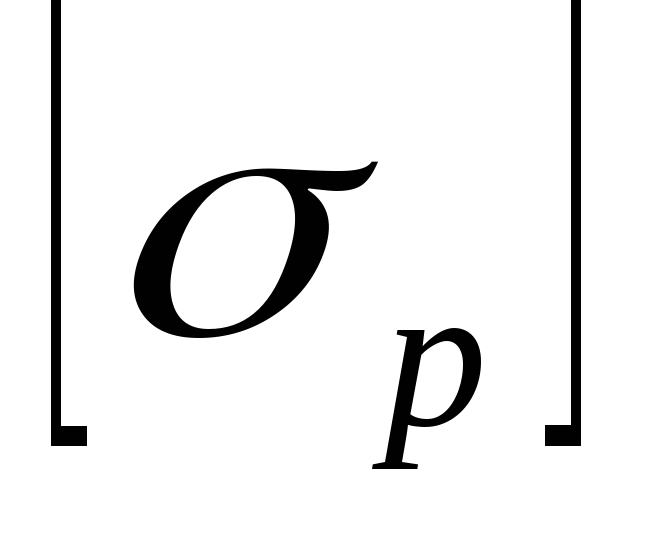— допускаемое напряжение на растяжение;— на сжатие.

Теория прочности Мора позволяет установить сопротивление разрушению материалов, обладающих разными сопротивлениями растяжению и сжатию (хрупкие материалы). Опыты показывают, что достаточно точные результаты гипотеза Мора дает для напряженных состояний смешанного типа, то есть для тех случаев, когда главные нормальные напряжения имеют разные знаки.

Таким образом, для практических расчетов следует рекомендовать третью и четвертую теории прочности для материалов одинаково работающих на растяжение и сжатие, и теорию Мора – для материалов, различно сопротивляющихся растяжению и сжатию, то есть для хрупких материалов.

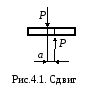
4 Сдвиг

4.1 Определение внутренних усилий и напряжений при сдвиге

Сдвиг – вид сопротивления, при котором стержень нагружен двумя равными силами (на малом расстоянии друг от друга), перпендикулярными к оси бруса и направленными в противоположные стороны.

Примером такого действия сил на брус может быть разрезание ножницами прутьев, деформация заклепок, болтов, сварных швов между металлическими листами и т. п.

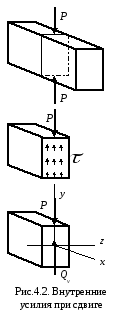
Мысленно рассекая брус поперечным сечением перпендикулярным продольной оси определим внутренние усилия, действующие в сечении бруса при сдвиге.

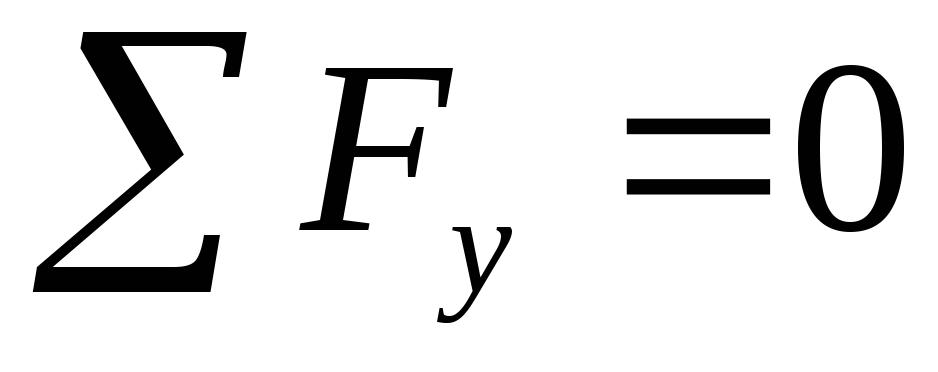
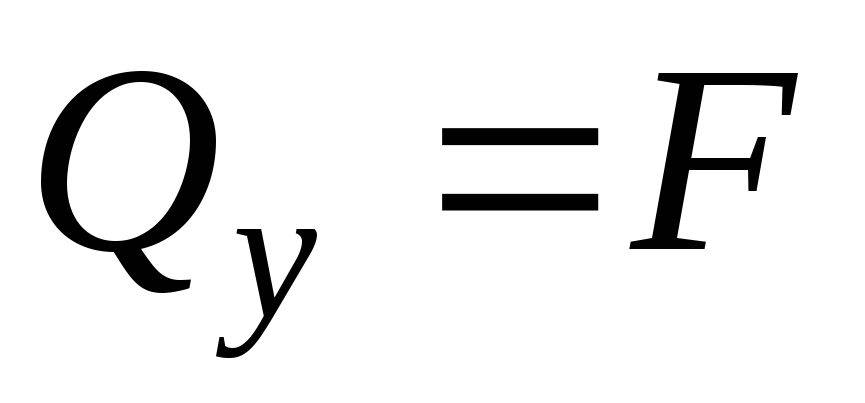
В данном случае нагружения из шести уравнений равновесия лишь одно не нулевое: , следовательно.

При сдвиге в сечении элемента возникает только одно внутреннее усилие – поперечная сила (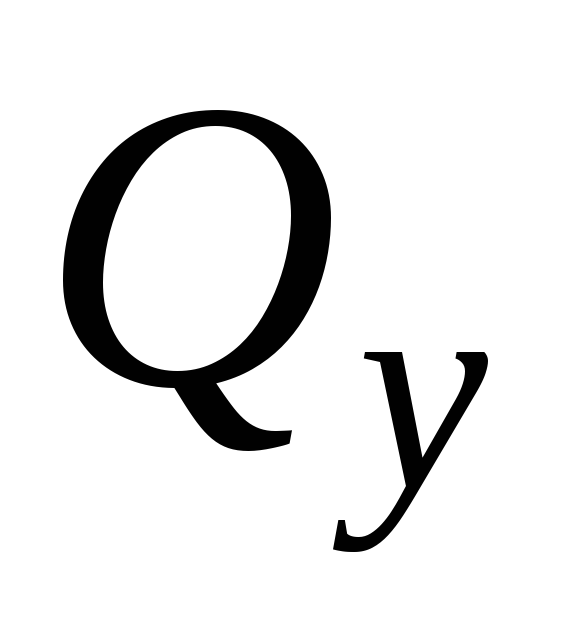или).

Так как единственное внутреннее усилие, возникающие при сдвиге (поперечная сила 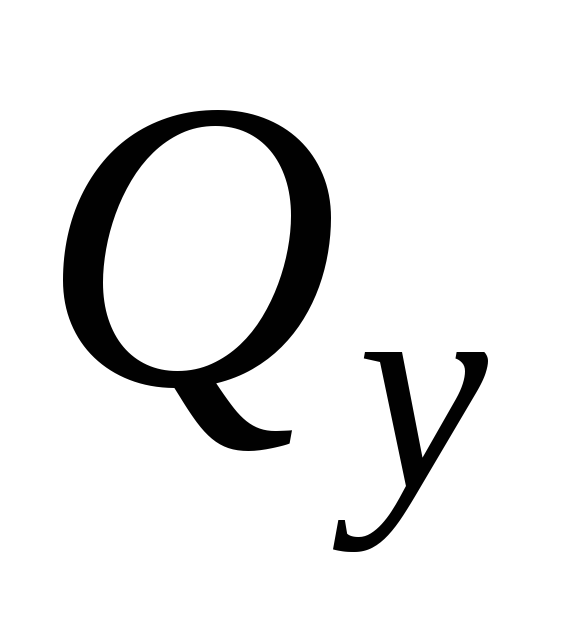или ), лежит в плоскости поперечного сечения, то и напряжения, лежат в плоскости сечения стержня. То есть при сдвиге в точках поперечного сечения стержня возникают только касательные напряжения .

Таким образом, поперечная сила, возникающая в сечении

. (4.1)

При сдвиге считают, что касательные напряжения равномерно распределены по площади поперечного сечения, т.е. , поэтому

(4.2)

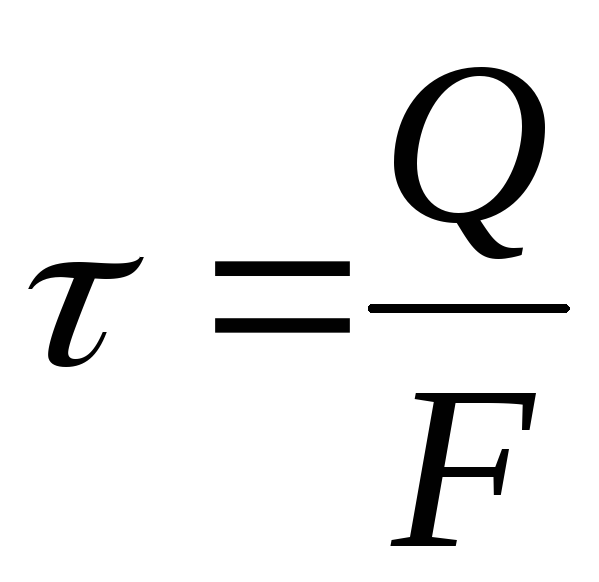
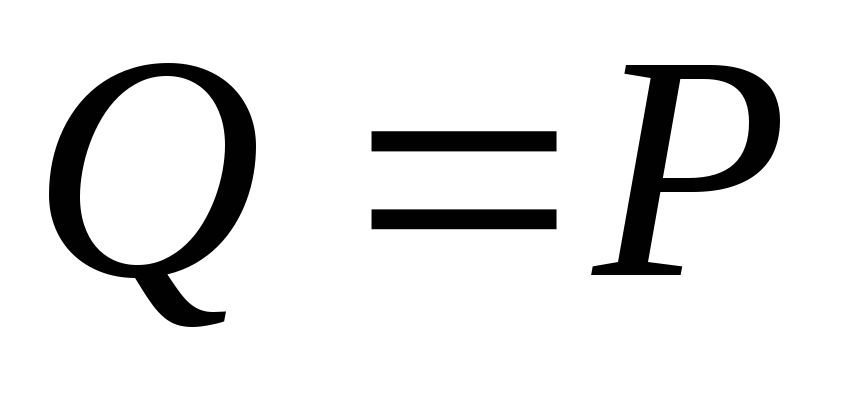
Касательные напряжения при сдвиге определяются по формуле , а так как, то

. (4.3)

4.2 Напряженное состояние при сдвиге

Чистый сдвиг – частный случай плоского напряженного состояния, при котором по граням прямоугольного элемента действуют только касательные напряжения.

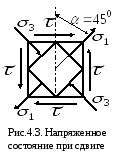
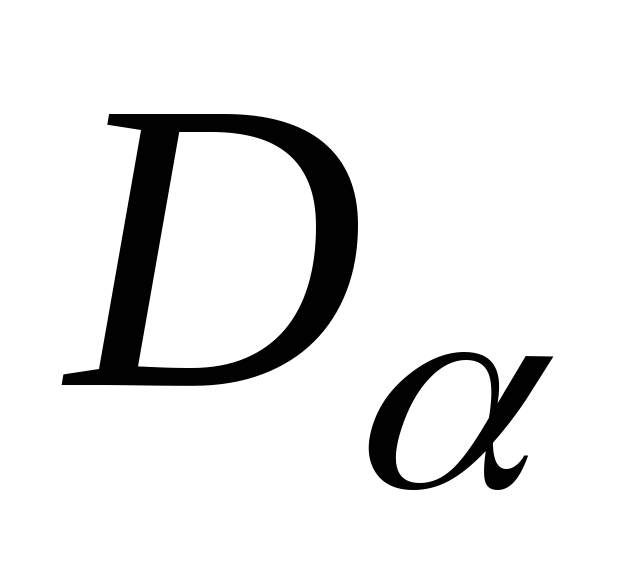
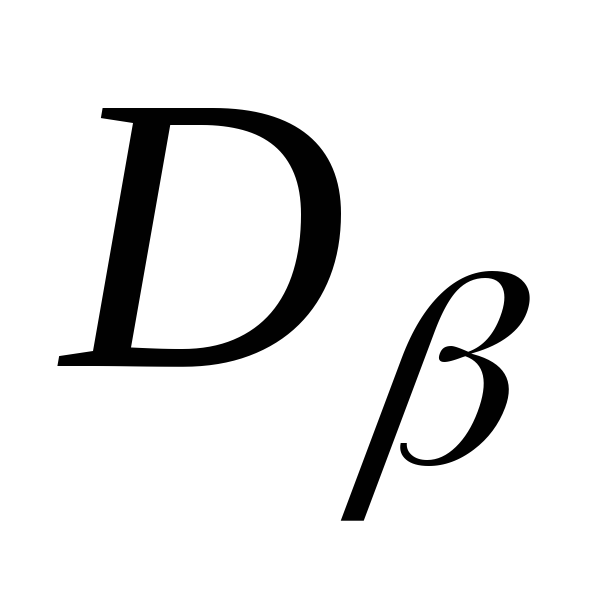
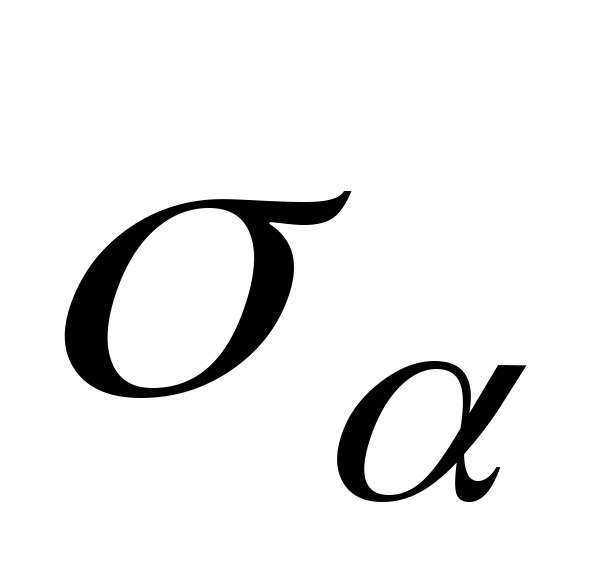
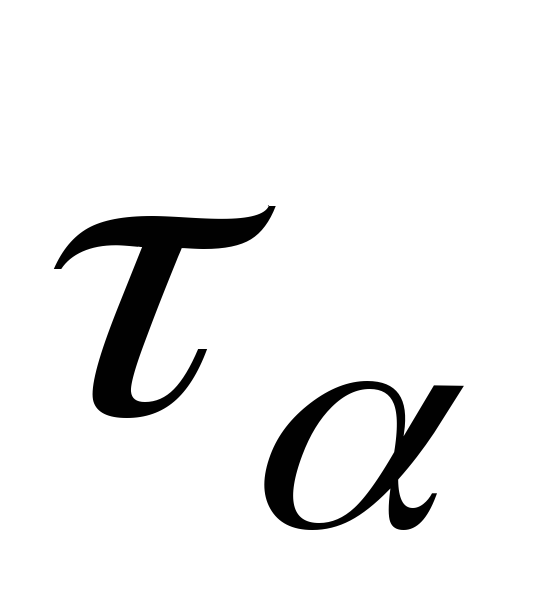
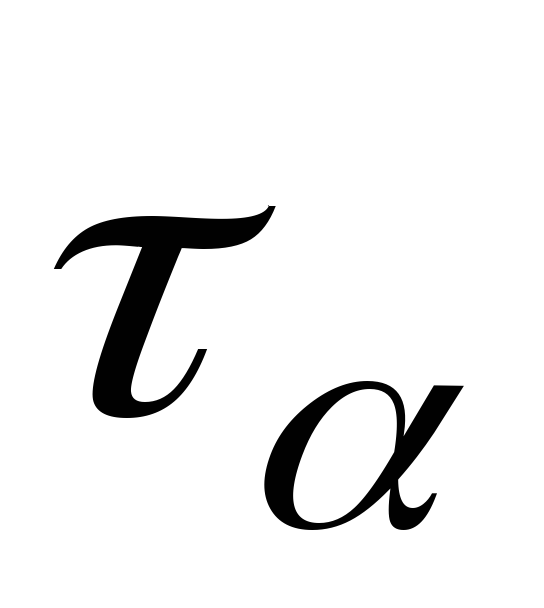
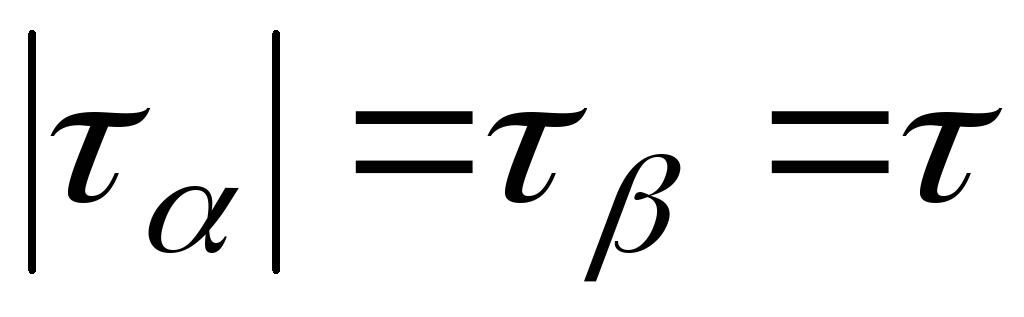
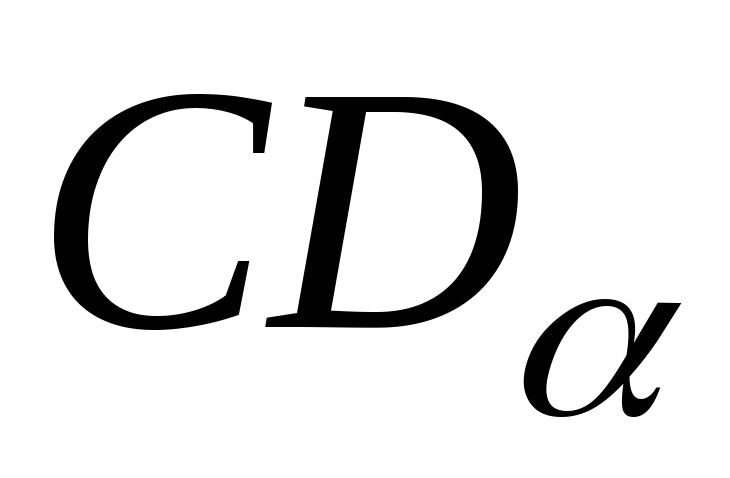
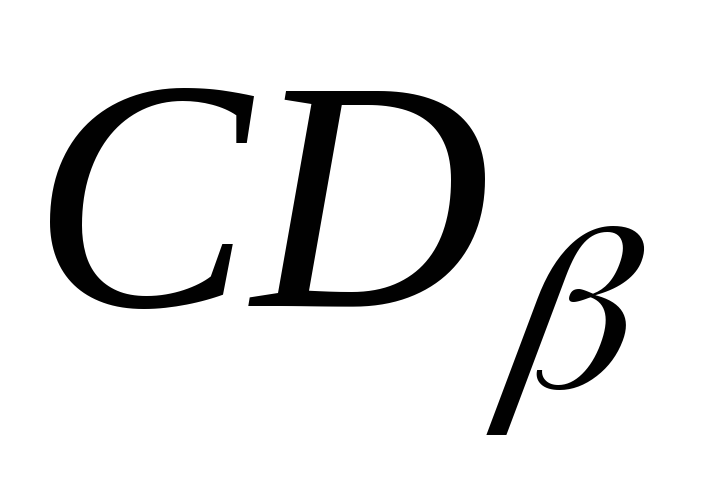
Построим круг Мора: Точкииточки, соответствующие напряженному состоянию на указанных взаимно перпендикулярных площадкахис координатами (;) т.е. (0; —) и (;) т.е. (0;) соответственно (). Через эти две точки проводится окружность радиусомили(точка С – центр круга Мора). В точках где круг Мора пересекает осьможно найти величину главных нормальных напряжений(так как касательные напряжения равны нулю.

Определим величину и направление главных напряжений при чистом сдвиге:

,(4.4)

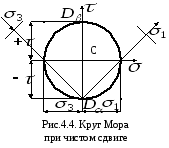
так как , можно записатьи

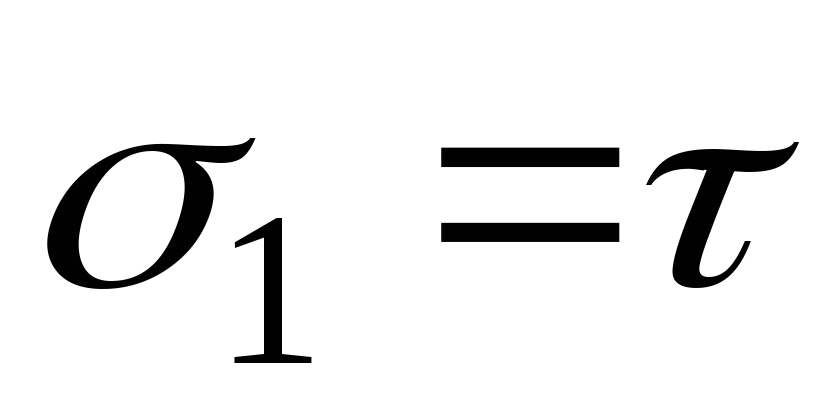
Направление главных площадок определяется углом , который найдем по формуле:

; (4.5)

учитывая что ,

;

; .

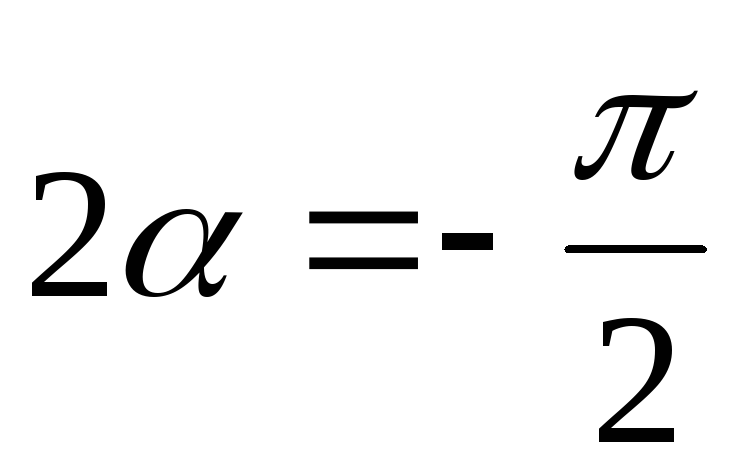
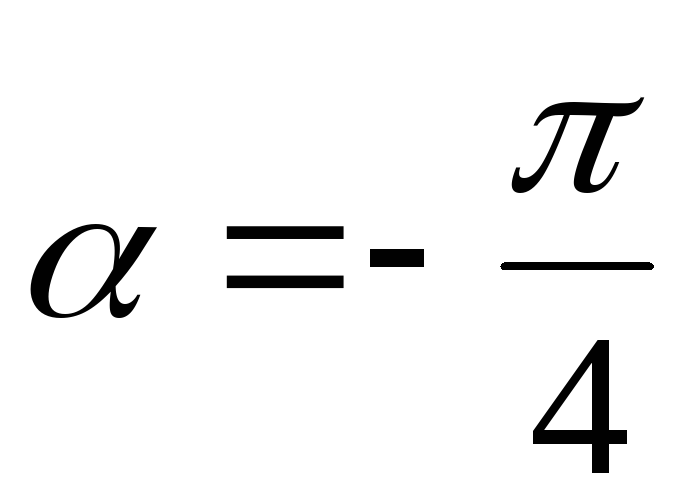
4.3 Деформации при сдвиге

Рассмотрим деформацию квадратного элемента при сдвиге.

Рис.4.5. Деформация квадратного элемента при сдвиге.

оскольку по граням элемента не действуют нормальные напряжения, то 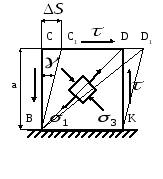вдоль граней нет и удлинений. В то же время диагональBD, совпадающая с направлением , удлинится, а диагональ СК, совпадающая с направлением сжимающего напряжения, укоротиться. В результате квадратBCDK трансформируется в ромб BC₁D₁K, без изменения длины граней. Таким образом, деформация сдвига характеризуется изменением первоначально прямых углов.

Малый угол , на который изменяется первоначально прямой угол элемента при сдвиге, называетсяуглом сдвига или относительным сдвигом.

Величину абсолютного смещения грани обозначают и называютабсолютным сдвигом.

Из прямоугольного треугольника ВСС₁:

(4.6)

Учитывая малость угла можно считать, что , тогда окончательно запишем взаимосвязь между относительным и абсолютным сдвигом элемента

(4.7)

При сдвиге можно экспериментально построить диаграмму сдвига, аналогичную диаграмме растяжения, на которой также в начале нагружения будет прямолинейный участок деформации по закону Гука.

Закон Гука при сдвиге:

или , (4.8)

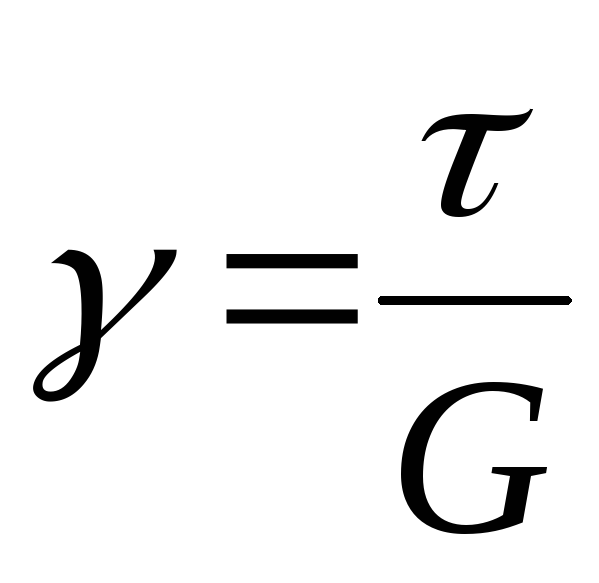
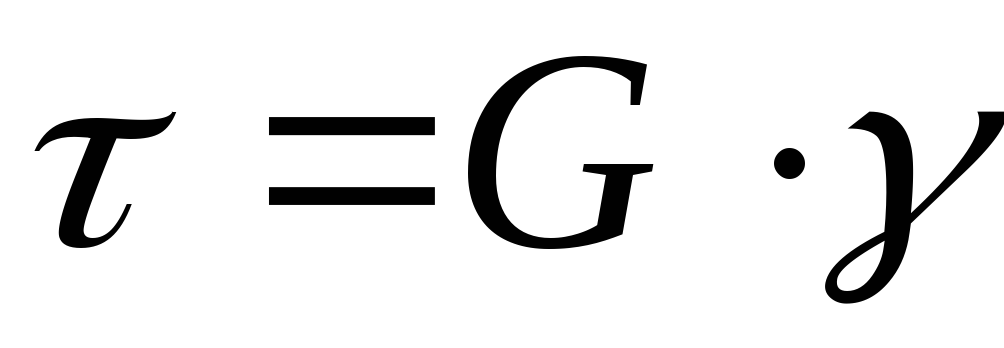
где G – модуль касательной упругости или модуль сдвига (модуль упругости второго рода), которая является константой для данного материала.

Закон Гука при сдвиге через абсолютные деформации:

, (4.9)

где а – расстояние между сдвигаемыми гранями; F – площадь грани.

Взаимосвязь между упругими постоянными:

. (4.10)

Источник

8.6. Теория прочности Мора

В отличие от изложенных выше теорий, теория Мора основывается не на гипотезах, а на экспериментальных данных. Зависимость между прочностными свойствами материала и видом напряженного состояния выводится и обосновывается с использованием кругов напряжений Мора. Для этого выбирается некоторое напряженное состояние, и одновременно увеличиваются его составляющие. 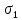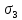Когда напряженное состояние станет предельным, на напряжениях и строится соответствующий им круг Мора. Среднее напряжение не учитывается. Опыт показывает, что ошибка при этом не превышает 10–15 %. Строится ряд таких кругов, соответствующих различным напряженным состояниям (рис. 8.2). Огибающая этих кругов, форма которой зависит от свойств материала, является его механической характеристикой.

Если огибающая предельных кругов Мора построена, то для ответа на вопрос, является ли напряженное состояние, характеризующееся главными напряжениями, предельным, и для оценки прочности материала следует построить для и круг напряжений в опасной точке материала. Прочность будет обеспечена, если он целиком лежит внутри огибающей. Для нахождения коэффициента запаса следует определить, во сколько раз необходимо увеличить и , чтобы круг касался огибающей.

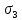
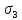
Для построения действительной огибающей предельных кругов Мора потребовалось бы опытным путем исследовать всевозможные напряженные состояния. Это неосуществимая задача, поэтому на практике действительную огибающую заменяют прямыми касательными лишь к двум предельным кругам, соответствующим опытам на одноосное растяжение и сжатие.

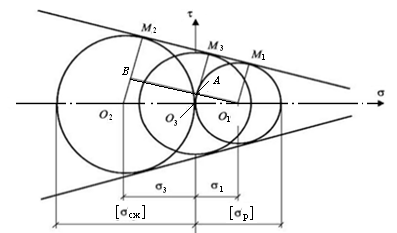
Рис. 8.2. Огибающая кругов Мора для различных напряженных

Условие прочности для промежуточного напряженного состояния с главными напряжениями и предельным кругом Мора с центром в точке О₃ (рис. 8.3) получим из следующих геометрических соотношений.

Проведем прямые О₁М₁, О₂М₂ и О₃ М₃,соединяющие центры предельных кругов Мора и точки их касания с предельной прямой, а также отрезок BО₁ параллельный М₁М₂. Из подобия ∆О₁О₂В и ∆О₁О₃А получим следующие зависимости:

Рис. 8.3. Схема для получения условия прочности Мора

Учитывая эти обозначения, преобразуем последнее равенство к виду:

Тогда получим условие прочности по теории Мора:

Если материал одинаково сопротивляется растяжению и сжатию, т. е. , теория прочности Мора совпадает с третьей теорией.

Выводы. Таким образом, разрушение материала может происходить путем отрыва одной части от другой и путем среза. Как правило, разрушение путем отрыва происходит хрупко, без заметных остаточных деформаций. Разрушение путем среза сопровождается пластическими деформациями. Поэтому первую и вторую теории можно применять для оценки прочности хрупких материалов, а третью и четвертую – пластических. Теория Мора позволяет учитывать разное сопротивление материала растяжению и сжатию.

8.7. Пример расчета

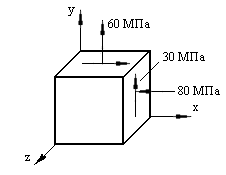
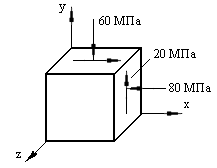
Задача 1. В опасной точке нагруженной детали напряженное состояние оказалось таким, как указано на схеме (рис. 8.4). Проверить прочность детали по третьей теории прочности, если [σ] = 160 МПа.

Рис. 8.4. Схема опасной точки

Задача 2. В опасной точке нагруженной детали напряженное состояние оказалось таким, как указано на схеме (рис. 8.5). Проверить прочность материала по третьей и четвертой теориям прочности, если σ_р = σ_сж и [σ] = 160 МПа.

Рис. 8.5. Схема опасной точки

.

Задача 3. В опасной точке нагруженной детали напряженное состояние оказалось таким, как указано на схеме (рис. 8.6). Проверить прочность материала по четвертой теории прочности, если [σ] = 90 МПа.

Рис. 8.6. Схема опасной точки

Источник