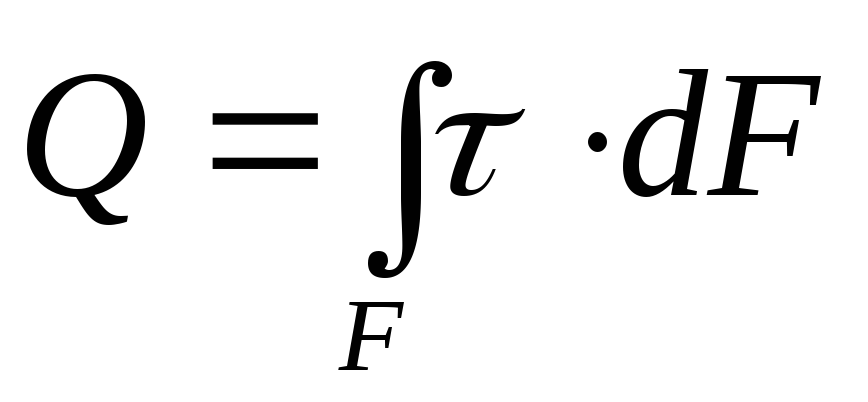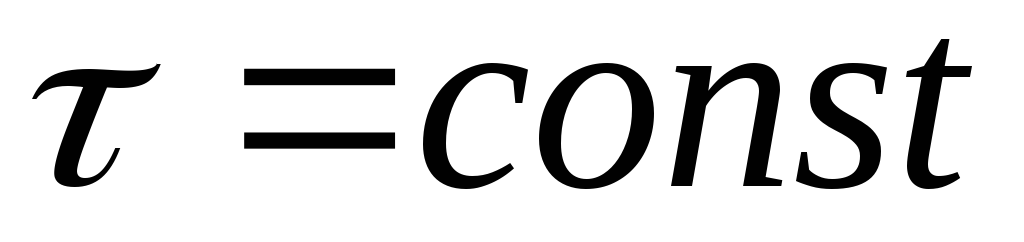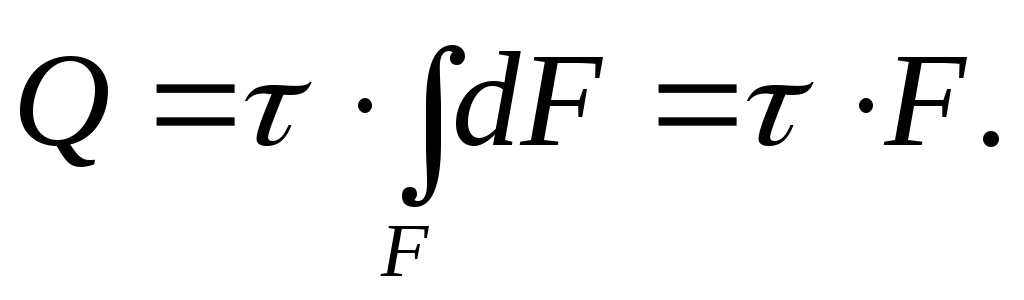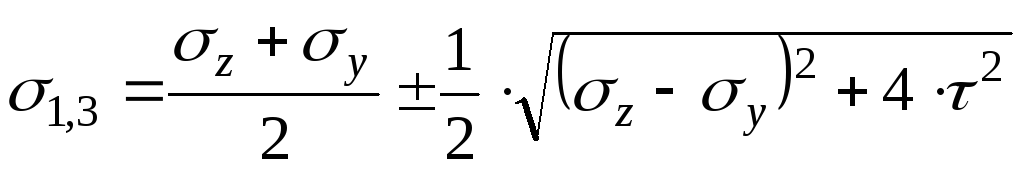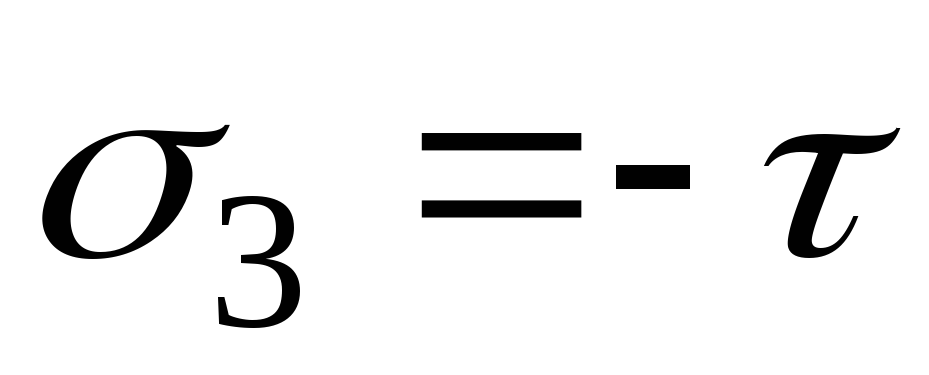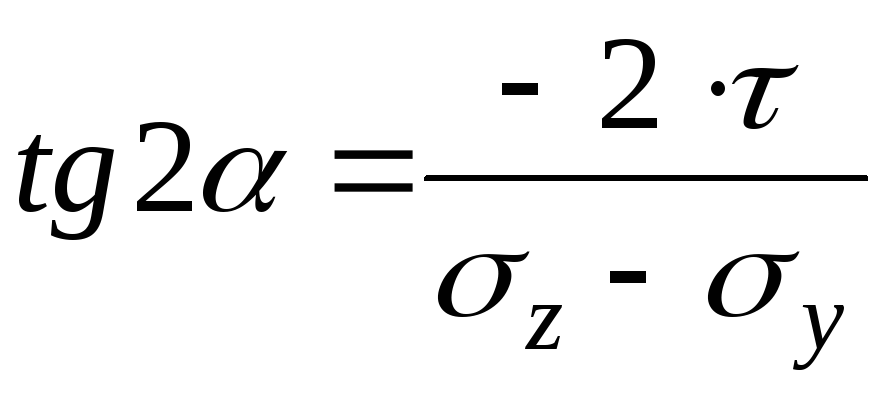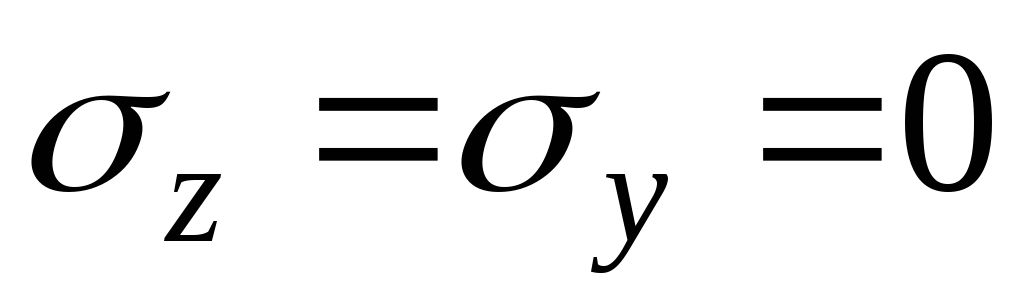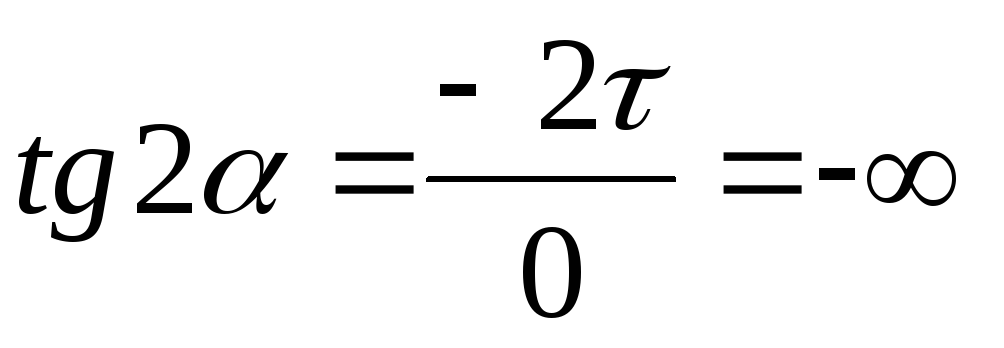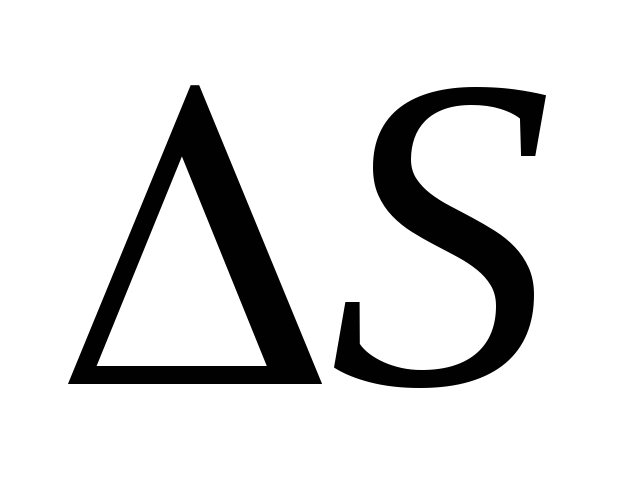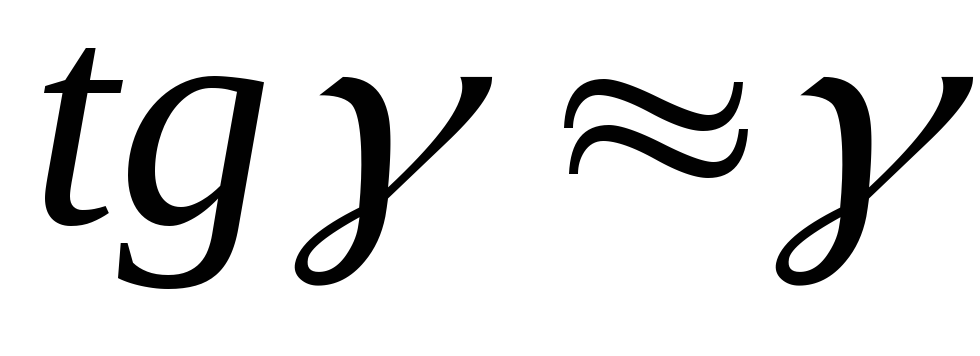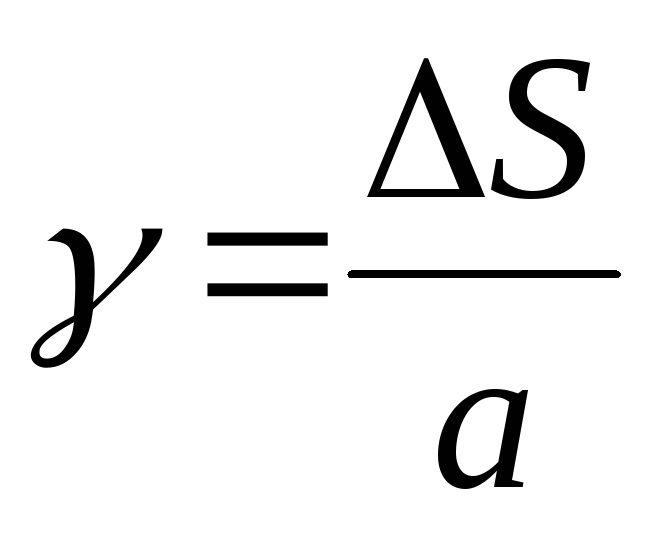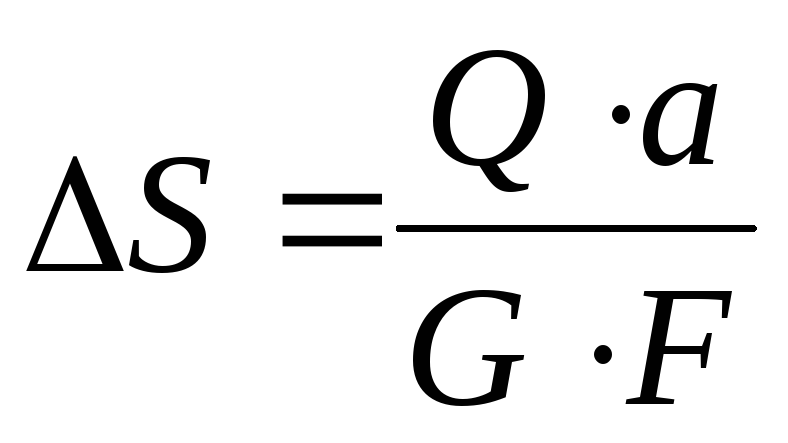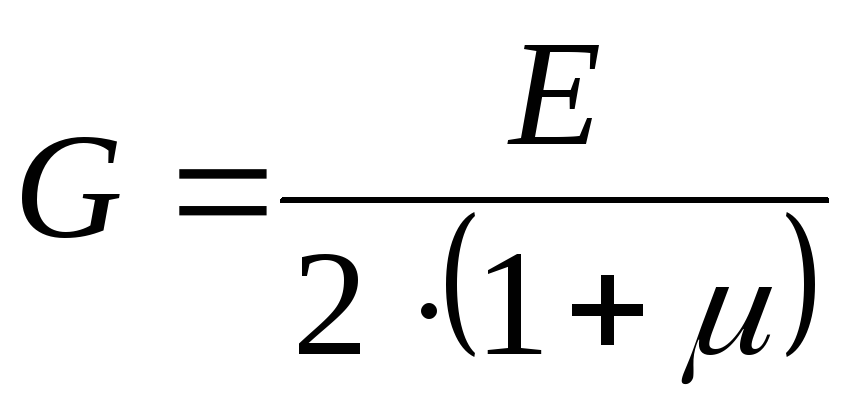Теория прочности мора формулы

Техническая механика

В предыдущей статье мы рассматривали случаи сочетания основных деформаций, когда в поперечных сечениях бруса возникают только нормальные напряжения, и суммарное напряжение в каждой точке можно было рассчитать простым алгебраическим сложением. Однако часто имеют место случаи сочетания основных деформаций, при которых в поперечных сечениях возникают и нормальные, и касательные напряжения, распределенные по площади сечений неравномерно и по разным законам.
Для таких случаев опытное определение величин, характеризующих прочность, невозможно, поэтому при оценке прочности детали приходится основываться на механических характеристиках данного материала, полученных из диаграммы растяжения.

Как известно, при растяжении прочность пластичных материалов характеризуется пределом текучести, а прочность хрупких материалов – пределом прочности. Эти напряжения считаются предельными, и в зависимости от их величины вычисляют допускаемые напряжения. Для упрощения расчетов величины напряжений при сочетании деформаций вводят понятие эквивалентного (равноопасного) напряжения.

Напряженные состояния при сочетании основных деформаций и одноосном растяжении называют равноопасными или эквивалентными, если их главные напряжения отличаются от предельного для данного материала в одинаковое число раз, т. е. коэффициенты запаса прочности для эквивалентных напряжений одинаковы.
Иными словами, эквивалентным считается такое напряжение при простом одноосном растяжении, которое равноопасно данному сочетанию основных деформаций.
Таким образом, условие прочности при сочетании основных деформаций, когда в поперечных сечениях действуют и нормальные и касательные напряжения, будет иметь вид: σ_экв ≤ [σ_p] .

Формулы для определения эквивалентных напряжений, которые затем сопоставляют с предельно допускаемыми, выводят на основании гипотез прочности.

Гипотезы прочности – это научные предположения об основной причине достижения материалом предельного напряженного состояния при сочетании основных деформаций.

В настоящее время при вычислении эквивалентных напряжений используют три гипотезы прочности: гипотезу наибольших касательных напряжений (или третья гипотеза прочности), гипотезу Мора (четвертая гипотеза прочности) и энергетическую гипотезу (пятая гипотеза прочности).
Применявшиеся ранее при расчетах первая (гипотеза Галилея) и вторая (гипотеза Мариотта-Сен-Венана) гипотезы прочности, основанные соответственно на наибольших нормальных напряжениях и линейных деформациях, в настоящее время не используются, поскольку плохо подтверждаются опытами.

Рассмотрим подробнее суть каждой из перечисленных гипотез прочности.

Третья теория прочности

Гипотеза наибольших касательных напряжений

Согласно этой гипотезе, предложенной в конце XVIII в., опасное состояние материала наступает тогда, когда наибольшие касательные напряжения достигают предельной величины.

Если рассмотреть элементарную площадку в наклонном сечении продольно растягиваемого бруса, то при помощи простых геометрических выкладок можно убедиться, что касательное напряжение в такой площадке достигает максимальной величины, когда сечение располагается под углом 45˚ к оси бруса. При этом величина касательного напряжения будет равна половине разности между максимальным и минимальным нормальным напряжением:

В частном случае, если σ_min = 0 , то τ_max = σ_max/2 .

Чтобы вывести формулу для вычисления эквивалентных напряжений по третьей теории прочности, рассмотрим брус, у которого в поперечном сечении действуют нормальные σ и касательные τ напряжения (см. рисунок) .

Внутри бруса вблизи от произвольной точки В вырежем бесконечно малую призму abc , у которой грань ab совпадает с поперечным, грань ac – с продольным сечениями, а грань bc является главной площадкой, на которой действует главное напряжение σ₀ .
Согласно закону парности касательных напряжений в грани ac призмы также будут действовать касательные напряжения τ .
Поскольку в продольном сечении бруса нормальных напряжений нет, то здесь мы имеем дело со случаем плоского напряженного состояния, который называют упрощенным.

Рассмотрим равновесие призмы abc , для чего спроецируем все действующие на нее силы на оси z и y . Площадь грани bc обозначим dA (элементарная площадка). Тогда:

Σ Z = 0; σ₀ dAsinφ — τ dA cosφ — σ dA sinφ = 0
Σ Y = 0; σ₀ dA cosφ — τ dA sinφ = 0 .

Разделив обе части равенства на dA , получим:

(σ₀ – σ) sinφ = τ cosφ; σ₀ cosφ = τ sinφ .

Оба равенства разделим на cosφ и, исключив из них tgφ , получим выражение:

τ / (σ₀ — σ) = σ₀ / τ , что равнозначно квадратному уравнению σ₀ 2 — σ₀σ – τ 2 = 0 .

Решая это уравнение, получим:

(Здесь и далее знак √ обозначает квадратный корень).

Таким образом, главные напряжения в наклонных площадках в зонах точки А бруса определяют по формулам:

σ_max = σ/2 + 1/2 √(σ 2 + 4τ 2 ) σ_min = σ/2 — 1/2 √(σ 2 + 4τ 2 ) .

Следовательно, исходя из формулы (1) , максимальные касательные напряжения можно найти по формуле:

Поскольку τ_пред = σ_пред/2 , а эквивалентное напряжение не должно превышать предельного, то, применяя гипотезу наибольших касательных напряжений, имеем:

В результате мы получили формулу для вычисления эквивалентных напряжений:

Гипотеза наибольших касательных напряжений хорошо подтверждается опытами, в особенности для пластичных материалов.

Четвертая теория прочности

Гипотеза Мора

Большой вклад в разработке методов определения напряжений при сложном напряженном состоянии внес немецкий ученый Кристиан Отто Мор (Christian Otto Mohr, 1835-1918 г.г.) .
Заслуги К.О.Мора в науке сопротивление материалов трудно переоценить — он является создателем одной из теорий прочности (теория прочности Мора), графических методов определения напряжений при сложном напряжённом состоянии (круг Мора).
Мор впервые применил расчёт конструкций на невыгодное загружение с помощью так называемых линий влияния, создал теорию расчёта статически неопределимых систем методом сил. Этот ученый разработал также метод расчёта неразрезных балок с помощью уравнений трех моментов, предложил графический метод построения упругой линии в простых и неразрезных балках.

Гипотеза Мора, предложенная им в начале XX века может быть сформулирована так:
Опасное состояние материала наступает тогда, когда на некоторой площадке осуществляется наиболее неблагоприятная комбинация нормального и касательного напряжений.

По сути, это усовершенствованная и обобщенная гипотеза наибольших касательных напряжений, рассмотренная ранее, тем не менее, она дает возможность определять эквивалентные напряжения в балках с меньшей степенью погрешности и применима при расчетах на прочность как пластичных, так и хрупких материалов.

Формула для вычисления эквивалентных напряжений, согласно гипотезе Мора имеет вид:

σ_экв = σ(1 – k)/2 + 1/2 (1 + k) √(σ 2 + 4τ 2 ) ,

Очевидно, что при k = 1 формула Мора тождественна формуле третьей теории прочности (гипотезе наибольших касательных напряжений).

Пятая, или энергетическая теория прочности

Энергетическая гипотеза

При деформации элементарной частицы тела в общем случае изменяются ее форма и объем. Таким образом, полная потенциальная энергия деформации состоит из двух частей: энергии формоизменения и энергии изменения объема.
Энергетическая гипотеза прочности, предложенная в начале XX века в качестве критерия перехода материала в предельное состояние принимает только энергию формоизменения.

Согласно этой гипотезе, опасное состояние материала в данной точке наступает тогда, когда удельная потенциальная энергия формоизменения для этой точки достигает предельной величины.

Формула для вычисления эквивалентных напряжений в соответствии с пятой (энергетической) теорией прочности имеет вид:

Эта формула хорошо подтверждается опытным путем для пластичных материалов и получила широкое распространение.

Следует отметить, что во всех приведенных выше формулах σ и τ — нормальные и касательные напряжения на площадке поперечного сечения, проходящего через опасную или предположительно опасную точку.

Источник

3.7.5 Теория Мора

=(3.16)

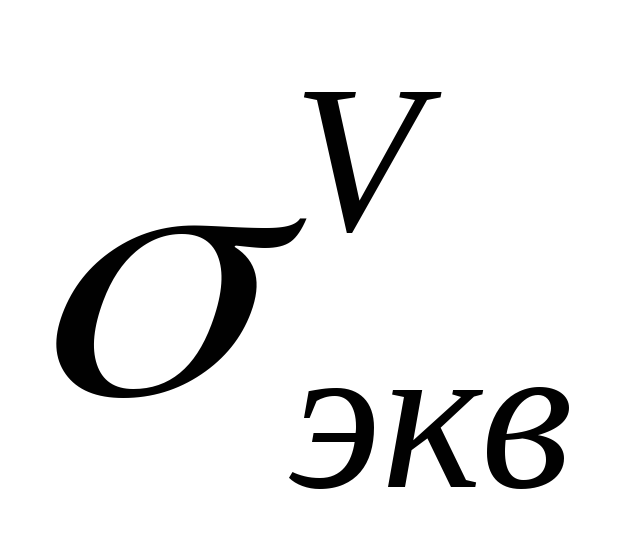
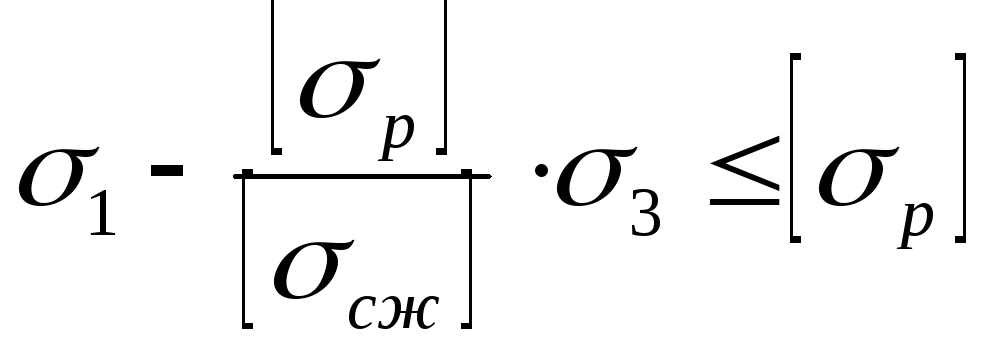
где 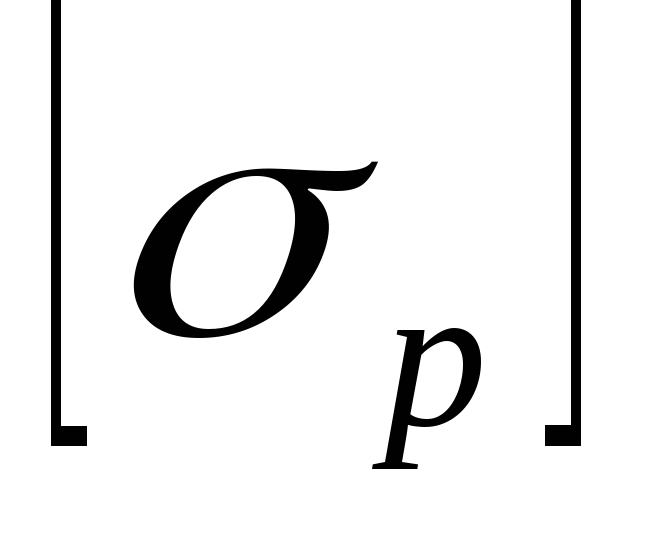— допускаемое напряжение на растяжение;— на сжатие.

Теория прочности Мора позволяет установить сопротивление разрушению материалов, обладающих разными сопротивлениями растяжению и сжатию (хрупкие материалы). Опыты показывают, что достаточно точные результаты гипотеза Мора дает для напряженных состояний смешанного типа, то есть для тех случаев, когда главные нормальные напряжения имеют разные знаки.

Таким образом, для практических расчетов следует рекомендовать третью и четвертую теории прочности для материалов одинаково работающих на растяжение и сжатие, и теорию Мора – для материалов, различно сопротивляющихся растяжению и сжатию, то есть для хрупких материалов.

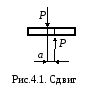
4 Сдвиг

4.1 Определение внутренних усилий и напряжений при сдвиге

Сдвиг – вид сопротивления, при котором стержень нагружен двумя равными силами (на малом расстоянии друг от друга), перпендикулярными к оси бруса и направленными в противоположные стороны.

Примером такого действия сил на брус может быть разрезание ножницами прутьев, деформация заклепок, болтов, сварных швов между металлическими листами и т. п.

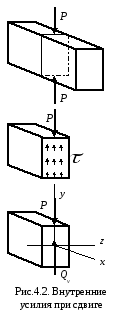
Мысленно рассекая брус поперечным сечением перпендикулярным продольной оси определим внутренние усилия, действующие в сечении бруса при сдвиге.

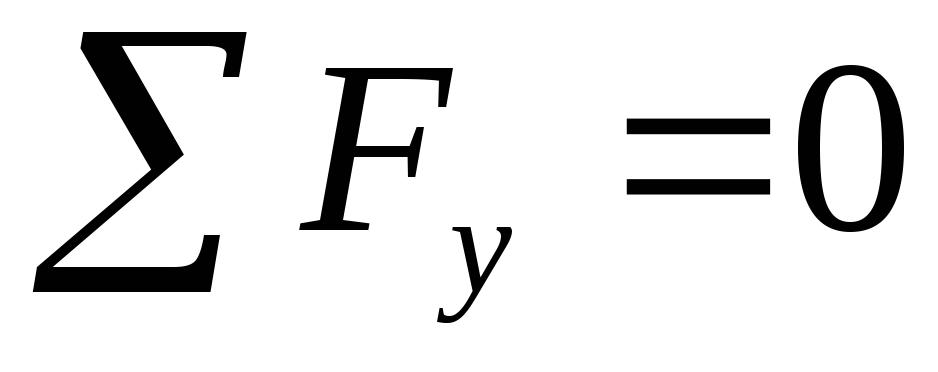
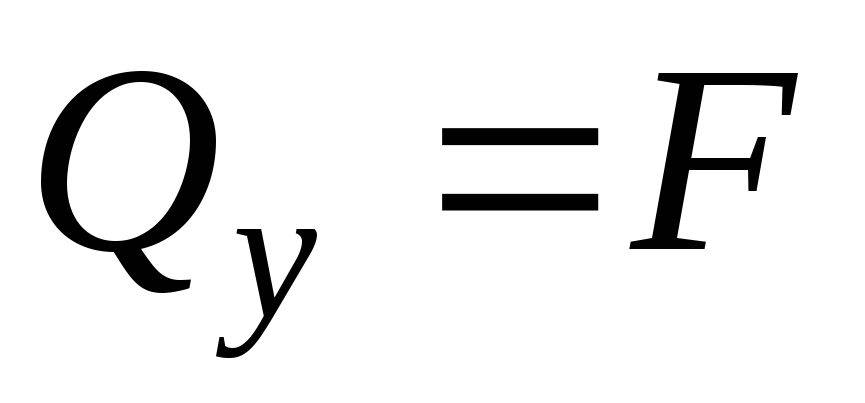
В данном случае нагружения из шести уравнений равновесия лишь одно не нулевое: , следовательно.

При сдвиге в сечении элемента возникает только одно внутреннее усилие – поперечная сила (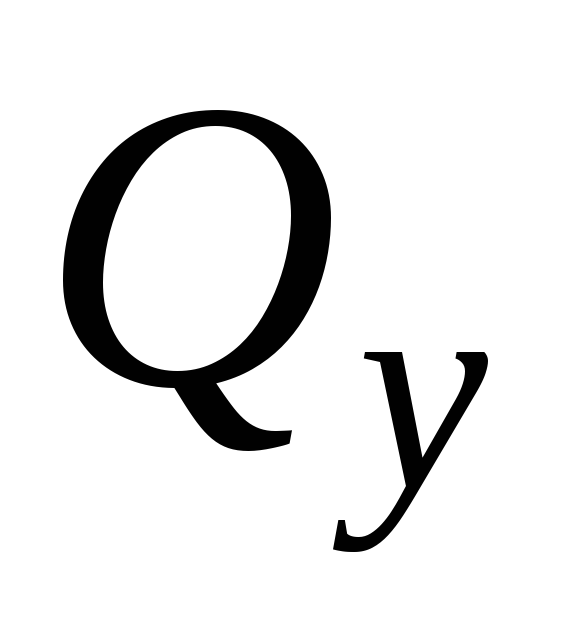или).

Так как единственное внутреннее усилие, возникающие при сдвиге (поперечная сила 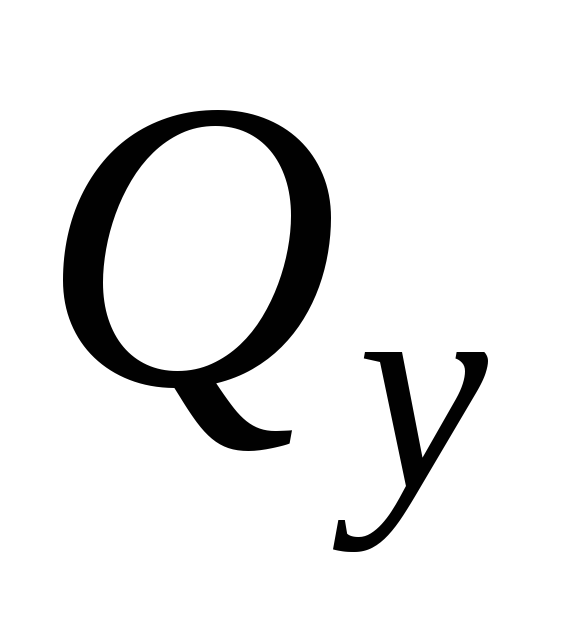или ), лежит в плоскости поперечного сечения, то и напряжения, лежат в плоскости сечения стержня. То есть при сдвиге в точках поперечного сечения стержня возникают только касательные напряжения .

Таким образом, поперечная сила, возникающая в сечении

. (4.1)

При сдвиге считают, что касательные напряжения равномерно распределены по площади поперечного сечения, т.е. , поэтому

(4.2)

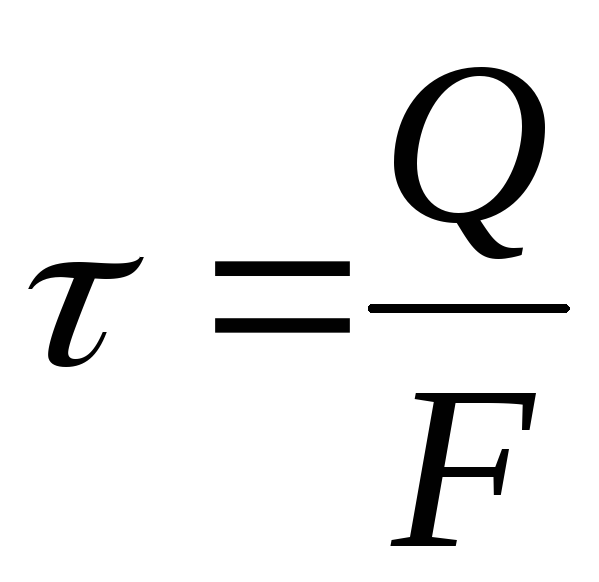
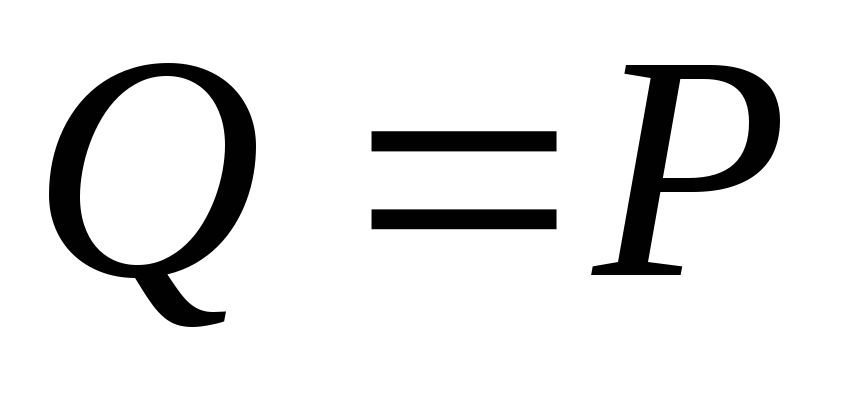
Касательные напряжения при сдвиге определяются по формуле , а так как, то

. (4.3)

4.2 Напряженное состояние при сдвиге

Чистый сдвиг – частный случай плоского напряженного состояния, при котором по граням прямоугольного элемента действуют только касательные напряжения.

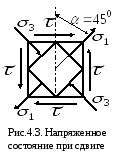
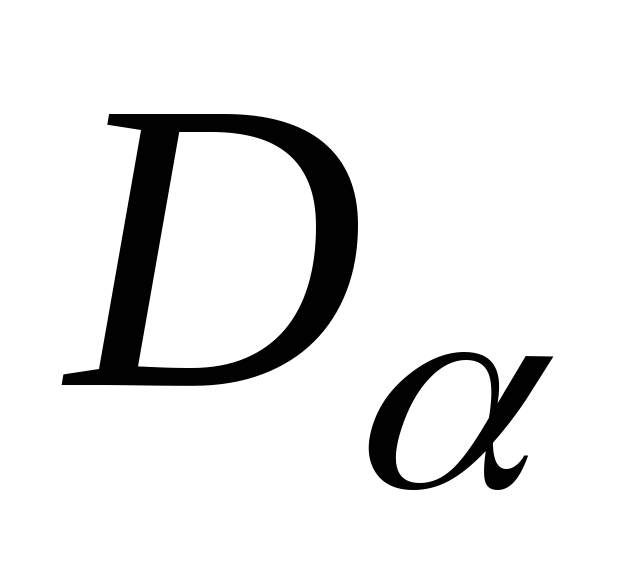
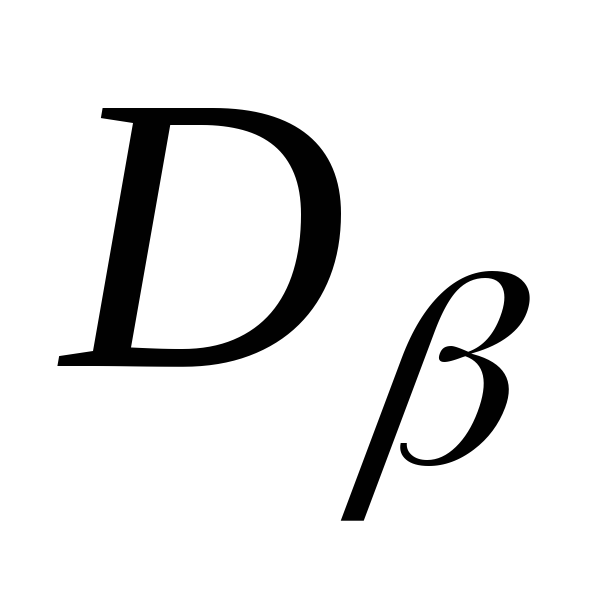
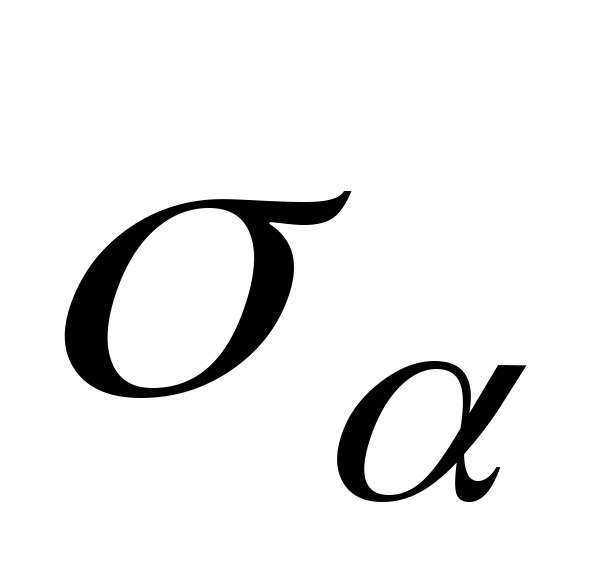
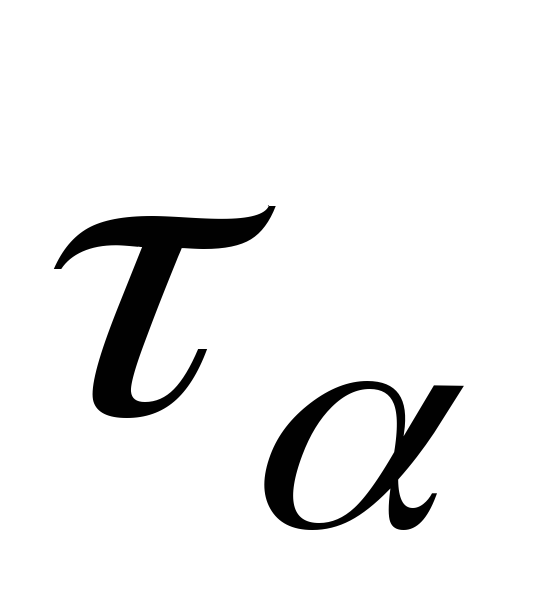
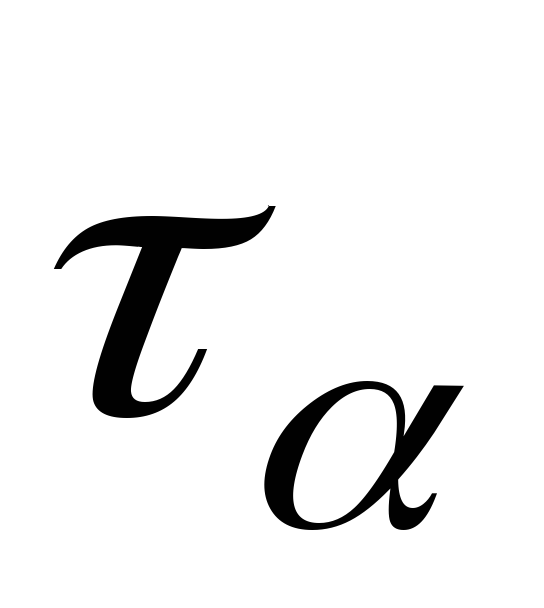
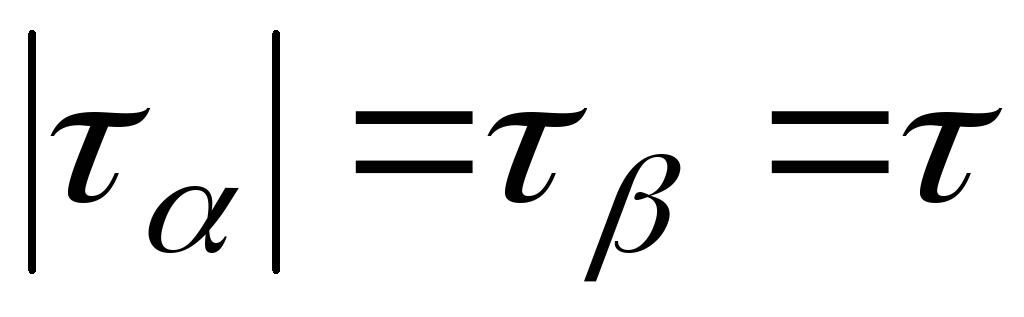
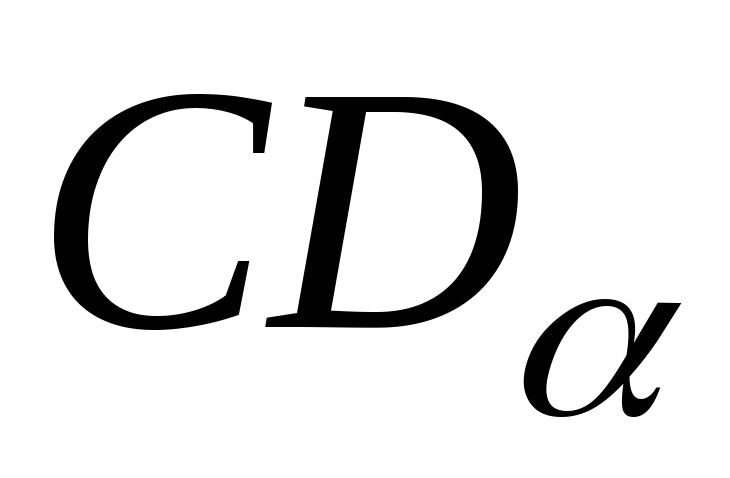
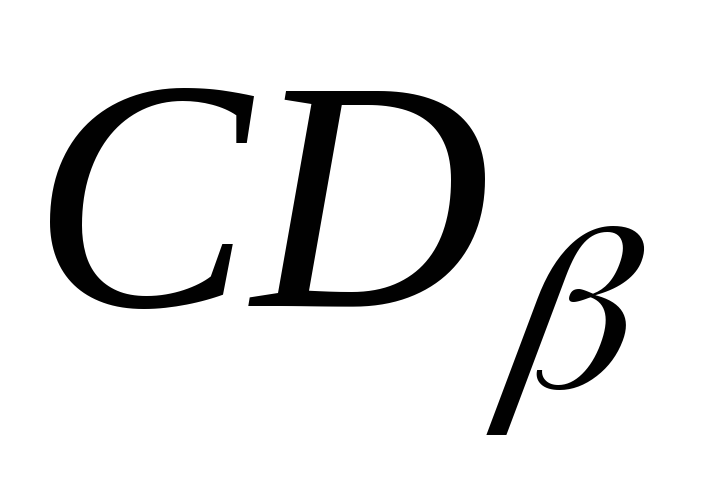
Построим круг Мора: Точкииточки, соответствующие напряженному состоянию на указанных взаимно перпендикулярных площадкахис координатами (;) т.е. (0; —) и (;) т.е. (0;) соответственно (). Через эти две точки проводится окружность радиусомили(точка С – центр круга Мора). В точках где круг Мора пересекает осьможно найти величину главных нормальных напряжений(так как касательные напряжения равны нулю.

Определим величину и направление главных напряжений при чистом сдвиге:

,(4.4)

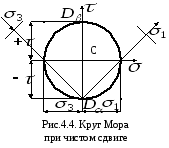
так как , можно записатьи

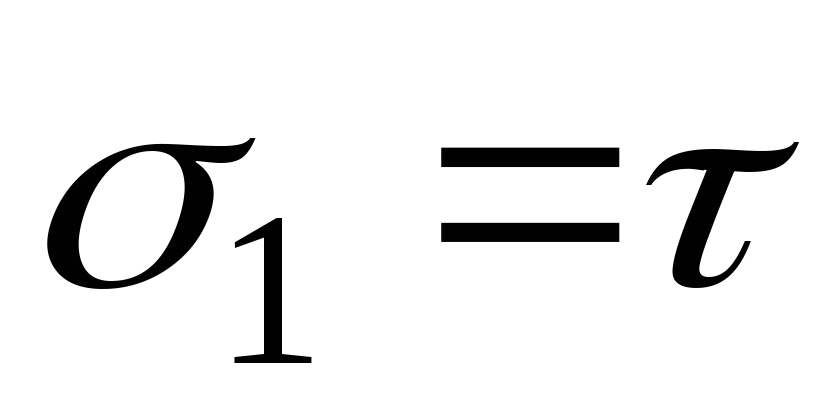
Направление главных площадок определяется углом , который найдем по формуле:

; (4.5)

учитывая что ,

;

; .

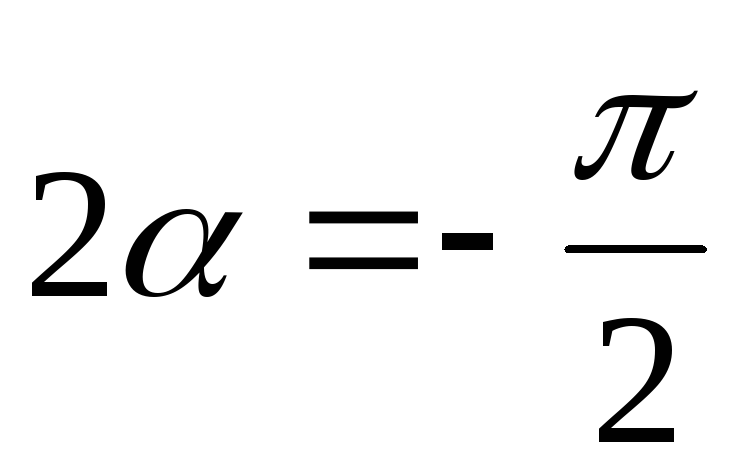
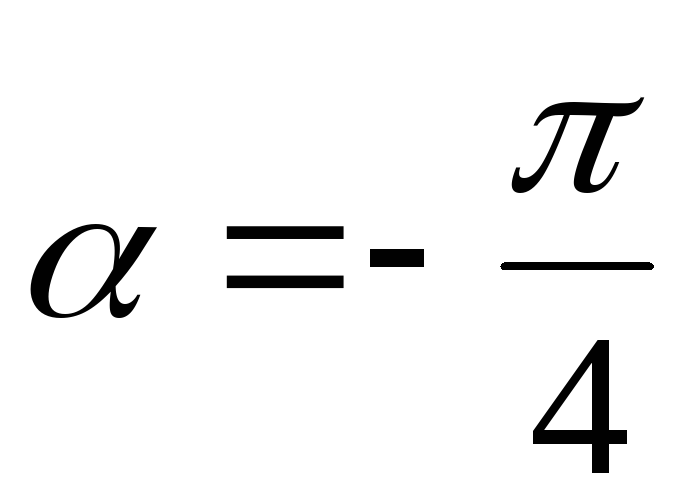
4.3 Деформации при сдвиге

Рассмотрим деформацию квадратного элемента при сдвиге.

Рис.4.5. Деформация квадратного элемента при сдвиге.

оскольку по граням элемента не действуют нормальные напряжения, то 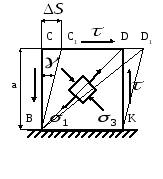вдоль граней нет и удлинений. В то же время диагональBD, совпадающая с направлением , удлинится, а диагональ СК, совпадающая с направлением сжимающего напряжения, укоротиться. В результате квадратBCDK трансформируется в ромб BC₁D₁K, без изменения длины граней. Таким образом, деформация сдвига характеризуется изменением первоначально прямых углов.

Малый угол , на который изменяется первоначально прямой угол элемента при сдвиге, называетсяуглом сдвига или относительным сдвигом.

Величину абсолютного смещения грани обозначают и называютабсолютным сдвигом.

Из прямоугольного треугольника ВСС₁:

(4.6)

Учитывая малость угла можно считать, что , тогда окончательно запишем взаимосвязь между относительным и абсолютным сдвигом элемента

(4.7)

При сдвиге можно экспериментально построить диаграмму сдвига, аналогичную диаграмме растяжения, на которой также в начале нагружения будет прямолинейный участок деформации по закону Гука.

Закон Гука при сдвиге:

или , (4.8)

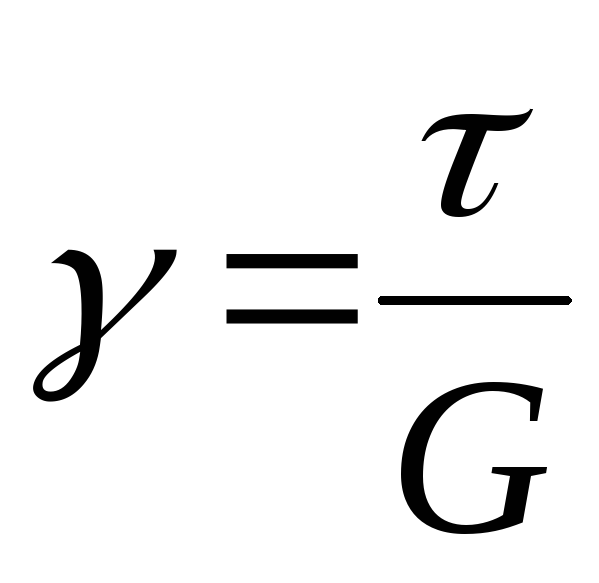
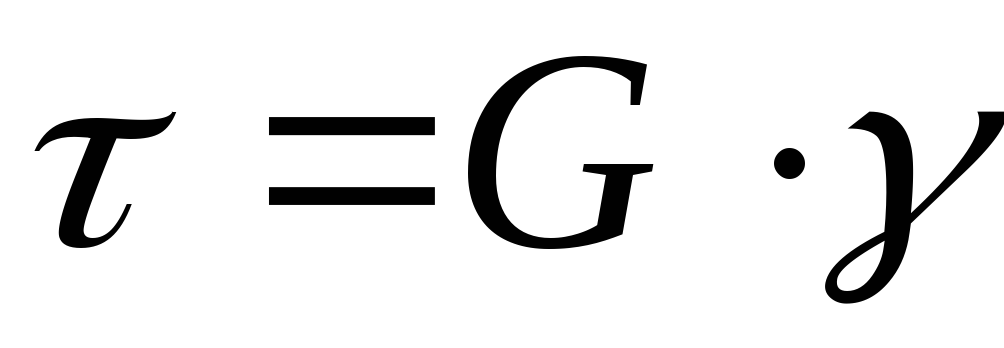
где G – модуль касательной упругости или модуль сдвига (модуль упругости второго рода), которая является константой для данного материала.

Закон Гука при сдвиге через абсолютные деформации:

, (4.9)

где а – расстояние между сдвигаемыми гранями; F – площадь грани.

Взаимосвязь между упругими постоянными:

. (4.10)

Источник