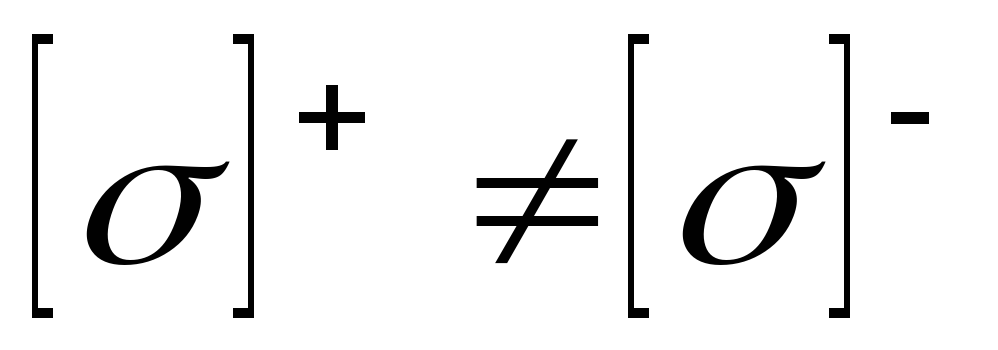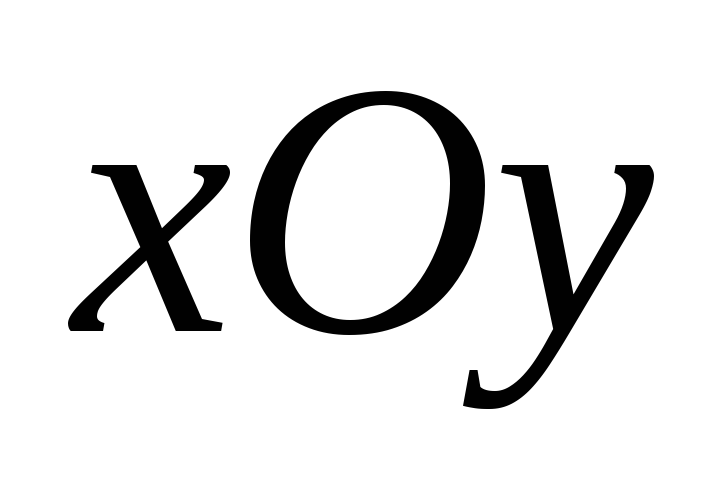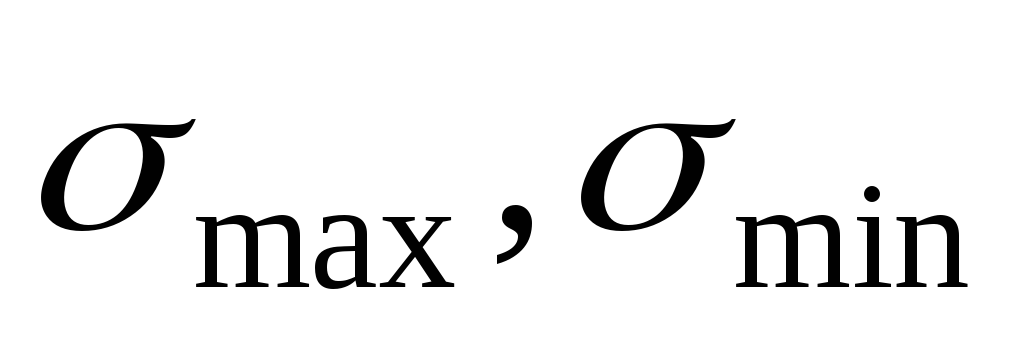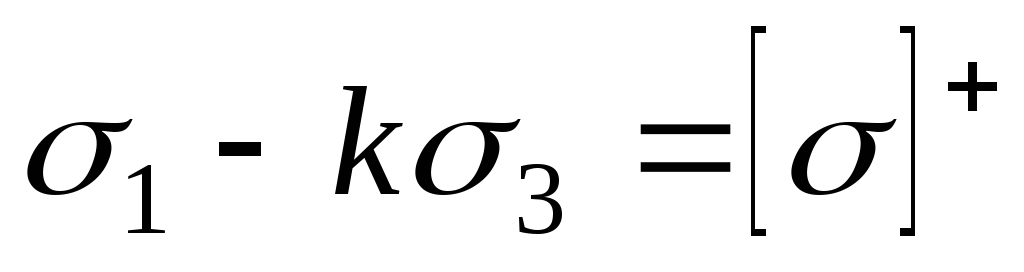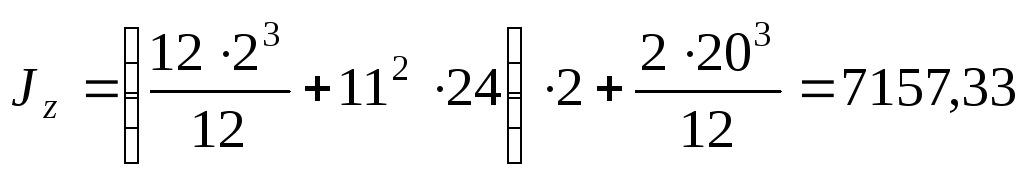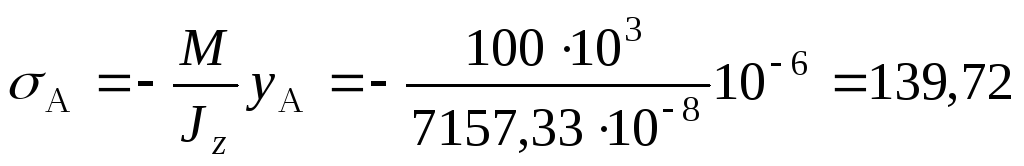Теория прочности мора эквивалентные напряжения

Билет 4

1.Теория напряжений. Круговая диаграмма о.Мора. Вывод формулы.

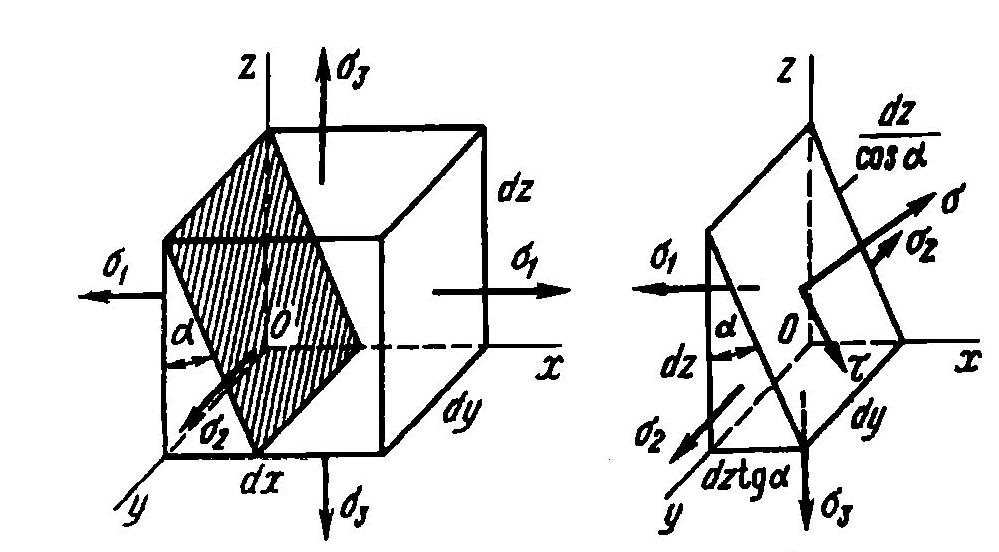
Рассмотрим условия равновесия треугольной призмы (рис). Она образована путем сечения элементарного параллелепипеда

наклонной площадкой, которая независимо от угла наклона αостается параллельной одной из главных осей(y)

П роецируя все силы, действующие на отсеченную призму, на оси параллельные векторам α и τ :

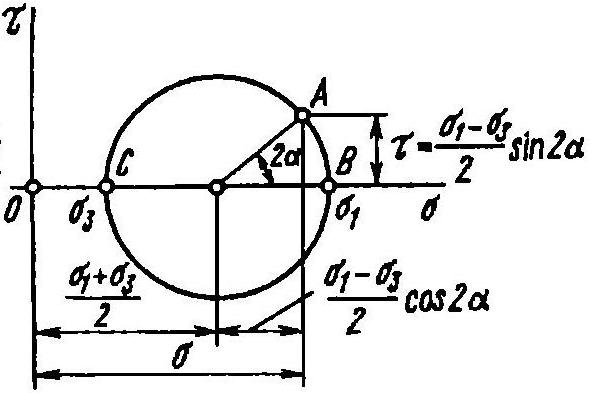
– напряжения в семействе площадок параллельных 1 из гл. осей, можно дать геом. толкование:

; в системе координат,τ это есть ур-ие окружности, центр которой находится на расстоянии ) от нач.координат.. Окружность построенная на отрезке как

на диаметре называется Круговой диаграммой О.Мора. ( ур-ие окр)

2. Учет симметрии при решении статически неопределимых стержневых систем. Показать на примерах.

Билет 5

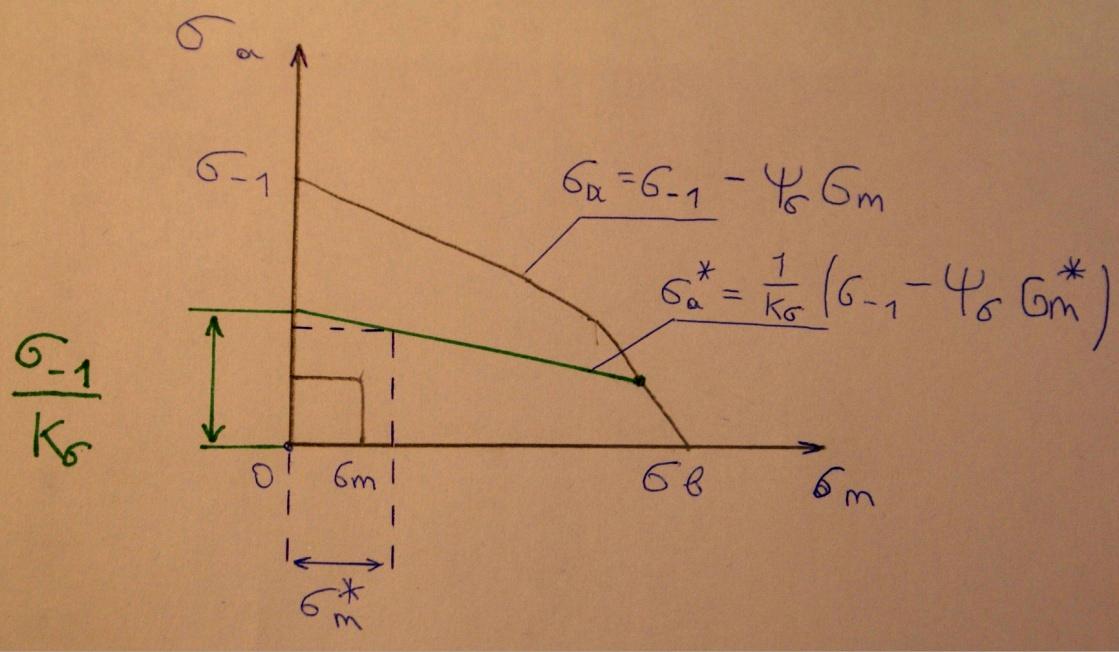
1. Расчеты на прочность при напряжениях, переменных во времени

Большинство деталей в различных машинах подвергаются действию циклически изменяющихся напряжений.

При циклическом изменении напряжений поломка деталей может происходить при напряжениях, значительно меньших, чем предел текучести.

Цикл- совокупность напряжений за период времени.

Циклы с одинаковыми R называются подобными.

Определение коэффициента запаса по выносливости при одноосном напряженном состоянии.

Все полученный формулы применимы только при регулярном нагружении, при котором амплитуда и не меняются.

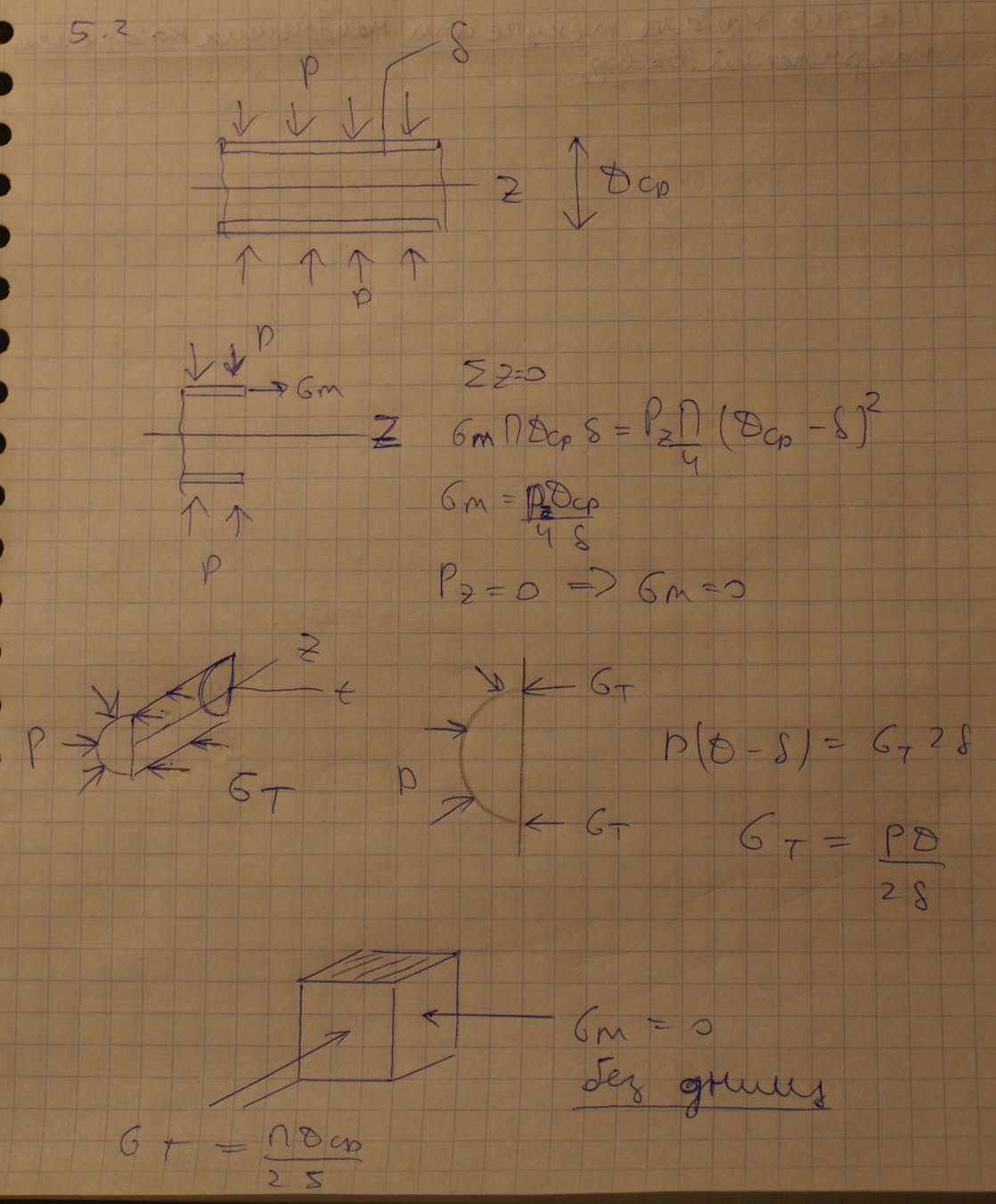
2.Напряжения, возникающие в тонкостенной трубке без днищ, нагруженной внешним давлением.

Билет 6

1. Теория начала текучести наибольших касательных напряжений. Вывод.

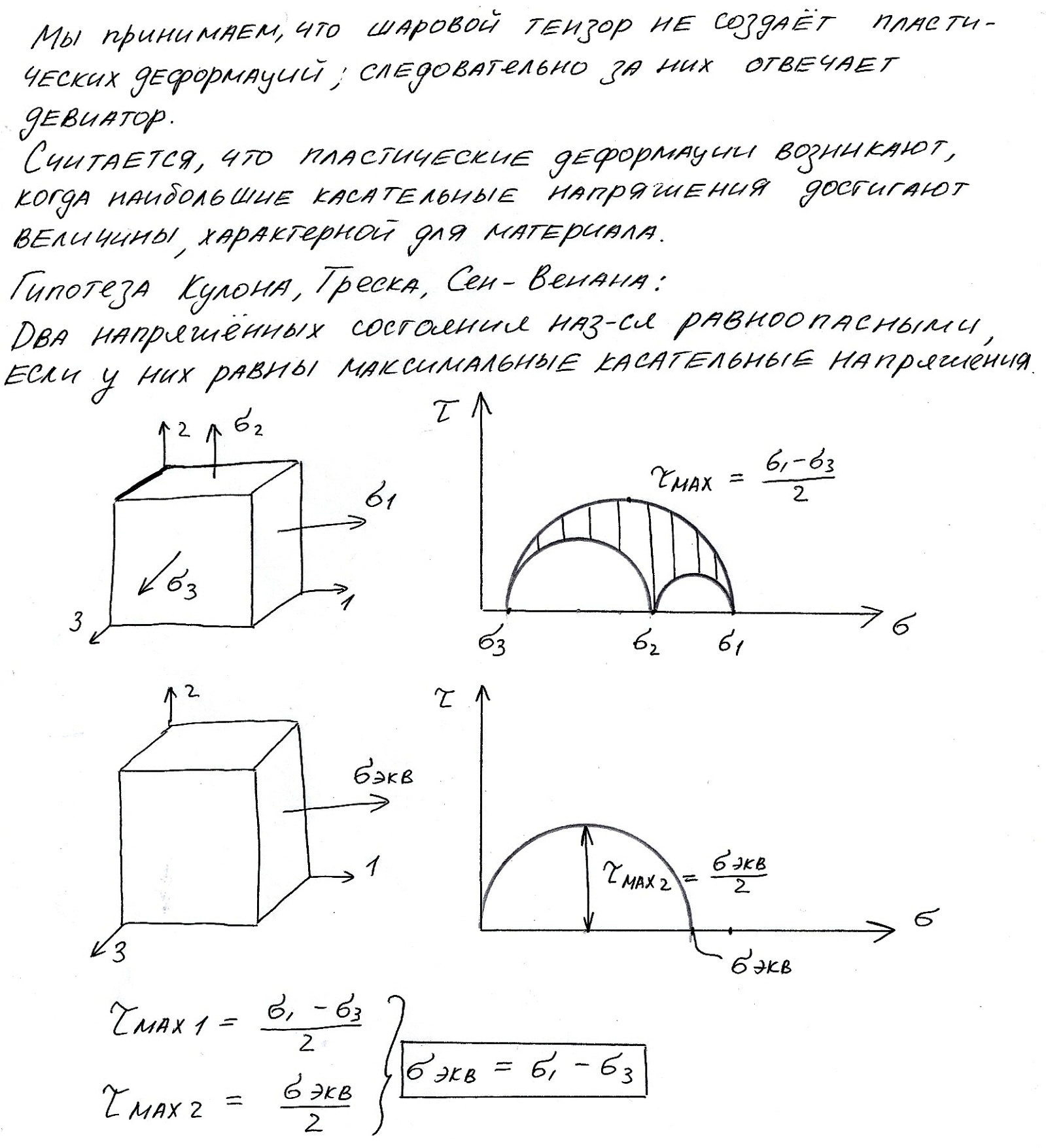
Мы принимаем, что шаровой тензор не создаёт пластических деформаций; следовательно за них отвечает девиатор.

Считается, что пластические деформации возникают, когда наибольшие касательные напряжения достигают величины, характерной для материала.

Гипотеза Кулона, Треска, Сен-Венана:

Два напряженных состояния называются равноопасными, если у них равны максимальные касательные напряжения.

2. Определение перемещений в статически неопределимых стержневых системах

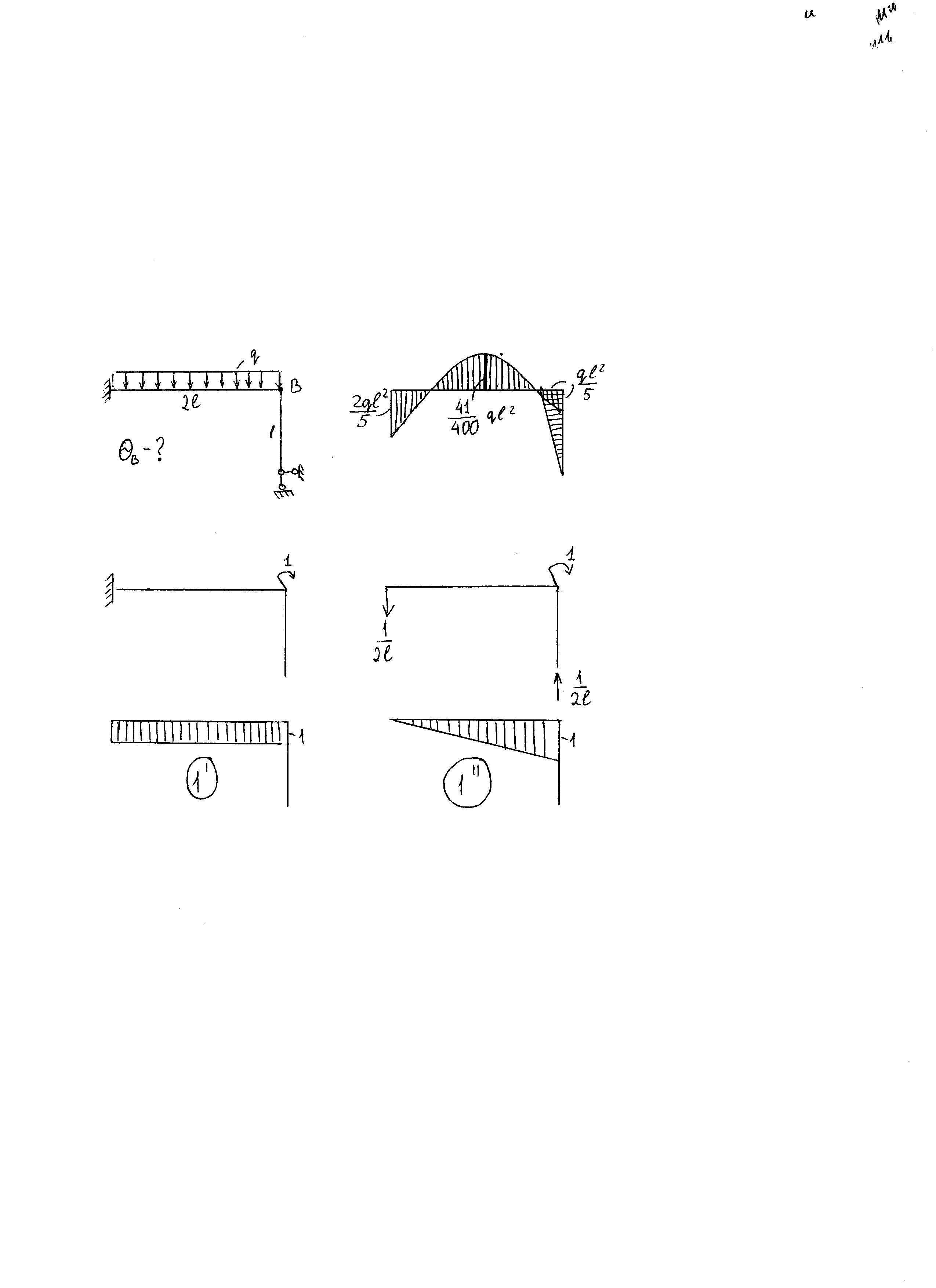
Перемещение ищем после того, как раскрыта статическая неопределённость и построена суммарная эпюра моментов.

Чтобы ещё раз не раскрывать статическую неопределённость, перемещение будем искать не для заданной системы, а для эквивалентной.

Для этого берём любую эквивалентную систему, разгружаем область внешних сил и, согласно интегралам Мора, прикладываем единичный фактор в направлении искомого перемещения.

После перемножаем суммарную эпюру М с эпюрой единичного фактора, используя графоаналитический способ взятия интегралов Мора.

Рассмотрим 2 эквивалентные системы:

Как видно, получили одинаковые результаты, т.е. от выбора эквивалентной системы ничего не зависит.

Источник

5. Теория прочности Мора

Рассмотренные выше теории, основанные на проверке прочности для пластичных материалов по величине касательных напряжений, не учитывают различие свойств материала при работе на растяжения и сжатие, т.е. для случаев, когда . Такое различие свойств материалов учитывается теорией, получившей имя немецкого ученого Мора. Эта теория, являясь дополнением к третьей теории прочности, имеет довольно громоздкий вид. Это связано с тем, что при ее получении напряженное состояние описывалось графическим образом с помощью так называемых кругов Мора.

Рассмотрим другой способ, основанный на обобщении теории наибольших касательных напряжений. В соответствии с этой теорией условие прочности имеет вид (10.19). Перепишем это уравнение следующим образом:

. (10.24)

Уравнение (10.24) в графическом смысле представляет собой прямую линию, где ;; при; при.

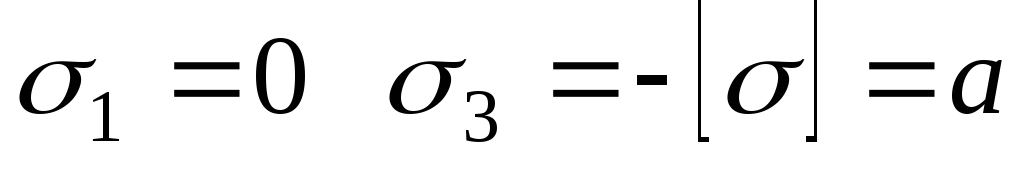
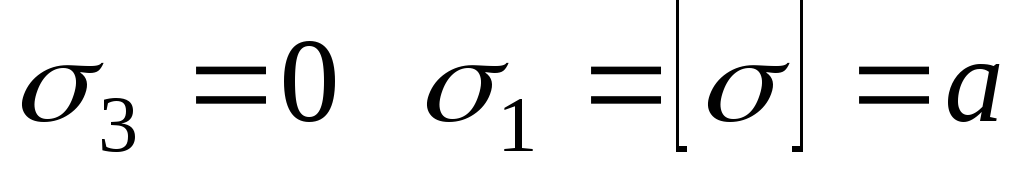
. (10.25)

Вид этой прямой приведен на рис.10.6,а.

Любая точка, принадлежащая плоскости , например, точка А, отвечает определенному напряженному состоянию. Прямая (10.25) делит эту плоскость на три зоны: зона предельных напряженных состояний – точки этой зоны лежат на предельной прямой линии (10.25); зона безопасных напряженных состяний точки этой зоны лежат выше и левее предельной прямой (внутренняя область); зона опасных напряженных состояний – точки этой зоны лежат правее и ниже предельной прямой (внешняя область). В точках этой области гарантировать прочность нельзя.

Таким образом, приведенный на рис.10.6,а график дает возможность оценить с помощью третьей теории прочность элемента по местонахождению точки, определяющей данное напряженное состояние ().

Используя аналогию, рассмотрим случай, когда . В этом случае точки предельной прямой, принадлежащие осям координат определяют следующие напряженные состояния:;.

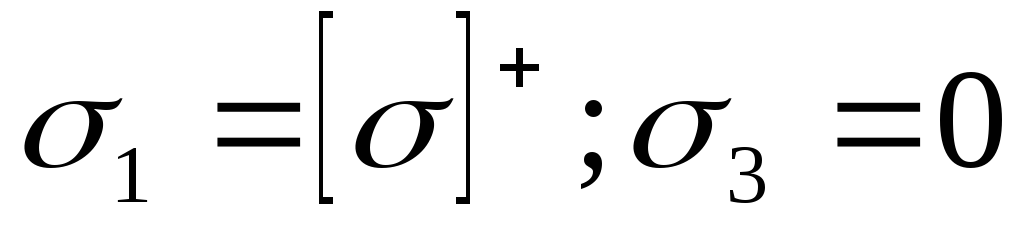
Вид предельной прямой для этого случая приведен на рис.10.6,б. Опишем эту прямую.

Уравнение прямой в отрезках имеет вид:

. (10.26)

Здесь: ;;;.

Введем коэффициент , подставим в уравнение (10.26) и преобразуем его к виду:

. (10.27)

Уравнение (10.27) является уравнением предельной прямой. Левая часть этого уравнения представляет собой эквивалентные напряжения для рассматриваемого напряженного состояния. Вводя знак неравенства в уравнение предельной прямой (10.27), получаем теорию прочности Мора:

. (10.28)

Неравенство (10.28) описывает внутреннюю область безопасных напряжений (Рис.10.6,б).

Теория прочности Мора является обобщением теории наибольших касательных напряжений и будет ей идентичной при равенстве допускаемых напряжений . В этом случае коэффициент.

Пятая теория (теория прочности Мора) прочности хорошо подтверждается опытом для большинства строительных материалов (камень, дерево, пластмассы), т.е. для тех материалов, которые не укладываются в сформулированные ранее классические теории прочности.

Подводя итог рассмотрению классических теорий прочности, можно написать условие прочности при объемном напряженном состоянии в таком виде:

, (10.29)

где эквивалентное (расчетное) напряжение;допускаемое напряжение при простом растяжении и сжатии. Расчетное напряженное состояниеможет быть истолковано как растягивающее напряжение при линейном напряженном состоянии, эквивалентном рассматриваемому сложному напряженному состоянию в отношении опасности для прочности материала.

Выбор теории прочности, а значит и формулы для , таким образом, отвечает на вопрос: какой критерий прочности материала столь же надежен для рассматриваемого объемного напряженного состояния, как и для линейного?

Что касается практического применения теорий прочности, то здесь следует иметь ввиду, что любой материал в зависимости от условий работы и вида напряженного состояния может находиться и в хрупком и в пластичном состоянии. В связи с этим следует выделить те теории прочности, пригодные для проверки прочности материала при его пластическом состоянии, и те, которые следует применять для проверки прочности материалов в хрупком состоянии. Эксперименты показывают, что для пластичного состояния матерала наиболее достоверной является энергетическая теория прочности. Незначительно расходится с опытами для пластичных материалов теория наибольших касательных напряжений.

Что касается хрупкого состояния материалов, то для оценки прочности в этом случае иногда используется вторая теория прочности теория наибольших линейных деформаций; имеются опыты, которые показывают, что в ряде случаев подтверждается для такого состояния материала и теория наибольших нормальных напряжений; ею пользуются на практике для проверки прочности таких материалов как камень, чугун и т.д.

Кроме классичесих теорий прочности, рассмотренных в данной теме, существует еще несколько десятков так называемых “новых”теорий, предлагающих новые подходы к оценке прочности конструкционных материалов. В рамках настоящего пособия эти теории не приводятся. Тех, кого эта проблема интересует, может обратиться к специальной литературе учебного или справочного характера, часть из которой приводится в конце пособия.

Все приведенные выше теории прочности были записаны через главные напряжения. В практике мы часто имеем дело не с главными напряжениями. В связи с этим при практических расчетах удобно иметь формулы для эквивалентных напряжений для различных теорий прочности, выраженные через нормальные и касательные напряжения, действующие в произвольных площадках.

Рассмотрим несколько частных случаев плоского напряженного состояния и запишем для этих случаев условия прочности в соответствии с различными теориями.

Одним из таких частных видов напряженного состояния приведен на рис.10.7. Этот вид напряженного состояния часто встречается в расчетной практике при плоском поперечном изгибе, некоторых видах сложного сопротивления и т.д.

При записи эквивалентных напряжений для приведенного на рис.10.7 частного вида напряженного состояния примем во внимание, что

. (10.30)

Подставляя (10.30) в выражение (10.17), условие прочности в соответствии с первой теорией прочности получим в виде:

. (10.31)

Для второй теории выражение для условия прочности после подстановки (10.30) в (10.18) принимает вид:

. (10.32)

Для третьей теории условие прочности после подстановки (10.30) в (10.19) запишется так:

. (10.33)

По четвертой теории условие прочности после подстаноки (10.30) в (10.23) и некоторых преобразований будет иметь вид:

. (10.34)

Как уже отмечалось выше, для оценки прочности пластичных материалов используют как теорию наибольших касательных напряжений, так и энергетическую теорию прочности. Выясним на примере рассматриваемого выше частного случая напряженного состояния, каково расхождение между этими теориями прочности. Для этого, используя выражения (10.33) и (10.34), вычислим значения эквивалентных напряжений при различных исходных значениях и.

Пусть . Тогда. При;. Сравнивая эти значения, приходим к выводу, что максимальное расхождение между третьей и четвертой теориями составляет 15%. В практических задачах при небольших значениях касательных напряжений это расхождение существенно меньше. Поэтому используют обе теории для оценки прочности материалов в пластическом состоянии.

Пример 10.1.Исследовать напряженное состяние в стенке стального сварного двутавра в месте перехода от полки к стенке (в точке А) и выполнить проверку прочности балки, используя четвертую теорию прочности. В рассматриваемом сечении балки изгибающий момент равенкНм, поперечная силакН. Поперечное сечение балки приведено на рис.10.8а.

1. Найдем момент инерции двутавра относительной оси в (см 4 ).

см 4 .

2. Определяем нормальные напряжения в точке А:

МПа.

3. Определяем касательные напряжения в точке А поперчного сечения:

МПа.

4. Вычисляем эквивалентное напряжение в точке А, используя четвертую теорию прочности. Напряженное состояние в точке А – плоское (Рис.10.8,б). Для частного случая напряженного состояния, приведенного на рис.10.8,б эквивалентное напряжение по четвертой теории равно:

МПа.

5. Сравниваем расчетное напряжение с допускаемым для стали МПа, используя условие прочности (10.34). Расчетное напряжениеМПа оказалось меньше допускаемого. Следовательно, напряженное состояние в точке А поперечного сечения балки является безопасным.

Пример 10.2.Проверить прочность чугунной детали (работающей на сложное напряженное состояние), если главные напряжения в опасной точке сечения:МПа;;МПа. Коэффициент Пуассона.

Допускаемое напряжение на растяжение МПа, допускаемое напряжение на сжатиеМПа.

1. Для проверки прочности чугуна на растяжение следует применить теорию наибольших линейных деформаций:

МПа.

Полученное расчетное напряжение блитзко к допускаемому на растяжение.

2. Если бы мы воспользовались для расчета теорией наибольших касательных напряжений (неприменимой для хрупкого состояния материала), то получили бы ошибочные результаты:

МПа.

В этом случае расчетное напряжение оказывается близким к разрушающему напряжению.

Источник