Теория прочности кулона мора сопромат

11. Сопротивление сдвигу при сложном напряженном состоянии. Теория прочности кулона – мора

Изученная нами схема одноплоскостного сдвига соответствует частным случаям разрушения грунта в основании сооружения. Более точно этот процесс можно представить, рассмотрев прочность грунта в условиях сложного напряженного состояния.

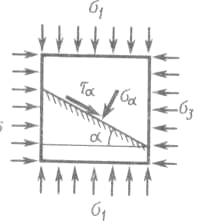
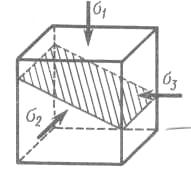
Пусть к граням элементарного объема (рис. 14, а) приложены главные напряжения σ₁ > σ₂ > σ_3. Если постепенно увеличивать напряжение σ_1, оставляя постоянной величину σ₃, то в соответствии с теорией Кулона-Мора произойдет сдвиг по некоторой наклонной площадке, причем промежуточное главное напряжение σ₂ никак не влияет на сопротивление грунта сдвигу (рис. 14, б).

Как уже известно, на площадке сдвига выполнено условие:

τ = σ_i · tgφ + с

а б

Рис. 14. К определению прочности грунта в условиях сложного

а — положение наклонной площадки скольжения; б — распределение напряжений на площадке сдвига

Из курса сопротивления материалов известно, что для площадки, расположенной под углом α, напряжения равны:

Тогда закон сопротивления сдвигу на этой площадке можно записать в виде

Подставим в это уравнение выражение (46) и продифференцируем, получим выражение

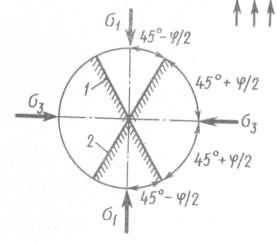
Отсюда следует, что в предельном состоянии в каждой точке грунта имеется две сопряженные площадки скольжения (рис. 15), действующие под углами

Рис. 15. Ориентация площадок скольжения относительно

направления действия главных напряжений

12. Деформируемость грунтов

При статистической нагрузке, если она превысит прочность структурных связей грунта, возникают упругие и остаточные деформации (см. п.6). Особенностью грунтов является то, что при внешней нагрузке отдельные элементы грунтов по-разному оказывают сопротивление внешним нагрузкам и по-разному деформируются. Соответственно по-разному ведут себя сыпучие и связные грунты.

В сыпучих (несвязных) грунтах при нагружении всегда возникают необратимые смещения и повороты зерен грунта относительно друг друга. Это приводит к образованию остаточных деформаций.

В связных грунтах на характер деформирования влияют структурные связи. При жестких (кристаллизационных) связях, если нагрузка такова, что прочность связей не нарушается, то грунт деформируется как упругое твердое тело. При вязких (вводно-коллоидных) связях некоторые связи начинают разрушаться (или вязко течь) уже при малых нагрузках, что и определяет при разгрузке наличие не только обратимых, но и остаточных деформаций.

Упругие деформации складываются из сжатия пузырьков воздуха в порох, изменение толщины пленки воды и некоторых упругих деформаций зерен грунта. При снятии нагрузки мгновенно исчезают упругие деформации зерен, а через некоторое время — деформации пузырьков воздуха и водных пленок.

Остаточные деформации возникают от необратимых отжатий воды и воздуха из-под грунта и взаимных необратимых перемещений зерен грунта. Под штампом или фундаментом остается уплотненное грунтовое основание.

Упругие деформации распространяются в стороны, а остаточные — только под штампом, причем последние приводят к выдавливаю грунта.

Очевидно, что при увеличении напряжений увеличиваются и деформации, следовательно, между деформациями и напряжениями существует зависимость: . Зависимость эта сложна, так как грунт весьма разнообразен (по связям). В общем случае эта зависимость нелинейная и на базе проведенных экспериментов (рис. 16) выглядит так:

где а_с а_n и — коэффициенты эмпирические; σ_c — напряжения, не превосходящие прочности структурных связей; σ_n — напряжения, нарушающие структурные связи; m — параметр нелинейности (экспериментальный).

Рис. 16. Экспериментальная зависимость между напряжениями

Но для практических инженерных решений (на рис. 16 промежуток ) между общими деформациями и напряжением при постоянстве принимают

При небольших изменениях нагрузок грунты рассматривают как линейно деформируемые тела. Для определения напряжений можно применять решения теории упругости.

Источник

1.8 Критерий Кулона-Мора

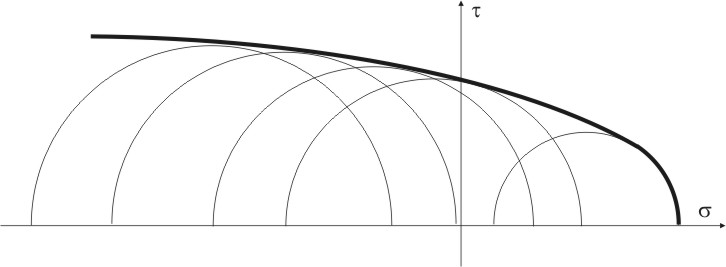
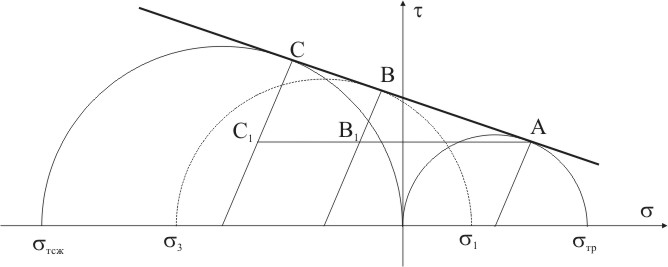
Рассмотренные критерии пластичности применимы для материалов одинаково сопротивляющихся растяжению и сжатию. Однако, ряд материалов обладает разной прочностью при растяжении и сжатии. Критерий Кулона-Мора основан на предположении, что прочность зависит, главным образом, от величины и знака наибольшего ₁ и наименьшего₃ главных напряжений. Если при некоторых ₁ и ₃ возникает текучесть, то круг Мора, построенный на этих напряжениях, соответствует предельному состоянию материала. Меняя соотношение между ₁ и ₃, получим семейство предельных кругов. Огибающая этих кругов определяет сочетания нормальных и касательных напряжений, при которых возникает текучесть материала (рис 9.4).

Для точного построения огибающей необходимо выполнить большое количество экспериментов при различных напряженных состояниях. На практике ограничиваются минимальным количеством испытаний для наиболее просто реализуемых напряженных состояний. Огибающую можно с достаточной степенью точностью заменить прямой касательной к кругам Мора построенным для растяжения с диаметром равным пределу текучести при растяжении _{т р} и для сжатия — с диаметром равным пределу текучести при сжатии _{т сж}. Следовательно, для построения схематизированной огибающей достаточно провести испытания образцов материала при одноосном растяжении и при одноосном сжатии. С достаточной степенью точности огибающая заменяется касательной к кругам Мора, соответствующих результатам этих испытаний (рис. 9.5).

Это позволяет найти зависимость между главными напряжениями рассматриваемого напряженного состояния ₁ и ₃ и эквивалентным напряжением _экв при равноопасном одноосном растяжении. В точка касания огибающей с тремя кругами восстановим перпендикуляры, которые совпадают с радиусами кругов, а через точку А проведем горизонтальную прямую. Из подобия треугольников ABB₁ и ACC₁, следует

Подставим эти выражения в соотношение (1) и после преобразований получим условие тукучести:

Обозначим , тогда условие текучести принимает вид:

Следовательно, эквивалентное напряжение:

При двухосном напряженном состоянии σ₃ = 0, следовательно, условие текучести принимает вид:

Учитывая, что для бруса в опасном сечении действуют нормальные напряжения σ и касательные напряжения τ_max, тогда главные напряжения:

Подставим выражение (3) в соотношение (2) после преобразований получим условие текучести для бруса:

Эквивалентное напряжение для бруса:

1.9 Условия текучести при двухосном напряженном состоянии

Проанализируем условия текучести при различных критериях для двуосного напряженного состояния. Условия текучести имеют следующий вид:

а) по критерию максимального главного напряжения:

б) по критерию максимальной главной деформации:

в) по критерию суммарной энергии деформации:

σ₁ 2 + σ₂ 2 + 2μσ₁σ₂ = σ_тр 2

г) по критерию максимальных касательных напряжений:

д) по критериям энергии деформации сдвига и интенсивности напряжений:

Представим эти соотношения в прямоугольных координатах «u-v», которые повернуты относительно координат «σ₁-σ₂» на 45 против часовой стрелки. Для этого подставим в условия текучести:

Тогда при различных критериях для двуосного напряженного состояния и при равенстве пределов текучести на растяжение и сжатие (σ_тр = σ_тсж = σ_т) условия текучести принимают вид.

а) по критерию максимального главного напряжения:

б) по критерию максимальной главной деформации:

в) по критерию суммарной энергии деформации:

Это уравнение эллипса с центром в начале координат, малой полуосью и большой полуосью ;

г) по критерию максимальных касательных напряжений:

д) по критерию энергии деформации сдвига и интенсивности напряжений:

Это уравнение эллипса с центром в начале координат, малой полуосью и большой полуосью .

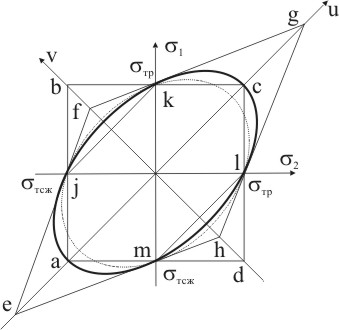
Построим приведенные соотношения в прямоугольных координатах «σ₁-σ₂» (рис. 9.6).

Фигура Критерий статической прочности

abcd Критерий максимального главного напряжения

efgh Критерий максимальной главной деформации

ajkclm Критерий максимальных касательных напряжений

эллипс (сплошная линия) Критерий энергии деформации сдвигу

эллипс (пунктирная линия) Критерий суммарной энергии деформации

Каждая из фигур означает, что для соответствующего критерия текучесть не наступит до тех пор, пока точка со значениями σ₁, σ₂ не выйдет за пределы области ограниченной фигурой. Сравнение областей ограниченных различными фигурами показывает, что наименьшая область ограничена шестиугольником ajkclm, который соответствует критерию максимальных касательных напряжений. Можно заметить, что в том случае, когда главные напряжения σ₁, и σ₂ одновременно растягивающие или сжимающие, то области ограниченные шестиугольником ajkclm и квадратом abcd ( 1-ая и 3-ая четверти прямоугольной системы координат) совпадают. В том случае, когда одно из главных напряжений растягивающее, а другое сжимающее, то область, ограниченная шестиугольником ajkclm меньше области ограниченной квадратом abcd. Это означает, что при прогнозе текучести по критерию максимальных касательных напряжений текучесть наступит раньше, чем по критерию наибольших главных напряжений. Эллипс, ограничивающий область соответствующую, как критерию энергии деформации сдвига, так и критерию интенсивности напряжений огибает шестигранник, соответствующий критерию наибольших касательных напряжений. Таким образом, по критерию энергии деформации сдвига текучесть наступит при больших значениях главных напряжений σ₁, и σ₂, чем по критерию наибольших касательных напряжений. По критерию максимальной главной деформации область ограничена ромбом диагонали которого совпадают с осями координат u-v, развернутыми относительно исходной системы координат σ₁-σ₂ на 45.

В заключении следует отметить, что прогноз текучести по шести рассмотренным критериям предельного состояния только по трем критериям (критерий наибольших касательных напряжений, критерий энергии сдвига и критерий интенсивности напряжений) согласуются с результатами эксперимента. Кроме того только эти три критерия позволяют утверждать, что текучесть не наступит при всестороннем растяжении или сжатии в условиях отсутствия касательных напряжений, что также подтверждается экспериментом.

Источник

Теория прочности Кулона-Мора

В теории Мора в отличие от выше изложенных теорий, не закладывается отдельный критерий, а на основе эксперимента устанавливается определенная зависимость прочностных свойств материала от вида напряженного состояния. Для объяснения этой зависимости используются круги напряжения (круги Мора).

Опыты показывают, что ошибка из-за не учета не превышает 10—15%. Поэтому влиянием пренебрегают. На основе опытов строятся круги напряжений и предельная огибающая.

Критерий прочности формулируется следующим образом:

Причиной разрушения материала по теории Мора является достижение такого состояния, когда круг напряжений, соответствующий напряженному состоянию, выходит за пределы огибающей.

В практике расчетов огибающую заменяют прямой. Тогда условие наступления предельного состояния принимает вид:

• — соответственно, предельное напряжение при растяжении и при сжатии;
• K — коэффициент, равный отношению:

Предельные круги напряжений и предельная огибающая

Теория Мора дает наиболее достоверные результаты для напряженных состояний, круги которых занимают промежуточное положение между предельным кругом сжатия и предельным кругом растяжения.

Источник