Теория начала текучести мора

Билет № 22

1) Теория начала текучести энергии изменения формы.

Два напряженных состояния считаются равноопасными, если удельная энергия изменения формы у них одинаковая.

Пластические деформации возникают, когда энергия формоизменения достиг части какой либо определенной величины

Для эквивалентного напряженного состояния

Упрощенное напряженное состояние

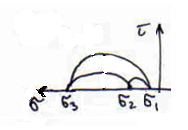
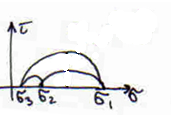
Для сравнения двух теорий можно воспользоваться испытаниями на кручение (изобразить чистый сдвиг. ):

τ_т= ~0,57σ_т — более точные результаты

2) Методы проверки расчета статически неопределимых стержневых систем:

1. Выбрать эквивалентную основную систему и заново раскрыть статическую неопределимость (заново решить задачу от начала до конца)
2. Определить перемещения в различных основных системах (в различных 2х о.с.)
3. Суммарную эпюру перемножают на единичную эпюру любой другой основной системы, в итоге должен получиться ноль. Нельзя перемножать на ед. эпюру другой основной системы, если эта эпюра совпадает по виду с ед. эпюрой, которую использовали при раскрытии статической неопределимости.
4. Для статически неопределимых балок: дифференциальное уравнение упругой линии; константы ищутся из двух граничных условий, а третье граничное условие используется для проверки.

Б илет 23

1)Устойчивость продольно сжатых стержней. Пределы применимости

формулы Эйлера. Определение критических напряжений для стержней малой гибкости.

Устойчивость – свойство системы сохранять своё состояние при внешних воздействиях. Пусть стержню сообщили отклонение от положения равновесия. Если после устранения причин, вызвавших отклонение, система возвращается в исходное состояние равновесия, то положение считается устойчивым, если нет, то положение считается неустойчивым (рис)

Ф-ла Эйлера применима до — предел пропорциональности

2) Влияние качества обработки и состояния поверхности на усталостную прочность.

Виды обработки, влияющие на усталостную просность: механическая, специальная, химическая (тема не раскрывалась на лекции).

1) Механическая обработка: чем более гладкую пов-ть имеем, тем меньше вер-ть возникновения трещины усталостная прочность выше. Влияние чистоты пов-ти на предел выносливости отражает коэф-т:

г де — предел выносливости образца с типом обработки как у детали, — предел выносливости образца с тщательно отшлифованной пов-тью.

Предел выносливости – наибольшее напрежение, которое выдерживает образец сколь угодно долго не разрушаясь.

Зависимость для различных типов обработки (рис.):

2) Спец. виды обработки. Производятся для упрочнения поверхностного слоя детали.

К спец. видам относятся: наклёп пов-ного слоя путём обдувки дробью, накатки роликом, цементация.

Влияние технологических факторов на усталостную прочность оценивается коэф-том пов-ного упрочнения:

где — предел выносливости образца с типом спец. обработки как у детали.

Источник

5.3 Теория Мора.

В этой теории предполагается, что материал будет разрушен или неограниченно деформироваться. Когда касательное напряжение в плоскости разрушения достигнет определённой величины, зависящей от нормального напряжения , действующего в этой плоскости или когда наибольшее по абсолютной величине растягивающее главное напряжение достигнет величины .

Функциональная зависимость определяется для данного материала экспериментально. Эта зависимость является огибающей кругов Мора для данных значений σ_1,σ₃, при разрушении. Если круг Мора касается огибающей,

то материал будет разрушаться по плоскости, наклонённой под углом θ к направлению максимального главного напряжения. Таким образом, эта теория характеризует предельное максимальное напряжение и показывает плоскость, по которой будет происходить разрушение. Эта теория также не справедлива для растягивающих напряжений. Существует ещё целый ряд теорий, основанных на достижение определённых предельных значений комбинаций главных и касательных напряжений.

5.4 Критерий пластического течения.

Отметим два известных критерия начала пластического течения. Критерий начала пластического течения при сложном напряженном состоянии даётся некоторой функцией компонент напряжений, величина которого в момент начала течения достигает предела текучести при одноосном растяжении. Чаще всего используется выражение для эквивалентного напряжения, соответствующее критерию Мора

Критерий начала пластического течения формулируется как θ=σ_r, где σ_r -предел текучести при растяжении.

Физическим условием пластичности соответствует эквивалентное напряжение в другой форме — максимальное касательное напряжение (половина разности наибольшего и наименьшего главных напряжений):

Течение возникает, когда эквивалентное касательное напряжение достигает величины предела текучести при чистом сдвиге К.

τ=- К — критерий Треска или Треска — Сен — Венана.

Этот критерий лучше описывает поведение мягких сталей, обнаруживающих площадку текучести.

Упрочнения при пластической деформации можно объяснить как введение дополнительной работы на деформации.

Существует ряд других критериев перехода на пластичность, в том числе и эмпирических, в которых кроме упомянутых выше пределов текучести вводятся эмпирические коэффициенты. Между тем, сжатие материала и возникающие при этом дислокации и пластическое течение является не единственными и даже не определёнными причинами разрушения горных пород. Как уже упоминалось ранее, все приведенные выше критерии хрупкого разрушения и перехода к пластичности описывают поведение материалов при сжатии. При растяжении эти критерии как правило плохо применимы. В этом случае разработаны теории, описывающие образование поверхностей разрывов при приложении растягивающих усилий. Наиболее распространенные из них -теория Гриффитса.

В отличии от металлов горные породы не имеют явно выраженного предела текучести ни при одноосном растяжении, ни при сжатии. Действительные характерные кривые деформирования показаны на рис. LM, где F_c, F_t определяют прочность на сжатие и растяжение соответственно. В этом случае параметры сжатия положительны, растяжения отрицательны (в теории упругости наоборот). Это связано с тем, что в земной коре в обычных условиях горные породы подвергаются, как правило, сжатию и разрушаются чаще всего от сжатия.

Термин «хрупкое разрушение» относится к зарождению трещин, их развитию и разделению тела на две или более части, в результате чего образуются свободные поверхности, на которых полностью нарушены нормальные связи. Такое разрушение отличается от вязкого разрушения при котором образуется сложное поле перемещения поперёк или вдоль поверхности разрушения в теле; при этом нормальные к поверхности разрушения связи полностью не разрушаются. Т.о. хрупкий материал разрушается в результате образования поверхности разрыва. Широкое распространение имеют теории Мизеса и Треска — Сен -Венана.

Условие Треска — Сен — Венана предполагает, что пластическое течение наступает тогда, когда касательное напряжение достигает предела текучести материала при простом растяжении ε|τ₂|=|σ₁-σ₃|=σ₂,

В соответствии с условием Мизеса пластическое состояние наступает тогда, когда удельная энергия изменения формы достигает определенной величины. Удельная упругая энергия деформирования

Представим U как сумму удельных энергий упругого изменения объема Uo и упругого изменения формы Uф :

Тогда удельное изменение удельной формы

Поясним обозначение σi. На направлениях главных напряжений как на осях координат, построим элементарный октаэдр. Нормальные напряжения, действующие на гранях октаэдра

Величина, пропорциональная , а именно называется

интенсивностью касательного напряжения .

Из выражения (1.18) следует, что момент достижения предельного состояния при переходе от упругого к пластическому однозначно определяется интенсивностью касательных напряжений.

Условие Мизеса учитывает все три главных напряжения и в случае трехосного напряженного состояния оно точнее, чем условие Треска — Сен -Венана.

Источник

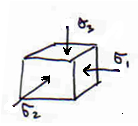
Обзор различных типов напряженных состояний. Привести примеры.

К первому классу относят трехосные растяжения, т.е. такие напряженные состояния, в которых не одно из главных напряжений не является сжимающим.

В частном случае все три главных растягивающих напряжения могут быть равными; такое напряженное состояния называется чистым

Встречается напряженное состояние, в котором

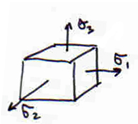
,т.е. двухосное растяжение, также относящееся к рассматриваемому классу. Также есть равное, если . К первому классу также относится одноосное напряжение, возникающее в одноосном стержне при его растяжении или чистом изгибе

Второй распространенный класс составляют такие напряженные состояния, в которых ни одно из главных напряжений не является растягивающим. Это – трехосные сжатия.

К третьему классу относятся так называемые смешанные напряженные состояния, в которых наибольшее и наименьшее из главных напряжений имеют разные знаки. Напряжение может быть как положительным, так и отрицательным.

Билет 19

1. Теория начала текучести наибольших касательных напряжений. Вывод.

Мы принимаем, что шаровой тензор не создаёт пластических деформаций; следовательно за них отвечает девиатор.

Считается, что пластические деформации возникают, когда наибольшие касательные напряжения достигают величины, характерной для материала.

Гипотеза Кулона, Треска, Сен-Венана:

Два напряженных состояния называются равноопасными, если у них равны максимальные касательные напряжения.

2. Влияние концентрации напряжений на усталостную прочность. Билет 20

Напряженное состояние в тонкостенной трубке с днищами, нагруженной наружным (внешним) давлением. Получить формулы для определения .

2. Определение перемещений в статически неопределимых стержневых системах

Перемещение ищем после того, как раскрыта статическая неопределённость и построена суммарная эпюра моментов.

Чтобы ещё раз не раскрывать статическую неопределённость, перемещение будем искать не для заданной системы, а для эквивалентной.

Для этого берём любую эквивалентную систему, разгружаем область внешних сил и, согласно интегралам Мора, прикладываем единичный фактор в направлении искомого перемещения.

После перемножаем суммарную эпюру М с эпюрой единичного фактора, используя графоаналитический способ взятия интегралов Мора.

Рассмотрим 2 эквивалентные системы:

Как видно, получили одинаковые результаты, т.е. от выбора эквивалентной системы ничего не зависит.

1. . Теория напряжений. Главные напряжения и определение их в общем случае напряженного состояния. Вывод.

2. Устойчивость продольно сжатых стержней. Коэф-т приведения длины стойки (примеры).

Устойчивость – св-во системы сохранять своё состояние при внешних воздействиях.

Пусть стержню сообщили отклонение от положения равновесия. Если после устранения причин, вызвавших отклонение, система возвращается в исходное состояние равновесия, то последнее считается устойчивым, если нет, то положение считается неустойчивым.

Критическая сила – сила, превышение которой приводит к переходу от устойчивого равновесия к неустойчивому. Общее выражение для сжатого стержня:

где — коэф-т приведения длины, — число полуволн в изогнутой оси сжатого стержня.

показывает, во сколько раз следует увеличить длину шарнирно опёртого стержня, чтобы для него равнялась для стержня длиной в рассматриваемых условиях закрепления.

Источник