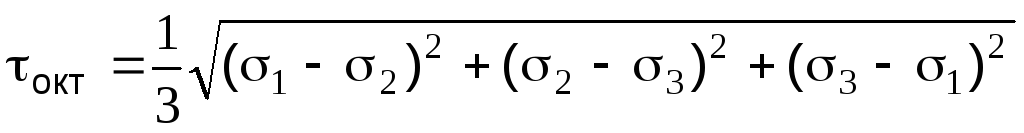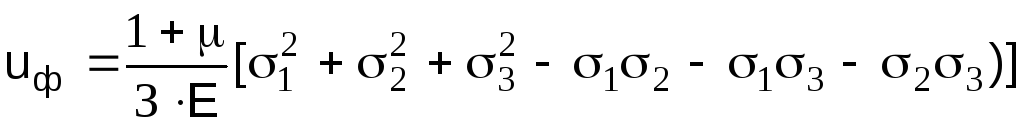Тензор напряжений круг мора

11.10. Круги напряжений Мора

Удобное двумерное геометрическое представление трёхмерного напряжённого состояния было предложено немецким учёным О. Мором. Отнесём материальную частицу к главным осям (рис. 11.21). Рассечём её плоскостью, содержащей направление третьей главной оси (рис. 11.21,а). Тогда, согласно (11.35), имеем:

Уравнения (11.59) представляют собой параметрические уравнения окружности, каноническое уравнение которой имеет в системе координат вид (рис. 11.22):

Координаты центра окружности , радиус .

Окружность Мора позволяет графически найти напряжение на любой площадке, положение которой характеризуется углом Для этого нужно отложить по часовой стрелке угол и провести под этим углом радиус R до пересечения с окружностью в точке М. Координаты этой точки и есть искомое значения . Наибольшее касательное напряжение возникает при и равно численно радиусу окружности Мора:

Минимальное значение возникает на площадке при и равно:

Аналогичные круги Мора можно построить для наклонных площадок, содержащих главные направления 1 и 2 (рис. 11.23).

Их уравнения в параметрической форме имеют вид:

откуда следует, что наибольшее касательные напряжения в этих случаях:

также равны радиусам соответствующих кругов Мора.

носят название главных касательных напряжений. Они удовлетворяют тождеству

Каждой точке на любой из окружности Мора отвечают напряжения и площадки, направление которой характеризуется одним из углов Те площадки, которые не содержат ни одну из главных осей, окружностями Мора не описываются. Можно показать, что напряжения на этих площадках задаются точками, расположенными между окружностями в заштрихованной области. Из рис. 11.24 видно, что:

Следовательно, определяется радиусом большого круга Мора. Величину

называют параметром вида напряжённого состояния Лоде. При наложе-

нии на напряжённое состояние частицы всестороннего давления параметр Лоде не изменяется. Для одноосного растяжения имеем , для сжатия имеем , для плоского чистого сдвига . Соответствующие круги Мора приведены на рис. 11.25.

Таким образом, параметр Лоде характеризует вид напряжённого состояния.

Если изначально напряжённое состояние не является двухосным, связанным с главными осями, то для построения круга напряжений Мора при плоском напряжённом состоянии следует использовать формулы (11.35):

Поступая так же, как и в случае двухосного растяжения сводим пара-

метрические уравнения окружности (11.63) к каноническому виду

В (11.64) мы имеем более сложное выражение радиуса окружности:

При уравнение (11.64) сводится к (11.60) как частному случаю.

При построение круга Мора показано на рис. 11.26. Сначала определяется положение центра С круга как точки с координатами

Затем определяется положение точки А, характеризующей напряжения на грани х элемента при , т.е. . Здесь следует пом-

нить правило знаков для и других напряжений, указанных на

рис. 11.12. Заметим, что точки А и В, характеризующие напряжения на площадках, расположенных под углом 90 0 друг к другу, лежат на противо-

положных концах диаметра круга Мора. Далее на АВ с центром в точке С чертится круг. Напряжения на произвольной площадке, лежащей под углом к оси х, можно определить следующим образом. Отклады-

ваем от точки А по часовой стрелке угол и определяем положение точки М на круге с искомыми координатами . Точка М / , диаметра-

льно противоположная Д, даёт напряжения для площадки, состав-

ляющей угол 90 0 с той, которая имеет нормаль , т.е. для площадки с уг-

лом с осью х. Точка Д даёт максимальное касательное напряже-

ние, равное радиусу круга Мора:

Одной из важных задач использования круга Мора является определе-

ние главных нормальных напряжений и . Этим напряжениям отве-

чают точки Р₁ и Р₂ круга. Из рис. 11.26 следует, что угол между направле-

ниями на точки А и Р₁ равен удвоенному углу , определяющему первое главное напряжение, а угол между направлениями А и Р₂ – удвоенный угол , определяющий второе главное направление. Имеет место соотношение

которое совпадает с формулой (11.36).

Из изложенного следует, что круг Мора можно использовать в качес-

тве графического способа определения как напряжений на произвольной площадке, так и главных нормальных и максимальных касательных напря-

Читайте также: Цвет моря код цвета

Источник

Круги Мора. Обобщенный Закон Гука. / Сопромат

Круги Мора-круговые диаграммы, дающие наглядное представление о напряжениях в разных сечениях, проходящих через данную точку. Координаты точек круга соответствуют нормальным и касательным напряжениям на различных площадках. Откладываем от оси  из центра С луч под углом 2 (>0, то против час.стр.), находим точку D,

координаты которой: _,_. Можно графически решать как прямую, так и обратную задачи.

Объемное напряженное состояние

Напряжения в любой площадке при известных главных напряжениях ₁, ₂, ₃:

;

где ₁, ₂, ₃ — углы между нормалью к рассматриваемой площадке и направлениями главных напряжений.

Наибольшее касательное напряжение: .

Оно действует по площадке параллельной главному напряжению ₂ и наклоненной под углом 45 о к главным напряжениям ₁ и ₃.

Круг Мора для объемного напряженного состояния.

Точки, являющиеся вершинами кругов соответствуют диагональным площадкам, наклоненным под 45 о к главным напряжениям:

, (иногда называют главными касательными напряжениями).

Плоское напряженное состояние — частный случай объемного и тоже может быть представлено тремя кругами Мора, при этом одно из главных напряжений должно быть равно 0. Для касательных напряжений также, как и при плоском напряженном состоянии, действует закон парности: составляющие касательных напряжений по взаимно перпендикулярным площадкам, перпендикулярные к линии пересечения этих площадок, равны по величине и обратны по направлению.

Напряжения по октаэдрической площадке.

Октаэдрическая площадка (АВС) – площадка, равнонаклоненная ко всем главным направлениям.

;

Октаэдрическое нормальное напряжение равно среднему из трех главных напряжений.

или , Октаэдрическое касательное напряжение пропорционально геометрической сумме главных касательных напряжений. Интенсивность напряжений:

_x+_y+_z=₁+₂+₃ — сумма нормальных напряжений, действующих по любым трем взаимно перпендикулярным площадкам есть постоянная величина, равная сумме главных напряжений (первый инвариант).

Деформации при объемном напряженном состоянии.

Обобщенный закон Гука (закон Гука при объемном напряжении):

₁,₂,₃ — относительные удлинения в главных направлениях (главные удлинения). Если какие-либо из напряжений _i будут сжимающими, то их необходимо подставлять в формулы со знаком минус.

Относительная объемная деформация:

Изменение объема не зависит от соотношения между главными напряжениями, а зависит от суммы главных напряжений. Т.е. элементарный кубик получит такое же изменение объема, если к его граням будут приложены одинаковые средние напряжения: , тогда , где К= — модуль объемной деформации. При деформации тела, материал которого имеет коэффициент Пуассона = 0,5 (например, резина) объем тела не меняется.

Потенциальная энергия деформации

При простом растяжении (сжатии) потенциальная энергия U=.

Удельная потенциальная энергия — количество потенциальной энергии, накапливаемое в единице объема: u = ; . В общем случае объемного напряженного состояния, когда действуют три главных напряжения:

или

Полная энергия деформации, накапливаемая в единице объема, может рассматриваться как состоящая из двух частей: 1) энергии u_o, накапливаемой за счет изменения объема (т.е. одинакового изменения всех размеров кубика без изменения кубической формы) и 2) энергии u_ф, связанной с изменением формы кубика (т.е. энергии, расходуемой на превращение кубика в параллелепипед). u = u_о + u_ф.

;

— тензор напряжений (матрица третьего порядка).

При переходе к главным напряжениям тензор напряжений получает вид:

. При повороте системы координат коэффициенты тензора меняются, сам тензор остается постоянным. Три инварианта напряженного состояния:

Аналогичные зависимости возникают при рассмотрении деформированного состояния в точке. Сопоставление зависимостей напряженного и деформированного плоского состояния (аналогия):