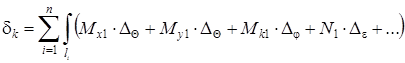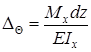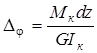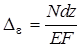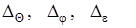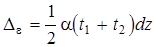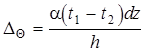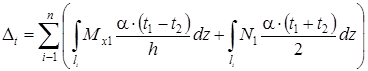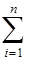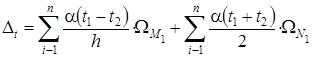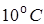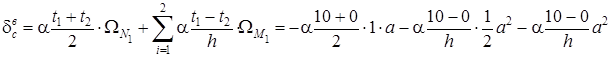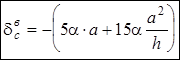Лекции и задачи по строительной механике
Определение перемещений от действия температуры
Интеграл Мора, как отмечалось в предыдущем подразделе, может быть представлен в следующем виде:
. (5.33)
В выражении (5.33) взаимный угол поворота торцевых сечений (рис. 5.19) элемента, имеющего бесконечно малую длину ds стержня от заданной внешней нагрузки; взаимное смещение торцевых сечений ds; взаимное смещение торцевых сечений вдоль оси, перпендикулярной оси элемента. В таком виде интеграл Мора может быть использован для определения перемещений не только от действия сил, но и от температуры.
Пусть верхнее волокно элемента ds нагрето на t1, а нижнее на t2. При этом t1 t2 . Распределение температуры по высоте сечения принято по прямолинейному закону. При температурном коэффициенте линейного расширения верхнее волокно удлинится на t1ds , а нижнее на t2ds. На уровне нейтральной оси это удлинение, что очевидно из рис. 5.19, составит полусумму удлинений верхнего и нижнего волокон элемента ds.
. (5.34)
Выражение (5.34) соответствует тому состоянию элемента ds, при котором он по всей высоте сечения h получил равномерное изменение температуры. От неравномерного нагрева торцевые сечения элемента ds поворачиваются на угол
. (5.35)
Деформация сдвига в элементе ds не возникает, т.е.
Подставляя (5.34) и (5.35) в (5.33), получим интеграл Мора для определения температурных перемещений.
. (5.36)
Интеграл Мора (5.34) значительно упрощается тогда, когда интегрирование ведётся для прямолинейных или ломаных стержней, имеющих по длине постоянное поперечное сечение. В этом случае интегралы могут быть определены, как площади единичных эпюр.
, (5.37)
где и — площади единичных эпюр и .
При поперечном сечении элемента, несимметричном относительно нейтральной оси, в формулах (5.34) и (5.35) во втором слагаемом множитель, связанный с температурой, принимает вид , где у расстояние от нижнего волокна до горизонтальной оси, проходящей через центр тяжести. При этом необходимо помнить следующее правило знаков: если деформации элемента ds от температуры и от единичной силы одного знака, то соответствующие слагаемые в формулах (5.34) и (5.35) будут положительными, и соответственно наоборот.
Определение перемещений от осадки опор
При перемещениях опор любой статически определимой конструкции в её опорных закреплениях опорные реакции не возникают.
Пусть опора В рамы, представленной на рис. 5.20, получила осадку на величину . При определении линейного перемещения произвольной точки, например к, в единичном состоянии к этой точке в направлении искомого перемещения прикладывают сосредоточенную силу . От действия этой силы определяют опорные реакции.
На основании принципа возможных перемещений можно составить следующую аналитическую зависимость:
(5.38)
Действительное состояние Единичное состояние
В соответствии с третьим уравнением в (5.37) можно записать общую формулу для определения перемещений от i-й осадки опор:
. (5.39)
Произведение в (5.37) считается положительным, если опорная реакция направлена в противоположную сторону от осадки опор.
Источник
Расчет перемещений от изменения температуры
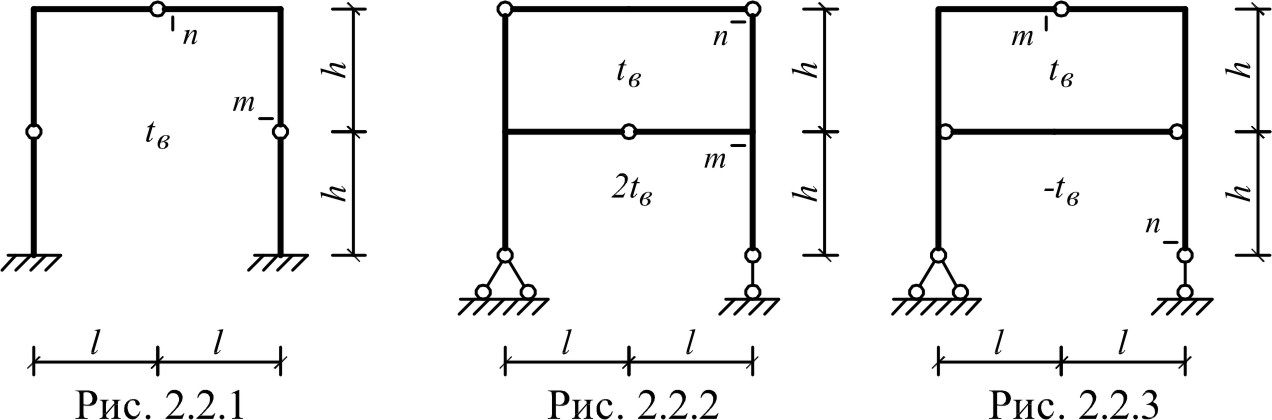
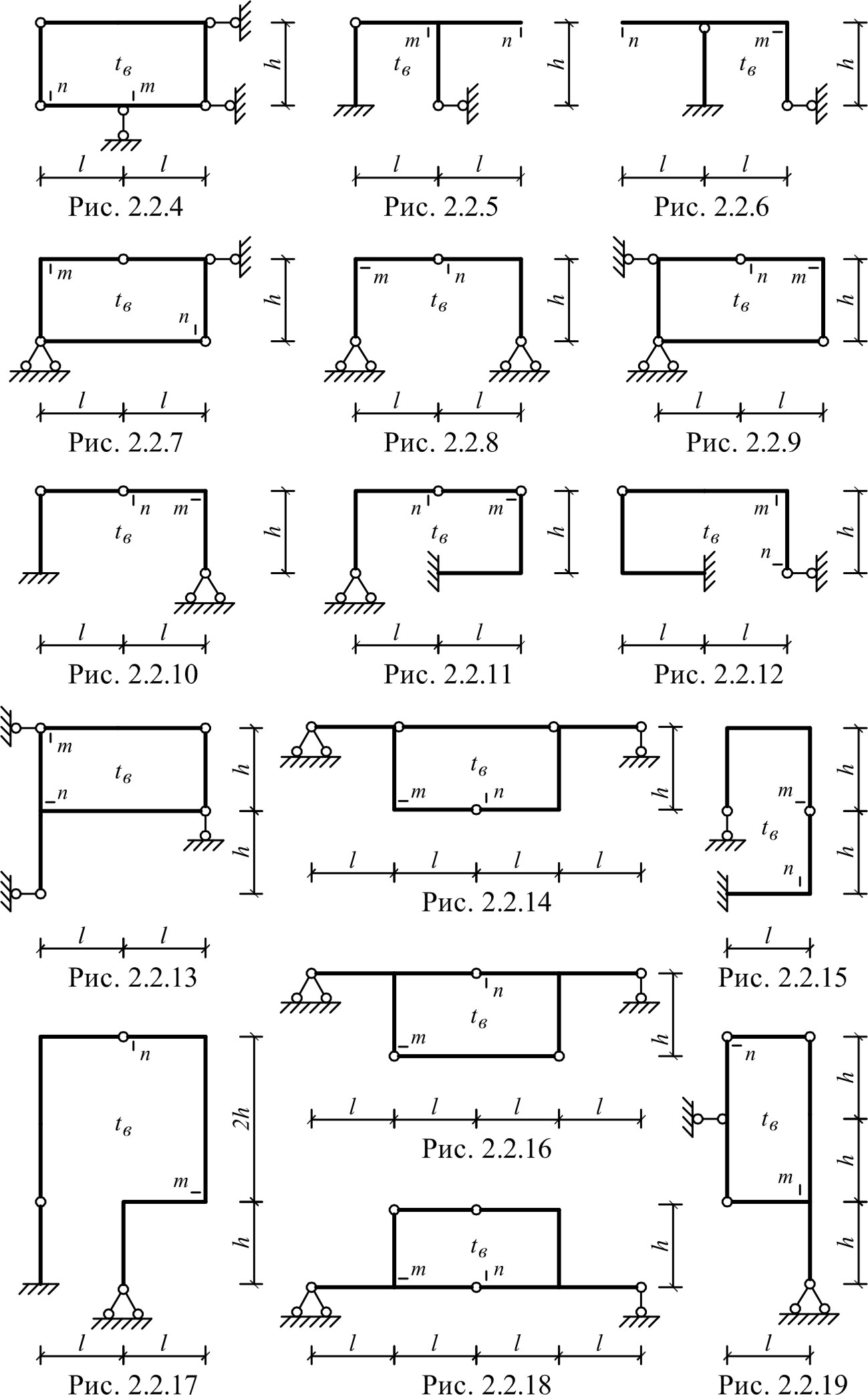
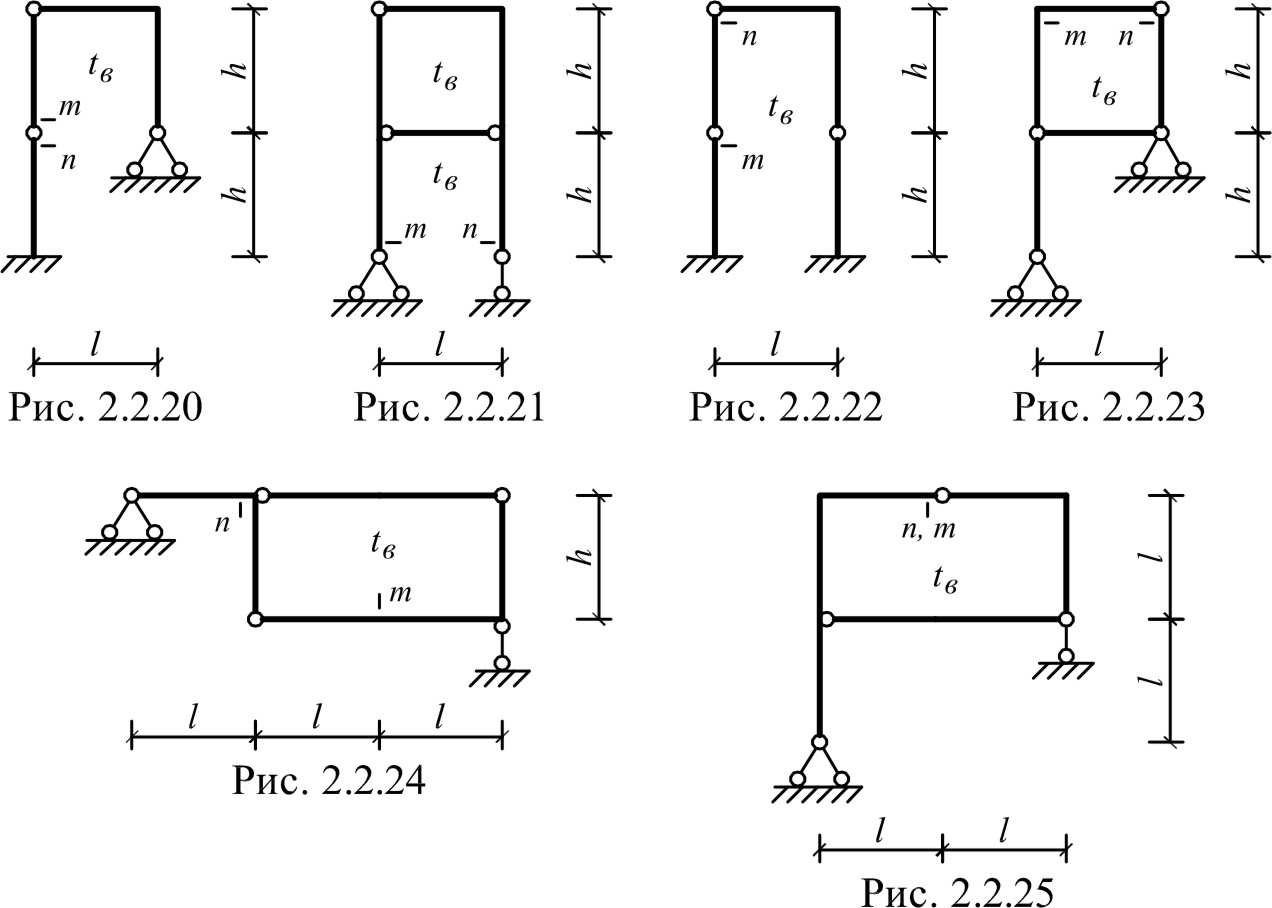
Для одной из рам, изображенных на рис. 2.2.1 – 2.2.25, требуется определить линейное перемещение сечения m и угол поворота сечения n. При расчете перемещений принять:
- высоту поперечного сечения всех стержней hc=0,1l;
- положение центра тяжести поперечного сечения посередине его высоты;
- коэффициент линейного расширения одинаковым для всех элементов системы и равным = 10 -5 1/град;
- параметр температуры t = 10 C (на схемах рам температура снаружи tн не показана).
Исходные данные принять из табл. 2.2.
Температуры снаружи, tн
Пример решения задачи
Исходные данные: схема рамы на рис. 2.2.25; l=2 м; h=2 м; tн= t; tв= -4t; l=2 м; t=10 C.
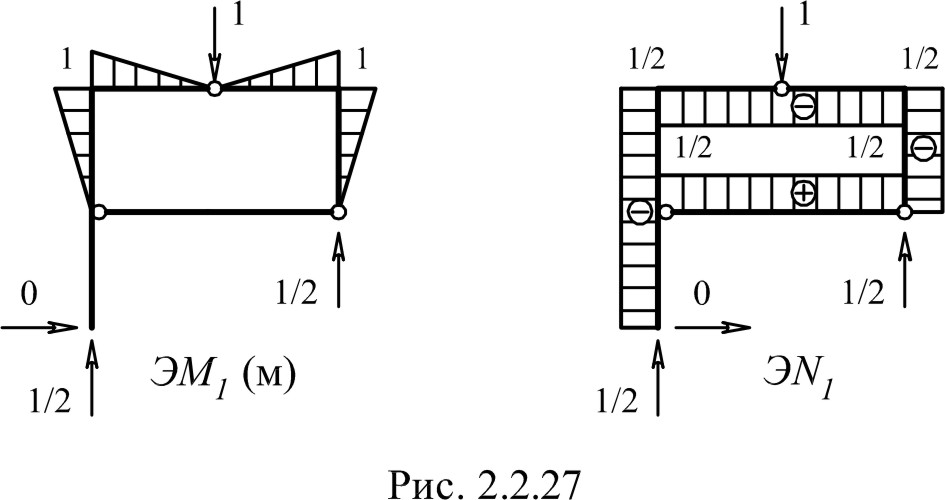
- Эпюры изгибающих моментов и продольной силы в раме от единичной силы, приложенной в сечении m (для определения вертикального перемещения сечения m)
- Эпюры изгибающих моментов и продольной силы в раме от единичного момента, приложенного в сечении n (для определения угла поворота сечения n)
- В формуле Мора первый член учитывает влияние температурного удлинения (укорочения) стержней рамы на величину отыскиваемого перемещения, а второй член – влияние на перемещение температурного искривления стержней.
- Знак первого члена формулы Мора устанавливается в зависимости от знака температуры на оси стержня (t’) и знака эпюры продольной силы; знак второго члена зависит от направления температурной кривизны и кривизны от изгиба, вызванного единичной силой. Если на каком-либо участке эти кривизны совпадают, то знак второго члена принимается положительным, в противном случае – отрицательным.
– коэффициент линейного расширения;
t’=( tн + tв)/2 – температура на оси стержня;
t’’=| tн — tв |;
ωN1, ωM1 – площадь эпюры соответственно N1 и M1 на участке (стержне).
Пояснения к решению задачи
Учебники (учебные пособия)
Н.Н. Анохин. Строительная механика в примерах и задачах. Часть I. Статически определимые системы.
А.Ф. Смирнов и др. Строительная механика (стержневые системы).
Снитко Н.К. Строительная механика
А.В. Дарков, Н.Н. Шапошников. Строительная механика.
Руководство к практическим занятиям по курсу строительной механики (под ред. Г.К. Клейна)
А.П. Мельчаков, А.С. Сытник. Построение эпюр внутренних силовых факторов в плоских рамах. Учебное пособие.
Источник
Расчет перемещений от изменения температуры
Для одной из рам, изображенных на рис. 2.2.1 – 2.2.25, требуется определить линейное перемещение сечения m и угол поворота сечения n. При расчете перемещений принять:
— высоту поперечного сечения всех стержней hc= 0,1 l;
— положение центра тяжести поперечного сечения посередине его высоты;
— коэффициент линейного расширения одинаковым для всех элементов системы и равным a = 10 -5 1/град;
— параметр температуры t = 10 °C (на схемах рам температура снаружи tн не показана).
Исходные данные принять из табл. 2.2.
| Номер варианта | |||||||
| Температуры снаружи, tн | t | -t | 2t | -2t | 4t | 3t | -3t |
| Температура внутри, tв | -2t | -3t | 4t | 4t | -4t | -t | t |
| l, м | 2,5 | ||||||
| h, м | 2,5 |
Пример решения задачи
Исходные данные: схема рамы на рис. 2.2.25; l= 2 м; h= 2 м; tн= t; tв= -4t; l= 2 м; t= 10 °C.
а) Эпюры изгибающих моментов и продольной силы в раме от единичной силы, приложенной в сечении m (для определения вертикального перемещения сечения m)
б) Эпюры изгибающих моментов и продольной силы в раме от единичного момента, приложенного в сечении n (для определения угла поворота сечения n)
в) Линейное (Δ m) перемещение сечения m и угловое (φ n) перемещение сечения n, найденные по формуле Мора
| , | |
| где | a – коэффициент линейного расширения; |
| t’=(tн + tв)/2 – температура на оси стержня; | |
| t’’=| tн — tв |; | |
| ωN1, ωM1 – площадь эпюры соответственно N1 и M1 на участке (стержне). |
| (м) = м = 6,45 мм, |
| (рад) = 0,004425 рад. |
Пояснения к решению задачи
1) В формуле Мора первый член учитывает влияние температурного удлинения (укорочения) стержней рамы на величину отыскиваемого перемещения, а второй член – влияние на перемещение температурного искривления стержней.
2) Знак первого члена формулы Мора устанавливается в зависимости от знака температуры на оси стержня (t’) и знака эпюры продольной силы; знак второго члена зависит от направления температурной кривизны и кривизны от изгиба, вызванного единичной силой. Если на каком-либо участке эти кривизны совпадают, то знак второго члена принимается положительным, в противном случае – отрицательным.
Учебники (учебные пособия)
| Шифр библиотеки ЮУрГУ | Автор(ы), название учебника (учебного пособия) |
| 624.04(07) А697 | Н.Н. Анохин. Строительная механика в примерах и задачах. Часть I. Статически определимые системы. |
| 624.04(07) С863 | А.Ф. Смирнов и др. Строительная механика (стержневые системы). |
| 624.04(07) С535 | Снитко Н.К. Строительная механика |
| 624.04(07) Д203 | А.В. Дарков, Н.Н. Шапошников. Строительная механика. |
| 624.04(07) Р851 | Руководство к практическим занятиям по курсу строительной механики (под ред. Г.К. Клейна) |
| 624.07(07) М487 | А.П. Мельчаков, А.С. Сытник. Построение эпюр внутренних силовых факторов в плоских рамах. Учебное пособие. |
Расчет перемещений от кинематического воздействия
Формулировка задачи
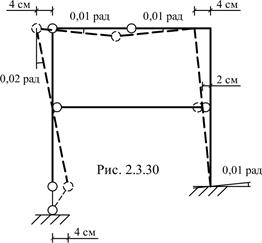
Для одной из рам, изображенных на рис. 2.3.1 – 2.3.25 требуется:
— определить линейное и угловое перемещение сечения n и взаимный угол поворота сечений m и k;
— изобразить изменение геометрии рамы от кинематического воздействия
При расчете перемещений принять: D = 10 -2 l, j = D/l.
Исходные данные принять из табл. 2.3.
| Номер варианта | |||||||
| l, м | 1,5 | 2,0 | 2,5 | 3,0 | 3,25 | 2,75 | 1,75 |
| h, м | 2,5 |
а) Единичное состояние и реакции в связях для определения линейного перемещения сечения n
б) Единичное состояние и реакции в связях для определения углового перемещения сечения n
в) Единичное состояние и реакции в связях для определения взаимного угла поворота сечений m и k
г) Линейное и угловые перемещения сечений от заданного смещения и неточности изготовления связей, найденные по формуле Мора
| , | |
| где | Rj1 – реакция в j -той связи в соответствующем единичном состоянии; |
| Sj – заданное перемещение (неточность изготовления) j -той связи. |
д) Геометрия рамы с учетом заданных смещений связей
Пояснения к решению задачи
1) Знак произведения Rj1∙Sj устанавливается по правилу: если направление реакции совпадает с направлением заданного перемещения связи, то знак произведения положительный; в противном случае – отрицательный.
2) При заданной неточности изготовления элемента вышеприведенное правило знаков сохраняется, но в этом случае роль реакции играет внутренний силовой фактор в сечении элемента по направлению заданной неточности.
Учебники (учебные пособия)
| Шифр библиотеки ЮУрГУ | Автор(ы), название учебника (учебного пособия) |
| 624.04(07) А697 | Н.Н. Анохин. Строительная механика в примерах и задачах. Часть I. Статически определимые системы. |
| 624.04(07) С863 | А.Ф. Смирнов и др. Строительная механика (стержневые системы). |
| 624.04(07) С535 | Снитко Н.К. Строительная механика |
| 624.04(07) Д203 | А.В. Дарков, Н.Н. Шапошников. Строительная механика. |
| 624.04(07) Р851 | Руководство к практическим занятиям по курсу строительной механики (под ред. Г.К. Клейна) |
| 624.07(07) М487 | А.П. Мельчаков, А.С. Сытник. Построение эпюр внутренних силовых факторов в плоских рамах. Учебное пособие. |
Источник
Перемещения от действия температуры
, (3)
где: — взаимный угол поворота торцевых сечений элемента длиной dz при изгибе от заданной нагрузки;
— взаимный угол закручивания торцевых сечений элемента длиной dz от заданного крутящего момента;
— взаимное смещение торцевых сечений элемента длиной dz от действия заданной осевой силы.
В таком виде формула Мора может быть использована не только когда деформации элемента dz вызваны силовым воздействием на систему, но и в случае, если они вызваны действием температуры. Значит, формула Мора в виде () может быть использована для определения перемещений системы, вызванных действием температуры.
Рассмотрим элемент стержня длиной dz, у которого верхние волокна нагреты на 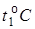
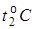
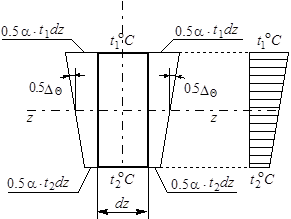
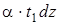
– удлинение нижнего волокна элемента
– удлинение на оси z:
– угол взаимного поворота торцевых сечений элемента dz:
Деформаций кручения 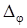
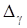
Подставив полученные выражения в (3), получим формулу для отыскания температурных перемещений:
(4)
Знак означает суммирование по всем стержням и участкам упругой системы. Если по длине стержня величины t 1, t 2, и h не меняются, то формула (4) принимает вид
(5)
Здесь 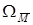
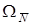
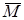
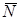
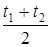
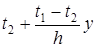
Знаки членов формулы (5) определяются так: если деформации элемента dz от температуры и от единичной силы аналогичны друг другу, то знак соответствующего члена будет положительным, и наоборот.
При определении перемещений от действия температуры нельзя пренебрегать членом формулы (5), зависящим от продольной силы.
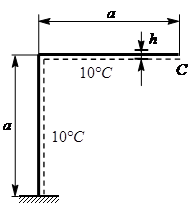 |
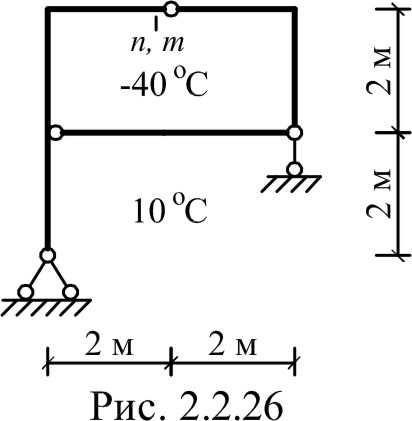
Г – образная рама нагревается изнутри на . Снаружи температура не изменяется. Сечение постоянное, высота его равна h. Величина a — известна.
найти вертикальное перемещение .
Изображаем раму в двух состояниях:
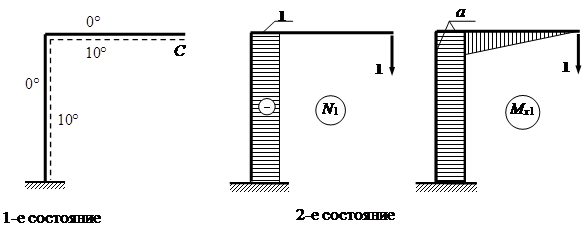 |
Подсчитаем перемещение по формуле (5):
.
Знак “минус” означает, что перемещение происходит в направлении, противоположном направлению единичной нагрузки.
Источник