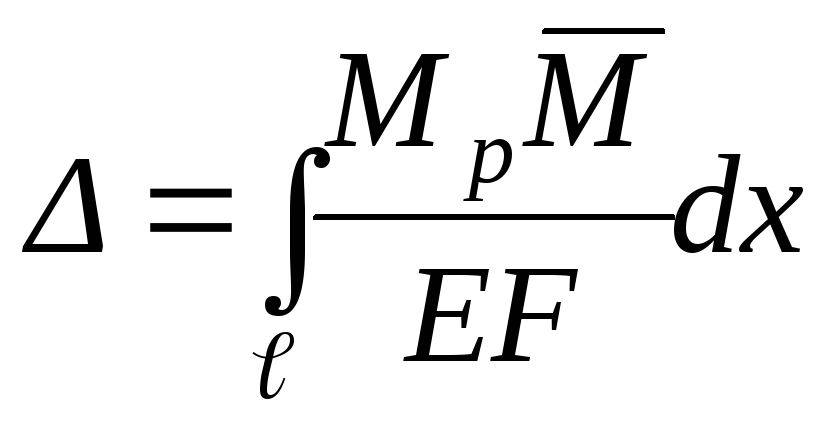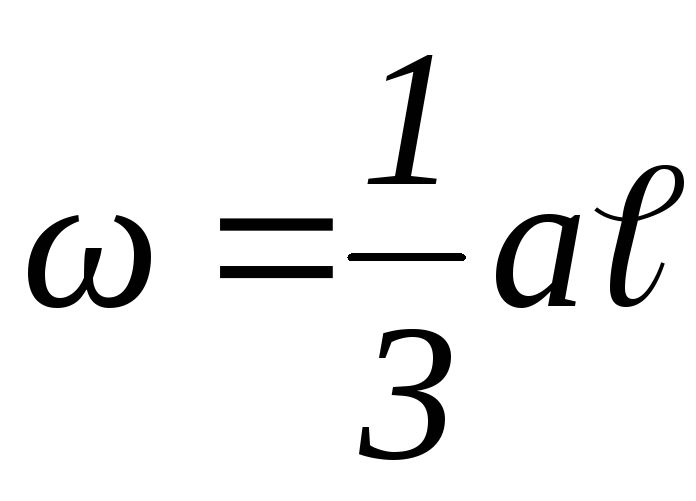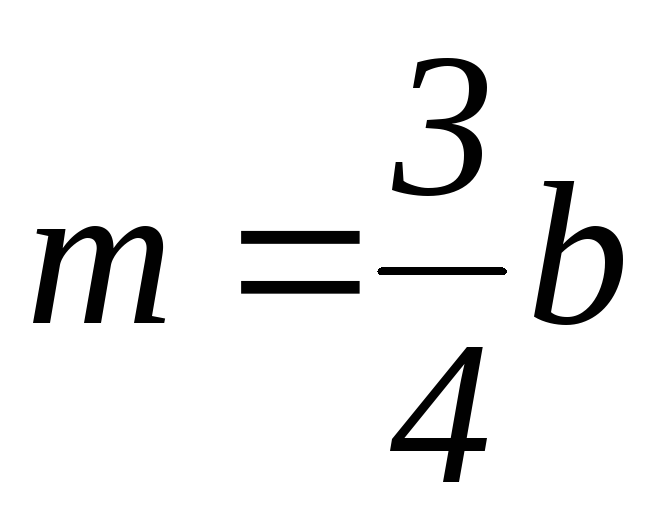- Перемножение эпюр по правилу, методу или способу Верещагина
- Верещагин и его метод, правило или способ
- Площадь и центр тяжести эпюр
- Перемножение простейших эпюр по Верещагину
- Прямоугольник на прямоугольник
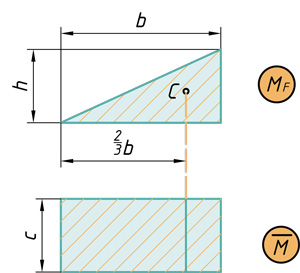
- Прямоугольник на треугольник
- Треугольник на прямоугольник
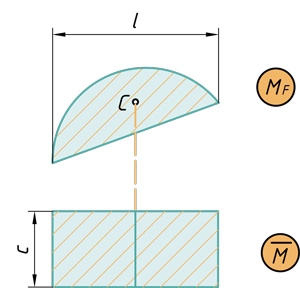
- Параболический сегмент на прямоугольник
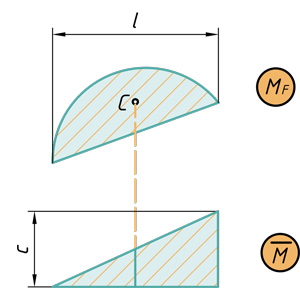
- Параболический сегмент на треугольник
- Расслоение эпюр на простые фигуры
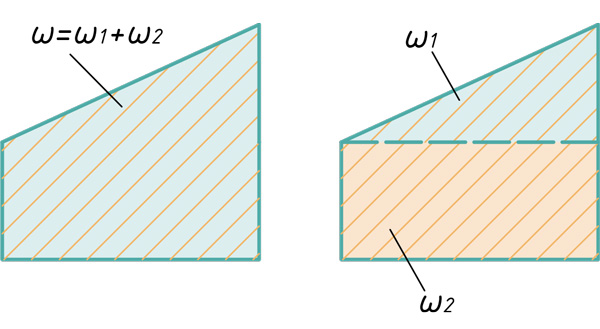
- Прямоугольник и треугольник
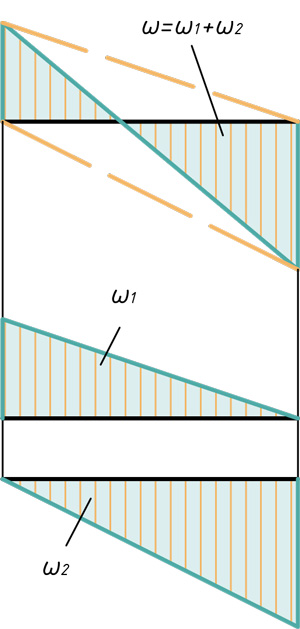
- Два треугольника
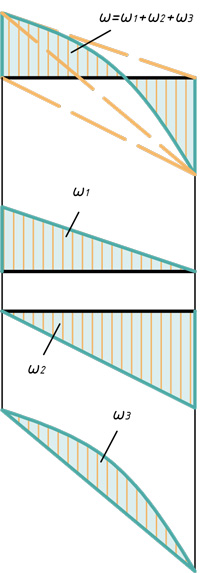
- Два треугольника и параболический сегмент
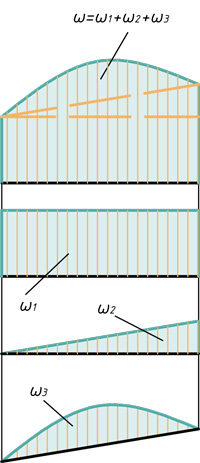
- Треугольник, прямоугольник и параболический сегмент
- Пример определения перемещений: прогибов и углов поворотов по Верещагину
- Построение эпюры изгибающих моментов
- Построение единичных эпюр
- Перемножение участков эпюры по Верещагину
- Определение прогиба сечения С
- Определение угла поворота сечения С
- 1.6. Графический способ вычисления интеграла Мора – способ Верещагина
- Глава 2. Статически неопределимые балки
- 2.1. Общие понятия
- Вычисление интеграла Мора способом Верещагина
Перемножение эпюр по правилу, методу или способу Верещагина
Привет! В этой статье будем учиться определять перемещения поперечных сечений при изгибе: прогибы и углы поворотов, по методу (способу, правилу) Верещагина. Причем это правило широко используется не только при определении перемещений, но и при раскрытии статической неопределимости систем по методу сил. Я расскажу, о сути этого метода, как перемножаются эпюры различной сложности и когда выгодно пользоваться этим методом.
Что нужно знать для успешного освоения материалов данного урока? Обязательно нужно уметь строить эпюры изгибающих моментов, т.к. в этой статье будем работать с данной эпюрой.
Верещагин и его метод, правило или способ
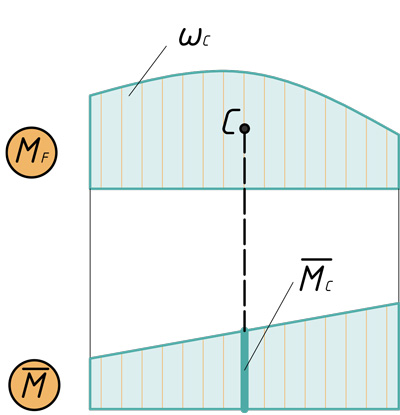
А.К. Верещагин в 1925г. предложил более простой способ решения (формулы) интеграла Мора. Он предложил вместо интегрирования двух функций перемножать эпюры: умножать площадь одной эпюры на ординату второй эпюры под центром тяжести первой. Этим способом можно пользоваться, когда одна из эпюр прямолинейна, вторая может быть как линейной, так и параболической. Кроме того, ордината берется прямолинейной эпюры. Когда эпюры обе прямолинейны, то тут совсем неважно, чью брать площадь, а чью ординату. Таким образом, эпюры по Верещагину перемножаются по следующей формуле:
Проиллюстрировано перемножение эпюр по Верещагину: C — центр тяжести первой эпюры, ωс — площадь первой эпюры, Mc — ордината второй эпюры под центром тяжести первой.
Площадь и центр тяжести эпюр
При использовании метода Верещагина берется не сразу вся площадь эпюры, а частями, в пределах участков. Эпюра изгибающих моментов расслаивается на простейшие фигуры.
Любой самый сложный участок эпюры можно расслоить на три простейшие фигуры: прямоугольник, прямоугольный треугольник и параболический сегмент.
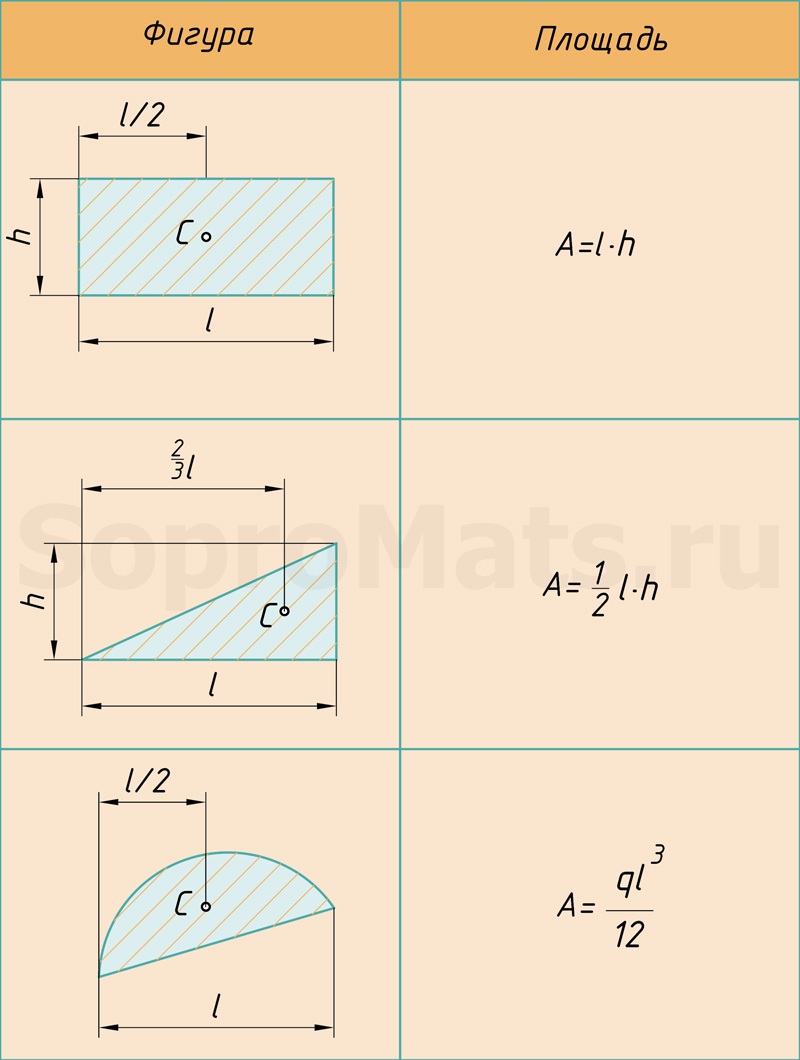
Поэтому именно с этими фигурами будем дальше работать. Напомню, как вычислить их площадь и где у них находится центр тяжести. Все формулы и размеры оформил в виде таблицы:
Перемножение простейших эпюр по Верещагину
В этом блоке статьи покажу простейшие случаи перемножения эпюр по Верещагину.
Прямоугольник на прямоугольник
Прямоугольник на треугольник
Треугольник на прямоугольник
Параболический сегмент на прямоугольник
Параболический сегмент на треугольник
Расслоение эпюр на простые фигуры
В этом блоке статьи покажу способы расслоения эпюр на простые фигуры, для дальнейшего их перемножения по правилу Верещагина.
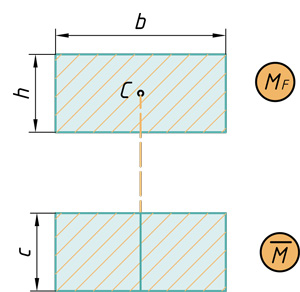
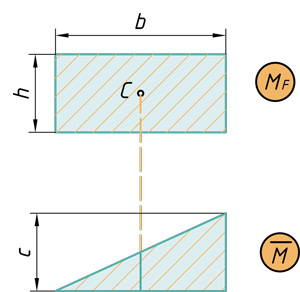
Прямоугольник и треугольник
Два треугольника
Два треугольника и параболический сегмент
Треугольник, прямоугольник и параболический сегмент
Пример определения перемещений: прогибов и углов поворотов по Верещагину
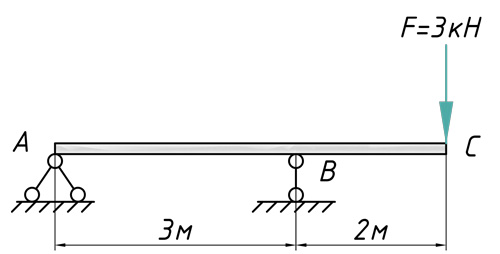
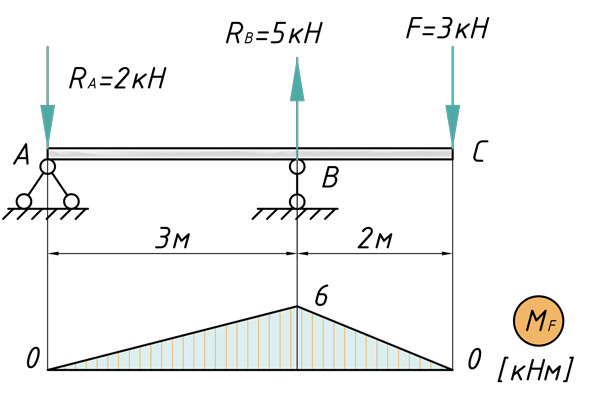
Теперь предлагаю рассмотреть конкретный пример с расчетом перемещений поперечных сечений: их прогибов и углов поворотов. Возьмем стальную балку, которая загружена всевозможными типами нагрузок и определим прогиб сечения C, а также угол поворота сечения A.
Построение эпюры изгибающих моментов
В первую очередь рассчитываем и строим эпюру изгибающих моментов:
Построение единичных эпюр
Теперь для каждого искомого перемещения необходимо приложить единичную нагрузку в ту точку, где это перемещение определяется и построить единичные эпюры:
- для прогибов прикладываются единичные силы.
- для углов поворотов прикладываются единичные моменты.
Все прикладываемые нагрузки являются безразмерными величинами. Причем, направление этих нагрузок неважно! Расчет покажет верное направление перемещений.
Например, после расчета величина прогиба получилась положительной, это значит, что направление перемещения сечения совпадает с направлением ранее прикладываемой единичной силы. То же самое касается и углов поворотов.
Перемножение участков эпюры по Верещагину
После проведения всех подготовительных работ: построения эпюры изгибающих моментов, расслоения ее на элементарные фигуры и построения единичных эпюр от нагрузок, приложенных в местах и направлении искомых перемещений, можно переходить непосредственно к перемножению соответствующих эпюр.
Как уже было написано выше, линейные эпюры можно перемножать в любом порядке, то есть брать площадь любой эпюры: основной или единичной, и умножать на ординату другой. Но обычно, чтобы не путаться в расчетах, площади берут основной эпюры изгибающих моментов, в этом уроке будем придерживаться этого же правила.
Определение прогиба сечения С
Перемножаем соответствующие эпюры слева направо и вычисляем прогиб сечения C по методу Мора — Верещагина:
\[ < V >_< C >=\frac < 1 >< E< I >_ < x >> (\frac < 1 > < 2 >\cdot 6\cdot 3\cdot \frac < 2 > < 3 >\cdot 2+\frac < 1 > < 2 >\cdot 6\cdot 2\cdot \frac < 2 > < 3 >\cdot 2)=\frac < 20кН< м >^ < 3 >>< E< I >_ < x >> \]
Представим, что рассчитываемая балка имеет поперечное сечение в виде двутавра №24 по ГОСТ 8239-89, тогда прогиб балки будет равен:
Определение угла поворота сечения С
Перемножаем соответствующие эпюры слева направо и вычисляем угол поворота сечения C по правилу Мора — Верещагина:
Для закрепления пройденного материала рекомендую изучить примеры, где рассмотрены различные случаи расслоения и перемножения эпюр.
Источник
1.6. Графический способ вычисления интеграла Мора – способ Верещагина
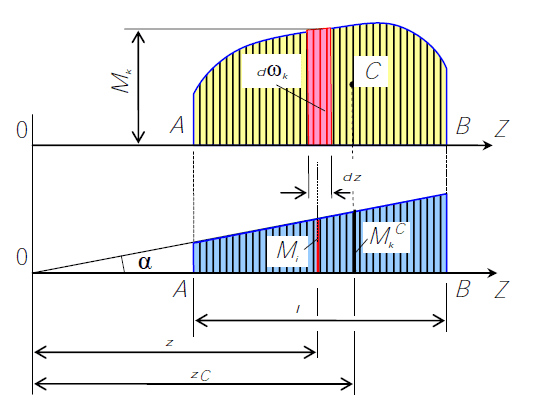
Упрощение операции интегрирования основано на том, что эпюры от единичных усилий на прямолинейных участках оказываются линейными. Рассмотрим эту процедуру применительно к участку балки. На рис.1.16 сверху показан участок балки с эпюрой Мробщего вида, а внизу эпюра, представляющая линейную функцию. Преобразуем интеграл Мора
(а)
с учётом этой особенности. Как видно из верхнего чертежа, Мрdx = dω, а из нижнего чертежа имеем. Если кроме того считать, что жёсткостьEIна протяжении участка постоянна, вместо (а) будем иметь
. (б)
Интеграл представляет собой статический момент площади эпюрыМротносительно осиу. Его можно записать иначе
Sy = ω ∙ xc ,
где ω– площадь этой эпюрыМр;
хс– координата центра тяжести эпюрыМр.
Отметив на нижней эпюре соответствующую ординату и обозначив её буквой m, будем иметь
xctg α = m.
В результате подстановки этих выражений в (б) получим
. (в)
Если балка имеет несколько участков по длине, формула Верещагина будет иметь вид
, (1.27)
где ∆ – обобщённое перемещение (либо прогиб υ, либо угол поворота θ);
ωi– площадь эпюры моментов от внешней нагрузки (грузовой эпюры);
mi– ордината единичной эпюры под центром тяжести грузовой эпюры;
n– число участков по длине балки.
При пользовании этой формулой надо уметь вычислять площади и координаты центров тяжести основных фигур: прямоугольника, прямолинейного треугольника и криволинейного треугольника. Минимально необходимые справочные данные приведены в табл.1.1. Процедуру графического вычисления называют «перемножением» эпюр.
В случае, если эпюра Мртоже линейная, операция перемножения обладает свойством коммутативности: безразлично, умножается ли площадь грузовой эпюры на ординату единичной или площадь единичной на ординату грузовой.
Встречающиеся на практике эпюры могут быть, как правило, разбиты на простые фигуры, приведённые в табл.1.1.
Эпюры Мри
Примечание: параболы – квадратные.
В качестве примера рассмотрим уже рассчитанную балку на рис.1.13. Чтобы построить эпюры Мр и , можно не определять опорные реакции: достаточно сосчитать момент на опореВ от нагрузки на консоли, построить эпюру на консоли, а затем соединить прямой линией значение М на опоре В с нулём на опоре А (рис.1.17).
В соответствии с формулой (1.27)
.
Конечно, результат получился такой же, что и при интегрировании по формуле Мора, но с меньшими затратами труда.
Глава 2. Статически неопределимые балки
2.1. Общие понятия
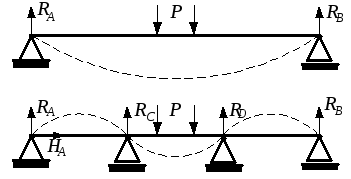
Изложенные в предыдущей главе методы определения перемещений широко применяются в расчётах статически неопределимых балок. Если при проектировании длинных балок (мостов, валов турбин) условия прочности и (или) жёсткости не выполняются, можно увеличить сечение балки, а можно поставить дополнительные опоры в пролёте (рис.2.1,б). Второй путь очень часто оказывается предпочтительным, так как позволяет, не увеличивая вес конструкции, сделать её более жёсткой.
Балка с промежуточными опорами становится статически неопределимой, так как трёх уравнений статики уже недостаточно для определения пяти неизвестных реакций.
Напомним, что простую статически неопределимую систему, образованную из стержней, работающих на растяжение-сжатие, мы рассматривали в разделе 2.5 первой части курса. Дополнительное уравнение для определения продольных сил в стержнях – уравнение совместности деформаций – было получено из рассмотрения схемы деформирования системы. Аналогичным по существу методом рассчитываются статически неопределимые балки.
Степень статической неопределимости определяется числом «лишних» связей. Балка на рис.2.1,б имеет две «лишних» промежуточных опоры – их можно удалить без ущерба для равновесия. Степень статической неопределимости этой балки равна двум.
Источник
Вычисление интеграла Мора способом Верещагина

Взятие интеграла Мора не всегда удобно и связано с необходимостью составления функции внутренних сил. Поэтому вместо интегрирования интеграла Мора можно воспользоваться графоаналитическим способом — способом перемножения эпюр (способом Верещагина). Рассмотрим этот метод подробнее.
Рассмотрим две эпюры. Пусть одна имеет произвольное очертание, а другая — прямолинейное.
Перемножение эпюры произвольного очертания и линейной эпюры способос Верещагина
Формула Верещагина:
Способ Верещагина перемножения эпюр можно сформулировать следующим образом.
Интеграл Мора равен произведению площади эпюры (любого очертания) на ординату прямолинейной эпюры, расположенную под центром тяжести эпюры Mk, деленному на жесткость стержня.
Интеграл (значение) считается положительным, если обе эпюры изгибающих моментов расположены по одну сторону от оси балки. Если перемножаемые эпюры располагаются по разные стороны от оси балки, то значение интеграла, полученное способом Верещагина, принимается отрицательным.
Отметим, что если брать интеграл непосредственно, то знак получается в результате вычислений «как бы автоматически». В способе Верещагина его следует ставить по вышеуказанному правилу.
Положительное значение интеграла означает, что направление перемещения совпадает с направлением единичной силы (или момента).
Способ вычисления интеграла Мора путем замены непосредственного интегрирования перемножением соответствующих эпюр называется способом (или правилом) Верещагина, который предложил студент МИИЖТ Верещагин в 1924.
Источник