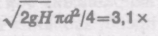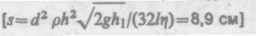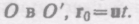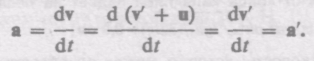Сопло фонтана дающего вертикальную струю высотой 5 м имеет форму усеченного конуса

Сопло фонтана дающего вертикальную струю высотой 5 м имеет форму усеченного конуса

2020-04-12
Сопло фонтана, дающего вертикальную струю высотой 8 м, имеет форму усеченного конуса, сужающегося вверх. Диаметр нижнего сечения 5 см, верхнего 1 см. Высота сопла 0,5 м. Определите расход воды, подаваемой фонтаном; на сколько давление в нижнем сечении больше атмосферного. Сопротивлением воздуха в струе и сопротивлением в сопле пренебрегите.

В потоке жидкости, в сопле, проведем два горизонтальных сечения: нижнее (I) и верхнее (II) сечения (рис.).

Расход воды в 1 сек равен объему жидкости $V$, протекающей за 1 сек через любое сечение S. Скорость воды, протекающей через II сечение, найдем по высоте подъема воды в поле тяжести

Применим уравнение Бернулли к потоку жидкости через I и II сечения:

Из уравнения (3) найдем избыточное давление

Для нахождения скорости воды в сечении 1 воспользуемся уравнением неразрывности струи

откуда, учтя (1), получим

Подставим уравнения (1) и (5) в уравнение (4)

$\Delta p = \rho gh + \rho gH \left (1 — \frac > > \right )$.

$V = \sqrt <2 \cdot 9,8 8>\frac <3,14 \cdot 10^<-4>> <4>= 9,8 \cdot 10^ <-4>м^ <3>/с$;
$\Delta p = 10^ <3>\cdot 9,8 \cdot 0,5 + 10^ <3>\cdot 9,8 \cdot 8 \left ( 1 — \frac <10^<-8>> <625 \cdot 10^<-8>> \right ) = 83,3 \cdot 10^ <3>н/м^<2>$.

Источник

Сопло фонтана дающего вертикальную струю высотой 5 м имеет форму усеченного конуса

1 3 0 1 . Тело с плотностью r падает с высоты H в жидкость с плотностью r ₁ ( r r ₁). Найти глубину погружения и время подъема тела на поверхность. решение

1 3 0 2 . Через небольшую пробоину в трюме судна бьет струя воды. Один человек не в состоянии преодолеть силу струи, чтобы закрыть отверстие доской. Однако, когда с помощью товарища доска была наложена, человек оказался в состоянии удержать доску. Почему? решение

1 3 0 3 . На гладкой горизонтальной поверхности стоит широкий сосуд с водой. Уровень воды в сосуде – h , вес сосуда с водой Q . В боковой стенке у дна сосуда имеется заткнутое отверстие с площадью S . Найти, при каком значении коэффициента трения между дном и поверхностью сосуд придет в движение, если вынуть затычку? решение

1 3 0 4 . Сосуд с жидкостью падает с ускорением a g . Как меняется давление p с глубиной? решение

1 3 0 5 . Из трубы сечением S ₁ бьет вертикально вверх струя воды. Найти сечение струи на высоте h над отверстием трубы. Расход воды из трубы равен Q . решение

1 3 0 6 . Труба сечением S образует прямоугольное колено. По трубе течет поток газа со скоростью v . Плотность газа r . Найти силу давления газа на трубу. решение

1 3 0 7 . В дне цилиндрического сосуда диаметром D имеется малое круглое отверстие диаметром d . Найти зависимость скорости v ₁ понижения уровня воды в сосуде от высоты h этого уровня. решение

1 3 0 8 . Площадь поршня в шприце равна S ₁, а площадь отверстия на выходе S ₂. Ход поршня равен l . На поршень действует сила F . Найти скорость и время вытекания воды из шприца, если он расположен горизонтально, а скорость поршня постоянна. решение

1 3 0 9 . Сопло фонтана, дающего вертикальную струю высотой H , имеет форму усеченного конуса, сужающегося кверху. Диаметр верхнего сечения – d , нижнего – D , высота сопла – h . Найти расход воды Q за 1 c и избыточное давление D p в нижнем сечении (насколько это давление больше атмосферного). решение

1310. Найти скорость течения углекислого газа по трубе, если известно, что через 30 мин через поперечное сечение трубы протекает масса газа 0,51 кг. Плотность газа 7,5 кг/м 3 . Диаметр трубы 2 см. решение

следующая десятка >>>

Смотрите новый сайт В. Грабцевича по физике, а также шутки про школу.

Источник

Сопло фонтана дающего вертикальную струю высотой 5 м имеет форму усеченного конуса

Движение тел в жидкостях и газах

Одной из важнейших задач аэро- и гидродинамики является исследование движения твердых тел в газе и жидкости, в частности изучение тех сил, с которыми среда действует на движущееся тело. Эта проблема приобрела особенно большое значение в связи с бурным развитием авиации и увеличением скорости движения морских судов.

На тело, движущееся в жидкости или газе, действуют две силы (равнодействующую их обозначим R), одна из которых (Rx) направлена в сторону, противоположную движению тела (в сторону потока), — лобовое сопротивление, а вторая (Ry) перпендикулярна этому направлению — подъемная сила (рис. 55).

Если тело симметрично и его ось симметрии совпадает с направлением скорости, то на него действует только лобовое сопротивление, подъемная же сила в этом случае равна нулю. Можно доказать, что в идеальной жидкости равномерное движение происходит без лобового сопротивления. Если рассмотреть движение цилиндра в такой жидкости (рис. 56), то картина линий тока симметрична как относительно прямой, проходящей через точки А и В, так и относительно прямой, проходящей через точки С и D, т. с. результирующая сила давления на поверхность цилиндра будет равна нулю.

Иначе обстоит дело при движении тел в вязкой жидкости (особенно при увеличении скорости обтекания). Вследствие вязкости среды в области, прилегающей к поверхности тела, образуется пограничный слой частиц, движущихся с меньшими скоростями. В результате тормозящего действия этого слоя возникает вращение частиц и движение жидкости в пограничном слое становится вихревым. Если тело не имеет обтекаемой формы (нет плавно утончающейся хвостовой части), то пограничный слой жидкости отрывается от поверхности тела. За телом возникает течение жидкости (газа), направленное противоположно набегающему потоку. Оторвавшийся пограничный слой, следуя за этим течением, образует вихри, вращающиеся в противоположные стороны (рис. 57).

Лобовое сопротивление зависит от формы тела и его положения относительно потока, что учитывается безразмерным коэффициентом сопротивления Сx, определяемым экспериментально:

где r — плотность среды; v — скорость движения тела; S — наибольшее поперечное сечение тела.

Составляющую Rx можно значительно уменьшить, подобрав тело такой формы, которая не способствует образованию завихрения.

Подъемная сила может быть определена формулой, аналогичной (33.1):

где Су — безразмерный коэффициент подъемной силы.

Для крыла самолета требуется большая подъемная сила при малом лобовом сопротивлении (это условие выполняется при малых углах атаки a (угол к потоку); см. рис. 55). Крыло тем лучше удовлетворяет этому условию, чем больше величина К=Су/Сx называемая качеством крыла. Большие заслуги в конструировании требуемого профиля крыла и изучении влияния геометрической формы тела на коэффициент подъемной силы принадлежат «отцу русской авиации» Н. Е. Жуковскому (1847—1921).

6.1. Полый железный шар (r =7,87 г/см3) весит в воздухе 5 Н, а в воде (r’ = 1 г/см3) — 3 Н. Пренебрегая выталкивающей силой воздуха, определить объем внутренней полости шара. [139 см3]

6.2. Бак цилиндрической формы площадью основания S = 1 м2 и объемом V = 3 м 3 заполнен водой. Пренебрегая вязкостью воды, определить время t, необходимое для опустошения бака, если на дне бака образовалось круглое отверстие площадью S1 =10 см2.

6.3. Сопло фонтана, дающего вертикальную струю высотой H = 5 м, имеет форму усеченного конуса, сужающегося вверх. Диаметр нижнего сечения d1 = 6 см, верхнего — d2 = 2 см. Высота сопла h = 1 м. Пренебрегая сопротивлением воздуха в струе и сопротивлением в сопле, определить: 1) расход воды в 1 с, подаваемой фонтаном; 2) разность Dр давления в нижнем сечении и атмосферного давления. Плотность воды r =1 г/см3. [1) d2/4 = 3,1 х 10-3 м3/с; 2) Dp = pgh + pgH (1– d /d =58,3 кПа]

6.4. На горизонтальной поверхности стоит цилиндрический сосуд, в боковой поверхности которого имеется отверстие. Поперечное сечение отверстия значительно меньше поперечного сечения самого сосуда. Отверстие расположено на расстоянии h1 = 64 см ниже уровня воды в сосуде, который поддерживается постоянным, и на расстоянии h2 = 25 см от дна сосуда. Пренебрегая вязкостью воды, определить, на каком расстоянии по горизонтали от сосуда падает на поверхность струя, вытекающая из отверстия. [80 см]

6.5. В широком сосуде, наполненном глицерином (плотность r =1,2 г/см3), падает с установившейся скоростью 5 см/с стеклянный шарик (r’ = 2,7 г/см3) диаметром 1 мм. Определить динамическую вязкость глицерина. [1,6 Па × с]

6.6. В боковую поверхность цилиндрического сосуда, установленного на столе, вставлен на высоте h1 = 5 см от его дна капилляр внутренним диаметром d = 2 мм и длиной l = 1 см. В сосуде поддерживается постоянный уровень машинного масла (плотность r = 0,9 г/см3 и динамическая вязкость h = 0,1 Па×с) на высоте h2 = 80 см выше капилляра. Определить, на каком расстоянии по горизонтали от конца капилляра падает на поверхность стола струя масла, вытекающая из отверстия.

6.7. Определить наибольшую скорость, которую может приобрести свободно падающий в воздухе (r=1,29 г/см3) стальной шарик (r’ = 9 г/см3) массой m = 20 г. Коэффициент Сх принять равным 0,5. [94 см/с]

Такой подход к объективной реальности резко ограничивает сферу рассмотрения физических явлений и, конечно, предсказательность теории. Это подтверждает и анализ результатов эксперимента Саньяка, выполненный с позиций теории относительности. По нему возможно проведение только одного варианта эксперимента, в полном соответствии со схемой (74), и при этом вся конструкция должна вращаться в вакууме. Световые лучи, двигаясь навстречу друг другу и ударяясь о зеркала S1, S3, изменяют свой импульс и свою скорость (?), что и регистрируется интерферометром К. Никаких других изменений и предложений по новым экспериментам на основе анализа (рис. 74) сделать не представляется возможным.

По Г. Лоренцу, тяготеющий эфир, образующий пространство внутри полого диска при его вращении, сепарируется и располагается так, что более тяжелые частицы прилегают к ободу вращающегося диска, легкие же перемещаются к оси вращения. Поэтому структура пространства внутри вращающегося полого диска меняется и возникает локальное тяготение, направленное от оси к ободу. Одновременно сам эфир внутри полости увлекается диском. Световой луч, летящий навстречу вращению, встречает более сжатую зону эфира и ускоряется, а летящий по направлению вращения — менее сжатую и замедляется. Именно это явление фиксируется интерферометром.

Полученная из анализа эксперимента по теории Г. Лорентца физическая картина расширяет представление о сути явления, позволяет предсказать новые эксперименты и сделать следующие выводы:

• все окружающее пространство образовано телесным эфиром;

• частицы телесного эфира являются самотяготеющими и сепарируются полым вращающимся диском;

• сепарация эфира образует внутри полого вращающегося диска локальное гравитационное поле;

• гравитационное притяжение передается близкодействием от частицы к частице, т.е. так, как это предполагал И. Ньютон [20], хотя это не вытекает из его теории.

Появление в полости вращающегося диска локального гравитационного поля может быть проверено экспериментально:

• видоизменением эксперимента Саньяка;

• по изменению частоты света, движущегося как в направлении притяжения, так и против;

• по изменению скорости течения времени внутри диска;

• по изменению линейных размеров тел, помещенных в локальное гравитационное поле, а также другими экспериментами.

Прежде чем приступить к описанию экспериментов, подтверждающих образование локального гравитационного поля, замечу, что отрицание эфира имело своим последствием постулирование принципиальной невозможности локализации гравитационного поля, а, следовательно, и его экранирования [61,122-125]. Потомкам судить, какой вред был нанесен этим запретом науке, но до сих пор физики-теоретики и экспериментаторы даже помыслить не могут об экранировании гравитационных полей.

А теперь снова об эксперименте Саньяка. Теория относитель-ности не предполагает никаких изменений в его проведении. Теория эфира такие изменения предполагает в следующем виде (рис. 75). Внутри полого диска А, способного вращаться, устанавливается неподвижный диск-короб В, к стенке которого крепятся зеркала S1, S2, S3, отражающие световые лучи и полупрозрачная пластинка G, которая расщепляет луч света на два луча, идущих в противоположных направлениях. В остальном схема эксперимента (рис. 75) ничем не отличается от схемы эксперимента Саньяка (рис. 74) и от эксперимента по локализации гравиполя (рис. 22). Возникает вопрос: Можно ли обнаружить вращение диска А, находясь внутри покоящегося короба В?

Ответ теории относительности отрицателен. Поскольку диск В не вращается, световые лучи, двигаясь от зеркала к зеркалу, не изменяют своего импульса и, следовательно, двигаются с постоянной скоростью. Интерференционная картина изменяться не будет. Вращение внешнего диска обнаружить невозможно.

По теории Г. Лорентца, вращающийся диск А приводит во вращение и сепарирует эфир во всем объеме диска, включая неподвижный короб В. Конечно, сепарация в неподвижном коробе в диске должна происходить медленнее, но и в этом случае световые лучи будут идти навстречу друг другу с различными скоростями, и при сложении их интерференционная картина будет изменяться, свидетельствуя о вращении наружного диска. Эффект будет усилен, если зеркала S1, S2, S3, укрепить на неподвижной основе внутри диска А в вакууме.

Таким образом, измененный эксперимент Саньяка не просто зафиксирует возможность определения состояния наружного диска приборами, находящимися внутри него, но и позволит однозначно выяснить, какая из релятивистских теорий (Г. Лорентца или А. Эйнштейна) более адекватно отражает природные процессы.

Известно, что фотоны света, движущиеся от гравитирующего тела, уменьшают частоту волны — так называемое красное смещение, и наоборот, — движущиеся к гравитирующему телу фотоны увеличивают свою частоту, т.е. испытывают фиолетовое смещение. Это свойство фотонов можно использовать для доказательства появления локального гравитационного поля внутри полого, вращающегося диска, заменив систему зеркал Саньяка источником света и его приемником на ободе или на оси.

Источник

5.3. Сопло фонтана, дающего вертикальную струю высотой имеет форму усеченного

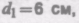
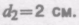
конуса, сужающегося вверх. Диаметр нижнего сечения верхнего — Вы-

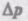
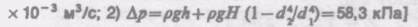
сота сопла h=1 м. Пренебрегая сопротивлением воздуха в струе и сопротивлением в сопле, определить: 1) расход воды в 1 с, подаваемой фонтаном; 2) разность давления в нижнем сечении и атмосферного давления. Плотность воды [1)

5.4. На горизонтальной поверхности стоит цилиндрический сосуд в боковой поверхности которого имеется отверстие. Поперечное сечение отверстия значительно меньше поперечного сечения самого сосуда. Отверстие расположено на расстоянии 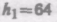см ниже уровня воды в сосуде,

который поддерживается постоянным, и на расстоянии 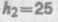см от дна сосуда. Пренебрегая

вязкостью воды, определить, на каком расстоянии по горизонтали от сосуда падает на поверхность струя, вытекающая из отверстия. [80 см]

5.5. В широком сосуде, наполненном глицерином (плотность падает с устано-

вившейся скоростью 5 см/с стеклянный шарик диаметром 1 мм. Определить

динамическую вязкость глицерина. [1,6 Па. с]

5.6. В боковую поверхность цилиндрического сосуда, установленного на столе, вставлен на высоте 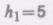см от его дна капилляр внутренним диаметром d=2 мм и длиной В сосуде

поддерживается постоянный уровень машинного масла (плотность 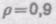г/см 3 и динамичес-

кая вязкость на высоте см выше капилляра. Определить, на каком

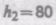
расстоянии по горизонтали от конца капилляра падает на поверхность стола струя масла, вытекающая из отверстия.

5.7. Определить наибольшую скорость, которую может приобрести свободно падающий в воз­духе стальной шарик массой _m = 20 г. Коэффициент принять

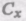
равным

Глава 7

Элементы специальной (частной) теории относительности

§ 34. Преобразования Галилея. Механический принцип относительности

— классической механике справедлив механический принцип относительности (принцип относительности Галилея): законы дианамики одинаковы во всех инерциальных систе­мах отсчета.

Для его доказательства рассмотрим две системы отсчета: инерциальную систему К (с координатами 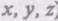), которую условно будем считать неподвижной, и систему

(с координатами 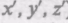), движущуюся относительно К равномерно и прямолинейно со

скоростью 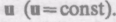Отсчет времени начнем с момента, когда начала координат

обеих систем совпадают. Пусть в произвольный момент времени t расположение этих систем друг относительно друга имеет вид, изображенный на рис. 58. Скорость ■ направлена вдоль радиус-вектор, проведенный из

Найдем связь между координатами произвольной точки А в обеих системах. Из I рис. 58 видно, что

(34.1)

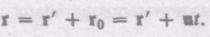
Уравнение (34.1) можно записать в проекциях на оси координат:

(34.2) |

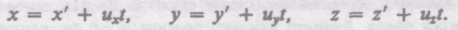
Уравнения (34.1) и (34.2) носят название преобразовавши координат Галилея.

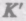
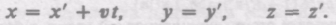
В частном случае, когда система движется со скоростью т вдоль положительного направления оси х системы К (в начальный момент времени оси координат совпадают), преобразования координат Галилея имеют вид

В классической механике предполагается, что ход времени не зависит от относи­тельного движения систем отсчета, т. е. к преобразованиям (34.2) можно добавить еще одно уравнение:

(34.3)

Записанные соотношения справедливы лишь в случае классической механики

а при скоростях, сравнимых со скоростью света, преобразования Галилея заменяются

более общими преобразованиями Лоренца* (§ 36).

Продифференцировав выражение (34.1) по времени (с учетом (34.3)), получим уравнение

(34.4)

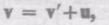
которое представляет собой правило сложения скоростей в классической механике. Ускорение в системе отсчета К

Таким образом, ускорение точки А в системах отсчета 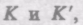движущихся друг

относительно друга равномерно и прямолинейно, одинаково:

(34.5)

Следовательно, если на точку А другие тела не действуют (а=0), то, согласно (34.5), и 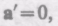т. е. система является инерциальной (точка движется относительно нее

равномерно и прямолинейно или покоится).

Таким образом, из соотношения (34.5) вытекает подтверждение механического принципа относительности: уравнения динамики при переходе от одной инерциальной

* Х. Лоренц (1853—1928) — нидерландский физик-теоретик.

системы отсчета к другой не изменяются, т. е. являются инвариантными по отношению преобразованиям координат. Галилей обратил внимание, что никакими механичес­кими опытами, проведенными в данной инерциальной системе отсчета, нельзя устано­вить, покоится ли она или движется равномерно и прямолинейно. Например, сидя в каюте корабля, движущегося равномерно и прямолинейно, мы не можем определить, покоится корабль или движется, не выглянув в окно.

Источник