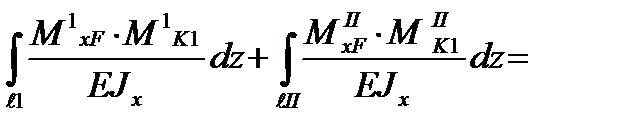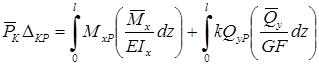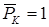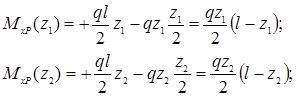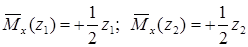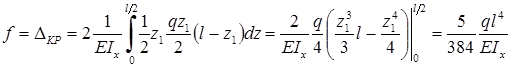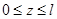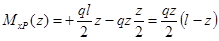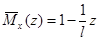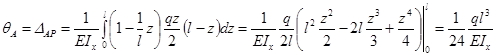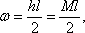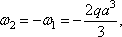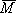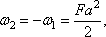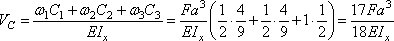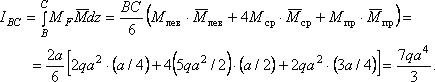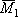Решение задач интегралом мора примеры

Вычисление интеграла Мора пример

Интеграл Мора определяет величину перемещения произвольного сечения балки. Физический смысл интеграла Мора – работа единичной силы на перемещение ее точки приложения от заданной нагрузки. То есть, отсюда следует, если при вычислении интеграла Мора результат получается положительным, то это значит, что направление единичной силы совпадает с направлением искомого перемещения. В противном случае – направление единичной силы и искомого перемещения прямо противоположны.

Этапы решения задач для определения перемещения с помощью интеграла Мора.

1. Определяются опорные реакции и составляется уравнение для изгибающих моментов М_хF от заданной нагрузки F = F₁, F₂, ….F_n.

2. Освобождается конструкция от заданной нагрузки F, к такой свободной конструкции прикладывается единичный силовой фактор (сила равна единице или момент равен единице) в направлении искомого перемещения (линейного или углового) в заданной точке К.

3. Определяются заново опорные реакции от единичного силового фактора и составляется уравнение изгибающего момента М_к1 от этого единичного силового фактора.

4. Вычисляется перемещение искомой точки К с помощью интеграла Мора.

Определить прогиб балки посередине пролета и угол поворота поперечного сечения на левой опоре. Жесткость балки на изгиб — EJ_x, длина — ℓ.

Используя интеграл Мора для решения нужно составить выражения для изгибающих моментов для каждого характерного участка. Для данной конструкции характерных участка — два.

1. Определяем реакции опор R_A и R_B c помощью уравнений равновесия

2. Для изгибающего момента на первом участке М_хF = F/2 ∙ z, (0 ≤ z ≤ ℓ/2);

на втором участке М_хF = F/2 ∙ z — F(z — ℓ/2), (ℓ/2 ≤ z ≤ ℓ);

3. Освобождаем балку от заданной нагрузки F и прикладываем силу, равную единице, в направлении искомого прогиба в середине пролета балки.

4. Определяем заново реакции опор R_A и R_B.

5. Для изгибающих моментов от единичного силового фактора запишем:

для первого участка — М_к1 = 1/2 ∙ z, (0 ≤ z ≤ ℓ/2);

на втором участке — М_к2 = 1/2 ∙ z — (z — ℓ/2), (ℓ/2 ≤ z ≤ ℓ);

6. Определим прогиб в середине пролета балки:

δ_kF=

Учитывая, что эпюры М_xF и M_K симметричны можно увеличить первое слагаемое в два раза и отбросить второе.

7. Для определения угла поворота поперечного сечения в точке А также освобождаем исходную балку от нагрузки и прикладываем единичный силовой фактор — изгибающий момент, который равен единице, в направлении искомого перемещения.

8. Для новой расчетной схемы из условия равновесия балки определяем реакции опоры.

Условие равновесия (сумма проекций всех сил = 0) на вертикальную ось.

9. Изгибающий момент от действия сосредоточенного момента в т. А:

М_А1 = 1 — R_A ∙ z = 1 — z /ℓ (0 ≤ z ≤ ℓ)

10. Определяем угол поворота левого крайнего сечения:

φ_АF=

Положительное значение угла поворота означает, что выбранное направление единичного силового фактора совпадает с направлением истинного искомого перемещения.

Метод Мора оптимально применять для криволинейных брусьев малой кривизны.

Для стальной балки подобрать сечение из двух рядом стоящих швеллеров, если [σ] = 160 МПа. Определить прогиб балки посередине и угол поворота на правом конце.

q = 50 кН/м; F = 15кН; М = 15 кНм.

Проверка: R_А — F – q 6 + R_B = 0; 157,5 – 15 — 50 · 6 + 157,5 = 0

→ Q_С = R_А — q· 2 = 157,5 – 50 ·2 =57,2 кН

← Q_С = -R_В + q· 4 = -157,5 + 50· 4 =42,5 кН

→ М_С = М + R_А 2 — q ·2 ·1 = 15 + 157,5 · 2 – 50 ·2 · 1 = 230 кНм

М_мах = М + R_А 2,85 — F· 0,85 — q ·2,85 ·1,425 = 15 +157,5 — F 2,85– 150,83 – 50 · 2,85 · 1,425 = 248 кНм- F

Учитывая, что Q_Z = R_A — F – q (2+ z) = 0, то z = = 0,85 м.

Из условия прочности по нормальным напряжениям

σ = / W_x [σ]

σ = = = 1550 = 1550

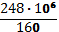
Сечение состоит из двух рядом стоящих швеллеров W_x = 2 W_x

Момент сопротивления одного швеллера W_x1= W_x/2 = 1550/2 = 775

По ГОСТ 8240-97 два швеллера № 40 W_x= 761 , J_x = 15220 , A = 61,5

В опасном сечении напряжение

σ = = 162,9 Мпа [σ]

Перегрузка П = 100% = 1,8%. Допустимая величина.

Прочность балки обеспечена.

Определяем прогиб сечения D и угол поворота сечения К, используя уравнения начальных параметров.

Выбираем начало координат в точке О – крайней левой точке балки. Определяем прогиб посередине пролета при z = 3 м.

ЕJ_x y_D = ЕJ_x y₀ + ЕJ_{x 0} 3 + M + R_Ay – F – q

Правило знаков — как у изгибающего момента.

Находим начальные параметры y_0, из условия закрепления концов балки.

При z = 0, y_A = y₀ = 0, _A = ₀ y_В = 0. Следовательно

ЕJ_x y_В = ЕJ_{x 0} 6 + M + R_Ay – F – q = 0

ЕJ_{x 0} = -513,3 кН м,

ЕJ_x y_D = — 513,3 2,85 + 15 + 157,5 – 15 – 50 = -1046,5 кНм 3

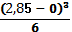
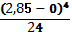
y_D = — = — 17,2 мм

Знак минус показывает то, что балка прогибается вниз.

Находим угол поворота сечения К при z = 7 м.

ЕJ_{x К} — 513,3+ 15 + 157,5 – 15 – 50 = 404,6 кНм 2

_К Место для формулы. = 0,00665 рад.

Источник

Определение прогибов и углов поворотов методом Мора

Интеграл Мора позволяет определять прогибы и углы поворота заданного сечения балки, используя интегральное исчисление. Хотя данный метод предпочтительнее метода начальных параметров, он неудобен из-за необходимости вычисления интеграла. Из интеграла Мора был получен удобное для практического применения правило Верещагина, при котором не нужно вычислять интегралы, а только нужно находить площадь и центр тяжести эпюр.

Получение формулы интеграла Мора

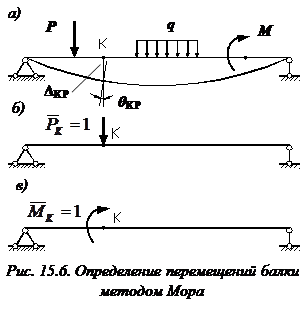
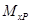
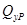
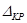
Рассмотрим балку, изображенную на рис. 15.6, а. Обозначим и , соответственно, изгибающий момент и поперечную силу, возникающие в заданной балке от действующей на нее группы нагрузок P. Пусть требуется определить прогиб балки () в точке K.

Введем в рассмотрение вспомогательную балку (та же балка, но нагруженная только единичной силой либо единичным изгибающим моментом). Нагрузим ее только одной силой (рис. 15.6, б). Единичную силу приложим в точке K, где нужно определить прогиб.

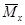
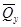
Внутренние усилия, возникающие во вспомогательной балке, обозначим и .

Воспользуемся теперь теоремой о взаимности работ, согласно которой работа внешних сил, приложенных к вспомогательной балке на соответствующих перемещениях заданной балки равна взятой с обратным знаком работе внутренних сил заданной балки на соответствующих перемещениях вспомогательной балки. Тогда .

При определении перемещений в балке, как правило, можно пренебрегать влиянием поперечной силы, ( не учитывать второе слагаемое).

Тогда, учитывая, что , окончательно получим формулу интеграла Мора : .

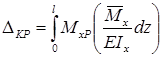
Определение перемещений по формуле интеграла Мора часто называют определением перемещений методом Мора , а саму формулу – интегралом Мора .

Входящие в интеграл Мора изгибающие моменты берутся в произвольном поперечном сечении и поэтому представляют собой аналитические функции от текущей координаты z.

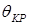
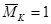
Заметим, что если мы хотим в этой же точке K определить угол поворота поперечного сечения (), то нам необходимо к вспомогательной балке приложить не единичную силу, а единичный момент (рис. 15.6, в).

порядок вычисления перемещений методом Мора:

· к вспомогательной балке в той точке, где требуется определить перемещение, прикладываем единичное усилие. При определении прогиба прикладываем единичную силу , а при определении угла поворота – единичный момент ;

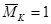
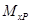
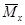
· для каждого участка балки составляем выражения для изгибающих моментов заданной () и вспомогательной () балок;

· вычисляем интеграл Мора для всей балки по соответствующим участкам;

· если вычисленное перемещение имеет положительный знак, то это означает, что его направление совпадает с направлением единичного усилия. Отрицательный знак указывает на то, что действительное направление искомого перемещения противоположно направлению единичного усилия.

Вычисление интеграла Мора пример

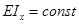
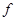
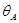
Пусть для шарнирно опертой балки постоянной изгибной жесткости , длиной l, нагруженной равномерно распределенной нагрузкой интенсивностью q (рис. 15.7, а), требуется определить прогиб посредине пролета () и угол поворота на левой опоре ().

определение прогиба с помощью интеграла Мора

В том месте, где нам нужно определить прогиб, к вспомогательной балке прикладываем единичную силу (рис. 15.7, б).

Записываем выражения для изгибающих моментов для каждого из двух участков () заданной и вспомогательной балок:

.

.

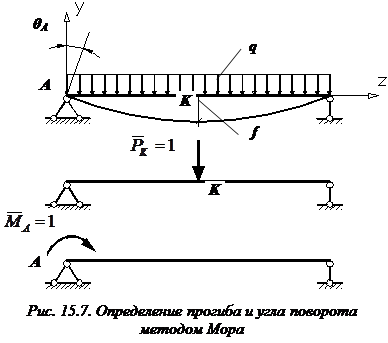
Вычисляем интеграл Мора . Учитывая симметрию балки, получим:

.

Определение угла поворота методом Мора

Нагружаем вспомогательную балку единичным моментом , прикладывая его в том месте, где мы ищем угол поворота (рис. 15.7, в).

Записываем выражения для изгибающих моментов в заданной и вспомогательной балках только для одного участка ():

;

.

Тогда интеграл Мора будет иметь вид:

.

Положительный знак в выражении для угла поворота поперечного сечения балки указывает на то, что поворот сечения происходит по направлению единичного момента .

Источник

метод Верещагина

Определить перемещение точки К балки (см. рис.) при помощи интеграла Мора.

1) Составляем уравнение изгибающего момента от внешней силы M_F.

2) Прикладываем в точке К единичную силу F = 1.

3) Записываем уравнение изгибающего момента от единичной силы .

Определить перемещение точки К балки по способу Верещагина.

2) Прикладываем в точке К единичную силу.

; ;

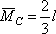
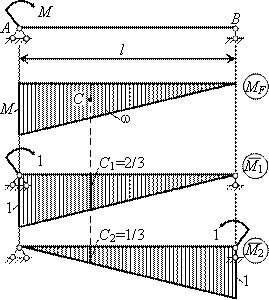
Определить углы поворота на опорах А и В для заданной балки (см. рис.).

Строим эпюры от заданной нагрузки и от единичных моментов, приложенных в сечениях А и В (см. рис.). Искомые перемещения определяем с помощью интегралов Мора

,

, которые вычисляем по правилу Верещагина.

C₁ = 2/3, C₂ = 1/3,

а затем и углы поворота на опорах А и В

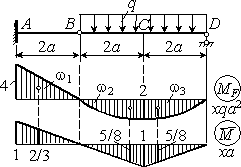
Определить угол поворота сечения С для заданной балки (см. рис.).

Определяем опорные реакции R_A=R_B,

, , R_A = R_B = qa.

Строим эпюры изгибающего момента от заданной нагрузки и от единичного момента, приложенного в сечении С, где ищется угол поворота. Интеграл Мора вычисляем по правилу Верещагина. Находим параметры эпюр

C₂ = —C₁ = -1/4,

а по ним и искомое перемещение

.

Определить прогиб в сечении С для заданной балки (см. рис.).

1. Построение эпюр изгибающих моментов.

Эпюра M_F (рис. б)

ВЕ: , ,

, R_B + R_E = F, R_E = 0;

АВ: , R_А = R_В = F; , .

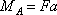
Вычисляем моменты в характерных точках , M_B = 0, M_C = Fa и строим эпюру изгибающего момента от заданной нагрузки.

Эпюра (рис. в).

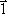
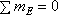
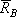
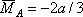
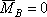
В сечении С, где ищется прогиб, прикладываем единичную силу и строим от нее эпюру изгибающего момента, вычисляя сначала опорные реакции ВЕ — , , = 2/3; , , = 1/3, а затем моменты в характерных точках , , .

2. Определение искомого прогиба. Воспользуемся правилом Верещагина и вычислим предварительно параметры эпюр и :

,

.

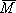
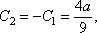
Определить прогиб в сечении С для заданной балки (см. рис.).

Строим эпюры изгибающих моментов от заданной нагрузки и от единичной силы, приложенной в точке С. Пользуясь правилом Верещагина, вычисляем параметры эпюр ,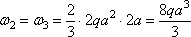

.

Определить прогиб в сечении С для заданной балки (см. рис.).

1. Построение эпюр изгибающих моментов.

, , R_A = 2qa,

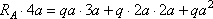
, R_A + R_D = 3qa, R_D = qa.

Строим эпюры изгибающих моментов от заданной нагрузки и от единичной силы, приложенной в точке С.

2. Определение перемещений. Для вычисления интеграла Мора воспользуемся формулой Симпсона, последовательно применяя ее к каждому из трех участков, на которые разбивается балка.

Участок АВ:

Участок ВС:

Участок СD:

.

Определить прогиб сечения А и угол поворота сечения Е для заданной балки (рис. а).

1. Построение эпюр изгибающих моментов.

Эпюра М_F (рис. в). Определив опорные реакции

, , R_B = 19qa/8,

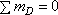
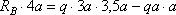
, R_D = 13qa/8, строим эпюры поперечной силы Q и изгибающего момента М_F от заданной нагрузки.

Эпюра (рис. д). В сечении А, где ищется прогиб, прикладываем единичную силу и строим от нее эпюру изгибающего момента.

Эпюра (рис. е). Эта эпюра строится от единичного момента, приложенного в сечении Е, где ищется угол поворота.

2. Определение перемещений. Прогиб сечения А находим, пользуясь правилом Верещагина. Эпюру М_F на участках ВС и CD разбиваем на простые части (рис. г). Необходимые вычисления представляем в виде таблицы.

Источник