Механика грунтов. Лекция №4
Раздел 1. Механика грунтов Лекция №2: Физико-механические свойства грунтов основания. Методы их исследования. Основные и производные характеристики Строительная классификация грунтов Лекция №3. Механические свойства грунта Деформируемость грунтов. Понятие об упругих и пластических деформациях. Лабораторные и полевые методы исследований сжимаемости грунтов. Лекция №4 Прочность грунтов. Предельное сопротивление грунтов сдвигу. Закон Кулона. Теория прочности Кулона-Мора. Характеристики прочности грунтов. Исследование прочности грунтов в приборах прямого одноплоскостного среза и в приборах трехосного сжатия. Водопроницаемость грунтов. Закон ламинарной фильтрации Дарси. Характеристики водопроницаемости: коэффициент фильтрации и начальный градиент напора и методы их определения. Исследование фильтрационных свойств грунтов в трубке Каменского и в компрессионно-фильтрационных приборах.
Прочность грунтов Прочность – такое предельное значение напряжения сжатия или растяжения, после достижения которого материал теряет свою сплошность, образуются трещины отрыва или сдвига и он распадается на части. Процесс называют хрупким разрушением. Некоторые материалы (битум, лед) теряют прочность без видимого нарушения сплошности (неограниченные пластические деформации переходящие в течение) Особенности разрушения материалов (хрупкое или пластическое) зависят не только от преобладающих в них структурных связях но и от скорости нагружения. Под прочностью в широком смысле понимают способность сопротивляться разрушению или развитию больших пластических деформаций приводящих к большим искажениям формы Применительно к песчаным грунтам в 1773 г. французским ученым Ш.Кулоном было установлено что их разрушение происходит за счет сдвига одной части грунта по другую. Сопротивление растяжению в этих грунтах практически отсутствует. Эта концепция распространилась и на пылевато-глинистые грунты. Однако процесс разрушения в них значительно сложнее, за счет водно-коллойдных и цементационных связей, которые обеспечивают некоторое сопротивление растяжению.
Сопротивление грунтов сдвигу зависит от плотности сложения, влажности, гранулометрического и минерального состава, напряженного состояния. Характеристики сопротивления сдвигу грунтов рассматриваются как прочностные показатели и всегда определяются экспериментально. Одноосные испытания (сжатие) В основном проводятся для скальных грунтов. Образцы цилиндрической формы диаметром 40…45 мм. Условия аналогичные определению деформационных характеристик, только нагрузка доводится до полного разрушения образца. В результате определяют ПРОЧНОСТЬ ОБРАЗЦА ГРУНТА НА ОДНООСНОЕ СЖАТИЕ Fпр – предельное разрушающее усилие А – площадь поперечного сечения образца Для различных скальных грунтов может изменятся в широких пределах: Мел, слабые известняки и песчанники – 1…5 МПа Базальты, габбро, мрамор – 250…300 МПа и более Сопротивление растяжению (Rp – прочность образца грунта на одноосное растяжение) – определяется непосредственными испытаниями прямыми или косвенными методами. Но с достаточной для инженерных целей точностью можно принять как
Одноплоскостной сдвиг Используется сдвиговой прибор Верхняя, подвижная часть Плоскость среза 
Нижняя, неподвижная часть Образец грунта Индикатор горизонтальных перемещений Прикладывается вертикальное усилие F которое вызывает напряжение Затем при постоянном значении =const к верхней части прибора ступенями (5% от ) прикладывается горизонтальное усилие T. В плоскости среза возникает касательное напряжение Обычно образец выдерживается до полной стабилизации горизонтальных перемещений от этой нагрузки, после чего прикладывают новую ступень нагрузки. По мере увеличения увеличивается интенсивность горизонтальных перемещений и при некотором предельном значении 
дальнейшее перемещение образца происходит без увеличения сдвигающего напряжения
Предельное значение , называется сопротивлением сдвигу . Испытания проводятся для разных значений 3 > 2 > 1 =const
Закон Кулона График зависимости сопротивления сдвигу песчаного грунта от нормального напряжения может быть представлен отрезком прямой и зависимость выражена уравнением (1) (1) — угол внутреннего трения f – коэффициент внутреннего трения При испытании пылевато-глинистых грунтов получают более сложную криволинейную зависимость. Сопротивление сдвигу обуславливается не только силами трения, но и связностью грунта, т.е. сложными процессами нарушения связей между частицами. Зависимость сопротивления сдвигу от нормального напряжения представляется уравнением (2) (2) С – удельное сцепление пылевато-глинистого грунта, характеризующее его связность. Параметры и с лишь условно могут быть названы углом внутреннего трения и удельным сцеплением, т.к. физика процесса разрушения сложнее. А уравнения (1) и (2) называют законом Кулона
Сопротивление сдвигу при сложном нагружении. Теория прочности Кулона-Мора Схема одноплоскостного сдвига, это частный случай разрушения грунта в основании сооружений. Рассмотрим более сложное нагружение: К граням элементарного объема приложены главные напряжения Если увеличивать 1 оставляя постоянной 3 в определенный момент произойдет сдвиг по некоторой площадке, наклоненной к горизонтальной плоскости, промежуточное главное напряжение 2 будет действовать параллельно этой площадке и никак не влияя на сопротивление грунта сдвигу. Положение площадки скольжения неизвестно в отличии от одноплоскостного сдвига (зазор между подвижной и неподвижной частями прибора) Принимают что на площадке скольжения выполняется условие (1) и (2)
Для касательного и нормального напряжения на наклонной площадке известны выражения (3) Эти напряжения в предельном состоянии будут связаны выражением (2) (4) Положение площадок скольжения можно определить из условия (5) В предельном состоянии в каждой точке грунта имеются две сопряженные площадки скольжения, наклоненной под углом (45 — /2) к линии действия максимального и (45 + /2) – минимального главного напряжения
Приведенные выше положения наглядно иллюстрируются с помощью графического построения кругов напряжений Мора для предельного состояния. Образец испытывается при постоянном значении минимального главного напряжения 3 = const и при некотором значении максимального главного напряжения 1 наступает его разрушение (формируются площадки скольжения) Прямая ОА, построенная как касательная к кругу Мора, и проходящая через точку Е (отрезок ОЕ = С) будет соответствовать зависимости (4) (4) Для любой точки на круге напряжений и площадки не находящейся в предельном состоянии угол отклонения будет всегда меньше максимального угла отклонения max = Прямая ОА не может пересекать круг напряжений.
Источник
1.8 Критерий Кулона-Мора
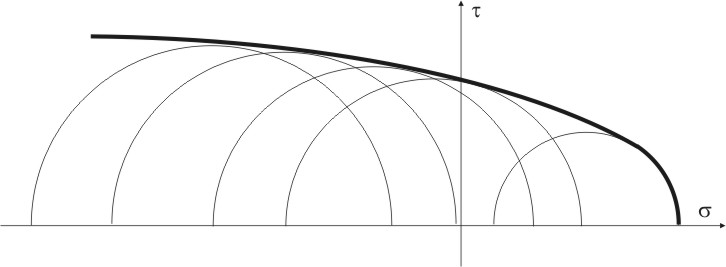
Рассмотренные критерии пластичности применимы для материалов одинаково сопротивляющихся растяжению и сжатию. Однако, ряд материалов обладает разной прочностью при растяжении и сжатии. Критерий Кулона-Мора основан на предположении, что прочность зависит, главным образом, от величины и знака наибольшего 1 и наименьшего3 главных напряжений. Если при некоторых 1 и 3 возникает текучесть, то круг Мора, построенный на этих напряжениях, соответствует предельному состоянию материала. Меняя соотношение между 1 и 3, получим семейство предельных кругов. Огибающая этих кругов определяет сочетания нормальных и касательных напряжений, при которых возникает текучесть материала (рис 9.4).
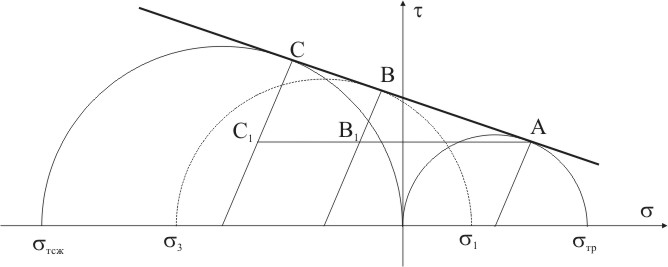
Для точного построения огибающей необходимо выполнить большое количество экспериментов при различных напряженных состояниях. На практике ограничиваются минимальным количеством испытаний для наиболее просто реализуемых напряженных состояний. Огибающую можно с достаточной степенью точностью заменить прямой касательной к кругам Мора построенным для растяжения с диаметром равным пределу текучести при растяжении т р и для сжатия — с диаметром равным пределу текучести при сжатии т сж. Следовательно, для построения схематизированной огибающей достаточно провести испытания образцов материала при одноосном растяжении и при одноосном сжатии. С достаточной степенью точности огибающая заменяется касательной к кругам Мора, соответствующих результатам этих испытаний (рис. 9.5).
Это позволяет найти зависимость между главными напряжениями рассматриваемого напряженного состояния 1 и 3 и эквивалентным напряжением экв при равноопасном одноосном растяжении. В точка касания огибающей с тремя кругами восстановим перпендикуляры, которые совпадают с радиусами кругов, а через точку А проведем горизонтальную прямую. Из подобия треугольников ABB1 и ACC1, следует
Подставим эти выражения в соотношение (1) и после преобразований получим условие тукучести:
Обозначим , тогда условие текучести принимает вид:
Следовательно, эквивалентное напряжение:
При двухосном напряженном состоянии σ3 = 0, следовательно, условие текучести принимает вид:
Учитывая, что для бруса в опасном сечении действуют нормальные напряжения σ и касательные напряжения τmax, тогда главные напряжения:
Подставим выражение (3) в соотношение (2) после преобразований получим условие текучести для бруса:
Эквивалентное напряжение для бруса:
1.9 Условия текучести при двухосном напряженном состоянии
Проанализируем условия текучести при различных критериях для двуосного напряженного состояния. Условия текучести имеют следующий вид:
а) по критерию максимального главного напряжения:
б) по критерию максимальной главной деформации:
в) по критерию суммарной энергии деформации:
σ1 2 + σ2 2 + 2μσ1σ2 = σтр 2
г) по критерию максимальных касательных напряжений:
д) по критериям энергии деформации сдвига и интенсивности напряжений:
Представим эти соотношения в прямоугольных координатах «u-v», которые повернуты относительно координат «σ1-σ2» на 45 против часовой стрелки. Для этого подставим в условия текучести:
Тогда при различных критериях для двуосного напряженного состояния и при равенстве пределов текучести на растяжение и сжатие (σтр = σтсж = σт) условия текучести принимают вид.
а) по критерию максимального главного напряжения:
б) по критерию максимальной главной деформации:
в) по критерию суммарной энергии деформации:
Это уравнение эллипса с центром в начале координат, малой полуосью и большой полуосью ;
г) по критерию максимальных касательных напряжений:
д) по критерию энергии деформации сдвига и интенсивности напряжений:
Это уравнение эллипса с центром в начале координат, малой полуосью и большой полуосью .
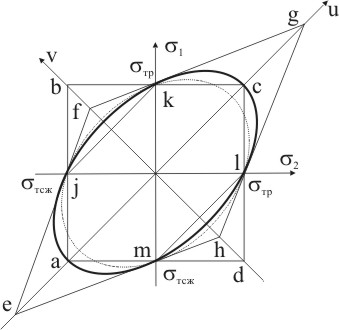
Построим приведенные соотношения в прямоугольных координатах «σ1-σ2» (рис. 9.6).
Фигура Критерий статической прочности
abcd Критерий максимального главного напряжения
efgh Критерий максимальной главной деформации
ajkclm Критерий максимальных касательных напряжений
эллипс (сплошная линия) Критерий энергии деформации сдвигу
эллипс (пунктирная линия) Критерий суммарной энергии деформации
Каждая из фигур означает, что для соответствующего критерия текучесть не наступит до тех пор, пока точка со значениями σ1, σ2 не выйдет за пределы области ограниченной фигурой. Сравнение областей ограниченных различными фигурами показывает, что наименьшая область ограничена шестиугольником ajkclm, который соответствует критерию максимальных касательных напряжений. Можно заметить, что в том случае, когда главные напряжения σ1, и σ2 одновременно растягивающие или сжимающие, то области ограниченные шестиугольником ajkclm и квадратом abcd ( 1-ая и 3-ая четверти прямоугольной системы координат) совпадают. В том случае, когда одно из главных напряжений растягивающее, а другое сжимающее, то область, ограниченная шестиугольником ajkclm меньше области ограниченной квадратом abcd. Это означает, что при прогнозе текучести по критерию максимальных касательных напряжений текучесть наступит раньше, чем по критерию наибольших главных напряжений. Эллипс, ограничивающий область соответствующую, как критерию энергии деформации сдвига, так и критерию интенсивности напряжений огибает шестигранник, соответствующий критерию наибольших касательных напряжений. Таким образом, по критерию энергии деформации сдвига текучесть наступит при больших значениях главных напряжений σ1, и σ2, чем по критерию наибольших касательных напряжений. По критерию максимальной главной деформации область ограничена ромбом диагонали которого совпадают с осями координат u-v, развернутыми относительно исходной системы координат σ1-σ2 на 45.
В заключении следует отметить, что прогноз текучести по шести рассмотренным критериям предельного состояния только по трем критериям (критерий наибольших касательных напряжений, критерий энергии сдвига и критерий интенсивности напряжений) согласуются с результатами эксперимента. Кроме того только эти три критерия позволяют утверждать, что текучесть не наступит при всестороннем растяжении или сжатии в условиях отсутствия касательных напряжений, что также подтверждается экспериментом.
Источник