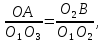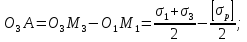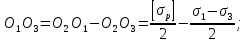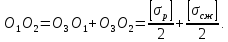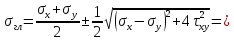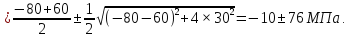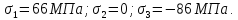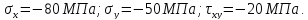Предельная огибающая кругов мора

Предельная огибающая кругов мора

Паспортом прочности горной породы является кривая, огибающая предельные круги напряжений Мора в координатах нормальных и касательных напряжений. Предельный круг Мора соответствует предельному напряженному состоянию, достигаемому при данном соотношении наибольшего и наименьшего главных нормальных напряжений, и имеет радиус с координатами центра

На черт. 2 приведены наиболее характерные круги Мора, огибающая их кривая и обозначены основные параметры, определяемые по паспорту прочности:

предельное сопротивление срезу (сцепление С₀) при отсутствии нормальных напряжений, т.е. и соответствующий угол внутреннего трения нормальных напряжений, т.е. и соответствующий угол внутреннего трения (коэффициент внутреннего трения ) — постоянные параметры:

условное сцепление С при различных напряжениях , и соответствующий угол внутреннего трения (коэффициент внутреннего трения ) — переменные параметры.

1 — круг одноосного растяжения; 2 — круг одноосного сжатия; 3 — круг объемного сжатия; nn — касательная к огибающей в точке ее пересечения с осью mm -касательная к огибающей в любой точке на ней

1. Метод построения паспорта прочности по данным определения пределов
прочности при объемном сжатии, одноосном сжатии и растяжении

1.1. Для построения паспорта прочности используют результаты определения пределов прочности при объемном сжатии не менее чем при трех (в пределах заданного диапазона напряжений) различных значениях бокового давления p.

1.2. По совокупности парных значений и в координатах строят семейство полуокружностей радиусами с координатами центров ( ).

1.3. К семейству полуокружностей по п. 1.2 добавляют полуокружности радиусами и с координатами центров (- ; 0) и ( ; 0), где — предел прочности при одноосном растяжении по ГОСТ 21153.3-85, разд. 2 или 4; — предел прочности при одноосном сжатии по ГОСТ 21153.2-84, разд. 1 по ГОСТ 21153.3-85, разд. 4.

2. Метод построения паспорта прочности по данным определения пределов
прочности при срезе со сжатием, одноосном сжатии и растяжении

2.1. По совокупности парных значений и , определенных по ГОСТ 21153.5-88, в координатах наносят точки 1, 2 и 3, соответствующие углам в соответствии с черт. 3.

Источник

6.2.3. Критерий Мора. Паспорт прочности породы

Из эксперимента следует, что для упруго-пластичных пород кривая предельного состояния в широком диапазоне нормальных напряжений носит сублинейный характер, т.е. лежит ниже прямой (6.9). Эта особенность учитывается в теории Кулона-Мора, являющейся дальнейшим развитием теории Кулона-Навье.

Критерий Мора основан на построении огибающей предельных кругов в координатной плоскости — . Круги Мора для трехосного напряженного состояния подробно рассматривались в главе 4. По прежнему будем считать, что выполняется условие — и большой круг, изображенный на рис. 4.9, соответствует предельному состоянию породы.

Согласно предположению Мора напряженные состояния, отвечающие точкам, лежащим вне круга, соответствуют разрушению породы, внутри круга – не разрушенной породе. Причем предельное состояние породы не зависит от промежуточного напряжения — . Такое предположение находится в полном согласии с положением, доказанным в главе 4, что дозволенные состояния в случае трехосного напряженного состояния соответствуют области внутри большого круга и вне малых кругов. Таким образом, по результатам трехосных испытаний породы на прочность с — можно построить семейство предельных кругов, проходящих через точки — , и провести непрерывную огибающую этих кругов.

Н а рис. 6.5 показаны ряд предельных кругов в области сжимающих напряжений и непрерывная монотонно возрастающая кривая, являющаяся огибающей предельных кругов. Рассмотрим следующий случай. При воздействии на породу гидростатического давления не должно происходить ее разрушение. Действительно, в этом случае все главные напряжения равны, и поэтому круг, построенный на этих напряжениях, стягивается в точку, расположенную на оси нормальных напряжений. Следовательно, точки напряженного состояния — , соответствующие действию гидростатического давления, будут всегда находиться ниже предельной кривой.

В области растягивающих напряжений ситуация иная. При действии на породу возрастающих растягивающих напряжений всегда наступит момент, когда произойдет разрушение породы. Поэтому в этой области в качестве предела прочности можно принять предел прочности породы при всестороннем равномерном растяжении — . Таким образом, огибающая предельных кругов будет исходить из точки — .

При стягивании круга Мора в точку касательная к нему становится перпендикулярной оси нормальных напряжений. Следовательно, первая производная от огибающей предельных кругов Мора в точке — стремится к положительной бесконечности. Вообще говоря, разумным становится требование, чтобы первая производная была непрерывной и положительной. Из физических соображений это означает, что порода не испытывает фазовых превращений при давлениях, соответствующих реальным горным давлениям при ведении разработок. И, наконец, предельный вид огибающей должен удовлетворять уравнению (6.9). Легко убедиться, что подходящее уравнение огибающей предельных кругов Мора будет вида — , где – постоянная.

Согласно критерию Мора разрушение породы может быть двух видов: в области сжимающих напряжений и в области сжимающих напряжений и примерно равных им по модулю растягивающих напряжений (напряженное состояние, близкое к чистому сдвигу) разрушение происходит по площадкам скольжения в результате достижения предельных касательных напряжений; в области растягивающих напряжений – в результате отрыва.

Заметим, что практически не возможно осуществить всестороннее равномерное растяжение, поэтому огибающую предельных кругов практически строят из точки, соответствующей пределу прочности породы при одностороннем растяжении — , и продолжают ее по соответствующему кругу (рис. 6.5). Это не приводит к заметной ошибке, так как .

В горной практике огибающая предельных кругов Мора носит название паспорта прочности горной породы. Основное назначение паспорта прочности заключается в том, чтобы по известному трехосному напряженному состоянию ответить на вопрос о возможном разрушении породы.

Р ассмотрим следующий пример. Паспорт прочности известняка имеет вид , где и в МПа. Следует ответить на вопрос: «Выдержит ли известняк трехосное напряженное состояние: = 20 МПа, = 70 МПа, = 160 МПа?» Согласно предположению Мора промежуточное напряжение не влияет на предельное состояние известняка. Поэтому в системе координат — строим график паспорта прочности и окружность с центром на оси нормальных напряжений — и радиусом — (рис. 6.6). Как следует из рис. 6.6, окружность пересекла график паспорта прочности. Следовательно, еще до момента создания заданного напряженного состояния произойдет разрушение породы.

Источник

8.6. Теория прочности Мора

В отличие от изложенных выше теорий, теория Мора основывается не на гипотезах, а на экспериментальных данных. Зависимость между прочностными свойствами материала и видом напряженного состояния выводится и обосновывается с использованием кругов напряжений Мора. Для этого выбирается некоторое напряженное состояние, и одновременно увеличиваются его составляющие. 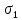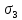Когда напряженное состояние станет предельным, на напряжениях и строится соответствующий им круг Мора. Среднее напряжение не учитывается. Опыт показывает, что ошибка при этом не превышает 10–15 %. Строится ряд таких кругов, соответствующих различным напряженным состояниям (рис. 8.2). Огибающая этих кругов, форма которой зависит от свойств материала, является его механической характеристикой.

Если огибающая предельных кругов Мора построена, то для ответа на вопрос, является ли напряженное состояние, характеризующееся главными напряжениями, предельным, и для оценки прочности материала следует построить для и круг напряжений в опасной точке материала. Прочность будет обеспечена, если он целиком лежит внутри огибающей. Для нахождения коэффициента запаса следует определить, во сколько раз необходимо увеличить и , чтобы круг касался огибающей.

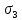
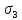
Для построения действительной огибающей предельных кругов Мора потребовалось бы опытным путем исследовать всевозможные напряженные состояния. Это неосуществимая задача, поэтому на практике действительную огибающую заменяют прямыми касательными лишь к двум предельным кругам, соответствующим опытам на одноосное растяжение и сжатие.

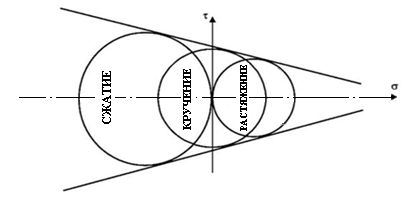
Рис. 8.2. Огибающая кругов Мора для различных напряженных

Условие прочности для промежуточного напряженного состояния с главными напряжениями и предельным кругом Мора с центром в точке О₃ (рис. 8.3) получим из следующих геометрических соотношений.

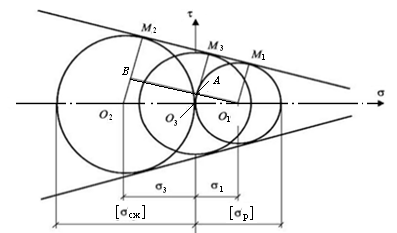
Проведем прямые О₁М₁, О₂М₂ и О₃ М₃,соединяющие центры предельных кругов Мора и точки их касания с предельной прямой, а также отрезок BО₁ параллельный М₁М₂. Из подобия ∆О₁О₂В и ∆О₁О₃А получим следующие зависимости:

Рис. 8.3. Схема для получения условия прочности Мора

Учитывая эти обозначения, преобразуем последнее равенство к виду:

Тогда получим условие прочности по теории Мора:

Если материал одинаково сопротивляется растяжению и сжатию, т. е. , теория прочности Мора совпадает с третьей теорией.

Выводы. Таким образом, разрушение материала может происходить путем отрыва одной части от другой и путем среза. Как правило, разрушение путем отрыва происходит хрупко, без заметных остаточных деформаций. Разрушение путем среза сопровождается пластическими деформациями. Поэтому первую и вторую теории можно применять для оценки прочности хрупких материалов, а третью и четвертую – пластических. Теория Мора позволяет учитывать разное сопротивление материала растяжению и сжатию.

8.7. Пример расчета

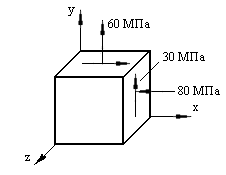
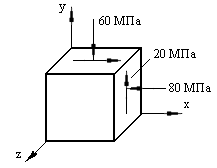
Задача 1. В опасной точке нагруженной детали напряженное состояние оказалось таким, как указано на схеме (рис. 8.4). Проверить прочность детали по третьей теории прочности, если [σ] = 160 МПа.

Рис. 8.4. Схема опасной точки

Задача 2. В опасной точке нагруженной детали напряженное состояние оказалось таким, как указано на схеме (рис. 8.5). Проверить прочность материала по третьей и четвертой теориям прочности, если σ_р = σ_сж и [σ] = 160 МПа.

Рис. 8.5. Схема опасной точки

.

Задача 3. В опасной точке нагруженной детали напряженное состояние оказалось таким, как указано на схеме (рис. 8.6). Проверить прочность материала по четвертой теории прочности, если [σ] = 90 МПа.

Рис. 8.6. Схема опасной точки

Источник