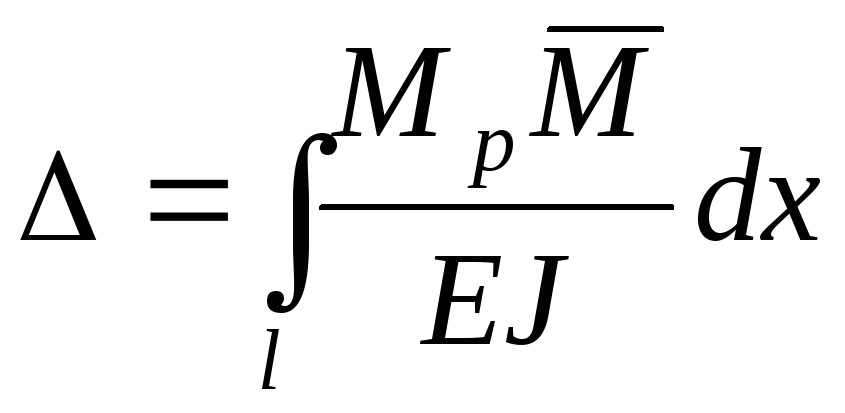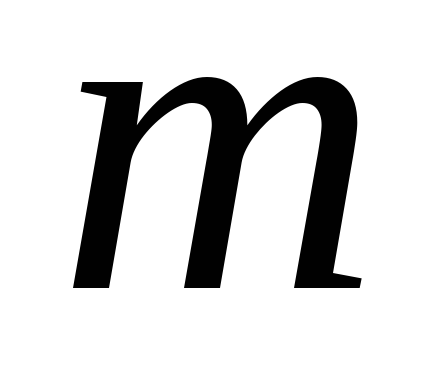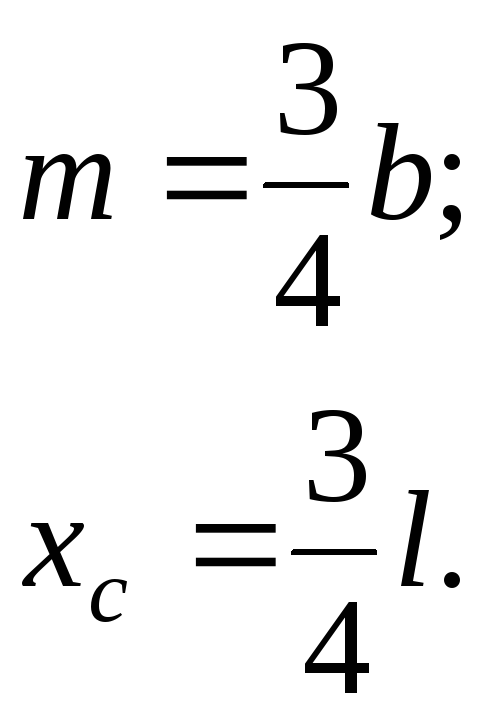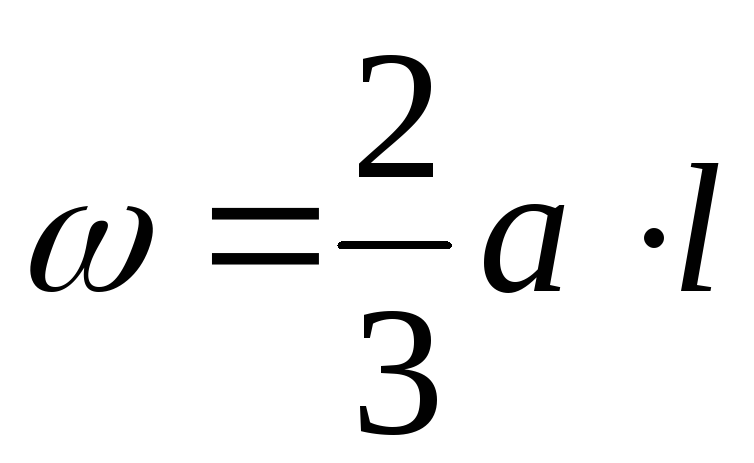Правило мора перемножение эпюр

Правило мора перемножение эпюр

Калькулятор умножения эпюр объясняет как получить произведение эпюр, необходимое для вычисления интеграла Мора. Обычно используется правило Верещагина или правило Симпсона-Корноухова.
Укажите длину участка и значения по краям эпюр. Для криволинейной эпюры дополнительно укажите интенсивность распределенной нагрузки q («+» вниз, «-» вверх, «0» — если нагрузки нет).
Внизу Вы найдете результат и подробное объяснение, как именно множить Ваши эпюры.

Произведение эпюр по правилу Верещагина

Произведение двух эпюр равно площади первой эпюры, умноженной на значение на второй эпюре напротив центра тяжести первой

$$\int f(z) \cdot y(z) dz =\Omega \cdot y_c $$

В том случае, если площадь или центр тяжести на первой эпюре посчитать сложно, ее обычно разбивают на более простые фигуры.

В нашем случае имеем:
— прямоугольник 6×12, площадь 72, центр тяжести посредине, значение напротив центра тяжести 13;
— треугольник 6×30, площадь 90, центр тяжести на 2/3 длины, значение напротив центра тяжести 3.67;
— парабола 6×54, площадь 216 (высота параболы считается по формуле qL^2/8, и не важно она горизонтально расположена или под углом, а площадь = 2/3 ширины на высоту), центр тяжести посредине, значение напротив центра тяжести 13;
$$\int f(z) = -72\cdot13+90\cdot3.67+216\cdot13=2202$$знак «-» ставим, если первая эпюра и значение на второй расположены по разные стороны стержня.

Произведение эпюр по правилу Симпсона

$$\int f(z) \cdot y(z) dz = \frac< l><6>(y_ \cdot f_+4*y_ \cdot f_+y_ \cdot f_) = $$ $$ = \frac<6><6>(-12\cdot41+4*57\cdot13+18\cdot-15) = 2202$$ где $l$ — длина участка, в скобках $y$ и $f$ — значения на эпюрах слева, посредине участка и справа.

Источник

2. Правило Мора-Верещагина (графический способ вычисления интеграла Мора)

Кроме метода начальных параметров существует эффективный универсальный метод определения перемещений в балках, рамах и упругих конструкциях произвольной конфигурации – метод Мора. Упругое перемещение (либо прогиб, либо угол поворота сечения) определяется по формуле:

, (1.3)

где – изгибающий момент от заданной нагрузки;– изгибающий момент от единичной силы, приложенной в той точке, в которой определяется перемещение.

Упрощение операций интегрирования возможно для конструкций с прямолинейной осью постоянной жесткости и основано на том, что эпюры от единичных усилий на прямолинейных участках оказываются линейными. Рассматривая эту процедуру применительно к участку балки, преобразуем интеграл Мора с учетом этой особенности. На рис. 1.3 сверху показан участок балки с эпюрой общего вида, а внизу эпюра , представляющая собой линейную функцию. В результате несложного расчета (подробности смотри в учебнике) установлено, что интеграл произведения двух функций и численно равен площади эпюры , умноженной на величину момента, взятого с эпюры в сечении, соответствующем центру тяжести эпюры .

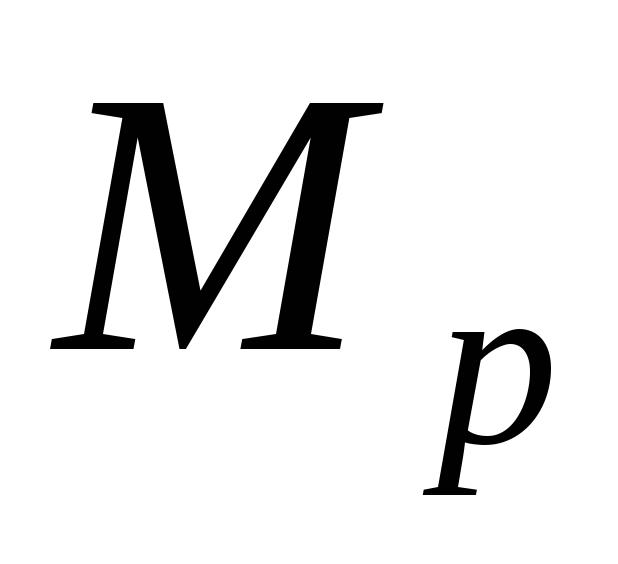
. (1.4)

Если балка имеет несколько участков по длине, формула Верещагина будет иметь вид

, (1.5)

где – площадь эпюры моментов от внешней нагрузки (грузовой эпюры); – ордината единичной эпюры под центром тяжести грузовой эпюры; – число участков по длине балки.

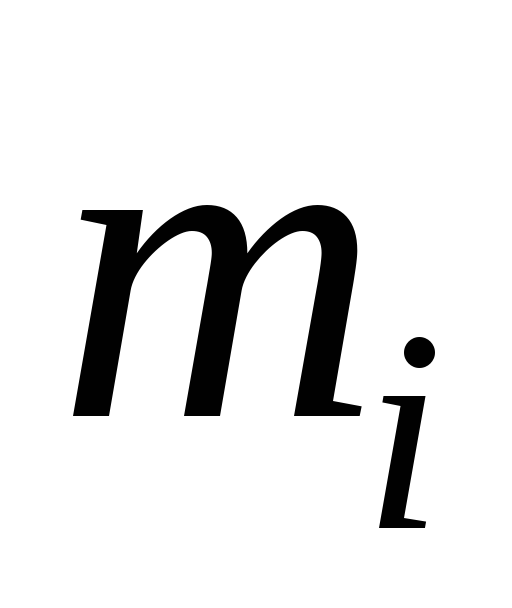
При пользовании этой формулой надо уметь вычислять площади и координаты центров тяжести основных фигур: прямоугольника, прямолинейного треугольника и криволинейного треугольника. Минимально необходимые справочные данные приведены в табл. 1.1. Процедуру графического вычисления называют «перемножением» эпюр.

Эпюры и

эпюры ,

тяжести

Эпюры и

эпюры ,

тяжести

Примечания: 1. Все кривые в табл. 1.1 – квадратные параболы. 2. При «перемножении» эпюр одного знака их произведение положительно. 3. При «перемножении» эпюр разных знаков их произведение отрицательно.

В случае, если эпюра тоже линейная, операция перемножения обладает свойством коммутативности: безразлично, умножается ли площадь грузовой эпюры на ординату единичной или площадь единичной на ординату грузовой.

Рассмотрим на примере расчетной схемы, показанной на рис. 1.4, порядок решения задач при определении перемещения с помощью правила Мора-Верещагина. Определим прогиб в точке .

Чтобы построить эпюры и ,можно не определять опорные реакции: достаточно сосчитать момент на опореот нагрузки на консоли, построить эпюру на консоли, а затем соединить прямой линией значениеM на опореB с нулем на опореA.

В соответствии с формулой (1.5)

.

Источник

2. Правило Мора-Верещагина (графический способ вычисления

Кроме метода начальных параметров существует эффективный универсальный метод определения перемещений в балках, рамах и упругих конструкциях произвольной конфигурации – метод Мора. Упругое перемещение (либо прогиб , либо угол поворота сечения ) определяется по формуле:

где – изгибающий момент от заданной нагрузки; – изгибающий момент от единичной силы, приложенной в той точке, в которой определяется перемещение.

Упрощение операций интегрирования возможно для конструкций с прямолинейной осью постоянной жесткости и основано на том, что эпюры от единичных усилий на прямолинейных участках оказываются линейными. Рассматривая эту процедуру применительно к участку балки, преобразуем интеграл Мора с учетом этой особенности. На рис. 1.3 сверху показан участок балки с эпюрой общего вида, а внизу эпюра , представляющая собой линейную функцию. В результате несложного расчета (подробности смотри в учебнике) установлено, что интеграл произведения двух функций и численно равен площади эпюры , умноженной на величину момента, взятого с эпюры в сечении, соответствующем центру тяжести эпюры .

– обобщённое перемещение: либо прогиб , либо угол поворота . Если вычисляем прогиб, то в этой точке по направлению искомого прогиба к ненагруженной балке прикладываем единичную силу и строим эпюру . Если вычисляем угол поворота , то к ненагруженной балке в этой точке по направлению искомого углового перемещения прикладываем единичный момент и строим эпюру .

Если балка имеет несколько участков по длине, формула Верещагина будет иметь вид

где – площадь эпюры моментов от внешней нагрузки (грузовой эпюры); – ордината единичной эпюры под центром тяжести грузовой эпюры; – число участков по длине балки.

При пользовании этой формулой надо уметь вычислять площади и координаты центров тяжести основных фигур: прямоугольника, прямолинейного треугольника и криволинейного треугольника. Минимально необходимые справочные данные приведены в табл. 1.1. Процедуру графического вычисления называют «перемножением» эпюр.

Источник