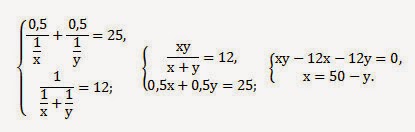Первая труба заполняет бассейн за один день

Две трубы наполняют бассейн за 3 часа 36 минут, а одна первая труба наполняет бассейн за 6 часов. За сколько часов наполняет бассейн одна вторая труба?

Пусть объем бассейна равен 1. Обозначим и — скорости наполнения бассейна первой и второй трубой, соответственно. Две трубы наполняют бассейн за 3 часа 36 минут:

По условию задачи одна первая труба наполняет бассейн за 6 часов, то есть Таким образом,

Тем самым, вторая труба за час наполняет 1/9 бассейна, значит, вторая труба наполняет этот бассейн за 9 часов.

Приведем другое решение.

Первая труба за час наполняет 1/6 бассейна, значит, за 3 ч 36 мин = 3,6 часа она заполнит 0,6 бассейна. Следовательно, вторая труба за 3,6 часа заполнит 0,4 бассейна. Поэтому весь бассейн она заполнит за время 3,6:0,4 = 9 часов.

Источник

Первая труба заполняет бассейн за один день

Первая труба заполняет бассейн за 7 часов, а две трубы вместе — за 5 часов 50 минут. За сколько часов заполняет бассейн одна вторая труба?

Первая труба заполняет бассейн за 7 часов, две трубы вместе — за за 5 часов 50 минут то есть за 35/6 часа. Это значит, что за час первая труба заполняет 1/7 бассейна, а две трубы — 6/35 бассейна. При совместной работе производительности складываются, поэтому производительность второй трубы равна разности общей производительности и производительности первой трубы: бассейна в час. Тем самым, вторая труба заполняет бассейн за 35 часов.

То же самое решение составлением уравнения.

Поскольку первая труба заполняет бассейн за 7 часов, она заполняет одну седьмую бассейна в час. Пусть x — время, за которое вторая труба заполняет бассейн, в час она заполнит 1/х часть бассейна. Известно, что две трубы, работая одновременно, заполнили бассейн за 35/6 часа. Значит, в час они заполняли 6/35 бассейна. Тогда получаем:

Можно даже проще. Найдём время заполнения каждой трубы t, объём выполненной работы V и выполненную работу A (в нашем случае она будет равна 1, так как они заполнили 1 бассейн). Итак, время второй трубы обозначим за x, так как она нам не известна. А первая труба заполняет бассейн за 7 часов. Тогда объём работы 1 трубы будет равен 1/7. Аналогично 2 труба 1/х. Это мы нашли объём выполненной работы каждой трубой по отдельности. Нам известно что 2 трубы вместе выполнили данную работу за 5 часов 50 минут (то есть 5 целых 5/6). Тогда общий объём равен 6/35 (просто переведите 5 целых 5/6 в неправильную дробь и разделите 1 на на неё). Отсюда следует, что:

Источник

Математика по полочкам

Готовимся к экзамену по математике за период обучения на II ступени общего среднего образования

21. Задачи на совместную работу

МАТЕРИАЛ ДЛЯ ПОВТОРЕНИЯ

Задачи на работу

В таких задачах всегда присутствуют одни и те же величины, их три:
— первая величина — это время, за которое выполняется та или иная работа. Обозначают время буквой t.
— вторая величина — объём работы: сколько сделано деталей, налито воды, вспахано полей и так далее. Обозначим объем буквой О.
— третья величина — производительность. По сути, это скорость работы. Обозначим производительность буквой П.

Скорость любой работы, т.е. производительность можно определить, как объём работы, сделанной за какое-то время.
Получим формулу для производительности: П = О : t.

Пример. Токарь делает 5 деталей в час. Сколько деталей он сделает за 7 часов?

Пример. Красная Шапочка и Волк очень любят пирожки. Волк может съесть 24 пирожка за 4 часа, а Красная Шапочка — 35 пирожков за 7 часов. У Волка в корзинке 30 пирожков, а у Красной Шапочки — 20. Кто съест свои пирожки раньше, если они начали есть одновременно?

Задачи на совместную работу

Пример. Одна труба может наполнить бассейн за четыре часа. Вторая — за шесть часов. За какое время заполнится бассейн, если обе трубы включить одновременно?

Так как трубы работают вместе, складывают их производительности.
Для первой трубы, которая заполняет 1 бассейн за 4 часа: П = О:t = 1:4, т.е. за час первая труба заполнит 1/4 бассейна.
Для второй трубы: П = О:t = 1:6, т.е. вторая труба заполнит за час 1/6 бассейна.
Вместе, при совместной работе, трубы заполнят за час: 1/4 + 1/6 = 5/12 — две трубы за 1 час.
Объём работы 1 бассейн. Совместная производительность 5/12 бассейна в час.
t = О:П = 1 : 5/12 = 12/5 = 2,4 (ч.)
Ответ:2,4 часа.

УПРАЖНЕНИЯ

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

3. Два экскаватора роют траншею. Работая отдельно, первый может вырыть траншею за 10 дней, второй — за 16 дней. За сколько дней они выроют траншею, работая совместно?

4. Водоем заполняется первой трубой за 5 ч, а второй трубой за 4 ч. За сколько часов наполнится водоем, если будут одновременно работать две трубы?

5. Две наборщицы должны были набрать по 120 страниц каждая. Вторая наборщица набирала за 1 ч на 5 страниц меньше, чем первая, поэтому закончила работу на 2 ч позже. Сколько страниц в час набирала первая наборщица?

6. Две бригады рабочих должны по плану изготовить 240 деталей. Первая бригада работала 6 ч, а вторая — 5 ч. Сколько деталей в час изготавливала каждая бригада, если первая делала на 4 детали в час меньше, чем вторая?

Источник

Через первую трубу бассейн наполняется за 20 часов ,а через вторую за 30 часов .За сколько часов наполнится бассейн через

Ответ или решение 2

Если первая труба наполняет весь бассейн за 20 часов, то за 1 час она наполняет 1/20 бассейна.

Если вторая труба наполняет весь бассейн за 30 часов, то за 1 час она наполняет 1/30 бассейна.

Тогда вместе эти трубы за один час выльют в бассейн 1/20 + 1/30 = (3 + 2)/60 = 5/60 = 1/12 бассейна.

А весь бассейн заполнят за 1/(1/12) = 12 часов.

Ответ: через обе трубы бассейн наполнится за 12 часов.

Для решения задачи, за сколько часов наполнится бассейн через две трубы, сначала нужно определить какую часть бассейна наполняет каждая труба в единицу времени.

Определение производительности труб

Введем следующие обозначения:

N1 — часть бассейна, заполняемая первой трубой за час;
N2 — часть бассейна, заполняемая второй трубой за час;
N1 + N2 — часть бассейна, наполняемая двумя трубами за час;

Рассчитав эти величины, мы определим общую производительность двух труб вместе, то есть часть бассейна, которую они вместе заполняют за час.

Расчет времени заполнения бассейна двумя тубами

1. Часть бассейна, заполняемая первой трубой за час:
N1 = 1/20;
2. Часть бассейна, заполняемая второй трубой за час:
N2 = 1/30;
3. Часть бассейна, заполняемая двумя трубами за час:
N1 + N2 = 1/20 + 1/30 = 3/60 + 2/60 = 5/60 = 1/12;

Тогда, время. необходимое, чтобы наполнить бассейн двумя трубами вместе, определится делением целого (полный бассейн принят за единицу) на его часть, заполняемую в 1 час.
4. Время t, необходимое для заполнения бассейна:
t = 1 / (1/12) = 12 часов;
Ответ: Бассейн наполнится через обе трубы за 12 часов.

Источник

Первая труба заполняет бассейн за один день

Первый и второй насосы наполняют бассейн за 9 минут, второй и третий — за 14 минут, а первый и третий — за 18 минут. За сколько минут эти три насоса заполнят бассейн, работая вместе?

Наименьшее общее кратное чисел 9, 14 и 18 равно 126. За 126 минут первый и второй, второй и третий, первый и третий насосы (каждый учтен дважды) заполнят 14 + 9 + 7 = 30 бассейнов. Следовательно, работая одновременно, первый, второй и третий насосы заполняют 15 бассейнов за 126 минут, а значит, 1 бассейн за 8,4 минуты.

Приведём другое решение.

За одну минуту первый и второй насосы заполнят 1/9 бассейна, второй и третий — 1/14 бассейна, а первый и третий — 1/18 бассейна. Работая вместе, за одну минуту два первых, два вторых и два третьих насоса заполнят

бассейна.

Тем самым, они могли бы заполнить бассейн за 21/5 минуты или за 4,2 минуты. Поскольку каждый из насосов был учтен два раза, в реальности первый, второй и третий насосы, работая вместе, могут заполнить бассейн за 8,4 минуты.

Приведем алгебраическое решение Тимура Алиева.

Пусть x — производительность первого насоса, y — производительность второго насоса, z — производительность третьего насоса. Тогда

Сложив уравнения, получим

Тогда при совместной работе всех трех насосов время заполнения бассейна составит минуты.

Источник