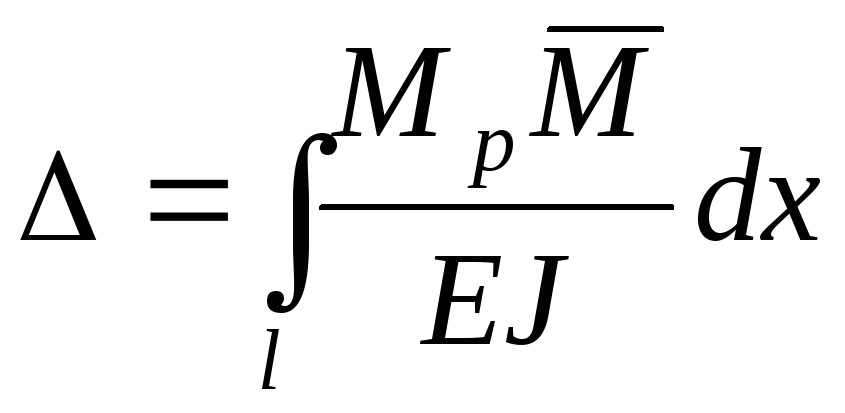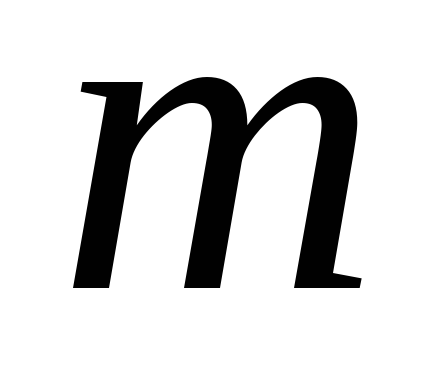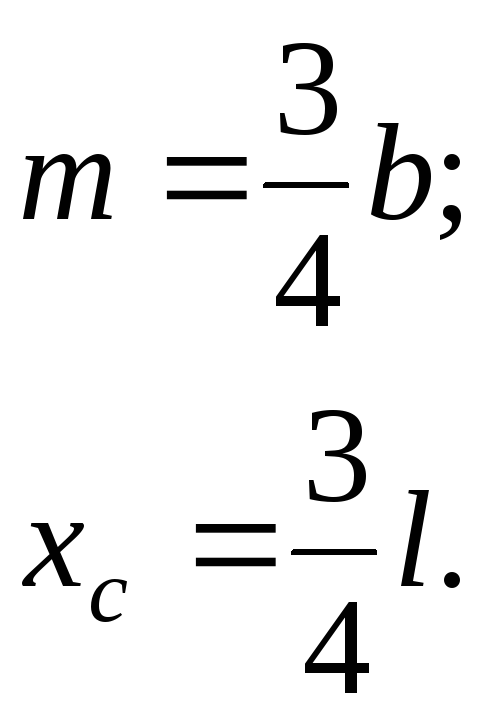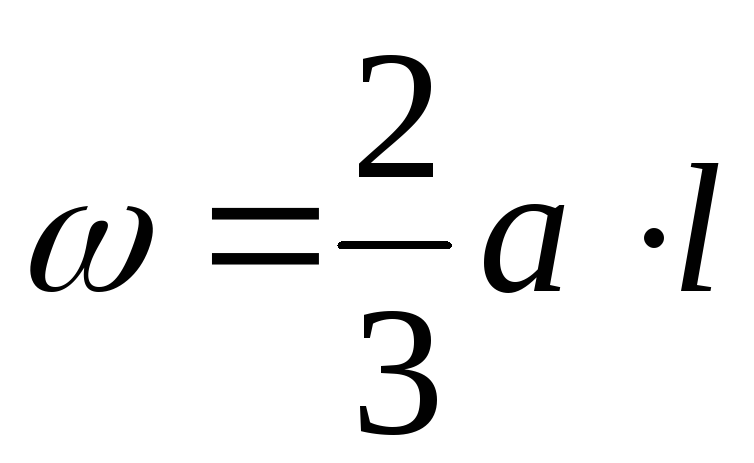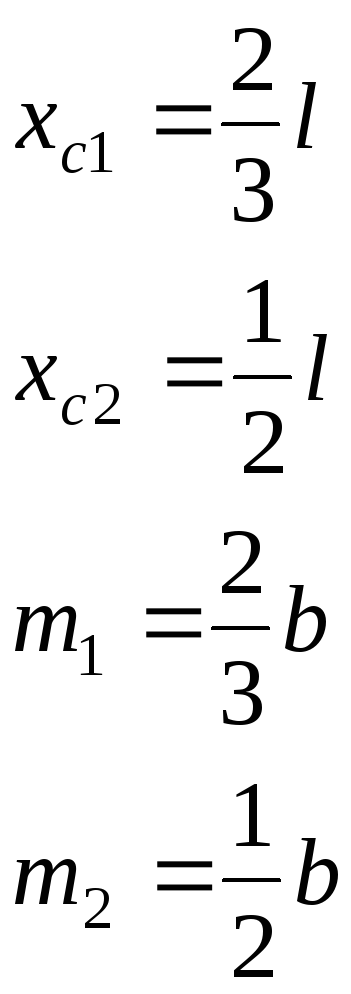4.2 Определение перемещений в стержневых системах методом Мора
Это универсальный метод, который заключается в использовании известной теоремы Мора о равенстве возможной работы внешних и внутренних сил и используется для определения линейных перемещений и углов поворота в любой стержневой системе от произвольной нагрузки. Метод широко применяется и при расчете статически неопределимых систем.
Пусть 1-е (грузовое) состояние представляет собой нагруженную стержневую систему заданной нагрузкой, а 2-е (единичное) состояние вызвано единичной нагрузкой Р = 1, действующей в направлении искомого перемещения. Тогда в соответствии с указанной выше теоремой получаем выражение, которое называют интегралом Мора (13)
где: искомое перемещение; Мр, Qp, Np внутренние усилия в стержневой системе, вызванные заданной внешней нагрузкой; М1, Q1, N1 внутренние усилия в стержневой системе, вызванные единичной нагрузкой, приложенной по направлению искомого перемещения в той точке (сечении), где определяется перемещение (при нахождении линейного перемещения прикладывается единичная сила Р = 1, при вычислении угла поворота прикладывается единичный момент m = 1); EI, EA, GA жесткости при изгибе, растяжении (сжатии) и сдвиге соответственно; поправочный коэффициент, учитывающий распределение касательных напряжений в поперечном сечении; l длина участка.
Суммирование производится по всем участкам стержневой конструкции.
При расчете балок средней и большой длины и рамных конструкций влиянием продольной и поперечной сил (вторым и третьим членами формулы (4,1)) можно пренебречь в силу их малого влияния на деформации изгиба. В этом случае интеграл Мора примет вид:
При расчете стержней, работающих только на растяжение (сжатие), и ферм в (4,1) останется только второй интеграл.
В конструкциях, испытывающих значительные поперечные силы (например, в коротких балках), необходимо учитывать влияние поперечных сил.
Пример 4.2. Вычислить прогиб и угол поворота свободного конца консоли (т. В) (рис. 4.9) от действия распределенной нагрузки.
1. В данной задаче один участок. Запишем для него выражение изгибающего момента в грузовом состоянии (рис. 4.9, а):
2. Для вычисления прогиба свободного конца (т. В) прикладываем в этой точке единичную силу Р = 1, т. е. создаем 1-е единичное состояние (рис. 4.9, б) и записываем выражение для единичного момента
3. Записываем и вычисляем интеграл Мора, используя выражение (4.2):
Знак «+» у говорит о том, что перемещение происходит по направлению единичной силы Р=1.
4. Для вычисления угла поворота прикладываем в заданном сечении (т. В) единичный момент (рис. 4.9, в) и записываем выражение для единичного момента М2 на данном участке:
5. Вычисляем интеграл Мора при 2-м единичном нагружении:
Знак «минус» говорит о том, что перемещение (поворот сечения С) происходит против направления единичного момента m = 1, т. е. по часовой стрелке.
Пример 4.3. Определить вертикальное перемещение 3 узла фермы от заданной нагрузки (рис. 4.10). Жесткость стержней ЕА = const.
Для определения перемещений в данной стержневой системе необходимо воспользоваться формулой Мора в виде:
1. Определяем усилия в стержнях фермы Np от заданной нагрузки. (рис. 4.10,а). Вначале определим реакции. В силу симметрии:
RA = RB = 1.5 P= 9 кН.
Вырезая узел 1 и узел 5 можно увидеть, что
N12 = N56 = — 1.5 P = — 9 кН,
N13 = N35 = 0.
Вырезая узел 4 получим N34 = P.
Далее, вырежем узел 2 (рис. 5.3). (sincos
— P – N12 – N23sin = 0.
N24 + N23cos = 0. N24 = — 5∙0.8 = — 4 кН.
В силу симметрии N36 = N23 = 5 кН, N46 = N24 = — 4 кН.
2. Определяем усилия в стержнях фермы от единичной нагрузки, действующей в направлении искомого перемещения (рис 4.10,б). Определяем реакции.
RA = RB = 0.5 P= 0,5.
Вырезая узел 1 и узел 5 получим
N12 = N56 = 0,5, N13 = N35 = 0.
Вырезая узел 4 получим N34 = 0.
Рассмотрим равновесие узла 2 (рис. 5.4).
y = 0, – N12 – N23sin = 0.
, x = 0, N24 + N23cos = 0.
В силу симметрии N36 = N23 = 5 кН, N46 = N24 = — 4 кН.
Для вычисления по формуле (4.3) удобно полученные значения усилий свести в таблицу.
Источник
2. Правило Мора-Верещагина (графический способ вычисления интеграла Мора)
Кроме метода начальных параметров существует эффективный универсальный метод определения перемещений в балках, рамах и упругих конструкциях произвольной конфигурации – метод Мора. Упругое перемещение 
(либо прогиб
, либо угол поворота сечения
) определяется по формуле:
, (1.3)
где 
– изгибающий момент от заданной нагрузки;
– изгибающий момент от единичной силы, приложенной в той точке, в которой определяется перемещение.
Упрощение операций интегрирования возможно для конструкций с прямолинейной осью постоянной жесткости и основано на том, что эпюры от единичных усилий на прямолинейных участках оказываются линейными. Рассматривая эту процедуру применительно к участку балки, преобразуем интеграл Мора с учетом этой особенности. На рис. 1.3 сверху показан участок балки с эпюрой 
общего вида, а внизу эпюра 
, представляющая собой линейную функцию. В результате несложного расчета (подробности смотри в учебнике) установлено, что интеграл произведения двух функций 
и 
численно равен площади эпюры 
, умноженной на величину момента, взятого с эпюры 
в сечении, соответствующем центру тяжести эпюры 
.
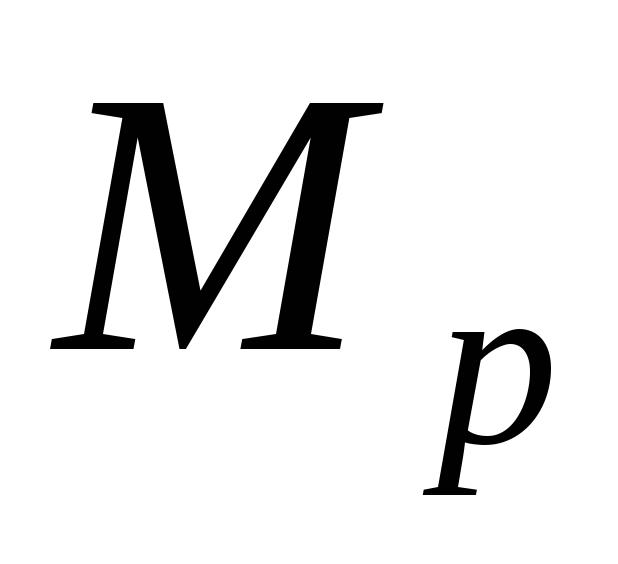
. (1.4)
Если балка имеет несколько участков по длине, формула Верещагина будет иметь вид
, (1.5)
где 
– площадь эпюры моментов от внешней нагрузки (грузовой эпюры); 
– ордината единичной эпюры под центром тяжести грузовой эпюры; 
– число участков по длине балки.
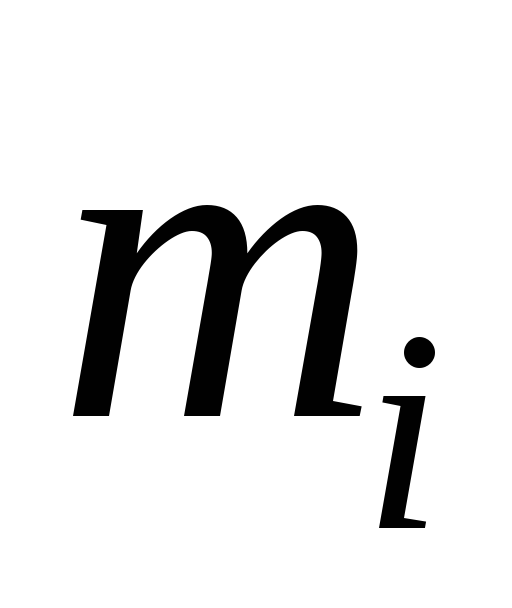
При пользовании этой формулой надо уметь вычислять площади и координаты центров тяжести основных фигур: прямоугольника, прямолинейного треугольника и криволинейного треугольника. Минимально необходимые справочные данные приведены в табл. 1.1. Процедуру графического вычисления называют «перемножением» эпюр.
Эпюры 
и
эпюры ,
тяжести
Эпюры 
и
эпюры ,
тяжести
Примечания: 1. Все кривые в табл. 1.1 – квадратные параболы. 2. При «перемножении» эпюр одного знака их произведение положительно. 3. При «перемножении» эпюр разных знаков их произведение отрицательно.
В случае, если эпюра тоже линейная, операция перемножения обладает свойством коммутативности: безразлично, умножается ли площадь грузовой эпюры на ординату единичной или площадь единичной на ординату грузовой.
Рассмотрим на примере расчетной схемы, показанной на рис. 1.4, порядок решения задач при определении перемещения с помощью правила Мора-Верещагина. Определим прогиб в точке .
Чтобы построить эпюры 
и 
,можно не определять опорные реакции: достаточно сосчитать момент на опоре
от нагрузки на консоли, построить эпюру на консоли, а затем соединить прямой линией значениеM на опореB с нулем на опореA.
В соответствии с формулой (1.5)
.
Источник