Параметры модели кулона мора

Расчеты грунтов по модели Кулона-Мора

В качестве критерия прочности для оползней скольжения (как в скальных так и в дисперсных грунтах) наиболее часто используется зависимость Мора-Кулона:

где τ — прочность на сдвиг; u – поровое давление; σ – эффективное нормальные напряжения; φ’ – эффективный угол внутреннего трения; с – сцепление.

Графическое представление зависимости Мора-Кулона приведено на рис. 1.

Рис. 1. Графическое представление зависимости Мора-Кулона

Условие Мора-кулона может быть использовано как в полных, так и в эффективных напряжениях. В терминах полных напряжений, критерий Мора-кулона приобретает следующую простую форму:

где t — прочность на сдвиг; s – полное нормальные напряжения; j – угол внутреннего трения; с – сцепление.

Необходимыми свойствами грунтов для расчета устойчивости склона на основе критерия прочности Мора-Кулона являются сцепление и угол внутреннего трения. Они не используются в решении, при расчете напряжений и деформаций, но необходимы для расчета зон пластического течения, в которых значения напряжений превысили критические значения и закон Гука не выполняется. Использование критерия прочности Мора-Кулона позволяет сравнить расчетное напряжение при сдвиге с теоретическими предельными значениями напряжений.

Однако, при решении практических задач, перечень необходимых свойств грунтов для оценки устойчивости склонов, существенно расширяется. В зависимости от постановки задачи в полных или эффективных напряжениях, определение прочностных характеристик грунта должно выполняться по недренируемой схеме, или по схеме консолидируемых дренированных испытаний. При оценки устойчивости оползневых склонов (в условиях протекания оползневого процесса) в зоне скольжения должны использоваться остаточные параметры прочности грунтов, при оценке потенциальной оползневой опасности склона (в случае отсутствия оползневого процесса на исследуемом склоне) – должны использоваться пиковые параметры прочности грунтов.

В свою очередь, удельное сцепление грунтов может быть представлено как сумма двух параметров — сс- структурного сцепления и Σw – связанности грунта при заданной влажности.

По Н.Н. Маслову выделяются три типа глинистых грунтов: жёсткие (хрупко-упругие); скрытопластичные (вязкопластичные) и пластичные (вязкотекучие).

К жёстким глинистым грунтам в большинстве случаев относятся грунты до четвертичного возраста. Связанность жестких глинистых грунтов много меньше их структурного сцепления и может быть приравненной к 0, а угол внутреннего трения мало зависит от влажности. Уравнение сопротивления сдвигу для таких грунтов имеет следующий вид:

Прочность на сдвиг скрыто пластичных глинистых грунтов выражается зависимостью:

При этом величины φ_w и S_w сильно зависят от влажности. В случае нарушения структуры скрытопластичных глинистых грунтов зависимость прочности на сдвиг принимает следующий вид:

Прочность на сдвиг идеально пластичных глинистых грунтов выражается зависимостью:

Как следует из приведенной формулы, в таких грунтах угол внутреннего трения и структурное сцепление принимаются равными 0. В случае нарушения структуры пластичных глинистых грунтов сопротивление прочности на сдвиг в них меняется очень слабо по сравнению с ненарушенной структурой.

В настоящее время существует большое количество модификаций классической зависимости Мора-Кулона. Типичным примером является билинейная модель прочности.

На рис. 1 представлен модифицированный билинейный критерий Мора-Кулона. Огибающая кривая прочности определяется двумя значениями σ (угла внутреннего трения) и удельного сцепления, а также нормальным напряжением в плоскости сдвига, при котором наступает состояние текучести.

Рис. 1. Билинейная модель огибающей кривой сдвига.

Согласно данной модели, в том случае, если нормальное напряжение в плоскости сдвига больше заданного значения, в критерии прочности Мора-Кулона используются значения угла внутреннего трения и сцепления Phi2 и С(computed) соответственно. Билинейная модель прочности была первой попыткой учесть нелинейность в критерии Мора-Кулона.

Типичным примером билинейной модели прочности Мора-Кулона является критерий Паттона (Patton FD (1966). Multiple modes of shear failure in rock. Proceedings of 1st Congress of International Society of Rock Mechanics, Lisbon, 1, 509–513.), разработанный для скальных грунтов и учитывающий эффект шероховатости трещин:

Где φ_b – базовый угол внутреннего трения породы, i – угол шероховатости, σ_n – эффективное напряжение, σ_ny — эффективное нормальное напряжение, вызывающее проскальзывание микродефектов шероховатости, с_jed – эквивалентное сцепление (прочность на сдвиг за счет зацепления микродефектов).

Данная разновидность модели прочности Мора-Кулона, в последние годы так же нашла широкое применение при оценке устойчивости различных нестационарных состояний оползневых (потенциально оползнеопасных) склонов, таких как падение Ку при быстрой сработке уровня подземных вод или при по этапном псевдостатическом анализе учета сейсмического воздействия (Дункан и Райт).

Модель Кулона-Мора пожалуй самая распространенная модель используемая в геотехнических расчетах. С момента создания данной функции прошло уже несколько столетий, при этом модель не только не потеряла своей актуальности, но и постоянно используется в создании новых аналитических выражений. В инженерно-строительной практике данная модель внедренна в различные методики. С ее помощью рассчитывают основания и фундаменты по двум предельным состояниям.

Источник

Выбор модели грунта и её параметров в расчётах геотехнических объектов

АННОТАЦИЯ: Статья посвящена вопросу обоснования выбора математической модели грунта и определению ее параметров. В качестве сопоставляемых моделей выбраны две наиболее популярные упругопластические модели: модель Кулона-Мора и модель упрочняющегося грунта. Приведены результаты методики определения расчетных параметров этих моделей путем сопоставления результатов компьютерного моделирования стабилометрических испытаний в программе PLAXIS с лабораторными данными. В рамках выбранных моделей выполнены расчеты напряженно-деформированного состояния грунтовых массивов с ограждающими конструкциями. Дан анализ выявленных характерных различий в прогнозе деформаций объектов и усилий в конструкционных элементах.

Комплексное расчетное обоснование проектов строительства, эксплуатации, реконструкции сооружений в сложных инженерно-геологических условиях, в том числе в стесненной городской застройке, стало невозможным без использования современных компьютерных программ. При этом следует помнить, что расчеты, по результатам которых будет принято проектное решение, следует проводить только после серии предварительных расчетов исследовательского характера, учитывающих влияние ряда факторов при математическом моделировании работы геотехнической системы. Наиболее важными из них являются вопросы создания геометрической модели, конечно-элементной расчетной схемы и выбора модели грунта.

В современной практике геотехнических расчетов используются математические модели грунта разной степени сложности. Преимущество простых моделей заключается в меньшем количестве входных параметров, а также в простоте и ясности определяющих уравнений. Однако результаты моделирования в этом случае могут быть достаточно грубыми и плохо согласующимися с реальными данными. Сложные, усовершенствованные модели позволяют

описать поведение грунта более точно, но они требуют более широкого набора характеристик грунта, а также достаточной осведомленности и опытности инженера при выборе модели, ее параметров и анализе полученных результатов расчетов.

2. Две альтернативные модели

Декларируемый в строительных нормах принцип проектирования по предельным допускаемым деформациям может быть реализован в полной мере только при использовании упругопластических моделей грунта, позволяющих описывать напряженно-деформированное состояние на всем диапазоне изменения нагрузок, вплоть до предельных (разрушающих) значений. Возьмем две такие модели: упругоидеальнопластическую модель (модель Кулона-Мора) (Бугров, 1974) и упругопластическую модель с упрочнением (Schanz et al, 1999). Эти модели включены в программный комплекс PLAXIS, что позволяет провести сравнительный анализ и оценить влияние выбранной модели и ее расчетных параметров на прогнозируемое развитие напряженно-деформированного состояния грунта.

При расчетном обосновании многих геотехнических проектов с помощью PLAXIS инженеры часто отдают предпочтение наиболее простой из этих моделей — модели Кулона-Мора (КМ), порой из-за ограниченных данных инженерно-геологических изысканий. Эта модель требует определения всего четырех расчетных параметров грунта: модуля общей деформации Е, коэффициента Пуассона ν, сцепления с и угла трения φ. Модель упрочняющегося грунта (УГ) является усовершенствованной упругопластической моделью, для которой, помимо параметров прочности с и φ, требуется определить модули деформации при первичном нагружении Е и разгрузке Е_ur, одометрический модуль Е_oed, а также показатель степени зависимости жесткости грунта от уровня напряжений m. Эти входные расчетные характеристики жесткости соответствуют определенным эталонным напряжениям, при которых выполнены испытания грунта в стабилометре и одометре. Реальные же характеристики жесткости рассчитываются программой PLAXIS по достигнутым значениям напряжений с учетом развития напряженно-деформированного состояния грунта по гиперболической зависимости.

3. Определение параметров моделей. Лабораторные и виртуальные испытания грунта

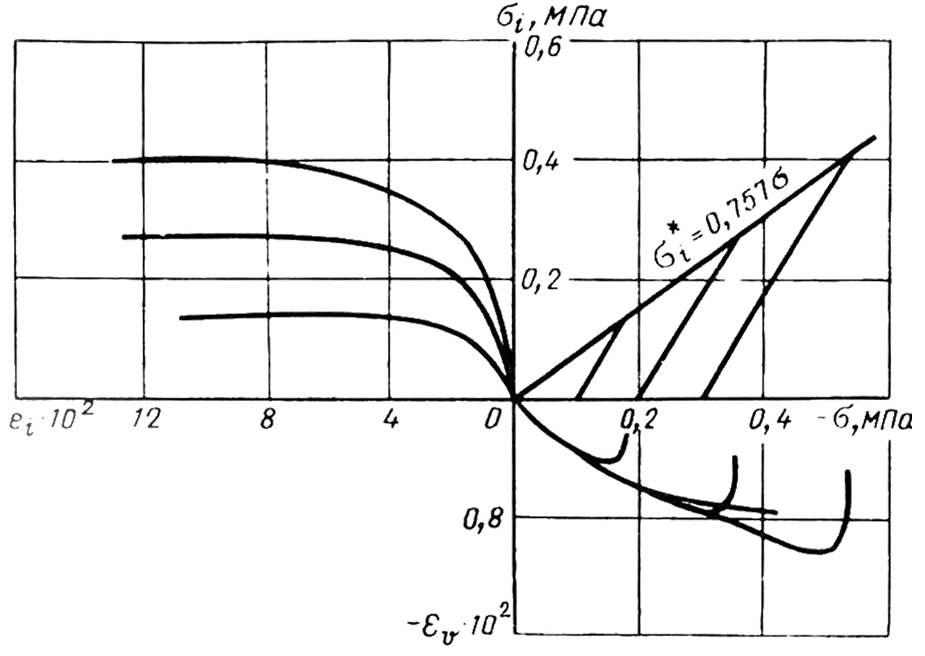
Выбор расчетной модели грунта и определение ее параметров возможны на основе сопоставления результатов лабораторных испытаний и их виртуальных компьютерных аналогов. На рис. 1 представлены результаты стабилометрических испытаний песка в виде графического паспорта грунта (Зарецкий, 1988). По этим данным, согласно методике определения расчетных характеристик (Brinkgreve et al, 2008), были получены деформационные и прочностные параметры модели КМ и модели УГ (таблица 1). В качестве базовой характеристики жесткости принимается секущий модуль деформации Е₅₀ ref , соответствующий значению бокового давления в стабилометре р ref =100 кПа и 50% прочности грунта.

Программа PLAXIS располагает опцией оперативного математического моделирования стандартных лабораторных испытаний грунтов с использованием имеющихся расчетных моделей (опция «soil test»).

Рис. 1. Графический паспорт песка

Таблица 1. Расчетные параметры моделей грунта

Источник

Модифицированная модель Мора-Кулона

Модифицированная модель Мора-Кулона характеризуется линейно-упругим идеально-пластическим поведением. Соответствующее соотношение напряжение-деформация показано на следующем рисунке.

А. Обратимые упругие напряженные состояния

Модель демонстрирует упругое поведение в диапазоне допустимых напряжений, ограниченном граничным условием. В пределах этой области, поверхности текучести, существует изотропная линейно-упругая зависимость напряжение-деформация по закону КРЮКА ‘.

при Жёсткость

Пропорциональная связь линейно-упругого поведения описывается постоянным модулем упругости.

C. Необратимые пластические состояния растяжения

Если напряжение соответствует граничному условию и находится на поверхности текучести, поведение меняется на пластическое, которое определяется правилом текучести. По мнению Мора-Кулона, это приводит к следующему:

Результирующая поверхность текучести показана на следующем рисунке в трехмерном пространстве главных напряжений.

Терория разрушения напряжения

Критерий разрушения Мора-Кулона предполагает, что материал разрушится, если внутреннее сопротивление сдвигу ниже, чем напряжения сдвига, возникающие в результате внешних нагрузок.

Входные параметры

Для определения материала с помощью модифицированной модели Мора-Кулона требуется пять входных параметров.

• Модуль упругости E
• Коэффициент Пуассона (коэффициент Пуассона) ν
• Сплоченность c
• Угол трения φ
• Угол дилатанса ψ

Пригодность

Модель Мора-Кулона можно рассматривать как грубое приближение фактического поведения грунта, поскольку предполагается линейно-упругое поведение и модуль упругости постоянным.

Это позволяет с минимальными усилиями определить свойства материала. Модель условно пригодна для расчета деформаций. Рекомендуется аппроксимировать увеличение жесткости грунта с глубиной путем моделирования нескольких подслоев, с постоянной жесткостью, но увеличивающейся в некоторых слоях с глубиной.

Модель материала с критерием разрушения Мора-Кулона в принципе пригодна для расчета устойчивости.

Источник