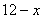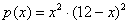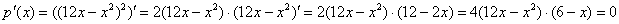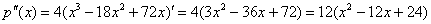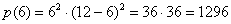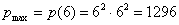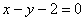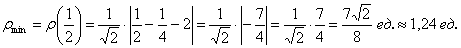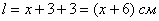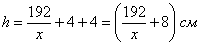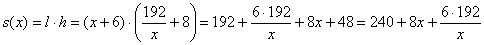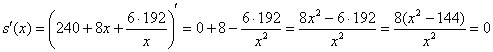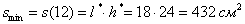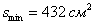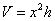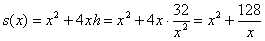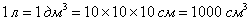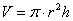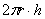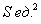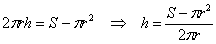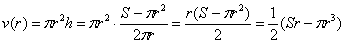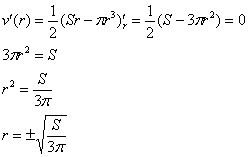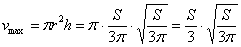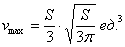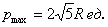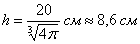Определить размеры прямоугольного бассейна имеющего наименьшую поверхность при условии

Экстремальные задачи с производной

Совершенно верно, иногда от таких задач действительно захватывает дух. Сегодня на уроке мы разберём ещё одно важное приложение производной, имеющее самое что ни на есть прикладное значение! Речь пойдёт о задачах с конкретным геометрическим, физическим, экономическим и т.д. содержанием, в которых исходя из условия, нужно самостоятельно составить функцию и найти её точку минимума либо максимума (и/или, соответственно, минимум либо максимум).

Для полноценного изучения урока необходимо уметь находить производные, ПОНИМАТЬ, что такое производная и быть знакомым с понятиями возрастания, убывания и экстремума функции. Таким образом, начинающим рекомендую начать с вышеуказанных статей, чтобы не словить здесь реальный экстрим =) А уже заматеревшие студенты не должны испытать особых трудностей. Разминочная алгебраическая задача и новый материал по ходу решения:

Известно, что сумма двух положительных чисел равна 12. Какими должны быть эти числа, чтобы произведение их квадратов было максимальным?

Решение: прежде всего, хорошо осознаем, что от нас требуется: в условии фигурируют два положительных числа, причём ни то, ни другое мы не знаем. Но вот их сумма равна 12.

Если это, например, 2 и 10, то произведение квадратов ;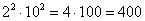
если 7 и 5, то 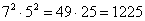и т.д.

И нам нужно отыскать такую пару, для которой данное произведение будет наибольшим. Понятно, что с методом подбора тут замучаешься, к тому же искомые числа ведь могут оказаться и дробными. Поэтому привлечём на помощь могучий аппарат математического анализа.

Но сначала вспомним школу и вспомним, как, наивно хлопая ресницами, мы что-то обозначали за «икс»…. Обозначим за 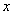одно из чисел. Тогда второе число будет равно:

Проверим, что их сумма действительно равна 12:
– а ведь и правду говорят, что всё гениальное просто =)

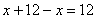
Теперь составим функцию произведения их квадратов:

Многие читатели уже понимают последующие шаги: далее нужно найти производную, критические точки и обнаружить точку (и), в которой функция 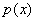достигает максимума (если таковые, конечно, вообще существуют).

И небольшой вопрос техники: производную здесь можно найти несколькими способами. На мой взгляд, удобен следующий вариант: загоняем множители под единую степень и раскрываем там скобки: 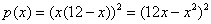, после чего дифференцируем сложную функцию:

Итак, 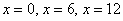– критические точки.

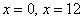
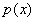
По условию оба числа положительны, поэтому значения сразу исключаем из рассмотрения. Осталось проверить достаточное условие экстремума для точки и выяснить, достигает ли там функция минимума либо максимума. А может статься, и ничего не достигает.

Проверка вам хорошо знакома: чертим числовую ось, выясняем знаки производной слева и справа от точки 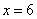и выносим вердикт. Так решать можно, и это будет правильным решением, но есть и другой путь!

Второе достаточное условие экстремума

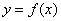
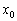
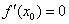
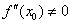
Пусть производная функции равна нулю в критической точке :
и пусть там существует вторая ненулевая производная: . Тогда:

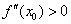
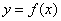
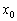
если , то функция достигает минимума в точке ;
если 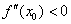, то – максимума.

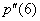
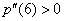
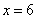
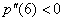
В нашем случае нужно найти вторую производную и вычислить – если окажется, что , то является точкой минимума; если же – то точкой максимума.

Для удобства дифференцирования утрамбуем предшественницу:
и незамедлительно оценим это удобство:

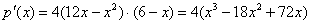
Подставим критическое значение :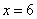
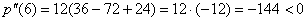
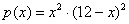
, значит, функция достигает максимума в данной точке:

Ответ: искомые числа: 6 и 6, при этом максимальное произведение квадратов:

Вообще говоря, по условию не требовалось находить само произведение, но по правилам хорошо тона его лучше рассчитать и указать в ответе. К тому же это весьма любопытно.

На практике в подавляющем большинстве случаев встречаются задачи с геометрическим смыслом, и поэтому основная часть урока будет посвящена именно им. Начнём с несложного типового примера, который почему-то довольно часто вызывает проблемы:

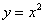
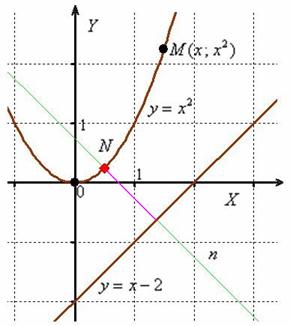
Найти наименьшее расстояние между параболой и прямой

Решение: вот, пожалуйста, самый что ни на есть практический смысл – представьте, что вам нужно пройти от дороги к дороге. Совершенно понятно, что в отсутствии препятствий это наиболее выгодно осуществить по кратчайшему пути.

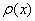
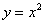
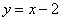
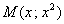
Поскольку условие запрашивает наименьшее расстояние, то, очевидно, нам нужно составить функцию расстояния между параболой и прямой . За аргумент этой функции принимаем абсциссу точки , которая принадлежит параболе и «свободно перемещается по ней»:

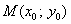
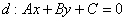
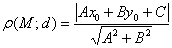
Используем формулу расстояния от точки до прямой :

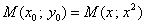
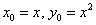
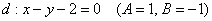
В нашем случае (т.е. );
.

Таким образом:
– функция расстояния между параболой и прямой, зависящая от абсциссы точки параболы.

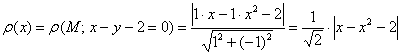
Дифференцируем по обычным правилам, невзирая на модуль: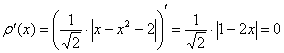

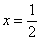
– критическая точка

Проверим выполнение достаточного условия экстремума. Оцените, насколько второе достаточное условие приятнее и удобнее 1-го:
для всех «икс». В частности:
, следовательно, функция достигает минимума в точке :

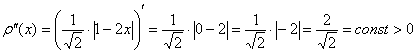
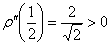
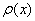
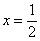
Искомая «дорога» изображена малиновым отрезком на чертеже.

Ответ:

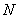
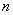
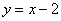
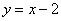
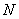
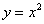
Физики в лирике могут найти ординату точки , уравнение нормали и её точку пересечения с прямой . Кстати, почему кратчайший путь проходит именно по нормали? Приложите ребро ладони к прямой и начните плавно сдвигать его к параболе: первая точка, которой вы коснётесь – будет в точности точка , ваша рука займёт положение касательной к графику функции в данной точке, а расстояние между двумя прямыми как раз и определится малиновым отрезком нормальной прямой.

Следующая задача для самостоятельного решения:

Из куска проволоки длиной 30 см требуется согнуть прямоугольник наибольшей площади. Каковы размеры этого прямоугольника?

Давайте немного проанализируем условие:

Что требуется найти? Очевидно, длину и ширину – это «традиционные» характеристики, определяющие прямоугольник.

Какую функцию нужно составить? Наверное, многие уже поняли данную закономерность:

Требуется найти минимальную/максимальную площадь? Составляем функцию площади;
Минимальную/максимальную диагональ? Составляем функцию длины диагонали;
Минимальный/максимальный периметр? Составляем функцию периметра
и т.д.

Напоминаю, что периметр – это длина границы фигуры, в данном случае – сумма длин сторон прямоугольника. Кстати, задачу легко переформулировать «чисто математически»:

«Найти прямоугольник максимальной площади, если его периметр равен 30 см»

Выполните схематический чертёж, подумайте, что обозначить за «икс» (впрочем, чего тут думать), составьте функцию площади 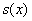– и дальше по накатанной.

Краткое решение и ответ в конце урока.

После простых разогревающих заданий рассмотрим что-нибудь поосновательнее:

На странице книги печатный текст должен занимать (вместе с промежутками между строк) 192 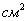. Верхнее и нижнее поля занимают по 4 см, левое и правое – по 3 см. Если принимать во внимание только экономию бумаги, то каковы должны быть наиболее выгодные размеры страницы?

Решение: разруливаем задачу по той же логической схеме:

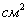
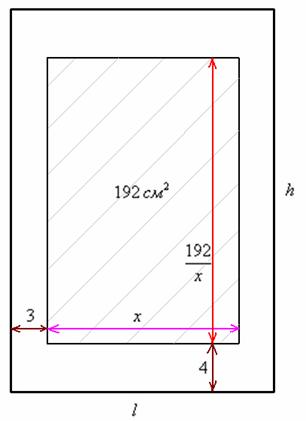
Что требуется найти? Наиболее выгодные размеры страницы. А страница обычно имеет форму прямоугольника. Коль скоро речь идёт об экономии бумаги, то, очевидно, нужно найти такую ширину и высоту листа, чтобы его площадь была минимальна. Из чего следует, что нам необходимо составить функцию площади страницы. Причём условие жёстко задаёт размеры полей, а вот под область печати отведено 192 и её размеры могут быть произвольными (заштрихованный прямоугольник на схематическом чертеже):

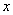
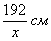
Обозначим за ширину области печати (малиновый отрезок) (можно обозначить высоту – получится равноценное решение). Тогда высота области печати:
(красный отрезок).

Учитывая известные значения полей, найдём ширину всего листа:

И его высоту:

Составим функцию площади листа и сразу подготовим её для дифференцирования:

Найдём критические точки:

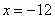
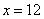
Точка не удовлетворяет геометрическому смыслу задачи, а вот значение куда более интересно.

Проверим выполнение достаточного условия экстремума: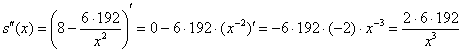

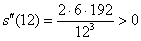
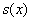
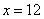
(считать тут совсем не обязательно), значит, функция достигает минимума в точке .

Таким образом, размеры оптимального листа: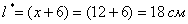
;
;
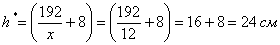
при этом минимальная площадь:

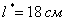
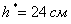
Ответ: ширина оптимальной страницы: , её высота: ; при этом минимальная площадь:

Как видите, основная трудность состоит в том, чтобы разобраться в условии и составить нужную функцию. И в преодолении этой трудности здОрово помогает чертёж. Поэтому всегда стараемся выполнить схематический чертёж или хотя бы рисунок. Даже в таких простых случаях, как в Задаче №3, не говоря уже о только что разобранном примере.

Следующее задание для самостоятельного решения:

В полукруг радиуса 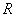вписать прямоугольник наибольшего периметра

Просто и со вкусом. И снова несколько подсказок, которые полезно иметь в виду и при решении других задач:

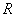
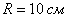
! Во-первых, обратите внимание, что условие сформулировано в общем виде и величина считается известной. Если совсем тяжко, решите задачу с каким-нибудь конкретным значением радиуса, например, с радиусом .

! Во-вторых, выполните схематический чертёж, который здесь очень прост: одна из сторон прямоугольника лежит на диаметре полукруга, а вершины противоположной стороны – на полуокружности. Очевидно, что в полукруг можно вписать бесконечно много прямоугольников и ваша задача найти такой, периметр которого максимален. Какую функцию нужно составлять, надеюсь, всем понятно. Подумайте, что удобнее обозначить за «икс» и, кроме того, освежите в памяти теорему Пифагора.

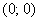
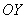
! В-третьих, задачу можно решить в разных стилях. Образец решения оформлен «исключительно геометрически», однако есть и такой вариант: начертить полукруг в декартовой системе координат – в верхней полуплоскости центром в точке . Далее составить уравнение окружности, выразить функцию верхней полуокружности и рассмотреть переменные координаты вершины прямоугольника, которая на этой полуокружности лежит. Более того, ввиду симметрии фигур относительно оси задачу можно решить в 1-й координатной четверти, т.е. изобразить лишь четвертинку круга (но затем не забыть удвоить одну из сторон прямоугольника). Кому как удобнее.

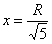
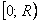
! И, в-четвёртых, эта задача о том, что иногда совсем не обязательно «разбивать лоб» о новый материал 😉 Если вам показался слишком сложным 2-й достаточный признак экстремума, то никто ведь не запрещает использовать 1-й достаточный признак – определите знаки первой производной слева и справа от критической точки на промежутке и сделайте вывод.

Наш урок в самом разгаре и настало время разобрать задачи, которые встречались в моей практике без преувеличения десятки раз:

Определите размеры открытого бассейна объемом 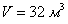, имеющего форму прямоугольного параллелепипеда с квадратным дном, на облицовку стен и дна которого уйдет наименьшее количество материала.

Решение: представили бассейн. Квадратное дно. Стены. Размеры бассейна однозначно определяются его длиной и шириной, которые в данном случае совпадают (по условию дно квадратное) и глубиной (высотой стенки). Требуется найти такие размеры бассейна, чтобы на облицовку его поверхности ушло наименьшее количество материала (например, плитки). Из чего следует, что нам нужно составить функцию суммарной площади дна и 4 стен. Изобразим на чертеже развёртку бассейна – его дно и 4 стенки, которые аккуратно лежат рядышком: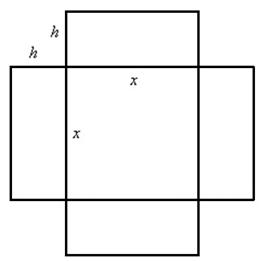

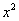
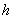
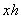
За «икс» здесь, конечно же, напрашивается обозначить сторону квадрата. Тогда площадь дна равна . Осталось выразить – высоту стены и найти её площадь .

По условию, объём бассейна равняется 32 кубическим метрам. Даже не вспоминая и не разыскивая соответствующую формулу, нетрудно сообразить, что объём прямоугольного параллелепипеда – это произведение площади его «дна» на высоту:

В нашем случае: .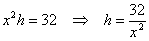

Составим функцию суммарной площади дна и четырёх одинаковых стен бассейна:

Найдем критические точки: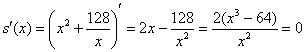

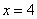
– критическая точка.

Проверим выполнение достаточного условия экстремума: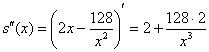

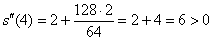
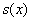
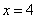
, значит, функция достигает минимума в точке .

Таким образом:
сторона оптимального бассейна ;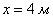
глубина ;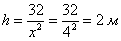
при этом минимальная площадь облицовки: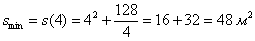
.

Ответ: сторона оптимального бассейна: 4 м, глубина: 2 м; при этом минимальная площадь облицовки .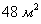

Кстати, это решение совсем не очевидно – так, например, на оптимальный вариант с успехом претендует «лягушатник» размером 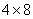глубиной 1 метр, и «на глазок» очень трудно определить, что выгоднее – ведь площадь облицовки последнего лишь ненамного больше: . И да – надо отдать должное авторам задач за реалистичность, а то не так уж и редко получаются забавные результаты а-ля бассейн глубиной 32 метра, что называется, купайтесь и не квакайте =)

Аналогичная задача про суровые челябинские шпроты:

Каковы должны быть размеры консервной банки цилиндрической формы, чтобы на её изготовление пошло наименьшее количество материала, если объем банки 0,5 литра?

Но перед тем как решать, пожалуйста, ознакомьтесь с парой полезных замечаний:

Во-первых, литр – это единица объёма. Я специально заострил внимание на физике, поскольку на обывательском уровне литр очень часто неверно отождествляют с килограммом (единицей массы). Ощутите разницу – пол-литровая банка кильки и та же банка, наполненная гвоздями. Один литр равен одному кубическому дециметру или тысяче кубических сантиметров:

А теперь очень важный момент: так как размеры банки, очевидно, выразятся в сантиметрах, то 0,5 литра следует сразу перевести в кубические сантиметры!

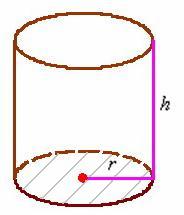
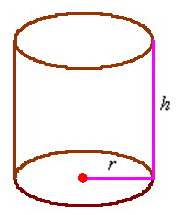
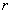
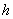
К слову, что это за размеры? Цилиндр стандартно определяется радиусом основания и высотой . Во-вторых. Освежим в памяти формулы:

площадь круга: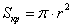
площадь боковой поверхности цилиндра: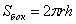
объём цилиндра:

И в который раз остановлюсь на важном принципе эффективного изучения математики: не зубрите формулы (без крайней необходимости, конечно). В частности, позабытую площадь боковой поверхности цилиндра несложно вывести даже в уме: представьте стенку консервной банки без дна и крышки. Сделайте вертикальный разрез и расправьте боковину на столе. 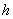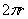В результате получился прямоугольник, одна из сторон которого, понятно, равна высоте банки , а другая – длине окружности . Площадь же прямоугольника рассчитывается элементарно:

Решение проводится по аналогии с Задачей 6, примерный образец в конце урока.

Закрепим типовик своего рода обратными задачами:

Определить наибольшую вместимость цилиндрического бака, если его площадь поверхности (без крышки) должна равняться

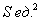
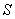
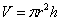
Решение: в данном случае всё наоборот – известна площадь поверхности (если трудно, замените конкретным числом) и требуется определить максимальный объём бака.

За «икс» обозначим… а зачем, собственно, лишние буквы? Ещё с первых уроков о производной многие поняли, что дифференцировать можно по любой переменной, и сейчас мы окончательно избавимся ото всех комплексов.

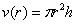
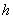
От какой переменной искать функцию объёма? В соответствующей формуле наиболее «наворочен» радиус, поэтому логично попытаться составить функцию , зависящую именно от него. Нужно только выразить высоту .

Сумма площадей дна (не забываем, что крышка отсутствует!) и боковой поверхности в точности равна известному значению: 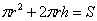, откуда находим:

Таким образом:

Найдём критические точки:

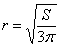
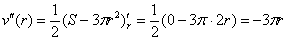
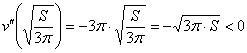
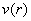
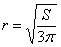
Геометрическому смыслу задачи, разумеется, удовлетворяет положительный корень . Проверим выполнение достаточного условия экстремума:

, значит, функция достигает максимума в точке .

При этом высота бака: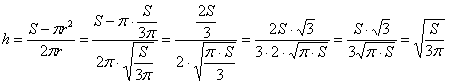

максимальный объём:

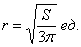
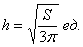
Ответ: радиус основания оптимального бака: , высота: , при этом максимальный объём:

Решение в общем виде, бывает, кажется непривычным, однако оцените его универсальность – теперь достаточно лишь подставить конкретное значение площади и сразу рассчитать размеры оптимального цилиндра.

Успокоительное задание для самостоятельного решения:

Прямоугольный лист картона имеет размеры 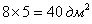. Требуется вырезать по его углам такие квадраты, чтобы после загибания оставшихся кромок получилась коробка наибольшей вместимости.

Краткое решение и ответ в конце урока.

Помимо рассмотренных выше геометрических объектов, на практике также можно встретить треугольники, трапеции, шары, конусы и т.д., но это более редкие гости (что касаемо забытых формул – справочники в помощь). К сожалению, нельзя объять необяътное, и поэтому в рамках этой статьи я ограничился самыми распространёнными примерами. И действительно, задач ведь придумать можно очень много – и всех их не перерешаешь, главное, чтобы вы хорошо поняли принципы и методы решения, которые я постарался изложить максимально пОлно и качественно.

Кроме того, существуют экстремальные задачи физического, химического, экономического и др. содержания, однако по причине отсутствия таковых в моей коллекции кот даже и не плакал. Но, понимая, что такое производная и обладая элементарной техникой дифференцирования, вы не должны испытать серьёзных затруднений с этими задачами, хотя для их решения, конечно, нужно разобраться и в самой физике/химии/экономике или иной предметной области.

Решения и ответы:

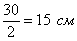
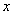
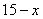
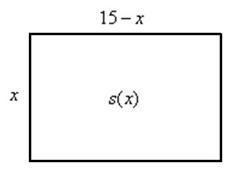
Пример 3: Решение: найдем полупериметр прямоугольника: . Обозначим через длину стороны прямоугольника (любую). Тогда – длина смежной стороны:

Составим функцию площади прямоугольника: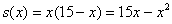
.
Найдем критические точки: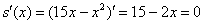

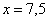
– критическая точка.
Проверим выполнение достаточного условия экстремума.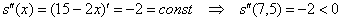
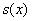
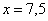
, значит, функция достигает максимума в точке .
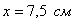
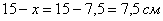
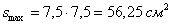
Таким образом – оптимальная длина стороны прямоугольника, длина смежной стороны: ; при этом максимальная площадь:

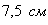
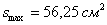
Ответ: оптимальный прямоугольник представляет собой квадрат со стороной ; при этом максимальная площадь: .

Пример 5: Решение: выполним чертёж: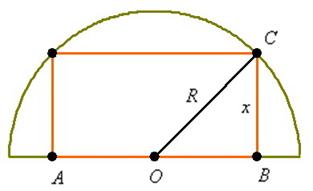

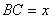
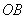
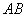
Пусть (как вариант, за «икс» можно обозначить или даже ).
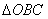
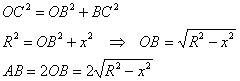
Рассмотрим прямоугольный . По теореме Пифагора:

Составим функцию периметра прямоугольника: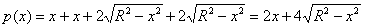

Найдём критические точки: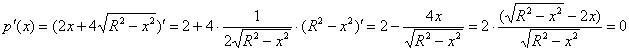
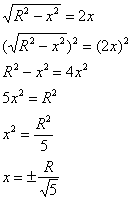
Решим простейшее иррациональное уравнение:

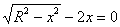
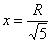
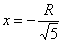
Уравнению удовлетворяет корень (корень же появился в результате возведения обеих частей в квадрат и является посторонним).
Проверим выполнение достаточного условия экстремума.
Способ первый: определим знаки производной: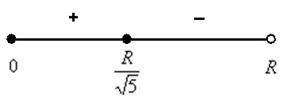

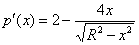
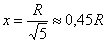
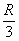
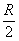
Примечание: используем стандартный метод интервалов: в производную подставляем какое-нибудь значение, лежащее левее точки , например, и подставляем какое-нибудь значение из правого интервала – проще всего взять .
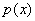
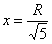
Вывод: функция достигает максимума в точке .
Способ второй: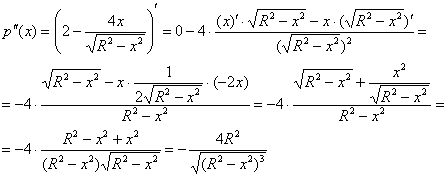

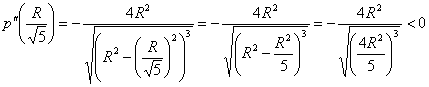
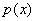
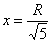
, значит, функция достигает максимума в точке .
Таким образом, размеры оптимального прямоугольника: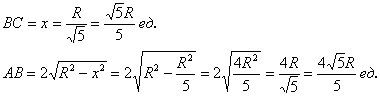

При этом максимальный периметр: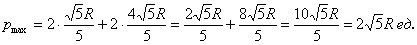

Ответ: оптимальный прямоугольник имеет размеры 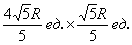, при этом максимальный периметр:

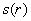
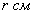
Пример 7: Решение: составим функцию площади полной поверхности цилиндра , зависящую от его радиуса. Пусть – радиус дна (и крышки) консервной банки:

Тогда площадь дна: 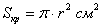. Столько же и площадь крышки.
По условию объём консервной банки равен :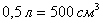

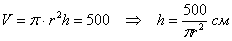
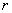
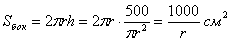
Выразим через площадь боковой поверхности банки:

Площадь полной поверхности банки равна сумме площадей дна, крышки и боковой поверхности: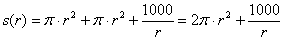

Найдём критические точки: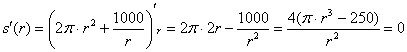

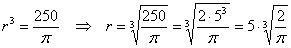
– критическая точка.
Проверим выполнение достаточного условия экстремума: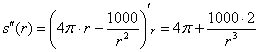

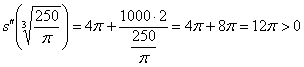
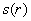
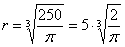
, значит, функция достигает минимума в точке .
Высота оптимальной банки: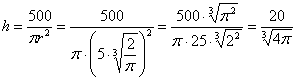

Ответ: радиус основания оптимальной банки: 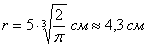, её высота:

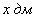
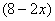
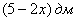
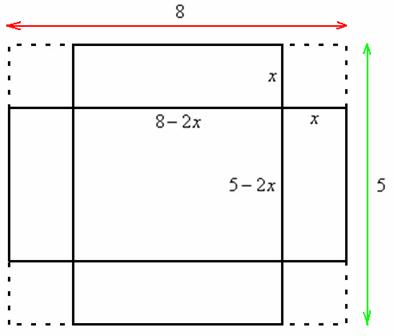
Пример 9: Решение: пусть – сторона вырезаемых по углам квадратов (высота будущей коробки). Тогда смежные стороны дна коробки составят и :

Составим функцию объёма коробки: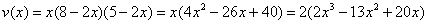

Найдём критические точки: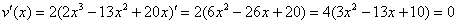

Решим квадратное уравнение: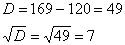

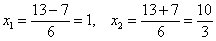
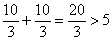
– критические точки. Второе значение не удовлетворяет геометрическому смыслу задачи, поскольку суммарная длина отреза сверху и снизу (ширины листа).
Проверим выполнение достаточного условия экстремума: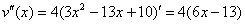

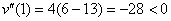
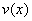
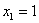
, значит, функция достигает максимума в точке .
Ответ: размеры оптимальной коробки:
– высота (сторона вырезаемых по углам квадратов);
– длина;
– ширина;
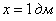
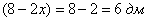
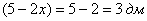
при этом максимальный объем: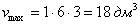
.

Автор: Емелин Александр

(Переход на главную страницу)

«Всё сдал!» — онлайн-сервис помощи студентам

Источник