Основанием открытого бассейна является квадрат
Помощь в написании контрольных, курсовых и дипломных работ здесь.
Определить глубину открытого бассейна
Определить глубину открытого бассейна с квадратным дном и объемом 500 м так, чтобы на половину его.
основанием пирамиды яв-ся квадрат со стороной 6см
основанием пирамиды МАВСD яв-ся квадрат со стороной 6см.Ребро МВ перпендикулярно плоскости.
Основанием четырехугольной пирамиды является параллелограмм
Основанием четырехугольной пирамиды MABCD является параллелограмм ABCD. F – середина ребра MB, K –.

Вычислите объем призмы, основанием которой является прямоугольник (все измерения вводить с.
Записывайтесь на профессиональные IT-курсы здесь
объем разве не в кубах измеряется?
Решение
объём прямоугольного параллелепипеда:
Определим функцию для поиска экстремума (минимум в данном случае) в виде следующей конкатенации:
— основание вашего бассейна квадрат
— стенками выступают прямоугольники (всего 4 стены)
Потолок (оно же верхнее основание) не прибавляем, ведь у бассейнов нет потолка 
Подставим в функцию определение высоты и значение объёма (32):
Найдём производную и приравняем к нулю:
— не подходит (по интуитивно понятным соображениям)
— не подходит (по интуитивно понятным соображениям)
Стало быть, наша критическая точка:
При проверке достаточных условий можно выявить, что критическая точка является минимумом:
Найдём вторую производную от функции конкатенации:
Подставим критическую точку во вторую производную:
Значение второй производной в критической точке строго больше нуля => Достигается минимум в этой критической точке.
Значит одна из сторон (ширина) стенки бассейна должна быть см.
Подставляем в определение :
Значит высота (или глубина, как угодно) должна быть
И теперь подставляем в функцию конкатенации для нахождения минимальной площади для проведения отделочных работ:
Ответ:
Минимальная ширина = 4 см
Минимальная глубина = 2 см
Минимальная площадь проведения отделочных работ = 48 см^2
Обучайтесь IT-профессиям с гарантией трудоустройства здесь.

Привет всем, нужна помощь с такой задачкой на Pascal ABC: Определить в каких системах счисления (.
Число, заданное в системе счисления с основанием p перевести в систему с основанием q
Число, заданное в системе счисления с основанием p перевести в систему с основанием q
Перевод числа из СС с основанием 10 в СС с основанием N и обратно
Написал перевод из А10 в АN. Помогите оформить обратную процедуру. var a1,b: integer; .
Или воспользуйтесь поиском по форуму:
| Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 11 марта 2009 13:34 | IP |
| neytron40 |      спасибо огромное..эта последняя спасибо огромное..эта последняя найти наименьшее и наибольшее значения функции z=f(x,y) в заданной области. z=x^2-2xy+2y^2+2x , -3 Всего сообщений: 35 | Присоединился: март 2009 | Отправлено: 11 марта 2009 20:54 | IP |
| grignata |       доброго времени суток, помогите найти производную от y=(lg(4x-3))^arccos(4x) доброго времени суток, помогите найти производную от y=(lg(4x-3))^arccos(4x) и решить задачку Из бумажного круга вырезан сектор, а из оставшейся его части склеена коническая воронка. Какой угол должен иметь вырезанный сектор, чтобы объём воронки был наибольшим? спасибо |
| Всего сообщений: 30 | Присоединился: февраль 2009 | Отправлено: 12 марта 2009 10:22 | IP |
| Lipa1990 |      Помогите доделать производные, 16.03 нужно уже сдать. Помогите доделать производные, 16.03 нужно уже сдать. Вообщем нужно найти произвоную 2го порядка от y=sin x/3 и y=(ln x)/Корень(x) 1го порядка от y=xln(x-1) Мои попытки:  — 1е — 1е  — 2е (как от этого найти 2ю производную, незнаю. — 2е (как от этого найти 2ю производную, незнаю. (Сообщение отредактировал Lipa1990 14 марта 2009 15:08) |
| Всего сообщений: 14 | Присоединился: март 2009 | Отправлено: 14 марта 2009 15:02 | IP |
RKI  |      y(x) = sin(x/3) y(x) = sin(x/3) y»(x) = (1/2)*(-3/2)*(x^(-5/2))*(2-lnx) + |
| Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 14 марта 2009 15:59 | IP |
| Lipa1990 |      Спасибо Огромное за решение! Спасибо Огромное за решение! Щас вот думаю, в 2м задании (lnx/sqrt(x)), нужно найти точки перегиба, для этого необходимо найти корни управнения. Что подставить чтоб уравнение = 0 ? + еще 1 вопросик в 1м задании нужно вычислить значение при указанном значении х: f(x)=sin x/3 f»(3) Подставляем в производную: f(3)=-(sin(3/3))/9 = . просто -sin/9 ? |
| Всего сообщений: 14 | Присоединился: март 2009 | Отправлено: 14 марта 2009 17:40 | IP |
RKI  |     
y»(x) = 0 Необходимо анализировать меняет ли знак вторая производная при переходе через точку x = e^(8/3) и x=0 |
| Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 14 марта 2009 18:16 | IP |
RKI  |     
+ еще 1 вопросик Источник Экстремальные задачи с производнойСовершенно верно, иногда от таких задач действительно захватывает дух. Сегодня на уроке мы разберём ещё одно важное приложение производной, имеющее самое что ни на есть прикладное значение! Речь пойдёт о задачах с конкретным геометрическим, физическим, экономическим и т.д. содержанием, в которых исходя из условия, нужно самостоятельно составить функцию и найти её точку минимума либо максимума (и/или, соответственно, минимум либо максимум). Для полноценного изучения урока необходимо уметь находить производные, ПОНИМАТЬ, что такое производная и быть знакомым с понятиями возрастания, убывания и экстремума функции. Таким образом, начинающим рекомендую начать с вышеуказанных статей, чтобы не словить здесь реальный экстрим =) А уже заматеревшие студенты не должны испытать особых трудностей. Разминочная алгебраическая задача и новый материал по ходу решения: Известно, что сумма двух положительных чисел равна 12. Какими должны быть эти числа, чтобы произведение их квадратов было максимальным? Решение: прежде всего, хорошо осознаем, что от нас требуется: в условии фигурируют два положительных числа, причём ни то, ни другое мы не знаем. Но вот их сумма равна 12. Если это, например, 2 и 10, то произведение квадратов И нам нужно отыскать такую пару, для которой данное произведение будет наибольшим. Понятно, что с методом подбора тут замучаешься, к тому же искомые числа ведь могут оказаться и дробными. Поэтому привлечём на помощь могучий аппарат математического анализа. Но сначала вспомним школу и вспомним, как, наивно хлопая ресницами, мы что-то обозначали за «икс»…. Обозначим за Проверим, что их сумма действительно равна 12: Теперь составим функцию произведения их квадратов: Многие читатели уже понимают последующие шаги: далее нужно найти производную, критические точки и обнаружить точку (и), в которой функция И небольшой вопрос техники: производную здесь можно найти несколькими способами. На мой взгляд, удобен следующий вариант: загоняем множители под единую степень и раскрываем там скобки: Итак, По условию оба числа положительны, поэтому значения Проверка вам хорошо знакома: чертим числовую ось, выясняем знаки производной слева и справа от точки Второе достаточное условие экстремумаПусть производная функции если В нашем случае нужно найти вторую производную и вычислить Для удобства дифференцирования утрамбуем предшественницу: Подставим критическое значение Ответ: искомые числа: 6 и 6, при этом максимальное произведение квадратов: Вообще говоря, по условию не требовалось находить само произведение, но по правилам хорошо тона его лучше рассчитать и указать в ответе. К тому же это весьма любопытно. На практике в подавляющем большинстве случаев встречаются задачи с геометрическим смыслом, и поэтому основная часть урока будет посвящена именно им. Начнём с несложного типового примера, который почему-то довольно часто вызывает проблемы: Найти наименьшее расстояние между параболой Решение: вот, пожалуйста, самый что ни на есть практический смысл – представьте, что вам нужно пройти от дороги к дороге. Совершенно понятно, что в отсутствии препятствий это наиболее выгодно осуществить по кратчайшему пути. Поскольку условие запрашивает наименьшее расстояние, то, очевидно, нам нужно составить функцию В нашем случае Таким образом: Дифференцируем по обычным правилам, невзирая на модуль: Проверим выполнение достаточного условия экстремума. Оцените, насколько второе достаточное условие приятнее и удобнее 1-го: Искомая «дорога» изображена малиновым отрезком на чертеже. Ответ: Физики в лирике могут найти ординату точки Следующая задача для самостоятельного решения: Из куска проволоки длиной 30 см требуется согнуть прямоугольник наибольшей площади. Каковы размеры этого прямоугольника? Давайте немного проанализируем условие: Что требуется найти? Очевидно, длину и ширину – это «традиционные» характеристики, определяющие прямоугольник. Какую функцию нужно составить? Наверное, многие уже поняли данную закономерность: Требуется найти минимальную/максимальную площадь? Составляем функцию площади; Напоминаю, что периметр – это длина границы фигуры, в данном случае – сумма длин сторон прямоугольника. Кстати, задачу легко переформулировать «чисто математически»: «Найти прямоугольник максимальной площади, если его периметр равен 30 см» Выполните схематический чертёж, подумайте, что обозначить за «икс» (впрочем, чего тут думать), составьте функцию площади Краткое решение и ответ в конце урока. После простых разогревающих заданий рассмотрим что-нибудь поосновательнее: На странице книги печатный текст должен занимать (вместе с промежутками между строк) 192 Решение: разруливаем задачу по той же логической схеме: Что требуется найти? Наиболее выгодные размеры страницы. А страница обычно имеет форму прямоугольника. Коль скоро речь идёт об экономии бумаги, то, очевидно, нужно найти такую ширину и высоту листа, чтобы его площадь была минимальна. Из чего следует, что нам необходимо составить функцию площади страницы. Причём условие жёстко задаёт размеры полей, а вот под область печати отведено 192 Учитывая известные значения полей, найдём ширину всего листа: И его высоту: Составим функцию площади листа и сразу подготовим её для дифференцирования: Найдём критические точки: Точка Проверим выполнение достаточного условия экстремума: Таким образом, размеры оптимального листа: Ответ: ширина оптимальной страницы: Как видите, основная трудность состоит в том, чтобы разобраться в условии и составить нужную функцию. И в преодолении этой трудности здОрово помогает чертёж. Поэтому всегда стараемся выполнить схематический чертёж или хотя бы рисунок. Даже в таких простых случаях, как в Задаче №3, не говоря уже о только что разобранном примере. Следующее задание для самостоятельного решения: В полукруг радиуса Просто и со вкусом. И снова несколько подсказок, которые полезно иметь в виду и при решении других задач: ! Во-первых, обратите внимание, что условие сформулировано в общем виде и величина ! Во-вторых, выполните схематический чертёж, который здесь очень прост: одна из сторон прямоугольника лежит на диаметре полукруга, а вершины противоположной стороны – на полуокружности. Очевидно, что в полукруг можно вписать бесконечно много прямоугольников и ваша задача найти такой, периметр которого максимален. Какую функцию нужно составлять, надеюсь, всем понятно. Подумайте, что удобнее обозначить за «икс» и, кроме того, освежите в памяти теорему Пифагора. ! В-третьих, задачу можно решить в разных стилях. Образец решения оформлен «исключительно геометрически», однако есть и такой вариант: начертить полукруг в декартовой системе координат – в верхней полуплоскости центром в точке ! И, в-четвёртых, эта задача о том, что иногда совсем не обязательно «разбивать лоб» о новый материал 😉 Если вам показался слишком сложным 2-й достаточный признак экстремума, то никто ведь не запрещает использовать 1-й достаточный признак – определите знаки первой производной слева и справа от критической точки Наш урок в самом разгаре и настало время разобрать задачи, которые встречались в моей практике без преувеличения десятки раз: Определите размеры открытого бассейна объемом Решение: представили бассейн. Квадратное дно. Стены. Размеры бассейна однозначно определяются его длиной и шириной, которые в данном случае совпадают (по условию дно квадратное) и глубиной (высотой стенки). Требуется найти такие размеры бассейна, чтобы на облицовку его поверхности ушло наименьшее количество материала (например, плитки). Из чего следует, что нам нужно составить функцию суммарной площади дна и 4 стен. Изобразим на чертеже развёртку бассейна – его дно и 4 стенки, которые аккуратно лежат рядышком: По условию, объём бассейна равняется 32 кубическим метрам. Даже не вспоминая и не разыскивая соответствующую формулу, нетрудно сообразить, что объём прямоугольного параллелепипеда – это произведение площади его «дна» на высоту: В нашем случае: Составим функцию суммарной площади дна и четырёх одинаковых стен бассейна: Найдем критические точки: Проверим выполнение достаточного условия экстремума: Таким образом: Ответ: сторона оптимального бассейна: 4 м, глубина: 2 м; при этом минимальная площадь облицовки Кстати, это решение совсем не очевидно – так, например, на оптимальный вариант с успехом претендует «лягушатник» размером Аналогичная задача про суровые челябинские шпроты: Каковы должны быть размеры консервной банки цилиндрической формы, чтобы на её изготовление пошло наименьшее количество материала, если объем банки 0,5 литра? Но перед тем как решать, пожалуйста, ознакомьтесь с парой полезных замечаний: Во-первых, литр – это единица объёма. Я специально заострил внимание на физике, поскольку на обывательском уровне литр очень часто неверно отождествляют с килограммом (единицей массы). Ощутите разницу – пол-литровая банка кильки и та же банка, наполненная гвоздями. Один литр равен одному кубическому дециметру или тысяче кубических сантиметров: А теперь очень важный момент: так как размеры банки, очевидно, выразятся в сантиметрах, то 0,5 литра следует сразу перевести в кубические сантиметры! К слову, что это за размеры? Цилиндр стандартно определяется радиусом основания площадь круга: И в который раз остановлюсь на важном принципе эффективного изучения математики: не зубрите формулы (без крайней необходимости, конечно). В частности, позабытую площадь боковой поверхности цилиндра несложно вывести даже в уме: представьте стенку консервной банки без дна и крышки. Сделайте вертикальный разрез и расправьте боковину на столе. В результате получился прямоугольник, одна из сторон которого, понятно, равна высоте банки Решение проводится по аналогии с Задачей 6, примерный образец в конце урока. Закрепим типовик своего рода обратными задачами: Определить наибольшую вместимость цилиндрического бака, если его площадь поверхности (без крышки) должна равняться Решение: в данном случае всё наоборот – известна площадь поверхности От какой переменной искать функцию объёма? В соответствующей формуле наиболее «наворочен» радиус, поэтому логично попытаться составить функцию Сумма площадей дна (не забываем, что крышка отсутствует!) и боковой поверхности в точности равна известному значению: Таким образом: Найдём критические точки: Геометрическому смыслу задачи, разумеется, удовлетворяет положительный корень
При этом высота бака: Ответ: радиус основания оптимального бака: Решение в общем виде, бывает, кажется непривычным, однако оцените его универсальность – теперь достаточно лишь подставить конкретное значение площади и сразу рассчитать размеры оптимального цилиндра. Успокоительное задание для самостоятельного решения: Прямоугольный лист картона имеет размеры Краткое решение и ответ в конце урока. Помимо рассмотренных выше геометрических объектов, на практике также можно встретить треугольники, трапеции, шары, конусы и т.д., но это более редкие гости (что касаемо забытых формул – справочники в помощь). К сожалению, нельзя объять необяътное, и поэтому в рамках этой статьи я ограничился самыми распространёнными примерами. И действительно, задач ведь придумать можно очень много – и всех их не перерешаешь, главное, чтобы вы хорошо поняли принципы и методы решения, которые я постарался изложить максимально пОлно и качественно. Кроме того, существуют экстремальные задачи физического, химического, экономического и др. содержания, однако по причине отсутствия таковых в моей коллекции кот даже и не плакал. Но, понимая, что такое производная и обладая элементарной техникой дифференцирования, вы не должны испытать серьёзных затруднений с этими задачами, хотя для их решения, конечно, нужно разобраться и в самой физике/химии/экономике или иной предметной области. Решения и ответы: Пример 3: Решение: найдем полупериметр прямоугольника: Пример 5: Решение: выполним чертёж: Пример 7: Решение: составим функцию площади полной поверхности цилиндра Пример 9: Решение: пусть Автор: Емелин Александр (Переход на главную страницу)
Источник |


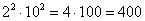 ;
; 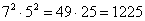 и т.д.
и т.д.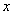 одно из чисел. Тогда второе число будет равно:
одно из чисел. Тогда второе число будет равно: 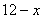
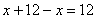 – а ведь и правду говорят, что всё гениальное просто =)
– а ведь и правду говорят, что всё гениальное просто =)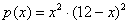
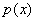 достигает максимума (если таковые, конечно, вообще существуют).
достигает максимума (если таковые, конечно, вообще существуют).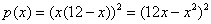 , после чего дифференцируем сложную функцию:
, после чего дифференцируем сложную функцию: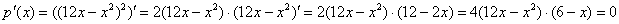
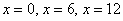 – критические точки.
– критические точки.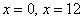 сразу исключаем из рассмотрения. Осталось проверить достаточное условие экстремума для точки
сразу исключаем из рассмотрения. Осталось проверить достаточное условие экстремума для точки  и выяснить, достигает ли там функция
и выяснить, достигает ли там функция 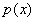 минимума либо максимума. А может статься, и ничего не достигает.
минимума либо максимума. А может статься, и ничего не достигает.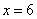 и выносим вердикт. Так решать можно, и это будет правильным решением, но есть и другой путь!
и выносим вердикт. Так решать можно, и это будет правильным решением, но есть и другой путь!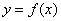 равна нулю в критической точке
равна нулю в критической точке 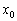 :
: 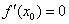 и пусть там существует вторая ненулевая производная:
и пусть там существует вторая ненулевая производная: 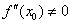 . Тогда:
. Тогда: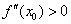 , то функция
, то функция 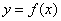 достигает минимума в точке
достигает минимума в точке 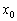 ;
; 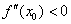 , то – максимума.
, то – максимума.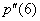 – если окажется, что
– если окажется, что 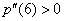 , то
, то 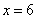 является точкой минимума; если же
является точкой минимума; если же 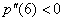 – то точкой максимума.
– то точкой максимума.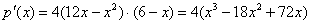 и незамедлительно оценим это удобство:
и незамедлительно оценим это удобство: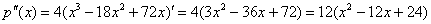
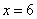 :
: 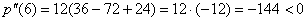 , значит, функция
, значит, функция 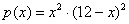 достигает максимума в данной точке:
достигает максимума в данной точке: 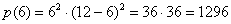
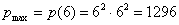
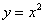 и прямой
и прямой 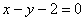
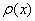 расстояния между параболой
расстояния между параболой 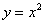 и прямой
и прямой 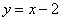 . За аргумент этой функции принимаем абсциссу точки
. За аргумент этой функции принимаем абсциссу точки 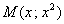 , которая принадлежит параболе и «свободно перемещается по ней»:
, которая принадлежит параболе и «свободно перемещается по ней»: 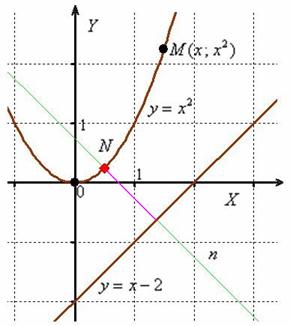
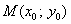 до прямой
до прямой 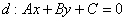 :
: 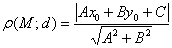
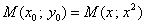 (т.е.
(т.е. 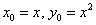 );
); 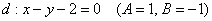 .
.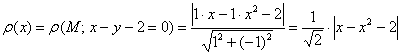 – функция расстояния между параболой и прямой, зависящая от абсциссы точки параболы.
– функция расстояния между параболой и прямой, зависящая от абсциссы точки параболы.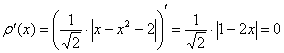
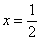 – критическая точка
– критическая точка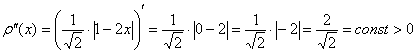 для всех «икс». В частности:
для всех «икс». В частности: 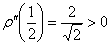 , следовательно, функция
, следовательно, функция 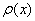 достигает минимума в точке
достигает минимума в точке 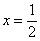 :
: 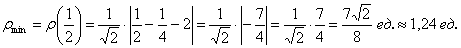
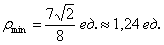
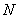 , уравнение нормали
, уравнение нормали 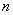 и её точку пересечения с прямой
и её точку пересечения с прямой 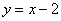 . Кстати, почему кратчайший путь проходит именно по нормали? Приложите ребро ладони к прямой
. Кстати, почему кратчайший путь проходит именно по нормали? Приложите ребро ладони к прямой 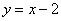 и начните плавно сдвигать его к параболе: первая точка, которой вы коснётесь – будет в точности точка
и начните плавно сдвигать его к параболе: первая точка, которой вы коснётесь – будет в точности точка 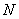 , ваша рука займёт положение касательной к графику функции
, ваша рука займёт положение касательной к графику функции 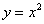 в данной точке, а расстояние между двумя прямыми как раз и определится малиновым отрезком нормальной прямой.
в данной точке, а расстояние между двумя прямыми как раз и определится малиновым отрезком нормальной прямой.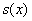 – и дальше по накатанной.
– и дальше по накатанной.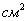 . Верхнее и нижнее поля занимают по 4 см, левое и правое – по 3 см. Если принимать во внимание только экономию бумаги, то каковы должны быть наиболее выгодные размеры страницы?
. Верхнее и нижнее поля занимают по 4 см, левое и правое – по 3 см. Если принимать во внимание только экономию бумаги, то каковы должны быть наиболее выгодные размеры страницы?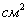 и её размеры могут быть произвольными (заштрихованный прямоугольник на схематическом чертеже):
и её размеры могут быть произвольными (заштрихованный прямоугольник на схематическом чертеже): 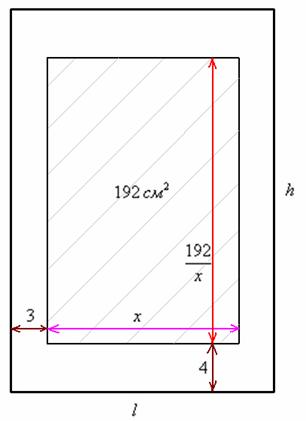
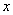 ширину области печати (малиновый отрезок) (можно обозначить высоту – получится равноценное решение). Тогда высота области печати:
ширину области печати (малиновый отрезок) (можно обозначить высоту – получится равноценное решение). Тогда высота области печати: 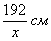 (красный отрезок).
(красный отрезок).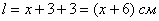
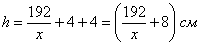
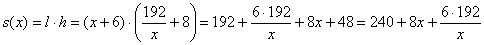
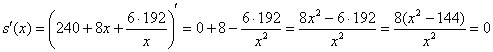
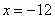 не удовлетворяет геометрическому смыслу задачи, а вот значение
не удовлетворяет геометрическому смыслу задачи, а вот значение 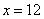 куда более интересно.
куда более интересно.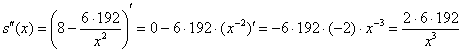
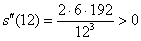 (считать тут совсем не обязательно), значит, функция
(считать тут совсем не обязательно), значит, функция 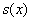 достигает минимума в точке
достигает минимума в точке 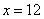 .
.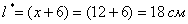 ;
; 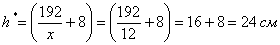 ;
; 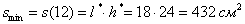
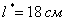 , её высота:
, её высота: 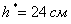 ; при этом минимальная площадь:
; при этом минимальная площадь: 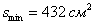
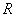 вписать прямоугольник наибольшего периметра
вписать прямоугольник наибольшего периметра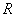 считается известной. Если совсем тяжко, решите задачу с каким-нибудь конкретным значением радиуса, например, с радиусом
считается известной. Если совсем тяжко, решите задачу с каким-нибудь конкретным значением радиуса, например, с радиусом 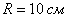 .
.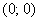 . Далее составить уравнение окружности, выразить функцию верхней полуокружности и рассмотреть переменные координаты вершины прямоугольника, которая на этой полуокружности лежит. Более того, ввиду симметрии фигур относительно оси
. Далее составить уравнение окружности, выразить функцию верхней полуокружности и рассмотреть переменные координаты вершины прямоугольника, которая на этой полуокружности лежит. Более того, ввиду симметрии фигур относительно оси 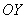 задачу можно решить в 1-й координатной четверти, т.е. изобразить лишь четвертинку круга (но затем не забыть удвоить одну из сторон прямоугольника). Кому как удобнее.
задачу можно решить в 1-й координатной четверти, т.е. изобразить лишь четвертинку круга (но затем не забыть удвоить одну из сторон прямоугольника). Кому как удобнее.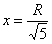 на промежутке
на промежутке 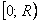 и сделайте вывод.
и сделайте вывод.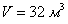 , имеющего форму прямоугольного параллелепипеда с квадратным дном, на облицовку стен и дна которого уйдет наименьшее количество материала.
, имеющего форму прямоугольного параллелепипеда с квадратным дном, на облицовку стен и дна которого уйдет наименьшее количество материала.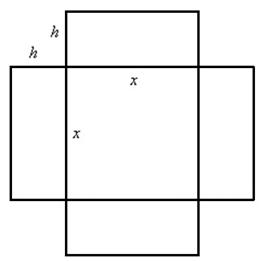
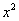 . Осталось выразить
. Осталось выразить 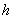 – высоту стены и найти её площадь
– высоту стены и найти её площадь 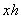 .
.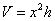
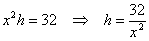 .
.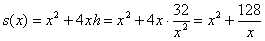
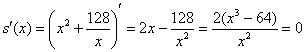
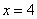 – критическая точка.
– критическая точка.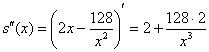
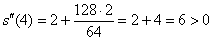 , значит, функция
, значит, функция 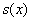 достигает минимума в точке
достигает минимума в точке 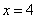 .
.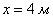 ;
; 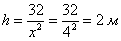 ;
; 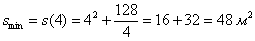 .
.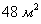 .
.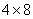 глубиной 1 метр, и «на глазок» очень трудно определить, что выгоднее – ведь площадь облицовки последнего лишь ненамного больше:
глубиной 1 метр, и «на глазок» очень трудно определить, что выгоднее – ведь площадь облицовки последнего лишь ненамного больше: 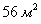 . И да – надо отдать должное авторам задач за реалистичность, а то не так уж и редко получаются забавные результаты а-ля бассейн
. И да – надо отдать должное авторам задач за реалистичность, а то не так уж и редко получаются забавные результаты а-ля бассейн 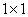 глубиной 32 метра, что называется, купайтесь и не квакайте =)
глубиной 32 метра, что называется, купайтесь и не квакайте =)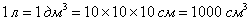
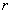 и высотой
и высотой 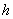 . Во-вторых. Освежим в памяти формулы:
. Во-вторых. Освежим в памяти формулы: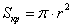
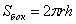
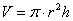
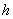 , а другая – длине окружности
, а другая – длине окружности 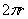 . Площадь же прямоугольника рассчитывается элементарно:
. Площадь же прямоугольника рассчитывается элементарно: 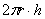
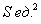
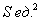 (если трудно, замените
(если трудно, замените 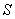 конкретным числом) и требуется определить максимальный объём
конкретным числом) и требуется определить максимальный объём 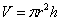 бака.
бака. 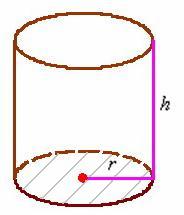
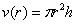 , зависящую именно от него. Нужно только выразить высоту
, зависящую именно от него. Нужно только выразить высоту 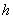 .
.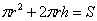 , откуда находим:
, откуда находим: 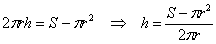
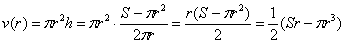
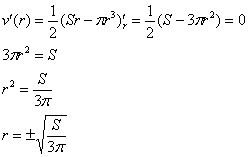
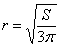 . Проверим выполнение достаточного условия экстремума:
. Проверим выполнение достаточного условия экстремума: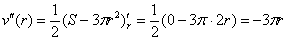
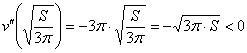 , значит, функция
, значит, функция 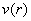 достигает максимума в точке
достигает максимума в точке 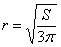 .
.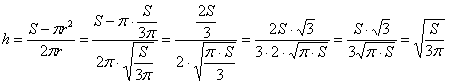
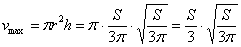
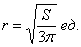 , высота:
, высота: 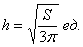 , при этом максимальный объём:
, при этом максимальный объём: 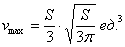
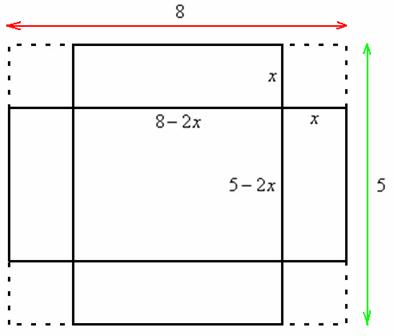
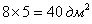 . Требуется вырезать по его углам такие квадраты, чтобы после загибания оставшихся кромок получилась коробка наибольшей вместимости.
. Требуется вырезать по его углам такие квадраты, чтобы после загибания оставшихся кромок получилась коробка наибольшей вместимости.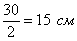 . Обозначим через
. Обозначим через 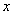 длину стороны прямоугольника (любую). Тогда
длину стороны прямоугольника (любую). Тогда 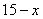 – длина смежной стороны:
– длина смежной стороны: 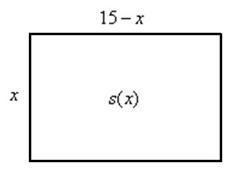
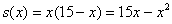 .
. 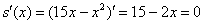
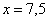 – критическая точка.
– критическая точка. 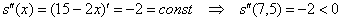 , значит, функция
, значит, функция 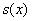 достигает максимума в точке
достигает максимума в точке 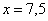 .
. 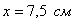 – оптимальная длина стороны прямоугольника, длина смежной стороны:
– оптимальная длина стороны прямоугольника, длина смежной стороны: 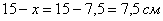 ; при этом максимальная площадь:
; при этом максимальная площадь: 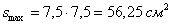
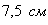 ; при этом максимальная площадь:
; при этом максимальная площадь: 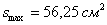 .
.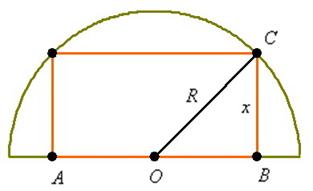
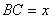 (как вариант, за «икс» можно обозначить
(как вариант, за «икс» можно обозначить 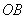 или даже
или даже 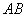 ).
). 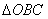 . По теореме Пифагора:
. По теореме Пифагора: 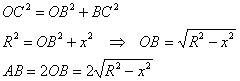
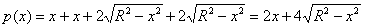
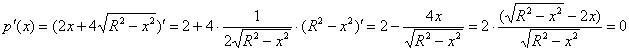 Решим простейшее иррациональное уравнение:
Решим простейшее иррациональное уравнение: 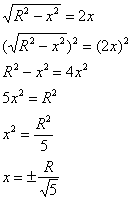
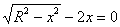 удовлетворяет корень
удовлетворяет корень 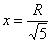 (корень же
(корень же 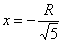 появился в результате возведения обеих частей в квадрат и является посторонним).
появился в результате возведения обеих частей в квадрат и является посторонним). 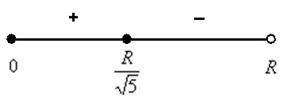
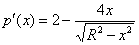 подставляем какое-нибудь значение, лежащее левее точки
подставляем какое-нибудь значение, лежащее левее точки 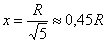 , например,
, например, 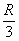 и подставляем какое-нибудь значение из правого интервала – проще всего взять
и подставляем какое-нибудь значение из правого интервала – проще всего взять 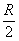 .
. 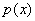 достигает максимума в точке
достигает максимума в точке 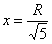 .
. 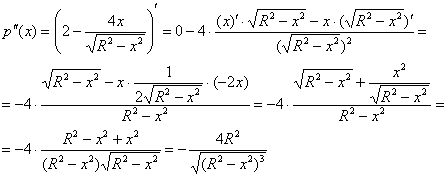
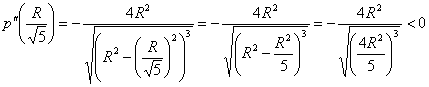 , значит, функция
, значит, функция 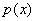 достигает максимума в точке
достигает максимума в точке 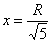 .
. 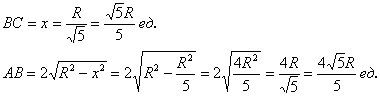
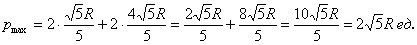
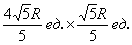 , при этом максимальный периметр:
, при этом максимальный периметр: 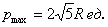
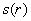 , зависящую от его радиуса. Пусть
, зависящую от его радиуса. Пусть 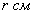 – радиус дна (и крышки) консервной банки:
– радиус дна (и крышки) консервной банки: 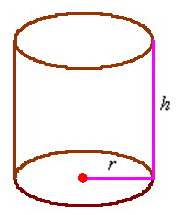
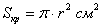 . Столько же и площадь крышки.
. Столько же и площадь крышки. 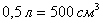 :
: 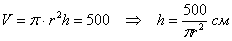
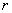 площадь боковой поверхности банки:
площадь боковой поверхности банки: 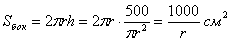
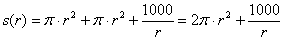
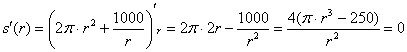
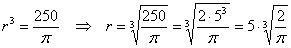 – критическая точка.
– критическая точка. 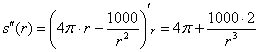
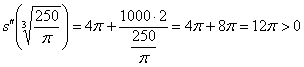 , значит, функция
, значит, функция 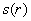 достигает минимума в точке
достигает минимума в точке 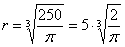 .
. 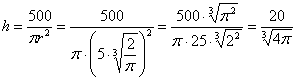
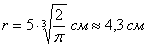 , её высота:
, её высота: 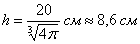
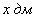 – сторона вырезаемых по углам квадратов (высота будущей коробки). Тогда смежные стороны дна коробки составят
– сторона вырезаемых по углам квадратов (высота будущей коробки). Тогда смежные стороны дна коробки составят 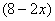 и
и 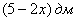 :
: 
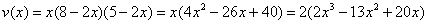
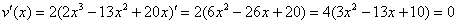
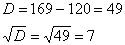
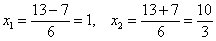 – критические точки. Второе значение не удовлетворяет геометрическому смыслу задачи, поскольку суммарная длина отреза сверху и снизу
– критические точки. Второе значение не удовлетворяет геометрическому смыслу задачи, поскольку суммарная длина отреза сверху и снизу 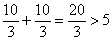 (ширины листа).
(ширины листа). 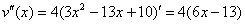
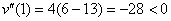 , значит, функция
, значит, функция 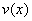 достигает максимума в точке
достигает максимума в точке 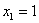 .
. 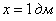 – высота (сторона вырезаемых по углам квадратов);
– высота (сторона вырезаемых по углам квадратов); 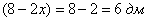 – длина;
– длина; 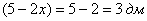 – ширина;
– ширина; 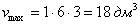 .
. «Всё сдал!» — онлайн-сервис помощи студентам
«Всё сдал!» — онлайн-сервис помощи студентам