- Перемножение эпюр по правилу, методу или способу Верещагина
- Верещагин и его метод, правило или способ
- Площадь и центр тяжести эпюр
- Перемножение простейших эпюр по Верещагину
- Прямоугольник на прямоугольник
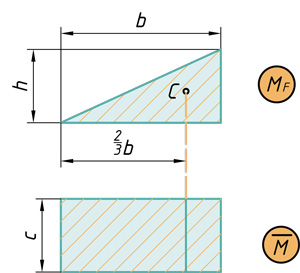
- Прямоугольник на треугольник
- Треугольник на прямоугольник
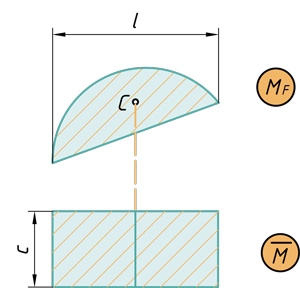
- Параболический сегмент на прямоугольник
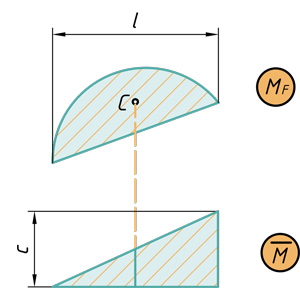
- Параболический сегмент на треугольник
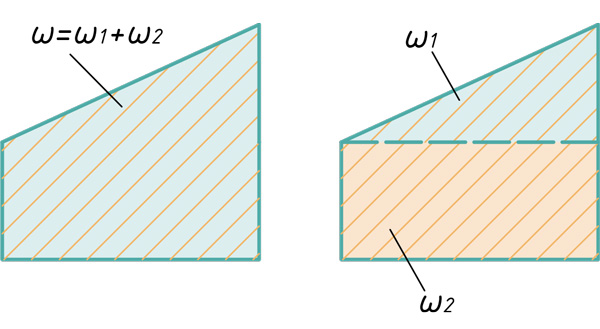
- Расслоение эпюр на простые фигуры
- Прямоугольник и треугольник
- Два треугольника
- Два треугольника и параболический сегмент
- Треугольник, прямоугольник и параболический сегмент
- Пример определения перемещений: прогибов и углов поворотов по Верещагину
- Построение эпюры изгибающих моментов
- Построение единичных эпюр
- Перемножение участков эпюры по Верещагину
- Определение прогиба сечения С
- Определение угла поворота сечения С
- Вопрос 18.Определение перемещений при изгибе. Интеграл Мора. Метод Верещагина.
- 7.4. Определение перемещений способом Верещагина
- 7.5. Примеры определения перемещений методом Мора и способом Верещагина Пример
- Решение
- Определение прогиба балки в середине пролета
- Ход выполнения расчета
- Построение единичной эпюры
- Вычисление прогиба
Перемножение эпюр по правилу, методу или способу Верещагина
Привет! В этой статье будем учиться определять перемещения поперечных сечений при изгибе: прогибы и углы поворотов, по методу (способу, правилу) Верещагина. Причем это правило широко используется не только при определении перемещений, но и при раскрытии статической неопределимости систем по методу сил. Я расскажу, о сути этого метода, как перемножаются эпюры различной сложности и когда выгодно пользоваться этим методом.
Что нужно знать для успешного освоения материалов данного урока? Обязательно нужно уметь строить эпюры изгибающих моментов, т.к. в этой статье будем работать с данной эпюрой.
Верещагин и его метод, правило или способ
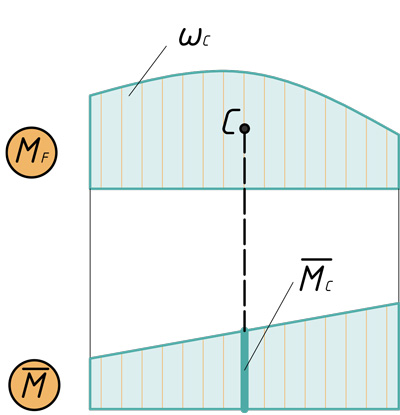
А.К. Верещагин в 1925г. предложил более простой способ решения (формулы) интеграла Мора. Он предложил вместо интегрирования двух функций перемножать эпюры: умножать площадь одной эпюры на ординату второй эпюры под центром тяжести первой. Этим способом можно пользоваться, когда одна из эпюр прямолинейна, вторая может быть как линейной, так и параболической. Кроме того, ордината берется прямолинейной эпюры. Когда эпюры обе прямолинейны, то тут совсем неважно, чью брать площадь, а чью ординату. Таким образом, эпюры по Верещагину перемножаются по следующей формуле:
Проиллюстрировано перемножение эпюр по Верещагину: C — центр тяжести первой эпюры, ωс — площадь первой эпюры, Mc — ордината второй эпюры под центром тяжести первой.
Площадь и центр тяжести эпюр
При использовании метода Верещагина берется не сразу вся площадь эпюры, а частями, в пределах участков. Эпюра изгибающих моментов расслаивается на простейшие фигуры.
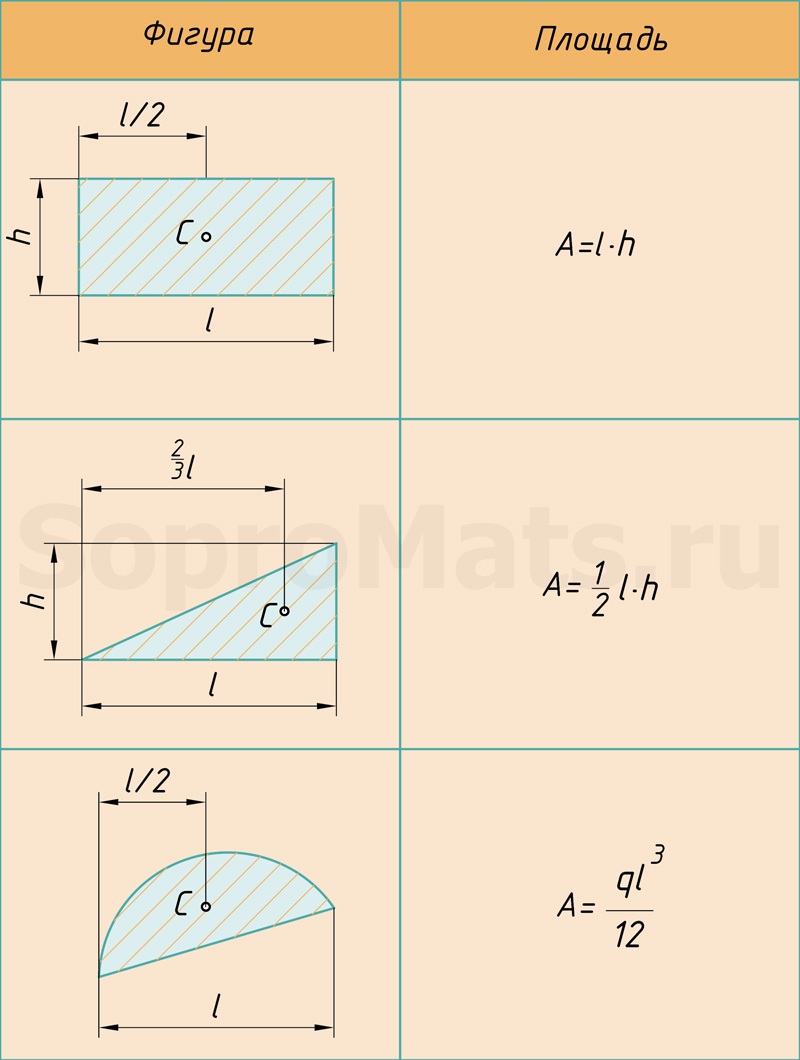
Любой самый сложный участок эпюры можно расслоить на три простейшие фигуры: прямоугольник, прямоугольный треугольник и параболический сегмент.
Поэтому именно с этими фигурами будем дальше работать. Напомню, как вычислить их площадь и где у них находится центр тяжести. Все формулы и размеры оформил в виде таблицы:
Перемножение простейших эпюр по Верещагину
В этом блоке статьи покажу простейшие случаи перемножения эпюр по Верещагину.
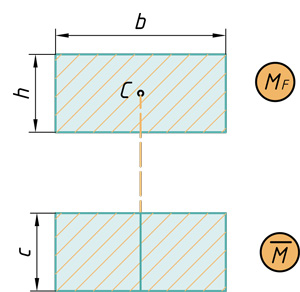
Прямоугольник на прямоугольник
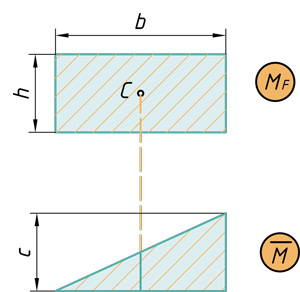
Прямоугольник на треугольник
Треугольник на прямоугольник
Параболический сегмент на прямоугольник
Параболический сегмент на треугольник
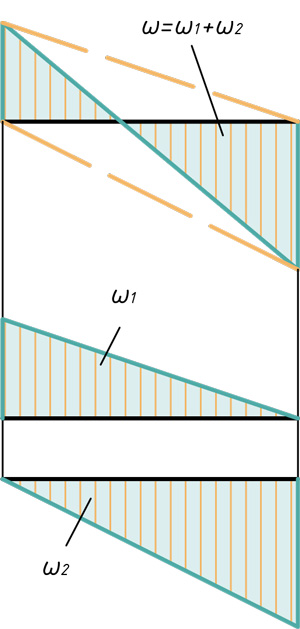
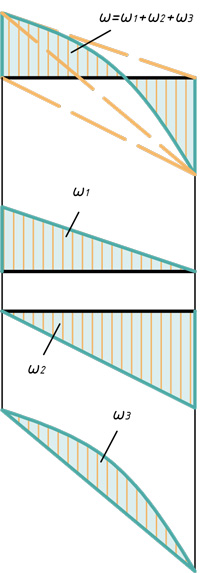
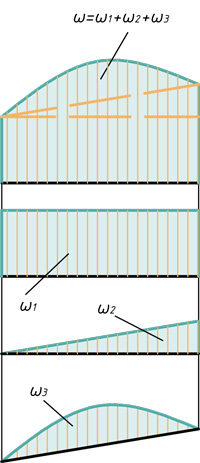
Расслоение эпюр на простые фигуры
В этом блоке статьи покажу способы расслоения эпюр на простые фигуры, для дальнейшего их перемножения по правилу Верещагина.
Прямоугольник и треугольник
Два треугольника
Два треугольника и параболический сегмент
Треугольник, прямоугольник и параболический сегмент
Пример определения перемещений: прогибов и углов поворотов по Верещагину
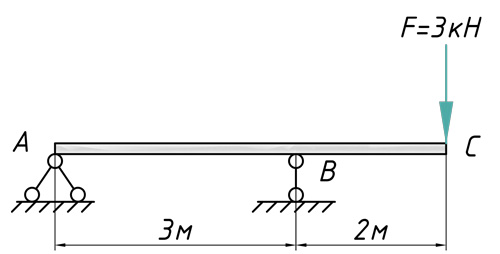
Теперь предлагаю рассмотреть конкретный пример с расчетом перемещений поперечных сечений: их прогибов и углов поворотов. Возьмем стальную балку, которая загружена всевозможными типами нагрузок и определим прогиб сечения C, а также угол поворота сечения A.
Построение эпюры изгибающих моментов
В первую очередь рассчитываем и строим эпюру изгибающих моментов:
Построение единичных эпюр
Теперь для каждого искомого перемещения необходимо приложить единичную нагрузку в ту точку, где это перемещение определяется и построить единичные эпюры:
- для прогибов прикладываются единичные силы.
- для углов поворотов прикладываются единичные моменты.
Все прикладываемые нагрузки являются безразмерными величинами. Причем, направление этих нагрузок неважно! Расчет покажет верное направление перемещений.
Например, после расчета величина прогиба получилась положительной, это значит, что направление перемещения сечения совпадает с направлением ранее прикладываемой единичной силы. То же самое касается и углов поворотов.
Перемножение участков эпюры по Верещагину
После проведения всех подготовительных работ: построения эпюры изгибающих моментов, расслоения ее на элементарные фигуры и построения единичных эпюр от нагрузок, приложенных в местах и направлении искомых перемещений, можно переходить непосредственно к перемножению соответствующих эпюр.
Как уже было написано выше, линейные эпюры можно перемножать в любом порядке, то есть брать площадь любой эпюры: основной или единичной, и умножать на ординату другой. Но обычно, чтобы не путаться в расчетах, площади берут основной эпюры изгибающих моментов, в этом уроке будем придерживаться этого же правила.
Определение прогиба сечения С
Перемножаем соответствующие эпюры слева направо и вычисляем прогиб сечения C по методу Мора — Верещагина:
\[ < V >_< C >=\frac < 1 >< E< I >_ < x >> (\frac < 1 > < 2 >\cdot 6\cdot 3\cdot \frac < 2 > < 3 >\cdot 2+\frac < 1 > < 2 >\cdot 6\cdot 2\cdot \frac < 2 > < 3 >\cdot 2)=\frac < 20кН< м >^ < 3 >>< E< I >_ < x >> \]
Представим, что рассчитываемая балка имеет поперечное сечение в виде двутавра №24 по ГОСТ 8239-89, тогда прогиб балки будет равен:
Определение угла поворота сечения С
Перемножаем соответствующие эпюры слева направо и вычисляем угол поворота сечения C по правилу Мора — Верещагина:
Для закрепления пройденного материала рекомендую изучить примеры, где рассмотрены различные случаи расслоения и перемножения эпюр.
Источник
Вопрос 18.Определение перемещений при изгибе. Интеграл Мора. Метод Верещагина.
Прогиб – линейная деформация, смещение центра тяжести поперечного сечения.
Интеграл Мора позволяет определять прогибы и углы поворота заданного сечения балки, используя интегральное исчисление.


Правило Верещагина. Используется, когда жёсткость при изгибе постоянна вдоль длины. Эпюра изгибающих моментов должна быть линейной. Максимальный прогиб называется стрелой.
Следует иметь в виду, что способы «перемножения» эпюр применимы только при наличии двух условий:
1.Изгибная жесткость балки на рассматриваемом участке должна быть постоянной (EI=Const),
2.Одна из двух эпюр моментов на этом участке (грузовая или единичная) должна быть обязательно линейной. При этом обе эпюры не должны в пределах данного участка иметь перелома.
Δкр= 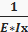

ωp – площадь грузовой эпюры.
k c — ордината в единичном эпюре, соответствует центру тяжести грузовой.
При постоянной жесткости по длине балки EIz для определения прогиба энергетическим методом необходимо вычислять интеграл вида:
.
Допустим, что эпюры изгибающих моментов аналитически выражаются функциями Мz=f1(х), М ’ z´ = f2(х), причем одна из них, например, f1(х) произвольная, а другая f2(х) линейная функция и может быть записана в виде f2(х) = kх+b. Пусть графики этих функций имеют вид представленный на рис. 3.86.
В соответствии с принятыми обозначениями можно записать:
Первый интеграл представляет собой статический момент относительно оси x площади эпюры ограниченной кривой Mz, т.е.
, где
ω – площадь, ограниченная кривой Mz,
хc — координата центра тяжести фигуры ограниченной кривой Mz относительно оси х.
Второй интеграл представляет собой площадь, ограниченную кривой Mz, которую обозначили ω.
Таким образом, искомый интеграл равен произведению площади эпюры Mz на расположенную под ее центром тяжести ординату эпюры Мz´. Важно отметить, что вычисление перемещения способом Верещагина возможно только в том случае, когда, во-первых, эпюры Mz и Мz ´ на рассматриваемом участке не имеют изломов, во-вторых, одна из эпюр описывается линейной зависимостью и именно по ней определяется ордината под центром тяжести другой эпюры yc. Поэтому при вычислении способом Верещагина интеграл Мора по всей длине балки надо заменить суммой интегралов по участкам, в пределах которых эпюра моментов от единичной нагрузки не имеет изломов. Тогда перемещение сечения балки δ:
Таким образом, для вычисления прогибов по способу Верещагина необходимо:
1) построить эпюру изгибающих моментов от заданных нагрузок Mz (основная эпюра);
2) снять внешнюю нагрузку (но сохранить опоры) и приложить в том сечении, в котором определяется перемещение (угол поворота) единичную силу (единичный момент) в направлении искомого.перемещения (угла поворота);
3) построить эпюру изгибающих моментов от единичной нагрузки Мz ´(единичная эпюра);
4) разбить эпюры на участки, в пределах которых отсутствуют изломы эпюр, и для каждого участка вычислить площадь криволинейной эпюры ωi и ординаты эпюр ограниченных линейной функцией под центрами тяжести криволинейных эпюр уci.
5) составить произведения ωi уci и просуммировать:
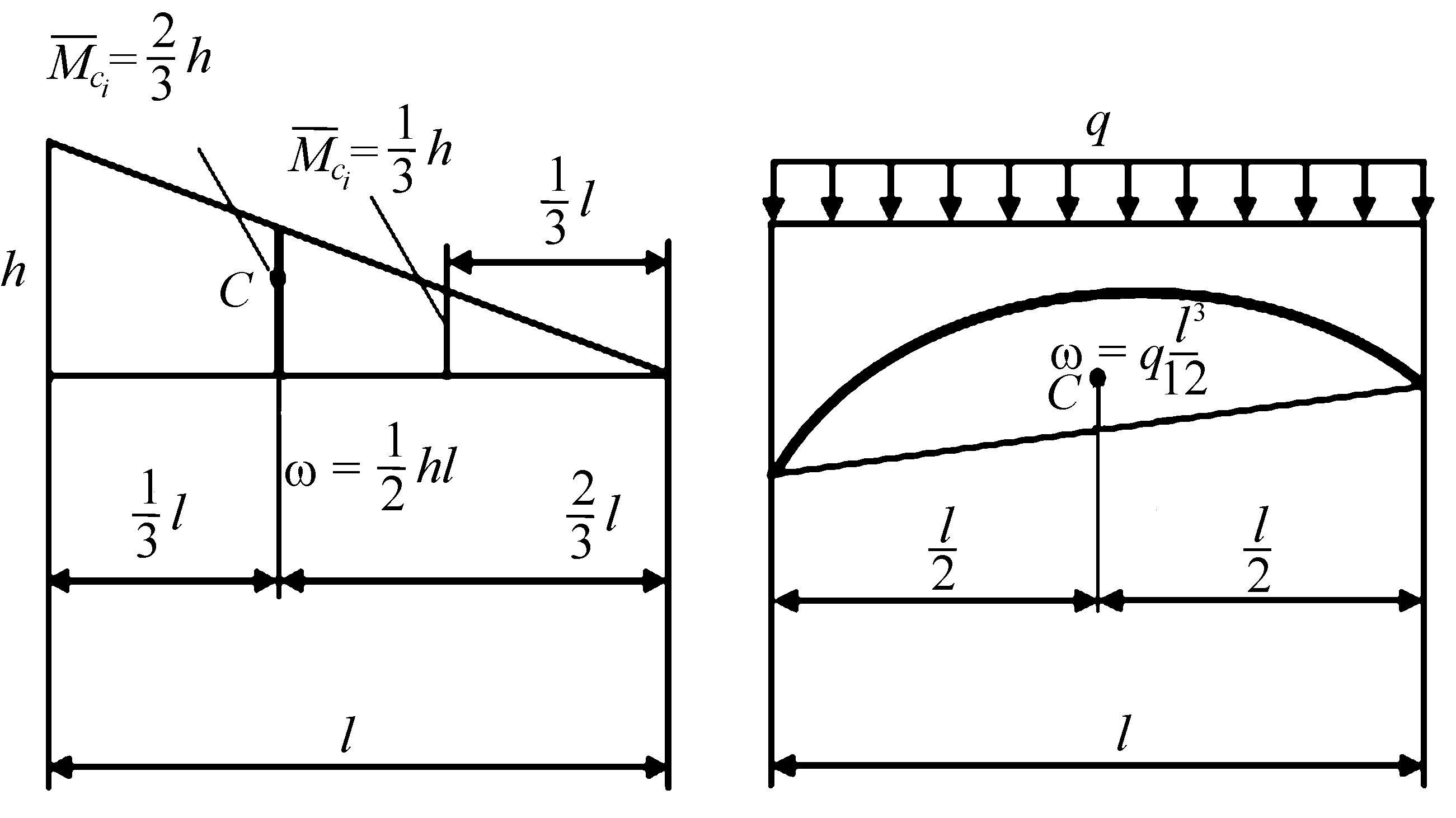
Встречающиеся на практике эпюры изгибающих моментов разбивают на простейшие фигуры: прямоугольник, треугольник и параболический треугольник.
Площади этих фигур и координаты центров тяжести приведены в таблице
| Вид эпюры Mz | Площадь w | Координата центра тяжести xc |
 | ab / 2 | a / 3 |
 | ab / 3 | a/ 4 |
 | ab / 4 | a / 5 |
 | 2ab / 3 | a / 2 |
 | 2ab / 3 | 5a / 8 |
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Источник
7.4. Определение перемещений способом Верещагина
Для конструкций, состоящих из прямолинейных стержней с постоянным поперечным участком на i—м участке, интегралы Мора удобно вычислять по формуле Верещагина:
. (7.14)
Рассматриваемый подход представляет собою графоаналитический способ. В формуле (7.14) 



1. Строят эпюру изгибающих моментов для заданной системы от внешней нагрузки.
2. Составляют схему единичного загружения и строят эпюру изгибающих моментов от единичной нагрузки .
3. Разбивают эпюры 
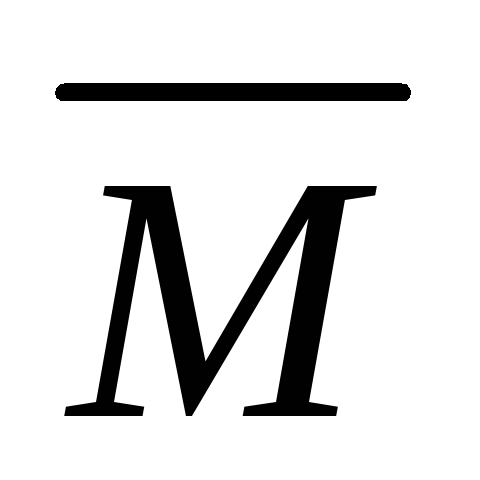
a) под каждым участком эпюры 

б) можно было применить известные формулы для вычисления площадей i участков эпюры и положение центров тяжести этих площадей;
в) изгибная жесткость EJх на каждом участке была постоянной.
4. Вычисляют площади i и ординаты 

5. Применяют формулу Верещагина, суммируя произведения 


Для того чтобы пользоваться формулой Верещагина, надо знать площадь и положение центра тяжести для характерных фигур. На рис. 7.5 приводятся необходимые справочные данные.
7.5. Примеры определения перемещений методом Мора и способом Верещагина Пример
Для заданной стальной балки (рис.7.6, а) подобрать стандартный двутавр из условия прочности. Определить прогиб и угол поворота сечения С, [] = 160 МПа, Е = 210 5 МПа.
Решение
1. Составить уравнения поперечных сил Qy и изгибающих моментов МF от внешней нагрузки и построить их эпюры.
Для консольных балок эпюры Q и М можно строить без определения реакций в заделке, если анализ на участках проводить со стороны свободного конца балки в направлении защемления. Выделим балки и участки балки (см. рис. 7.6, а), запишем выражения внутренних усилий и найдем их значения на границах участков.
Строим эпюру Qy (рис. 7.6, б) и МF (рис. 7.6, в).
2. Подобрать двутавровое сечение из условия прочности по max.
Определяем требуемый момент сопротивления изгибу:
.
Подбираем по ГОСТ 8239–72 двутавр № 27а, у которого Wх = 407,0 см 3 , момент инерции Jх = 5500 см 4 .
3. Определить прогиб сечения С методом Мора.
Составляем схему единичного нагружения, прикладывая к заданной балке безразмерную силу, равную единице в точке С (рис.7.6, г). Разбиваем схему единичного нагружения на такие же участки, что и на схеме грузового нагружения (см. рис. 7.6, а). Записываем для каждого участка выражения изгибающих моментов 

Записываем интегралы Мора на каждом участке и, суммируя результаты, вычисляем прогиб сечения С.
Источник
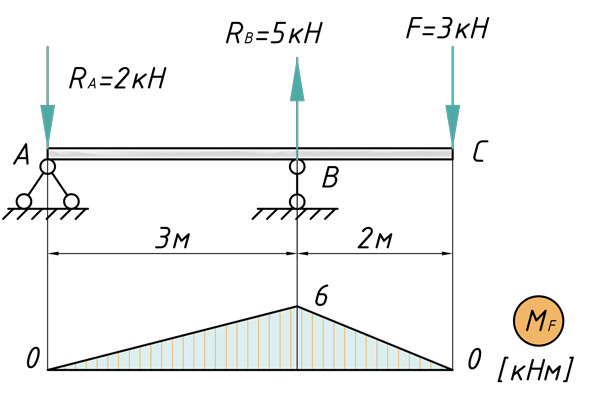
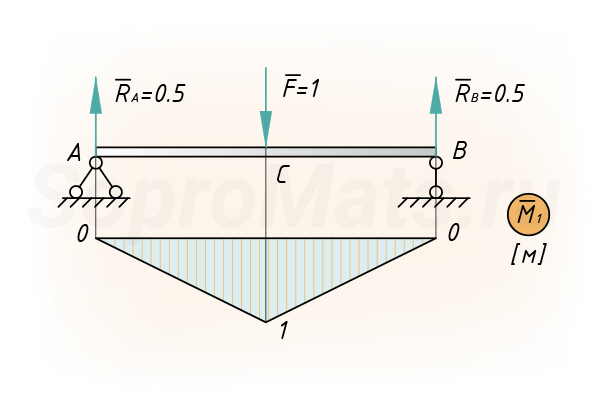
Определение прогиба балки в середине пролета
Для двухопорной двутавровой балки (двутавр №12 по ГОСТ ГОСТ 8239-89) необходимо определить прогиб в середине пролета (сечение C), используя метод Мора — Верещагина. Данные для расчета указаны на схеме.
Ход выполнения расчета
Сначала строим эпюру изгибающих моментов, для рассчитываемой балки:
Расслаиваем эпюру на простейшие фигуры:
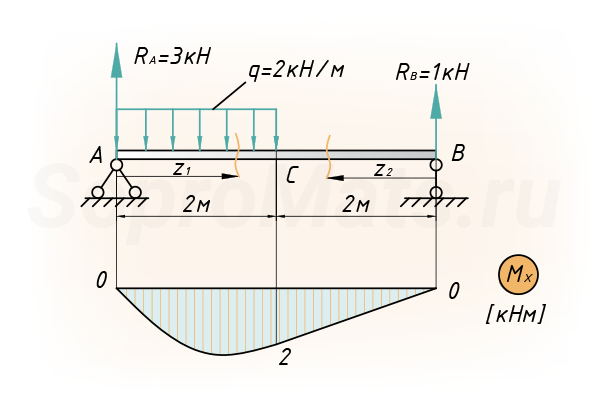
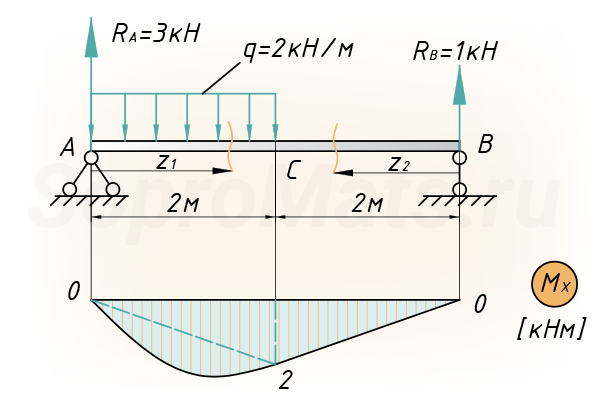
Построение единичной эпюры
Прикладываем единичное усилие по направлению искомого перемещения (в точке С) и строим от этой силы эпюры моментов:
Вычисление прогиба
Вычисляем прогиб сечения C по методу Мора — Верещагина (слева направо):
\[ < V >_< C >=\frac < 1 >< E< I >_ < x >> (\frac < q< \cdot 2 >^ < 3 >> < 12 >\cdot \frac < 1 > < 2 >\cdot 1+\frac < 1 > < 2 >\cdot 2\cdot 2\cdot \frac < 2 > < 3 >\cdot 1+\frac < 1 > < 2 >\cdot 2\cdot 2\cdot \frac < 2 > < 3 >\cdot 1)=\frac < 10кН< м >^ < 3 >>< 3E< I >_ < x >> \]
По сортаменту двутавров выписываем значение момента инерции балки и вычисляем численное значение прогиба:
Источник