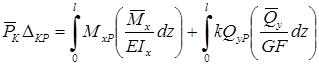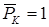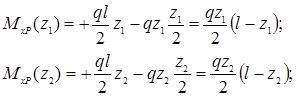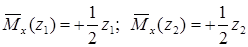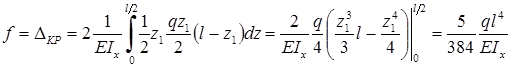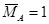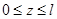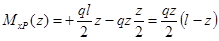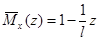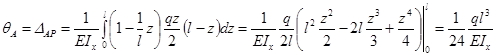Определение перемещений стержневых систем вывод формулы мора

2.2. Определение перемещений в стержневой системе

При расчете статически неопределимых систем, кроме уравне­ний равновесия, как известно, приходится составлять и решать уравнения совместности деформаций системы. Для составления та­ких уравнений необходимо уметь определять перемещения заданной системы. Это приходится часто делать и при расчете статически опреде­лимых систем, которые должны обладать не только достаточной прочностью, но и жесткостью, так как в процессе их эксплуатации нормируются не только напряжения, но и перемещения конструкций.

Таким образом, изучение общих методов определения переме­щений упругих систем является одной из основных задач строи­тельной механики.

При определении перемещений заданной системы очень важ­ным является понятие работы внешних сил на возможных перемещениях, которая при их статическом действии на соору­жение равна сумме половины произведения значения этих сил на величину соответствующего им перемещения. Работа внешних сил на вызванных ими перемещениях может быть выражена через вну­тренние усилия (изгибающие моменты, продольные и поперечные силы), возникающие в поперечных сечениях стержней конструк­ции. На этом основан один из наиболее распространенных спосо­бов определения перемещений — способ, предложенный немецким ученым О. Моpом в 1874г.

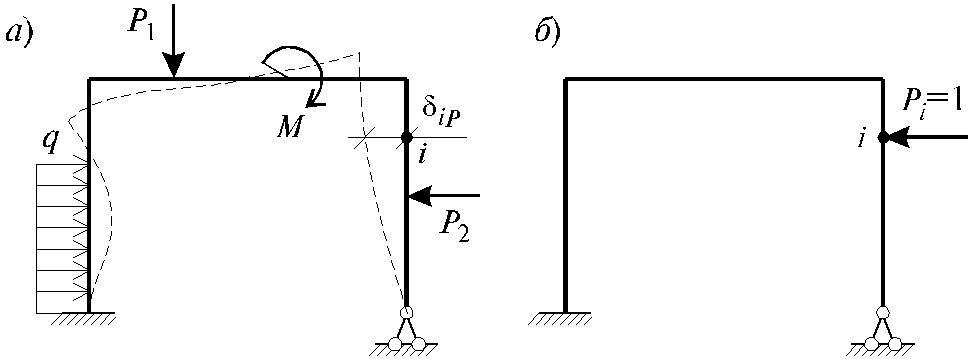
Пусть рассматриваемая заданная стержневая система под влия­нием внешнего воздействия деформируется и требуется определить обобщенное перемещение в i—ой произвольной точке (рис. 2.4) в заранее заданном направлении.

Согласно принципа возможных перемещений, для закреплен­ной системы с идеальными связями, сумма работ всех усилий на любых малых возможных перемещениях равна нулю. Что является необходимым и достаточным условием нахождения равновесного состояния рассматриваемой системы. Для деформируемой системы, в аналитическом выражении начала возможных перемещений, сле­дует учесть работу, как внешних, так и внутренних усилий.

Рассмотрим два состояния системы: одно, возникающее под действием заданной нагрузки (рис. 2.4, а); второе — под действием единичной силы, приложенной в интересующей нас точке i по направлению искомого переме­щения (рис. 2.4, б). Определим возможную работу сил второго со­стояния на перемещениях первого состояния.

Работа внешней силы Р_i = 1:

где d_iP — перемещение i—ой точки по направлению силы Р_i = 1 в первом состоянии, вызванной действием системы внешних сил.

Работа внутренних усилий, как известно из курса “Сопро-тивле­ния материалов” [9], была представлена в виде:

, (2.2)

где , , , , , — усилия в первом и втором сос­тоянии, соответственно; EJ_j , EF_j , GF_j — жесткости на изгиб, рас­тяжение-сжатие и сдвиг, соответственно, для j-ого стержня; h -коэффициент, зависящий от формы поперечного сечения, для прямоугольного сечения h = 1.2.

В силу принципа возможных перемещений: dA + dV = 0, т.е. работа внешних сил равна работе внутренних сил с обратным знаком dV = -dA, далее, учитывая (2.1) и (2.2), получим:

. (2.3)

Это выражение носит название фоpмyлы Моpа. Замечательной особенностью вычисления перемещений по формуле Моpа являет­ся то обстоятельство, что в качестве второго состояния можно ис­пользовать любую систему, образованную из заданной путем отбра­сывания лишних связей, т.е. брать в качестве вспомогательного состояния любую статически определимую систему, полученной из заданной. Это в значительной степени упрощает процедуру вычис­ления перемещения по формуле Мора.

Во многих практических случаях формула Мора может быть значительно упрощена. Например, в статически неопределимых фермах изгибающие моменты и поперечные силы пренебрежимо малы, а продольные силы постоянны по длине каждого стержня. Поэтому для ферм формула Моpа принимает вид:

. (2.4)

В рамах обычно пренебрегают влиянием вторых и третьих чле­нов (2.3), так как эти члены незначительно влияют на величину перемещений:

. (2.5)

Продольные силы вместе c изгибающими моментами учиты­вают в расчете систем, элементы которых испытывают значитель­ные осевые деформации, сравнимые c деформациями от изгибаю­щих моментов, например, в арках, а также при учете податливости отдельных элементов систем, работающих преимущественно на сжатие или растяжение, например, затяжек в рамах или арках.

Интеграл Мора, наряду с методом начальных параметров, явля­ется достаточно мощным инструментом для определения переме­щений стержневых систем. Проиллюстрируем это на примере.

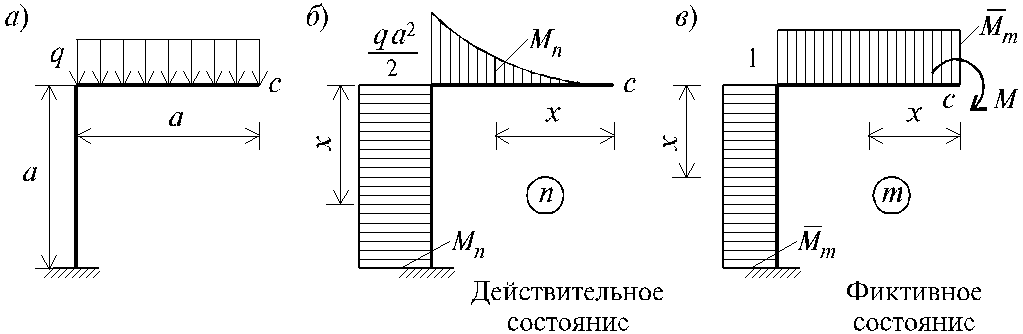
Для ломаного бруса, изображенного на рис. 2.5, а определим угол поворота поперечного сечения С относительно вертикальной оси. Пусть жесткость ригеля в два раза больше жесткости стойки, т.е. EJ_р = 2×EJ_c .

Последовательность расчета следующая:

1) строим эпюру моментов М_n от заданной нагрузки q (эпюра моментов действительного состояния n рис. 2.5, б);

2) строим эпюру моментов М_m при загружении конца консоли единичным моментом M = 1 (эпюра моментов фиктивного состоя­ния m, рис. 2.5, в);

3) выразим изгибающие моменты через переменные абсцис­сы x:

— для ригеля: M_n = —q x 2 /2; M_m = -1; — для стойки: M_n = —q a 2 /2; M_m = -1;

4) применяя формулу перемещений (2.5), найдем искомый угол поворота:

(рад).

Источник

Билет 4

1.Теория напряжений. Круговая диаграмма о.Мора. Вывод формулы.

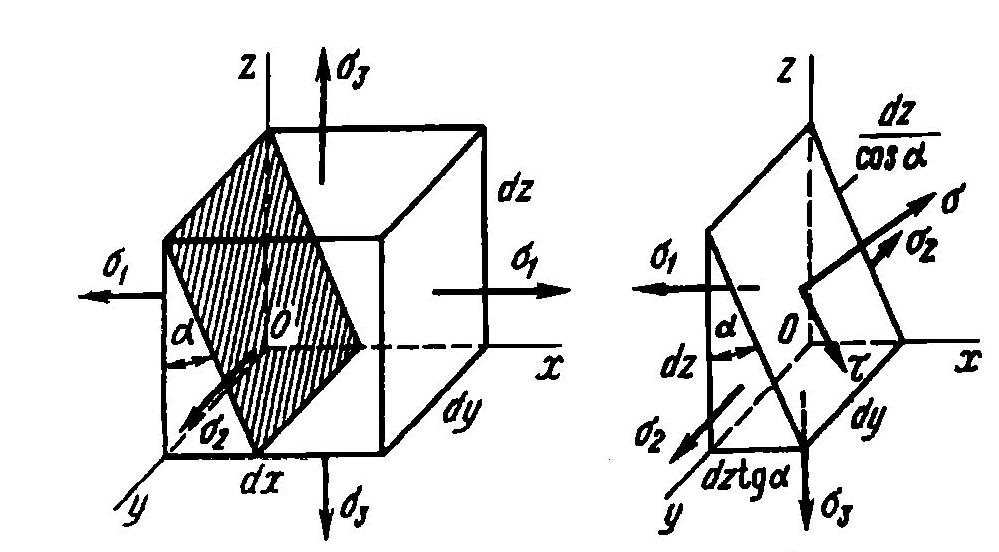
Рассмотрим условия равновесия треугольной призмы (рис). Она образована путем сечения элементарного параллелепипеда

наклонной площадкой, которая независимо от угла наклона αостается параллельной одной из главных осей(y)

П роецируя все силы, действующие на отсеченную призму, на оси параллельные векторам α и τ :

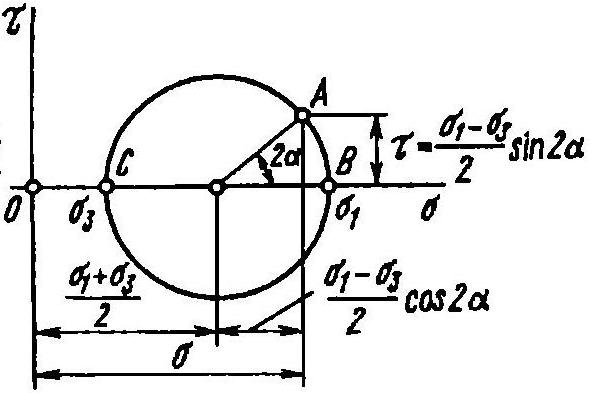
– напряжения в семействе площадок параллельных 1 из гл. осей, можно дать геом. толкование:

; в системе координат,τ это есть ур-ие окружности, центр которой находится на расстоянии ) от нач.координат.. Окружность построенная на отрезке как

на диаметре называется Круговой диаграммой О.Мора. ( ур-ие окр)

2. Учет симметрии при решении статически неопределимых стержневых систем. Показать на примерах.

Билет 5

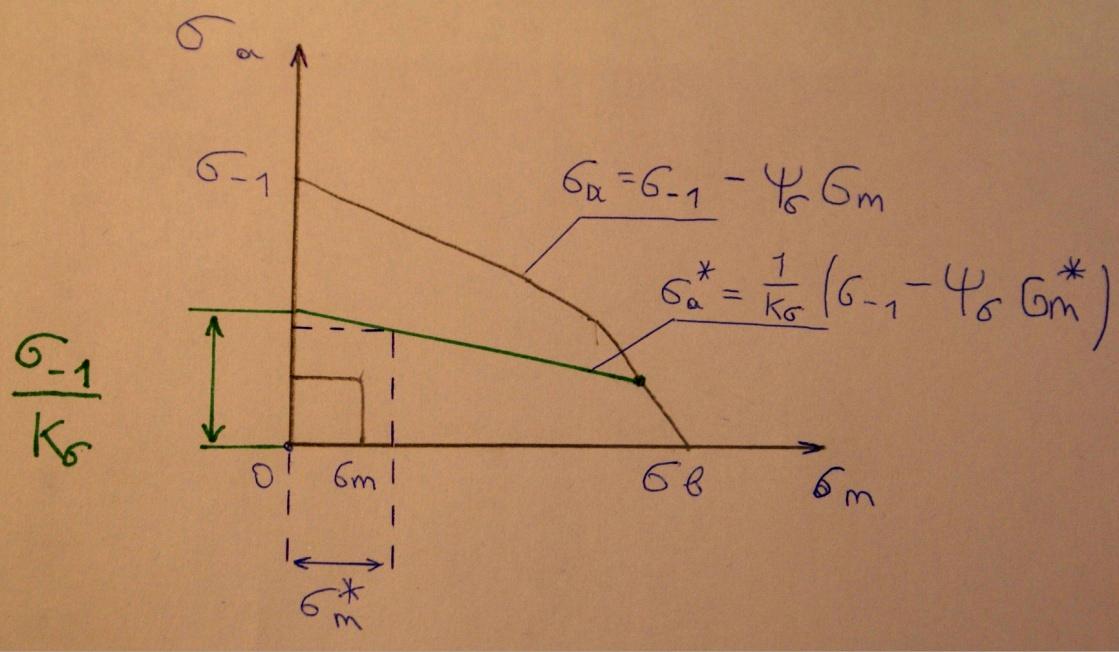
1. Расчеты на прочность при напряжениях, переменных во времени

Большинство деталей в различных машинах подвергаются действию циклически изменяющихся напряжений.

При циклическом изменении напряжений поломка деталей может происходить при напряжениях, значительно меньших, чем предел текучести.

Цикл- совокупность напряжений за период времени.

Циклы с одинаковыми R называются подобными.

Определение коэффициента запаса по выносливости при одноосном напряженном состоянии.

Все полученный формулы применимы только при регулярном нагружении, при котором амплитуда и не меняются.

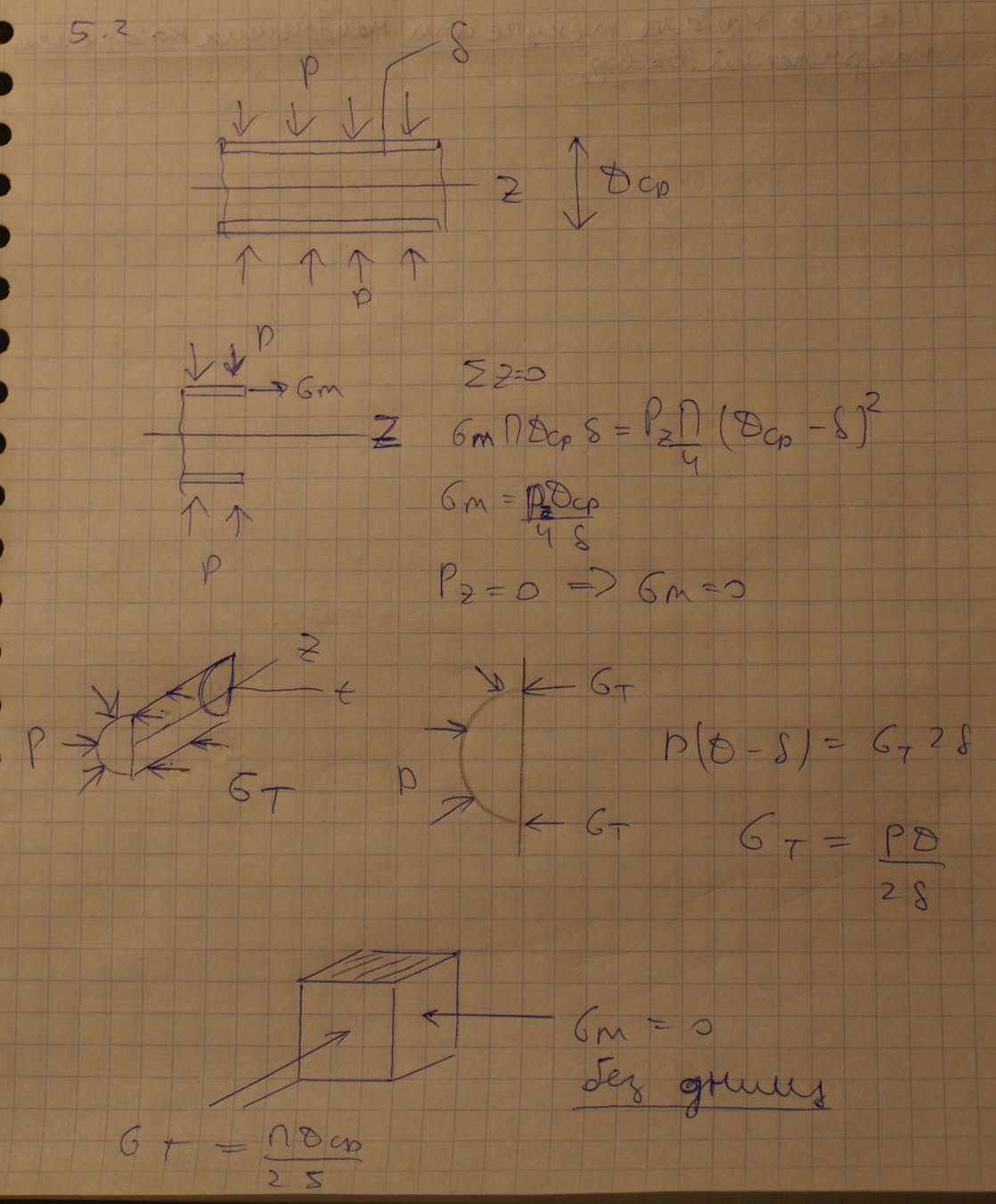
2.Напряжения, возникающие в тонкостенной трубке без днищ, нагруженной внешним давлением.

Билет 6

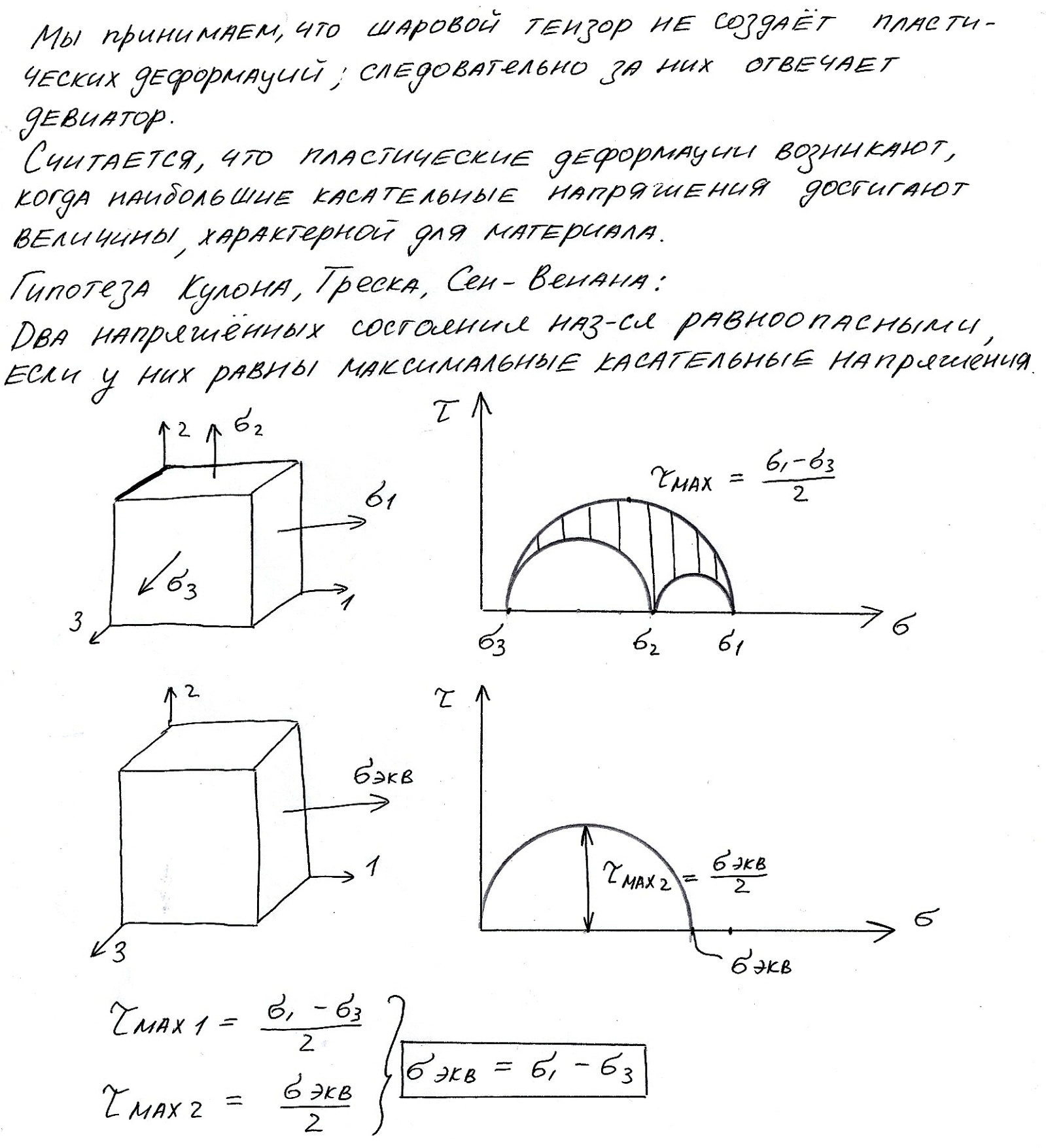
1. Теория начала текучести наибольших касательных напряжений. Вывод.

Мы принимаем, что шаровой тензор не создаёт пластических деформаций; следовательно за них отвечает девиатор.

Считается, что пластические деформации возникают, когда наибольшие касательные напряжения достигают величины, характерной для материала.

Гипотеза Кулона, Треска, Сен-Венана:

Два напряженных состояния называются равноопасными, если у них равны максимальные касательные напряжения.

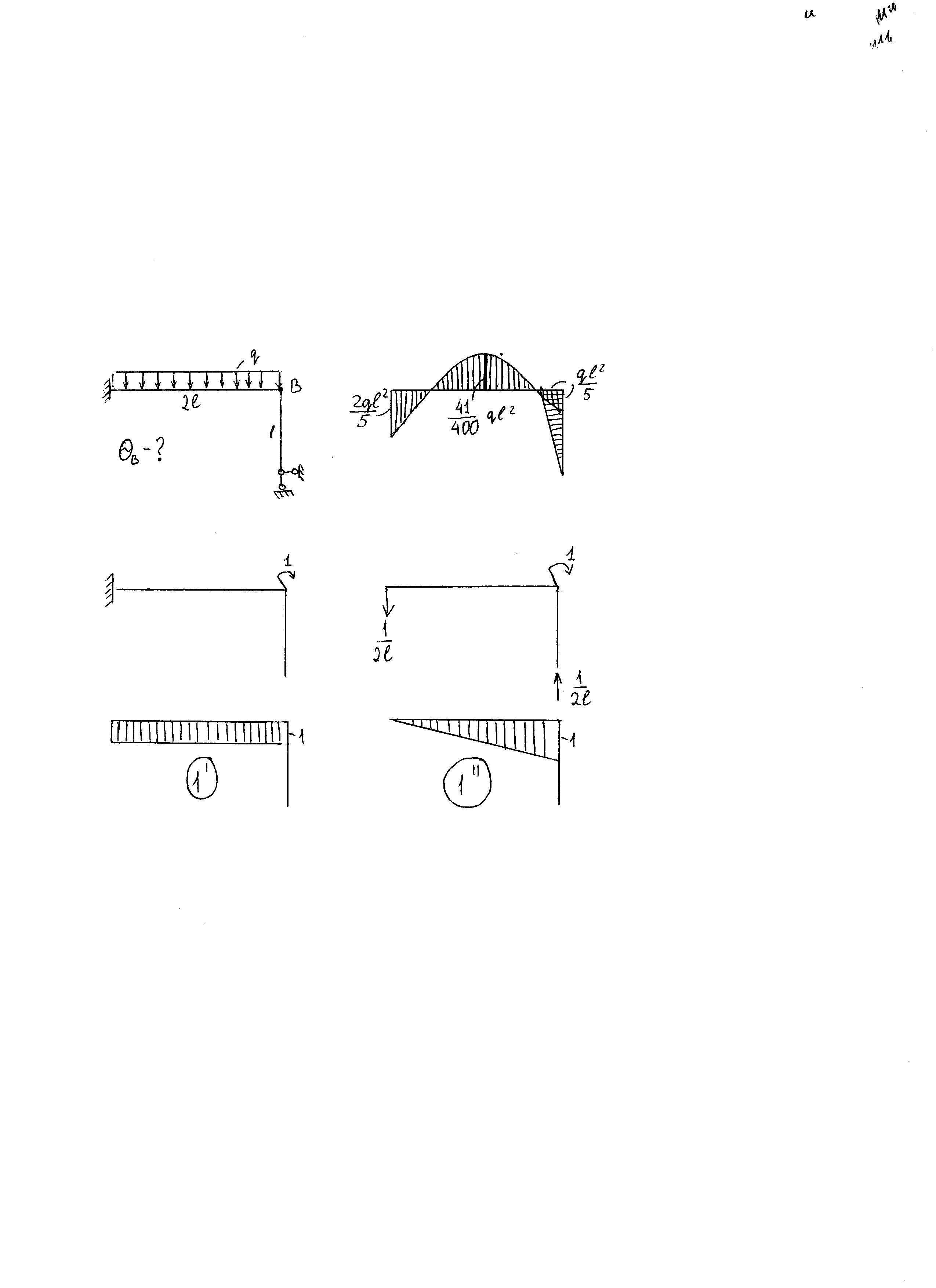
2. Определение перемещений в статически неопределимых стержневых системах

Перемещение ищем после того, как раскрыта статическая неопределённость и построена суммарная эпюра моментов.

Чтобы ещё раз не раскрывать статическую неопределённость, перемещение будем искать не для заданной системы, а для эквивалентной.

Для этого берём любую эквивалентную систему, разгружаем область внешних сил и, согласно интегралам Мора, прикладываем единичный фактор в направлении искомого перемещения.

После перемножаем суммарную эпюру М с эпюрой единичного фактора, используя графоаналитический способ взятия интегралов Мора.

Рассмотрим 2 эквивалентные системы:

Как видно, получили одинаковые результаты, т.е. от выбора эквивалентной системы ничего не зависит.

Источник

Определение прогибов и углов поворотов методом Мора

Интеграл Мора позволяет определять прогибы и углы поворота заданного сечения балки, используя интегральное исчисление. Хотя данный метод предпочтительнее метода начальных параметров, он неудобен из-за необходимости вычисления интеграла. Из интеграла Мора был получен удобное для практического применения правило Верещагина, при котором не нужно вычислять интегралы, а только нужно находить площадь и центр тяжести эпюр.

Получение формулы интеграла Мора

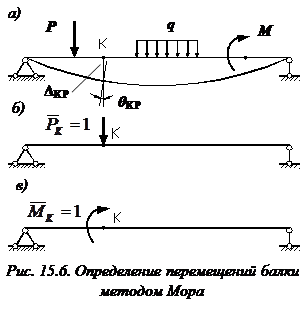
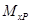
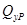
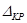
Рассмотрим балку, изображенную на рис. 15.6, а. Обозначим и , соответственно, изгибающий момент и поперечную силу, возникающие в заданной балке от действующей на нее группы нагрузок P. Пусть требуется определить прогиб балки () в точке K.

Введем в рассмотрение вспомогательную балку (та же балка, но нагруженная только единичной силой либо единичным изгибающим моментом). Нагрузим ее только одной силой (рис. 15.6, б). Единичную силу приложим в точке K, где нужно определить прогиб.

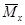
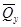
Внутренние усилия, возникающие во вспомогательной балке, обозначим и .

Воспользуемся теперь теоремой о взаимности работ, согласно которой работа внешних сил, приложенных к вспомогательной балке на соответствующих перемещениях заданной балки равна взятой с обратным знаком работе внутренних сил заданной балки на соответствующих перемещениях вспомогательной балки. Тогда .

При определении перемещений в балке, как правило, можно пренебрегать влиянием поперечной силы, ( не учитывать второе слагаемое).

Тогда, учитывая, что , окончательно получим формулу интеграла Мора : .

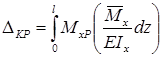
Определение перемещений по формуле интеграла Мора часто называют определением перемещений методом Мора , а саму формулу – интегралом Мора .

Входящие в интеграл Мора изгибающие моменты берутся в произвольном поперечном сечении и поэтому представляют собой аналитические функции от текущей координаты z.

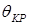
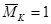
Заметим, что если мы хотим в этой же точке K определить угол поворота поперечного сечения (), то нам необходимо к вспомогательной балке приложить не единичную силу, а единичный момент (рис. 15.6, в).

порядок вычисления перемещений методом Мора:

· к вспомогательной балке в той точке, где требуется определить перемещение, прикладываем единичное усилие. При определении прогиба прикладываем единичную силу , а при определении угла поворота – единичный момент ;

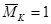
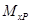
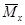
· для каждого участка балки составляем выражения для изгибающих моментов заданной () и вспомогательной () балок;

· вычисляем интеграл Мора для всей балки по соответствующим участкам;

· если вычисленное перемещение имеет положительный знак, то это означает, что его направление совпадает с направлением единичного усилия. Отрицательный знак указывает на то, что действительное направление искомого перемещения противоположно направлению единичного усилия.

Вычисление интеграла Мора пример

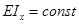
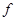
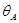
Пусть для шарнирно опертой балки постоянной изгибной жесткости , длиной l, нагруженной равномерно распределенной нагрузкой интенсивностью q (рис. 15.7, а), требуется определить прогиб посредине пролета () и угол поворота на левой опоре ().

определение прогиба с помощью интеграла Мора

В том месте, где нам нужно определить прогиб, к вспомогательной балке прикладываем единичную силу (рис. 15.7, б).

Записываем выражения для изгибающих моментов для каждого из двух участков () заданной и вспомогательной балок:

.

.

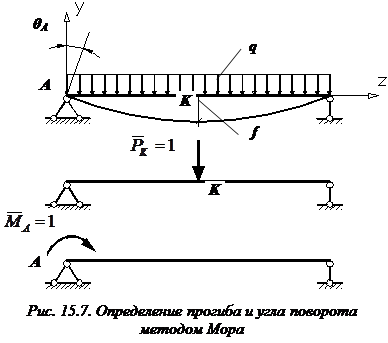
Вычисляем интеграл Мора . Учитывая симметрию балки, получим:

.

Определение угла поворота методом Мора

Нагружаем вспомогательную балку единичным моментом , прикладывая его в том месте, где мы ищем угол поворота (рис. 15.7, в).

Записываем выражения для изгибающих моментов в заданной и вспомогательной балках только для одного участка ():

;

.

Тогда интеграл Мора будет иметь вид:

.

Положительный знак в выражении для угла поворота поперечного сечения балки указывает на то, что поворот сечения происходит по направлению единичного момента .

Источник