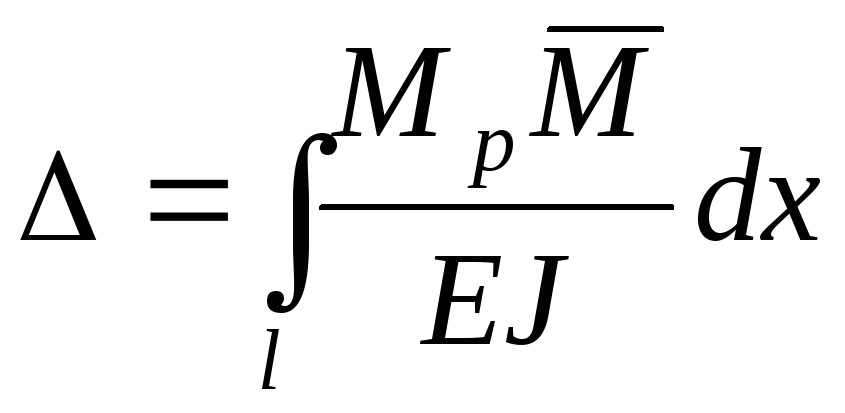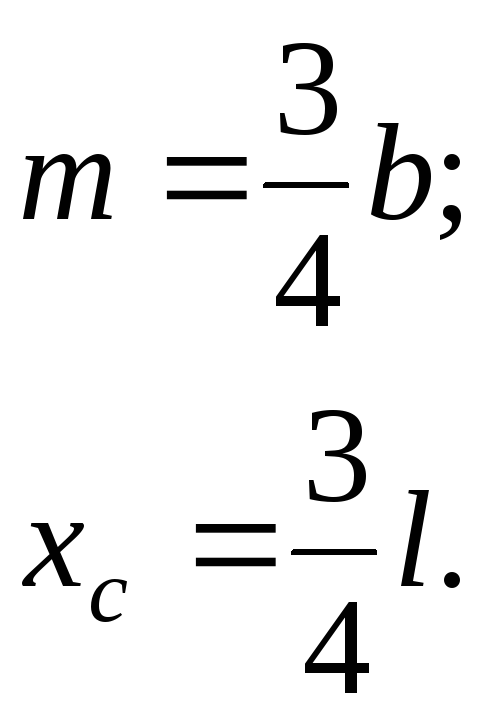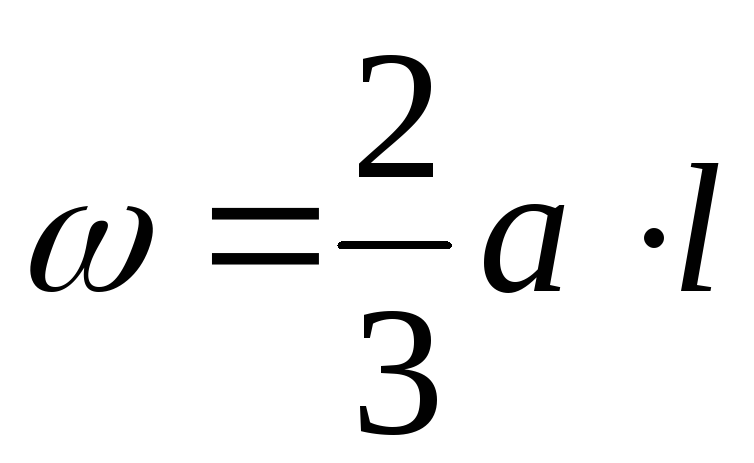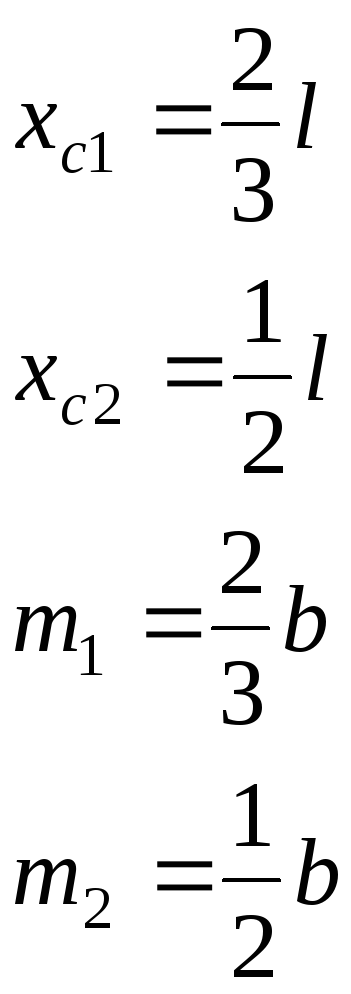- Перемножение эпюр по правилу, методу или способу Верещагина
- Верещагин и его метод, правило или способ
- Площадь и центр тяжести эпюр
- Перемножение простейших эпюр по Верещагину
- Прямоугольник на прямоугольник
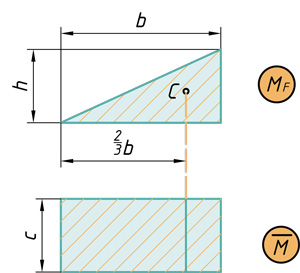
- Прямоугольник на треугольник
- Треугольник на прямоугольник
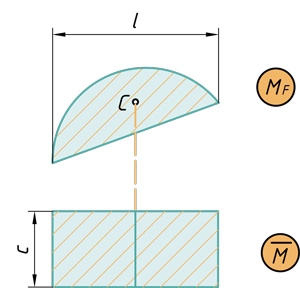
- Параболический сегмент на прямоугольник
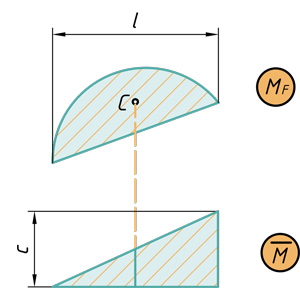
- Параболический сегмент на треугольник
- Расслоение эпюр на простые фигуры
- Прямоугольник и треугольник
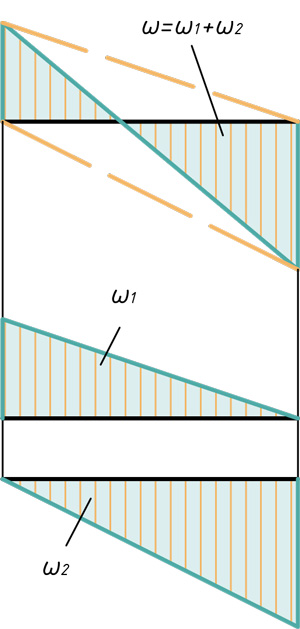
- Два треугольника
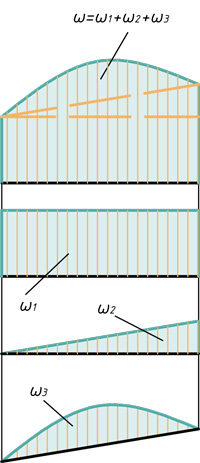
- Два треугольника и параболический сегмент
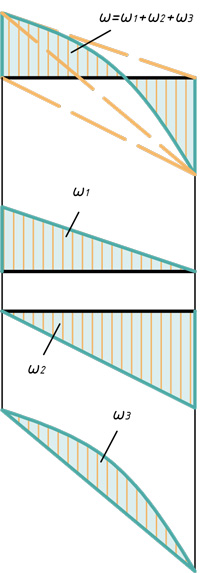
- Треугольник, прямоугольник и параболический сегмент
- Пример определения перемещений: прогибов и углов поворотов по Верещагину
- Построение эпюры изгибающих моментов
- Построение единичных эпюр
- Перемножение участков эпюры по Верещагину
- Определение прогиба сечения С
- Определение угла поворота сечения С
- 1.11. Определение перемещений при изгибе по способу Верещагина
- 2. Правило Мора-Верещагина (графический способ вычисления интеграла Мора)
Перемножение эпюр по правилу, методу или способу Верещагина
Привет! В этой статье будем учиться определять перемещения поперечных сечений при изгибе: прогибы и углы поворотов, по методу (способу, правилу) Верещагина. Причем это правило широко используется не только при определении перемещений, но и при раскрытии статической неопределимости систем по методу сил. Я расскажу, о сути этого метода, как перемножаются эпюры различной сложности и когда выгодно пользоваться этим методом.
Что нужно знать для успешного освоения материалов данного урока? Обязательно нужно уметь строить эпюры изгибающих моментов, т.к. в этой статье будем работать с данной эпюрой.
Верещагин и его метод, правило или способ
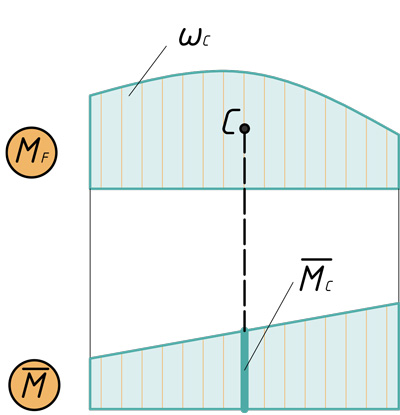
А.К. Верещагин в 1925г. предложил более простой способ решения (формулы) интеграла Мора. Он предложил вместо интегрирования двух функций перемножать эпюры: умножать площадь одной эпюры на ординату второй эпюры под центром тяжести первой. Этим способом можно пользоваться, когда одна из эпюр прямолинейна, вторая может быть как линейной, так и параболической. Кроме того, ордината берется прямолинейной эпюры. Когда эпюры обе прямолинейны, то тут совсем неважно, чью брать площадь, а чью ординату. Таким образом, эпюры по Верещагину перемножаются по следующей формуле:
Проиллюстрировано перемножение эпюр по Верещагину: C — центр тяжести первой эпюры, ωс — площадь первой эпюры, Mc — ордината второй эпюры под центром тяжести первой.
Площадь и центр тяжести эпюр
При использовании метода Верещагина берется не сразу вся площадь эпюры, а частями, в пределах участков. Эпюра изгибающих моментов расслаивается на простейшие фигуры.
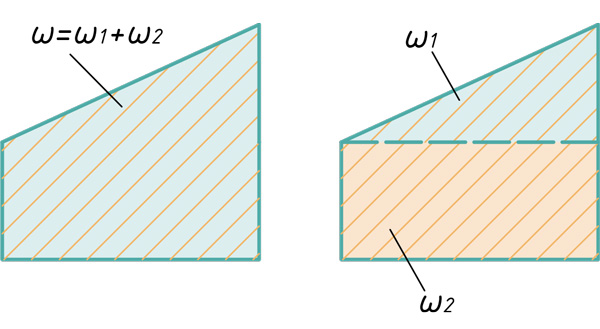
Любой самый сложный участок эпюры можно расслоить на три простейшие фигуры: прямоугольник, прямоугольный треугольник и параболический сегмент.
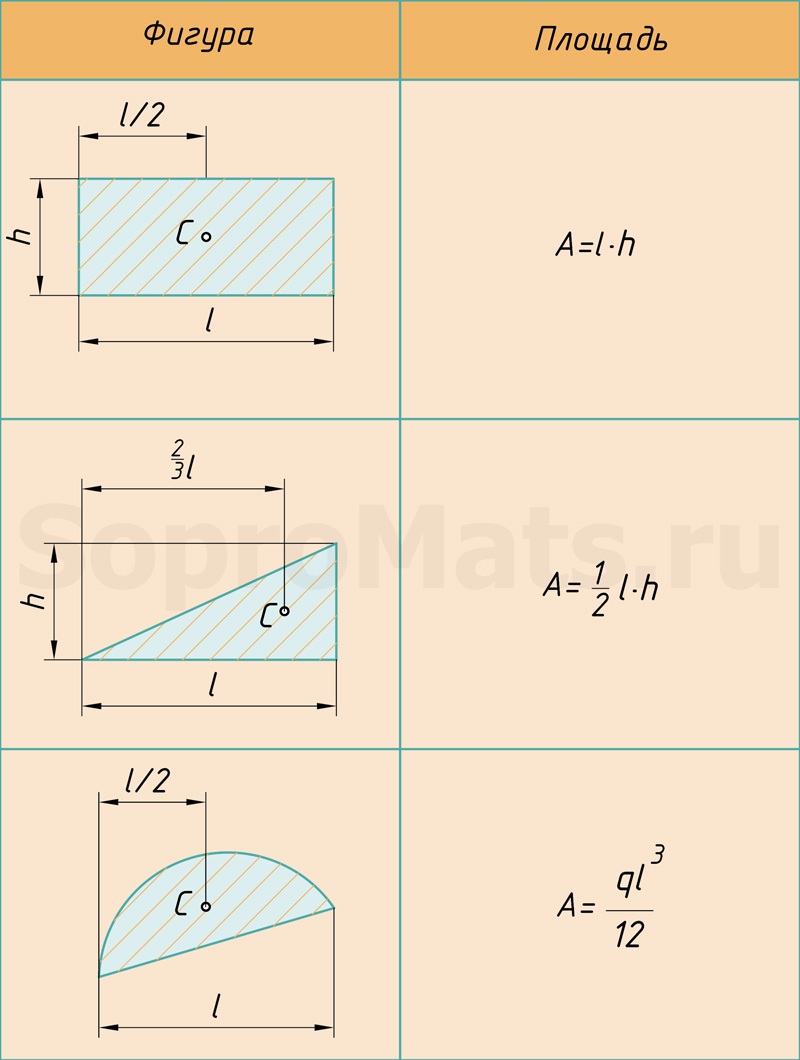
Поэтому именно с этими фигурами будем дальше работать. Напомню, как вычислить их площадь и где у них находится центр тяжести. Все формулы и размеры оформил в виде таблицы:
Перемножение простейших эпюр по Верещагину
В этом блоке статьи покажу простейшие случаи перемножения эпюр по Верещагину.
Прямоугольник на прямоугольник
Прямоугольник на треугольник
Треугольник на прямоугольник
Параболический сегмент на прямоугольник
Параболический сегмент на треугольник
Расслоение эпюр на простые фигуры
В этом блоке статьи покажу способы расслоения эпюр на простые фигуры, для дальнейшего их перемножения по правилу Верещагина.
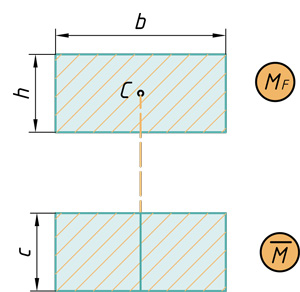
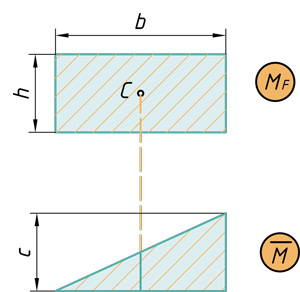
Прямоугольник и треугольник
Два треугольника
Два треугольника и параболический сегмент
Треугольник, прямоугольник и параболический сегмент
Пример определения перемещений: прогибов и углов поворотов по Верещагину
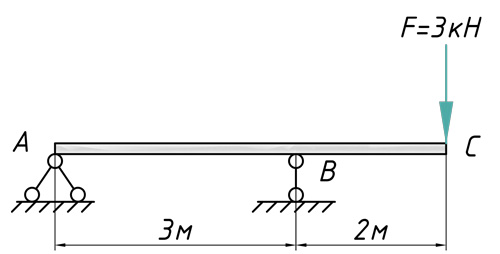
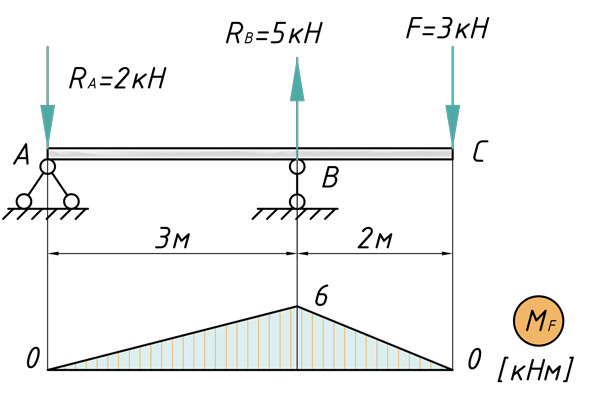
Теперь предлагаю рассмотреть конкретный пример с расчетом перемещений поперечных сечений: их прогибов и углов поворотов. Возьмем стальную балку, которая загружена всевозможными типами нагрузок и определим прогиб сечения C, а также угол поворота сечения A.
Построение эпюры изгибающих моментов
В первую очередь рассчитываем и строим эпюру изгибающих моментов:
Построение единичных эпюр
Теперь для каждого искомого перемещения необходимо приложить единичную нагрузку в ту точку, где это перемещение определяется и построить единичные эпюры:
- для прогибов прикладываются единичные силы.
- для углов поворотов прикладываются единичные моменты.
Все прикладываемые нагрузки являются безразмерными величинами. Причем, направление этих нагрузок неважно! Расчет покажет верное направление перемещений.
Например, после расчета величина прогиба получилась положительной, это значит, что направление перемещения сечения совпадает с направлением ранее прикладываемой единичной силы. То же самое касается и углов поворотов.
Перемножение участков эпюры по Верещагину
После проведения всех подготовительных работ: построения эпюры изгибающих моментов, расслоения ее на элементарные фигуры и построения единичных эпюр от нагрузок, приложенных в местах и направлении искомых перемещений, можно переходить непосредственно к перемножению соответствующих эпюр.
Как уже было написано выше, линейные эпюры можно перемножать в любом порядке, то есть брать площадь любой эпюры: основной или единичной, и умножать на ординату другой. Но обычно, чтобы не путаться в расчетах, площади берут основной эпюры изгибающих моментов, в этом уроке будем придерживаться этого же правила.
Определение прогиба сечения С
Перемножаем соответствующие эпюры слева направо и вычисляем прогиб сечения C по методу Мора — Верещагина:
\[ < V >_< C >=\frac < 1 >< E< I >_ < x >> (\frac < 1 > < 2 >\cdot 6\cdot 3\cdot \frac < 2 > < 3 >\cdot 2+\frac < 1 > < 2 >\cdot 6\cdot 2\cdot \frac < 2 > < 3 >\cdot 2)=\frac < 20кН< м >^ < 3 >>< E< I >_ < x >> \]
Представим, что рассчитываемая балка имеет поперечное сечение в виде двутавра №24 по ГОСТ 8239-89, тогда прогиб балки будет равен:
Определение угла поворота сечения С
Перемножаем соответствующие эпюры слева направо и вычисляем угол поворота сечения C по правилу Мора — Верещагина:
Для закрепления пройденного материала рекомендую изучить примеры, где рассмотрены различные случаи расслоения и перемножения эпюр.
Источник
1.11. Определение перемещений при изгибе по способу Верещагина
Существует несколько способов (методов) определения перемещений при изгибе: метод начальных параметров; энергетический метод; метод Мора и способ Верещагина. Графо- аналитический способ Верещагина по сути является частным случаем метода Мора при решении сравнительно простых задач, поэтому его еще называют способом Мора – Верещагина. Ввиду краткости нашего курса рассмотрим только этот способ.
Запишем формулу Верещагина
y = (1/EJ)*ωг*М1г, (1.14)
где y – перемещение в интересующем сечении;
E – модуль упругости;J –осевой момент инерции;
EJ – жесткость балки на изгиб;ωг – площадь грузовой эпюры моментов;М1г– момент, снятый с единичной эпюры под центром тяжести грузовой.
В качестве примера, определим прогиб консольной балки под действием силы, приложенной на свободном конце балки.
Построим грузовую эпюру моментов.
ωг – площадь грузовой эпюры, то есть площадь полученного треугольника.
ωг = — F* l* l/2 = — F* l 2 /2.
М1г– можно получить только с единичной эпюры.
Правило построения единичной эпюры:
- с балки убираются все внешние силы;
- в интересующем сечении прикладывают единичную силу (безразмерную) по направлению предполагаемого перемещения;
- строят эпюру от этой единичной силы.
Центр тяжести прямоугольного треугольника лежит на 2/3 с вершины. Из центра тяжести грузовой эпюры спускаемся на единичную эпюру и отмечаем М1г.Из подобия треугольников можно записать М1г/(- 1*l) = 2/3 l/ l, отсюдаМ1г= — 2/3 l. Подставим полученные результаты в формулу (1.14). y= (1/EJ)*ωг*М1г= (1/EJ)*( -F*l 2 /2)*( — 2/3 l) =F*l3/3EJ. Расчет перемещений проводится после прочностного расчета, поэтому все необходимые данные известны. Подставив численные значения параметров в полученную формулу, Вы найдете перемещение балки в мм. Рассмотрим еще одну задачу. Предположим, Вы решили из круглого стержня сделать перекладину длиной 1,5 м для занятий гимнастикой. Необходимо подобрать диаметр стержня. Кроме того, Вы хотите знать, на сколько этот стержень прогнется под вашим весом. Дано: F = 800 Н (≈ 80кг); Сталь 20Х13 (нержавейка), имеющаяσв= 647 МПа; E = 8*10 4 МПа; l = 1,5 м; a = 0,7 м; b = 0,8 м. Условия работы конструкции повышенной опасности (Вы сами крутитесь на перекладине), принимаем n = 5. Соответственно [σ] = σв/ n = 647/5 = 130 МПа. Рис.1.22Решение: Расчетная схема показана на рис.1.22. Определим реакции опор. ∑MВ = 0.RА*l–F*b= 0. RА=F*b/l= 800*0,8/1,5 = 427 Н. ∑MА = 0. RВ*l – F*a = 0. RВ = F*a/l = 800*0,7/1,5 = 373 Н. Проверка ∑FY= 0.RА +RВ–F= 427 + 373 — 800 = 0. Реакции найдены правильно. Построим эпюру изгибающих моментов (это и будет грузовая эпюра). М(z1) =RА* z1. 0 ≤z1≤ a. М(0) = 0. М(a) = RА* a = 427*0,7 = 299 Н*м. М(z2) = RА*( a + z2) – F* z2. 0 ≤z2≤b. М(0) = RА*a= 427*0,7 = 299 Н*м. М(b)=RА*( a +b) – F* b = 427*1,5 – 800* 0,8 = 0. Из условия прочности запишем Wх ≥ Мг/[σ] = 299*10 3 / 130 = 2300 мм 3 . Для круглого сечения Wх = 0,1d3, отсюда d≥3√10Wх = 3√23000 = 28,4 мм ≈ 30 мм. Определим прогиб стержня. Расчетная схема и единичная эпюра показаны на рис.1.22. Воспользовавшись принципом независимости действия сил и, соответственно, независимости перемещений, запишем y = y1+ y2y1=(1/EJ)*ωг1*М1г1= (1/EJ)* F* a 2 * b/(2*l)* 2*a* b /(3*l) = = F* a 3 * b 2 /(3* EJ* l 2 ) = 800*700 3 *800 2 /(3*8*10 4 *0,05*30 4 *1500 2 ) = 8 мм. y2=(1/EJ)*ωг2*М1г2= (1/EJ)* F* a* b 2 /(2*l)* 2*a* b /(3*l) = F* a 2 * b 3 /(3* EJ* l 2 ) = 800*700 2 *800 3 /(3*8*10 4 *0,05*30 4 *1500 2 ) = 9 мм. y = y1+ y2= 8 + 9 = 17 мм. При более сложных расчетных схемах эпюры моментов приходится разделять на большее количество частей или аппроксимировать треугольниками и прямоугольниками. В результате решение сводится к сумме решений, аналогичных приведенным выше.
Источник
2. Правило Мора-Верещагина (графический способ вычисления интеграла Мора)
Кроме метода начальных параметров существует эффективный универсальный метод определения перемещений в балках, рамах и упругих конструкциях произвольной конфигурации – метод Мора. Упругое перемещение 


, (1.3)
где 

Упрощение операций интегрирования возможно для конструкций с прямолинейной осью постоянной жесткости и основано на том, что эпюры от единичных усилий на прямолинейных участках оказываются линейными. Рассматривая эту процедуру применительно к участку балки, преобразуем интеграл Мора с учетом этой особенности. На рис. 1.3 сверху показан участок балки с эпюрой 



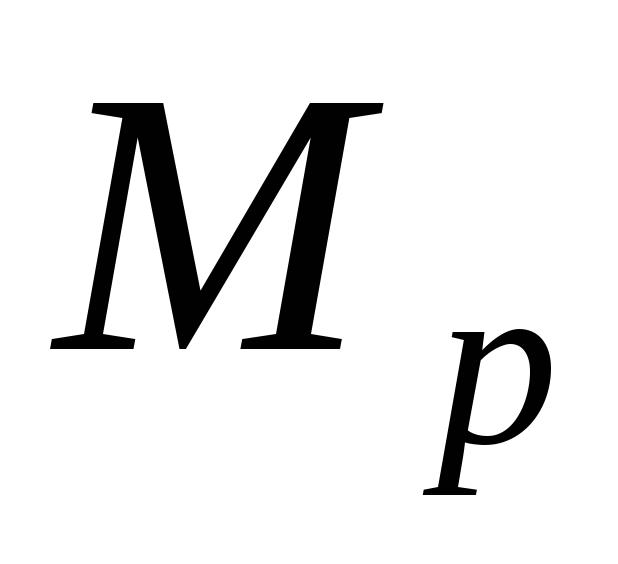


. (1.4)
Если балка имеет несколько участков по длине, формула Верещагина будет иметь вид
, (1.5)
где 
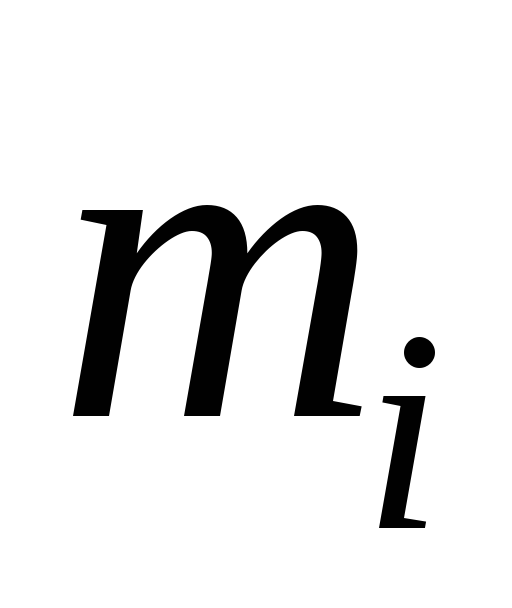

При пользовании этой формулой надо уметь вычислять площади и координаты центров тяжести основных фигур: прямоугольника, прямолинейного треугольника и криволинейного треугольника. Минимально необходимые справочные данные приведены в табл. 1.1. Процедуру графического вычисления называют «перемножением» эпюр.
Эпюры 
эпюры ,
тяжести
Эпюры 
эпюры ,
тяжести
Примечания: 1. Все кривые в табл. 1.1 – квадратные параболы. 2. При «перемножении» эпюр одного знака их произведение положительно. 3. При «перемножении» эпюр разных знаков их произведение отрицательно.
В случае, если эпюра тоже линейная, операция перемножения обладает свойством коммутативности: безразлично, умножается ли площадь грузовой эпюры на ординату единичной или площадь единичной на ординату грузовой.
Рассмотрим на примере расчетной схемы, показанной на рис. 1.4, порядок решения задач при определении перемещения с помощью правила Мора-Верещагина. Определим прогиб в точке .
Чтобы построить эпюры 


В соответствии с формулой (1.5)
.
Источник