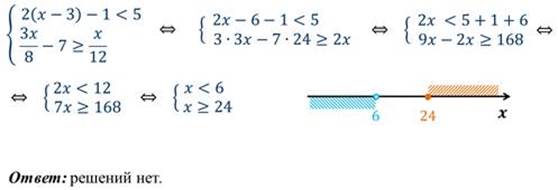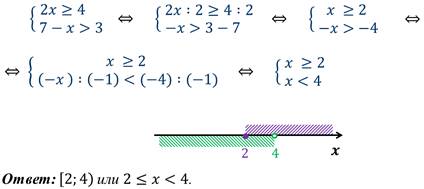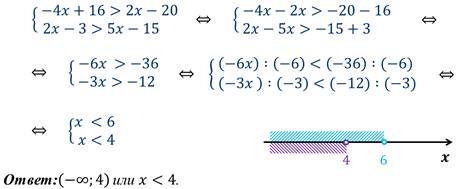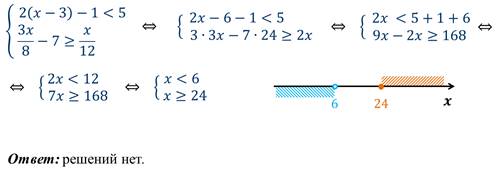Нужно заполнить водой пустой бассейн вместимостью 3000л

Тема урока «Решение систем неравенств с одной переменной»

Изучите § 35 (стр. 194-197) и видеоматериал по ссылке:

В этом уроке мы познакомимся с понятием системы неравенств с одной переменной и ее решением. Сформируем умения решать системы неравенств. Научимся записывать решение систем неравенств, используя геометрическую интерпретацию, в виде числовых промежутков.

Давайте решим задачу: нужно заполнить водой пустой бассейн вместимостью 3000 л. Сколько литров воды в час нужно наливать в бассейн, чтобы через 2 часа он был наполнен более половины и чтобы через 3 часа бассейн не переполнился?

Когда необходимо найти такие значения х, при которых одновременно верны два неравенства с одной переменной, их записывают совместно и говорят, что они образуют систему неравенств.

Фигурная скобка показывает, что нужно найти такие значения х, при которых оба неравенства системы обращаются в верные числовые неравенства.

Система, которую мы записали для решения задачи – это пример системы линейных неравенств с одной переменной.

Решением системы неравенств с одной переменной называется значение переменной, при котором верно каждое из неравенств системы.

В виде системы может быть записано и любое двойное неравенство.

Решить систему неравенств – значит найти все её решения или доказать, что решений нет.

Рассмотрим несколько примеров решения систем линейных неравенств с одной переменной.

Пример 1: решим систему неравенств.

Пример 2: решим систему неравенств.

Пример 3: решим систему неравенств.

Пример 4: решим двойное неравенство.

Запишем алгоритм решения систем линейных неравенств с одной переменной.

Для того чтобы решить систему неравенств, надо:

1. Решить каждое из неравенств системы.

2. Изобразить множество решений каждого неравенства на координатной прямой.

3. Найти пересечение промежутков (если оно есть) и записать в виде обозначения промежутка или в виде неравенства, задающего этот промежуток, или сделать вывод об отсутствии решения системы.

Домашнее задание

Изучить § 35 (стр. 194-197), выучить алгоритм решения систем линейных неравенств с одной переменной, решить №876, №878.

Выполненное домашнее задание прислать до 10.04.2020 на почту:

Источник

Материалы к уроку: Веселая математика: Неравенства

специалист в области арт-терапии

Описание презентации по отдельным слайдам:

Закончи предложения: — Неравенства вида aх>b или аx (линейными неравенствами с одной переменной). — Множество всех чисел, удовлетворяющих условию a или 3 слайд

Цели урока: Задачи урока: Обобщить знания по теме. Учится применять полученные знания на практике. Сознательно относиться к учёбе. Сотрудничать с учителем и со сверстниками. 1.Познакомится с понятием системы неравенств и её решением. 2.Сформировать умение решать системы неравенства. 3.Научиться записывать решение системы неравенства в виде числовых промежутков.

физминутка Шишку в руки дружно взяли И в ладошках покатали, Покрутили, повертели Вновь работать захотели.

Решим задачку: нужно заполнить водой пустой бассейн вместимостью 3000 л. Сколько литров воды в час нужно наливать в бассейн, чтобы через 2 часа он был наполнен более половины и чтобы через 3 часа бассейн не переполнился? Решение:

Когда необходимо найти такие значения х, при которых одновременно верны два неравенства с одной переменной, их записывают совместно и говорят, что они образуют систему неравенств. Фигурная скобка показывает, что нужно найти такие значения х, при которых оба неравенства системы обращаются в верные числовые неравенства. Система, которую мы записали для решения задачи – это пример системы линейных неравенств с одной переменной.

Решением системы неравенств с одной переменной называется значение переменной, при котором верно каждое из неравенств системы. Решить систему неравенств – значит найти все её решения или доказать, что решений нет.

В виде системы может быть записано и любое двойное неравенство. Давайте попробуем сделать это самостоятельно…

Зрительная гимнастика Рисуй глазами треугольник Рисуй глазами треугольник. Теперь его переверни Вершиной вниз. И вновь глазами ты по периметру веди. Рисуй восьмерку вертикально. Ты головою не крути, А лишь глазами осторожно ты вдоль по линиям води. И на бочок ее клади

Составим алгоритм решений системы линейных уравнений с одной переменной: Записать систему неравенств; Решить каждое из неравенств; Изобразим множество решений на координатной прямой; Найдём пересечения промежутков, если такие имеются.

Итог: Что образует систему неравенств? Как называется значение переменной при котором верно каждое из неравенств? 3. Что значит решить систему неравенств?

— Неравенства вида aх>b или аx (линейными неравенствами с одной переменной).

Номер материала: ДБ-1508711

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

В России создадут «белый интернет» для школьников

Время чтения: 1 минута

Итальянский учитель дал детям задание на лето и прославился

Время чтения: 4 минуты

Треть россиян за полгода не прочли ни одной книги

Время чтения: 1 минута

Рособрнадзор: почти половина учителей не дотягивает до базового уровня подготовки

Время чтения: 2 минуты

МГУ вновь занял первое место в рейтинге лучших вузов России

Время чтения: 1 минута

Самарских студентов будет учить робот

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Решение систем неравенств с одной переменной

Урок 33. Алгебра 8 класс ФГОС

Конспект урока «Решение систем неравенств с одной переменной»

Давайте решим задачу: нужно заполнить водой пустой бассейн вместимостью 3000 л. Сколько литров воды в час нужно наливать в бассейн, чтобы через 2 часа он был наполнен более половины и чтобы через 3 часа бассейн не переполнился?

Когда необходимо найти такие значения х, при которых одновременно верны два неравенства с одной переменной, их записывают совместно и говорят, что они образуют систему неравенств.

Фигурная скобка показывает, что нужно найти такие значения х, при которых оба неравенства системы обращаются в верные числовые неравенства.

Система, которую мы записали для решения задачи – это пример системы линейных неравенств с одной переменной.

Решением системы неравенств с одной переменной называется значение переменной, при котором верно каждое из неравенств системы.

В виде системы может быть записано и любое двойное неравенство.

Решить систему неравенств – значит найти все её решения или доказать, что решений нет.

Рассмотрим несколько примеров решения систем линейных неравенств с одной переменной.

Пример 1: решим систему неравенств.

Пример 2: решим систему неравенств.

Пример 3: решим систему неравенств.

Пример 4: решим двойное неравенство.

Запишем алгоритм решения систем линейных неравенств с одной переменной.

Для того чтобы решить систему неравенств, надо:

1. Решить каждое из неравенств системы.

2. Изобразить множество решений каждого неравенства на координатной прямой.

3. Найти пересечение промежутков (если оно есть) и записать в виде обозначения промежутка или в виде неравенства, задающего этот промежуток, или сделать вывод об отсутствии решения системы.

Источник

Решение систем неравенств с одной переменной

Урок 33. Алгебра 8 класс ФГОС

Конспект урока «Решение систем неравенств с одной переменной»

Давайте решим задачу: нужно заполнить водой пустой бассейн вместимостью 3000 л. Сколько литров воды в час нужно наливать в бассейн, чтобы через 2 часа он был наполнен более половины и чтобы через 3 часа бассейн не переполнился?

Когда необходимо найти такие значения х, при которых одновременно верны два неравенства с одной переменной, их записывают совместно и говорят, что они образуют систему неравенств.

Фигурная скобка показывает, что нужно найти такие значения х, при которых оба неравенства системы обращаются в верные числовые неравенства.

Система, которую мы записали для решения задачи – это пример системы линейных неравенств с одной переменной.

Решением системы неравенств с одной переменной называется значение переменной, при котором верно каждое из неравенств системы.

В виде системы может быть записано и любое двойное неравенство.

Решить систему неравенств – значит найти все её решения или доказать, что решений нет.

Рассмотрим несколько примеров решения систем линейных неравенств с одной переменной.

Пример 1: решим систему неравенств.

Пример 2: решим систему неравенств.

Пример 3: решим систему неравенств.

Пример 4: решим двойное неравенство.

Запишем алгоритм решения систем линейных неравенств с одной переменной.

Для того чтобы решить систему неравенств, надо:

1. Решить каждое из неравенств системы.

2. Изобразить множество решений каждого неравенства на координатной прямой.

3. Найти пересечение промежутков (если оно есть) и записать в виде обозначения промежутка или в виде неравенства, задающего этот промежуток, или сделать вывод об отсутствии решения системы.

Источник