Над центром круглого бассейна радиусом 5 м залит до краев водой висит лампа

Над центром круглого бассейна радиусом 5 м, залитого до краев водой, висит лампа

Условие задачи:

Над центром круглого бассейна радиусом 5 м, залитого до краев водой, висит лампа. Максимальное расстояние, на которое может отойти человек ростом 1,8 м от края бассейна, чтобы видеть изображение лампы в воде, равно 3 м. На каком расстоянии от своих глаз наблюдатель видит изображение лампы?

Задача №10.1.6 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Решение задачи:

Для решения задачи нужно сделать рисунок. Условно покажем человека AB ростом \(h\), стоящего на расстоянии \(l\) от края бассейна радиусом \(r\). Через голову человека B и край бассейна C проведем некоторый луч – это крайнее направление лучей, при котором человек ещё видит изображение лампы в воде. От центра бассейна проведем перпендикуляр до пересечения с лучом, в месте пересечения должно находится изображение лампы O’ в воде. Изображение лампы находится на некоторой глубине \(H\), сама же лампа O находится на такой же высоте над центром бассейна (правило построения изображения в воде такое же, как правило построения изображения в зеркале).

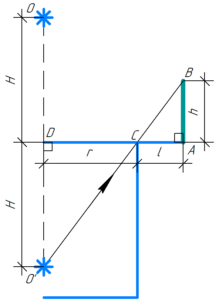
Из рисунка прекрасно видно, что искомое расстояние \(L\) это сумма длин отрезков BC и CO’, которые легко можно определить, воспользовавшись теоремой Пифагора. Поэтому:

Неизвестную величину \(H\) можно определить благодаря подобию треугольников ABC и CDO’. Тогда:

Подставим полученное выражение (2) в формулу (1):

Вынесем \(r^2\) из второго корня:

Приведем во втором корне под общий знаменатель:

Вынесем \(l^2\) из знаменателя дроби во втором корне:

Численный ответ равен:

Ответ: 9,33 м.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Источник

Презентация по физике на тему «Решение задач по оптике»

специалист в области арт-терапии

Описание презентации по отдельным слайдам:

Разбор решения задач ЕГЭ (Геометрическая оптика) Подготовлена: учителем физики ГКОУ РО лицея-интерната «Педагогический» г. Таганрога Пивень Ю.А.

H h l1 x Дано h=1 м l1 = 0,8 м d = 1 м l2 = 1,25 м Найти H — ? Вертикальный колышек высотой h = 1 м, поставленный вблизи уличного фонаря, отбрасывает тень длиной l1 = 0,8 м. Если перенести колышек на d = 1 м дальше от фонаря (в той же плоскости), то он отбрасывает тень длиной l2 = 1,25 м. На какой высоте H подвешен фонарь?

H D1 C1 A B1 l2 x Дано h=1 м l1 = 0,8 м d = 1 м l2 = 1,25 м Найти H — ? О Передвинем предмет d

Получили два уравнения, с двумя неизвестными Дано h=1 м l1 = 0,8 м d = 1 м l2 = 1,25 м Найти H — ?

Круглый бассейн радиусом R = 5 м залит до краев водой. Над центром бассейна на высоте Н = 3 м от поверхности воды висит лампа. На какое расстояние l от края бассейна может отойти человек, рост которого h = 1,8 м, чтобы все еще видеть отражение лампы в воде? Дано R=5 м H = 3 м h = 1,8 м Найти L — ? H h R L

Равнобедренный прямоугольный треугольник ABC расположен перед тонкой собирающей линзой оптической силой 2,5 дптр так, что его катет AC лежит на главной оптической оси линзы (см. рисунок). Вершина прямого угла C лежит дальше от центра линзы, чем вершина острого угла A, расстояние от центра линзы до точки A равно удвоенному фокусному расстоянию линзы, AC = 4 см. Постройте изображение треугольника и найдите площадь получившейся фигуры. F 2F C A B A’ C’ B’ d f

F 2F C A B A’ C’ B’ d f Формула площади треугольника ? Формула площади прямоугольного треугольника ?

F 2F C A B A’ C’ B’ d f Назовите катеты для решения нашей задачи: Катет A’C’ найдем из формулы увеличения линзы и формулы тонкой линзы.

F 2F C A B A’ C’ B’ d f Назовите катеты для решения нашей задачи: Катет A’C’ найдем из формулы увеличения линзы и формулы тонкой линзы.

F 2F C A B A’ C’ B’ d f Из чертежа видно, что изображение треугольника не является равнобедренным треугольником Как найти C’B’? 2F

Список используемых источников: Сайт www.reshuege.ru

Номер материала: ДВ-065083

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Подарочные сертификаты

Более 80% студентов при выборе работы на первое место ставят зарплату

Время чтения: 1 минута

Китайский университет зачислил на факультет информатики искусственный интеллект

Время чтения: 1 минута

Минздрав разрешит исследования «Спутника V» на детях с 12 лет

Время чтения: 1 минута

Каждый третий школьник отстает в учебе

Время чтения: 3 минуты

Итальянский учитель дал детям задание на лето и прославился

Время чтения: 4 минуты

Самарских студентов будет учить робот

Время чтения: 1 минута

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Задание EF19015

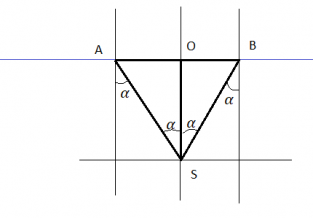
На дне бассейна с водой находится небольшая лампочка. На поверхности воды плавает круглый плот – так, что центр плота находится точно над лампочкой. Определите глубину бассейна Н, если минимальный радиус плота, при котором свет от лампочки не выходит из воды, R = 2,4 м. Сделайте рисунок, поясняющий решение. Толщиной плота пренебречь. Показатель преломления воды n = 4/3.

Решение

Алгоритм решения

Решение

Запишем исходные данные:

Выполним рисунок. Проведем перпендикуляры к поверхности: перпендикуляр от точечного источника света, а также нормали, проведенные через края плота.

Чтобы свет лампочки не выходил из воды, лучи света от лампочки, направленные к границе между краем плота и поверхностью воды, должны полностью отражаться. Это возможно только при выполнении следующего условия:

Поскольку вершина S треугольника ABS лежит строго под центром круглого плота, этот треугольник является равнобедренным. Причем перпендикуляр, восстановленный к основанию треугольника AB — SO — делит это основание на 2 равные стороны. Одновременно он делит угол S этого треугольника на 2 равные части, так как он является одновременно перпендикуляром, медианой и биссектрисой.

Пусть α — угол падения луча. Тогда угол OSB будет равен этому углу как накрест лежащие углы.

Треугольник OSB — прямоугольный. Причем искомая величина — глубина бассейна — является одним из его катетов. Из курса геометрии известно, что катет равен произведения второго катета на котангенс прилежащего угла. Второй катет в нашем случае — радиус круглого плота. Прилежащий угол равен углу падения. Следовательно:

Котангенс угла определяется как отношение косинуса этого угла к его синусу:

cot . α = cos . α sin . α . .

Косинус угла можем выразить из основного тригонометрического тождества:

sin 2 . α + cos 2 . α = 1

cos . α = √ 1 − sin 2 . α

Отсюда котангенс равен:

cot . α = √ 1 − sin 2 . α sin . α . .

Тогда глубина бассейна:

H = R cot . α = R √ 1 − sin 2 . α sin . α . .

Из закона полного отражения вспомним, что синус угла падения есть величина, обратная показателю преломления воды. Тогда эта формула примет вид:

H = R √ 1 − ( 1 n . . ) 2 1 n . . . . = R n √ 1 − 1 n 2 . .

Подставим известные данные и получим:

H = 2 , 4 · 4 3 . .   .  .  ⎷ 1 − 1 ( 4 3 . . ) 2 . . = 3 , 2 √ 1 − 9 16 . . = 3 , 2 √ 7 4 . . ≈ 0 , 8 · 2 , 65 = 2 , 12 ⎛ ⎜ . ⎜ ⎝ м ⎞ ⎟ . ⎟ ⎠

Источник

Над центром круглого бассейна радиусом 5 м залит до краев водой висит лампа

Бассейн глубиной 3 м заполнен водой, относительный показатель преломления на границе воздух — вода 1,33. Каков радиус светового круга на поверхности воды от электрической лампы на дне бассейна?

Рассмотрим ход лучей, исходящих из точки А на дне бассейна. Вертикальный луч АВ не изменяет своего направления после прохождения границы раздела, все остальные лучи испытывают преломление или отражаются от границы раздела.

Полное внутреннее отражение происходит начиная с такого значения угла падения при котором угол преломления равен Следовательно, предельное значение угла при котором свет выходит из воды, определяется условием

Из треугольника АВС найдем радиус светового круга ВС:

Источник

Оптика — Урок 3 — Часть С (Высокий уровень) — Сборник задач

409. Расстояние между предметом и экраном L = 0,75 м. Линза, помещенная между ними, дает четкое изображение при двух ее положениях: один раз — уменьшенное, другой раз — увеличенное. Увеличенное изображение предмета больше самого предмета в Г = 2 раза. Чему равна оптическая сила линзы?

410. Плоское зеркало, расположенное в вертикальной плоскости, может вращаться вокруг горизонтальной оси. На расстоянии R от оси находится светящаяся точка А. Какое расстояние будет между изображением точки и изображением, которое образуется после поворота зеркала на угол α?

411. На поверхности воды плавает надувной плот шириной 4 м и длиной 6 м. Небо затянуто сплошным облачным покровом, полностью рассеивающим солнечный свет. На какой максимальной глубине под плотом должна находиться маленькая рыбка, чтобы её не могли увидеть плавающие вокруг плота хищники? Глубиной погружения плота, рассеиванием света водой и его отражением от дна водоема пренебречь. Показатель преломления воды относительно воздуха принять равным 4/3.

412. Фокусное расстояние собирающей линзы F = 5 см. Точечный источник света находится на оси линзы на расстоянии d = 6 см от нее. Линзу разрезали по диаметру на две равные части, которые раздвинули на расстояние h = 1 см симметрично относительно оптической оси. Найдите расстояние Н между двумя изображениями точки.

413. Линза, фокусное расстояние которой 20 см, дает на экране изображение предмета с четырехкратным увеличением. Экран подвинули к линзе вдоль ее главной оптической оси на расстояние l. Затем, чтобы изображение снова стало резким, передвинули предмет на расстояние 5 см. На сколько см передвинули экран относительно первоначального положения?

414. Предмет в виде отрезка длиной 6 см расположен вдоль главной оптической оси собирающей линзы с фокусным расстоянием 10 см. Середина отрезка расположена на расстоянии 15 см от линзы. Определите продольное увеличение предмета.

415. На каком расстоянии друг от друга следует расположить две линзы: рассеивающую с фокусным расстоянием —4 см и собирающую с фокусным расстоянием 9 см, чтобы пучок лучей, параллельных оптической оси линзы, пройдя через обе линзы, остался бы параллельным?

416. Круглый бассейн радиусом 5 м залит до краев водой. Над центром бассейна на высоте 3 м от поверхности воды висит лампа. На какое расстояние от края бассейна может отойти человек ростом 1,8 м, чтобы всё еще видеть отражение лампы в воде?

417. На дне водоема глубиной 2 м лежит зеркало. Луч света, пройдя через воду, отражается от зеркала и выходит из воды. Показатель преломления воды равен 1,33. Найдите расстояние между точкой входа луча в воду и точкой выхода луча из воды, если угол падения луча равен 30°.

418. Между краями двух хорошо отшлифованных тонких плоских стеклянных пластинок помещена тонкая проволочка, противоположные концы пластинок плотно прижаты друг к другу. Расстояние от проволочки до линии соприкосновения пластинок равно 20 см. На верхнюю пластинку нормально к ее поверхности падает монохроматический пучок света длиной волны 600 нм. Определите диаметр проволочки, если на 1 см длины клина умещается 10 интерференционных полос.

419. Источник монохроматического света испускает ежесекундно 2 ∙ 10 20 фотонов, вызывающих фотоэффект на металлической пластине с работой выхода электронов 1,6 ∙ 10 -19 Дж. При длительном освещении пластина заряжается до потенциала 0,9 В. Найдите мощность источника света.

Библиотека образовательных материалов для студентов, учителей, учеников и их родителей.

Наш сайт не претендует на авторство размещенных материалов. Мы только конвертируем в удобный формат материалы из сети Интернет, которые находятся в открытом доступе и присланные нашими посетителями.

Если вы являетесь обладателем авторского права на любой размещенный у нас материал и намерены удалить его или получить ссылки на место коммерческого размещения материалов, обратитесь для согласования к администратору сайта.

Разрешается копировать материалы с обязательной гипертекстовой ссылкой на сайт, будьте благодарными мы затратили много усилий чтобы привести информацию в удобный вид.

© 2014-2021 Все права на дизайн сайта принадлежат С.Є.А.

Источник