Механика грунтов круги мора

Механика грунтов. Лекция №4

Точка А прямой определяет наклон площадки к направлению главных напряжений. Треугольник О’АС прямоугольный Первое условие Так как главные напряжения взаимно перпендикулярны Из построений на рис. имеем (5) Второе условие

Выражение (5) называют условием предельного равновесия связных грунтов оно показывает соотношение между главными напряжениями при котором в данной точке массива наступает состояние предельного равновесия

Все это справедливо и для второй сопряженной площадки О’А’С Массив грунта характеризуется параметрами прочности и

Испытания по схеме трехосного сжатия Цилиндрический образец грунта 4 помещается в рабочую камеру прибора 7 заполненной водой. Образец покрывают тонкой резиновой оболочкой 6. Нормальное напряжение 1 создается через штамп 2, боковое напряжение 2 = 3 создается жидкостью рабочей камеры. Измерения давления в камере производится манометром 3, вертикальные перемещения – индикаторами 5. Для отвода воды из образца или его насыщения в процессе испытания используется система дырчатых штампов и поддона с трубками, перекрытая кранами 1. Для определения горизонтальных перемещений используется тонкая стеклянная трубка (волюмометр 8) и позволяющая измерить объем жидкости вытекающей из рабочей камеры В стабилометре можно определить как деформационные так и прочностные характеристики, причем в первом случае опыт можно проводить в условиях компрессионного испытания, так и по схеме трѐхосного сжатия. При компрессионном испытании кран волюмометра перекрывается и с помощью манометра определяется боковое давление на образец грунта.

По показаниям индикаторов определяют вертикальную деформацию 1 , по уменьшению объема жидкости в рабочей камере – боковые деформации 2 = 3 , по показаниям манометра – боковые напряжения 2 = 3 и находят значения модуля объемного сжатия К и модуля сдвига G . Прочностные характеристики грунта определяются испытанием нескольких образцов-близнецов. К каждому образцу прикладывается постоянное, но разное для каждого образца боковое давление Для каждого из этих образцов определяется значение 1 , соответствующее разрушению. Очевидно что 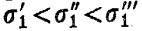Строят круги Мора Касательная к этим кругам позволяет определить параметры сопротивления грунта сдвигу и C Изложенное выше справедливо для грунтов в стабилизированном состоянии (осадка от действия сжимающего напряжения завершилась). Для нестабилизированного состояния — поровое давление

Полевые способы определения прочности грунтов Испытания шариковым штампом (Н.А.Цытович) Позволяет определить изменение прочностных свойств с течением времени

Мгновенная прочность	Длительная прочность
(мгновенные нагрузки)	(длительная устойчивость)

Зондирование основано на определении сопротивления погружению в грунт наконечника-зонда (косвенный метод) Статическое – медленное погружение в грунт зонда домкратом. Позволяет определить лобовое и боковое сопротивление грунта. В простейшем случае измеряют удельное сопротивление погружению зонда q c (МПа) и строят график. Можно определить: Модуль деформации

Характеристики	Для пылевато-глинистых
прочности
	грунтов

Динамическое – забивка или ударно-вращательное погружение. При этом определяется показатель зондирования N равный числу ударов необходимых для погружения зонда на 10 см. Зная удельную энергию установки определяют динамическое сопротивление грунта qd – позволяет судить о плотности песчаного грунта, их прочностных и деформационных показателей, а так же ориентировочное значение Е суглинков и глин.
Водопроницаемость грунтов Свойство водонасыщенного грунта под действием разности напоров пропускать через свои поры поток воды. Зависит от пористости, гранулометрического и минерального состава, градиента

напора.	В точках 1 и 2 водонасыщенного грунта, удаленных
друг от друга на расстоянии L, действуют разные
пьезометрические напоры Н 1 >H 2
Под действием разности напоров начинается
движение воды в порах грунта.
Условная скорость фильтрации v=Q/(At)
Q – расход воды
A – площадь сечения
t – время за которое измерен расход Q
Первые опыты проведены французским ученым
Дарси в 1854 году.

Скорость фильтрации прямо пропорционально разности (6) напоров ( Н=Н 1 -Н 2 ) и обратно пропорционально длине пути L i – гидравлический градиент (градиент напора), равный потере напора по длине пути фильтрации 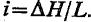k – коэффициент фильтрации , равный скорости фильтрации воды при i =1 [см/с; м/сут] всегда определяется экспериментально

1 – график песчаного грунта 2 – пылевато-глинистые грунты При небольших значениях градиента напора в пылевато-глинистых грунтах фильтрация может не возникать. Увеличение градиента приводит к постепенному развитию фильтрации. При некотором значении градиента ( i 0 ) устанавливается постоянный режим фильтрации Закон ламинарной фильтрации Дарси для пылевато-глинистых грунтов — коэффициент фильтрации определяемый в интервале зависимости м-у точками а-б i 0 — начальный градиент напора При i < i 0 фильтрации в водонасыщенном грунте не происходит

Общая задача – расчет напряженно-деформированного состояния грунтов основания Современная Механика грунтов основывается на представлениях о грунтах как о сплошной однородной деформированной среде. Другим упрощением является представление его в виде изотропного тела (свойства в любом направлении одинаковы) При проектировании наиболее ответственных сооружений используют двухкомпонентную или трехкомпонентную модель грунта Основные расчетные модели грунтов

Теория линейного	Теория	Теория предельного
деформирования	фильтрационной	напряженного
грунта	консолидации	состояния
Расчет конечных	Расчет несущей
	способности, прочности,
напряжений и		Расчет осадок во времени
	устойчивости и давления
стабилизированных осадок
	на ограждения

Модель теории линейного деформирования грунта Была обоснована трудами Н.А. Цытовича, В.А. Флорина, Н.М. Герсеванова, К. Терцаги, Н.П. Пузыревского. Распространена в инженерной практике благодаря простоте и возможности использования хорошо разработанного математического аппарата теории упругости для описания НДС (напряженно-деформированное состояние) грунтов. • Базируется на предположении, что при однократном нагружении (или разгрузке) зависимость между напряжениями и деформациями линейна. • Рассматривается общая деформация грунта без разделения на упругую и пластическую Рассматривается не вся кривая осадок Оабв, а только отрезок Оа Теория всегда требует установления предела применимости При расчете напряжений в основании и осадок грунта пределом может служить среднее давление под подошвой фундамента (Р1 на графике) Уравнения состояния модели линейного деформирования записывается в виде обобщенного закона Гука Е – модуль общей линейной деформациикоэффициент Пуассона

Модель теории фильтрационной консолидации грунта В наиболее простой постановке описывает деформирование во времени полностью водонасыщенного грунта Модель Терцаги-Герсеванова 1. Полное давление разделяется на эффективное напряжение и давление в поровой воде 2. Время и скорость деформации определяется коэффициентом фильтрации 3. Скелет грунта принимается линейно деформированным, т.е. предел применимости тот же участок оа графика.

Теория предельного равновесия Предельное состояние – это такое соотношение, между напряжениями, которое обеспечивает возможность неограниченного развития пластических деформаций (течение) грунта, а предельное равновесие – это состояние предшествующее течению грунта Позволяет определить не только несущую способность, еѐ решение используется для расчѐтов устойчивости откосов и склонов. Но в этой теории нельзя определить деформации грунта, т.е. величина осадок остаѐтся неизвестной S 2 .

Источник

Основные уравнения теории предельного равновесия

Построение круга Мора производится в следующей последовательности. От начала координат откладываем значения σ 1 и σ 3 . Из точки В проводят окружность радиусомт R . Любая точка E на окружности характеризует напряженное состояние грунта в плоскости, проходящей через рассматриваемую точку. Угол наклона α линии ЕА — это угол наклона рассматриваемой площадки к главной. Центральный угол наклона отрезка EB равен 2α. Нормальные напряжения по этой площадке а представляются по горизонтальной оси отрезком ОЕ’, касательные τ — перпендикулярным отрезком ЕЕ’ .

Значения σ и τ могут быть определены через σ 1 и σ 3 по формулам (8.1) и (8.2).

Максимальные и минимальные касательные напряжения соответствуют sin 2α = 1 и sin 2α = -1, т.е. углам 2α=π/2 или 3π/2 (α=45° или 135°).

Полное результирующее напряжение на рассматриваемой площадке

Угол отклонения σ n от нормали к площадке

Значение угла θ при изменении угла α от 0 до 90° сначала возрастает от нуля до некоторого θ max , а затем убывает до нуля.

Угол θ максимален, когда линия ОE станет касательной к кругу напряжений. Из треугольника ОBЕ :

Максимальное отклонение полного (результирующего) напряжения на угол θmax нормали к площадке имеет место при:

Следовательно, отклонения площадки скольжения от направления наибольшего главного напряжения σ 1

Таким образом, в предельном состоянии в каждой точке грунта имеются две сопряженные площадки скольжения, наклоненные под углом 45°- φ/2 к линии действия максимального и 45° + φ/2 — минимального главного напряжения ( рис. 8.3 ).

Рис. 8.3. Ориентация площадок скольжения относительно главных напряжений: 1, 2 — площадки скольжения

Для сыпучих грунтов во всех случаях θ max не может быть больше угла внутреннего трения φ. А разрушение сыпучих грунтов наступает, когда угол отклонения полного(результирующего) напряжения равен углу внутреннего трения:

Выражение (8.8) является условием прочности грунта. Тогда уравнение предельного равновесия можно записать в следующем виде:

Выражение (8.9) известно в механике грунтов как условие прочности (предельного равновесия) для песчаных (сыпучих) грунтов. После несложных тригонометрических преобразований это выражение можно записать в следующем виде:

Это выражение часто используют в теории давления грунтов на ограждения (глава 10). Для связных грунтов также можно записать условие предельного равновесия, предварительно построив круги Мора ( рис. 8.4 ) по результатам испытания в стабилометре (см. рис. 5.7).

Рис. 8.4. Круги Мора, построенные по результатам испытания образцов грунта на сжатие в стабилометре

а отрезок О’Д можно найти из выражения

Отрезок О ‘О , отсекаемый наклонной линией на оси абсцисс (см. рис. 8.4), называют давлением связности, которое можно представить в виде

Давление связности (8.14) можно условно считать начальным давлением связного грунта, которое необходимо преодолеть при испытании на сдвиг. Зная ВД (8.12) и О’Д (8.13), а также используя (8.14), найдем

Выражение (8.15), связывающее главные напряжения в момент разрушения образца с углом внутреннего трения, принято называть уравнением предельного равновесия для связных грунтов.

Уравнение (8.15) в некоторых случаях удобно использовать не в главных напряжениях, а в компонентах, записанных относительно координатных осей. Из сопротивления материалов известно, что:

Тогда, рассматривая совместно уравнения (8.15) и (8.16), можно записать уравнение предельного равновесия в следующем виде:

Аналогичным образом можно выразить и уравнение (8.9).

Источник