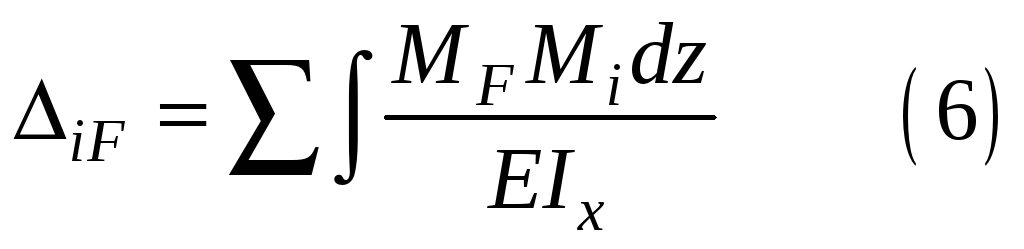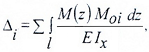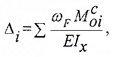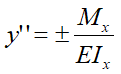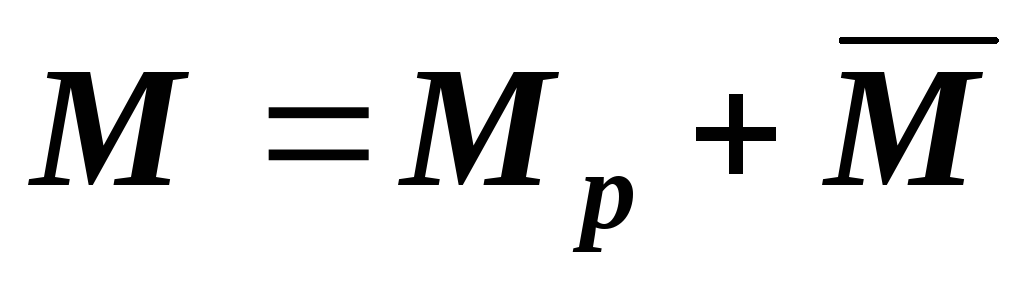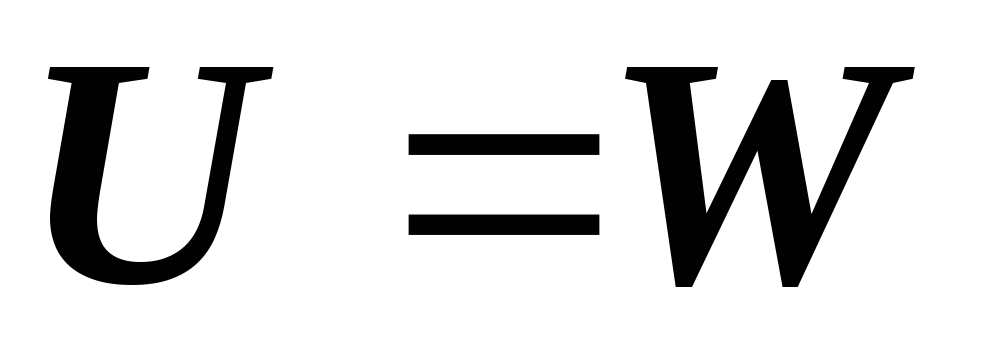Линейное перемещение интеграл мора

Метод Мора. Интеграл Мора

Теорема Кастельяно дала нам возможность определять перемещения. Эту теорему используют для отыскания перемещений в пластинках, оболочках. Однако, вычисление потенциальной энергии громоздкая процедура и мы сейчас наметим более простой и наиболее общий путь определения перемещений в стержневых системах.

П усть задана произвольная стержневая система и нам нужно определить в ней перемещение точки по направлению , вызванное всеми силами системы —

Т.к. в общем случае в системе нет силы, приложенной по направлению искомого перемещения, то воспользоваться теоремой Кастельяно нельзя. Добавим к числу прочих сил силу , приложенную к точке и действующую в направлении . Тогда внутренние силовые факторы в системе можно выразить

, где — внутренние силовые факторы в системе от действующих сил;

— внутренние силовые факторы от силы .

называемое интегралом Мора.

Для того, чтобы определить перемещение с помощью метода Мора, необходимо:

1) Определить внутренние силовые факторы в системе от заданных сил.

2) Приложить по направлению искомого перемещения единичную обобщенную силу (единичную силу для определения линейного перемещение, пару сил с моментом равным единице для определения углового перемещения и определить внутренние силовые факторы от единичной силы.

3) Подставить полученные ранее выражения в интеграл Мора и определить перемещение.

Для систем, работающих на изгиб: балок, рам, влияние нормальных сил на величину перемещения незначительно и интеграл Мора в этом случае выглядит:

Вычисление интеграла Мора по методу Верещагина

При постоянной жесткости стержня или участков стержня вычисление интеграла Мора сводится к вычислению интегралов вида:

В случае, если хотя бы один из изгибающих моментов, стоя-

щих в подинтегральном выражении, представляет собой линейную функцию координат ( в системах, состоящих из прямолинейных стержней, всегда имеет линейный вид), то возможна удобная графоаналитическая интерпретация вычисления интеграла Мора.

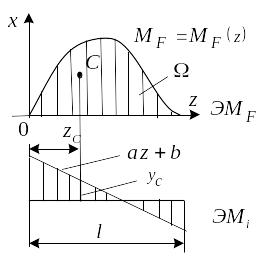
П усть эпюра очерчена по произвольному закону; — площадь этой эпюры, а — центр тяжести площади . Эпюра очерчена по линейному закону . Подставим это выражение в (1)

Для того, чтобы вычислить интеграл Мора необходимо площадь одной из эпюр умножить на ординату, взятую из другой эпюры под центром тяжести площади.

Замечание 1. Ордината берется обязательно из линейной эпюры.

Замечание 2. Эпюра, из которой берется ордината , должна быть очерчена в пределах перемножаемого участка по одному закону (это ясно из вывода).

Замечание 3. Если обе перемножаемые эпюры линейны, то “умножение” по правилу Верещагина коммутативно.

Замечание 4. Если перемножаемая площадь и ордината расположены по одну сторону от оси стержня (имеют один знак), то произ

ведение берется со знаком плюс.

Таким образом, в тех случаях, когда возможно вычисление ин

теграла Мора по правилу Верещагина перемещения можно определить следующим образом: , где индексом

пронумерованы все участки, на которые разбита система для перемножения по правилу Верещагина.

Напомним, — перемещение ищется по направлению силы .

Источник

Метод Мора. Интеграл Мора

Теорема Кастельяно дала нам возможность определять перемещения. Эту теорему используют для отыскания перемещений в пластинках, оболочках. Однако, вычисление потенциальной энергии громоздкая процедура и мы сейчас наметим более простой и наиболее общий путь определения перемещений в стержневых системах.

Пусть задана произвольная стержневая система и нам нужно определить в ней перемещение точки по направлению , вызванное всеми силами системы —

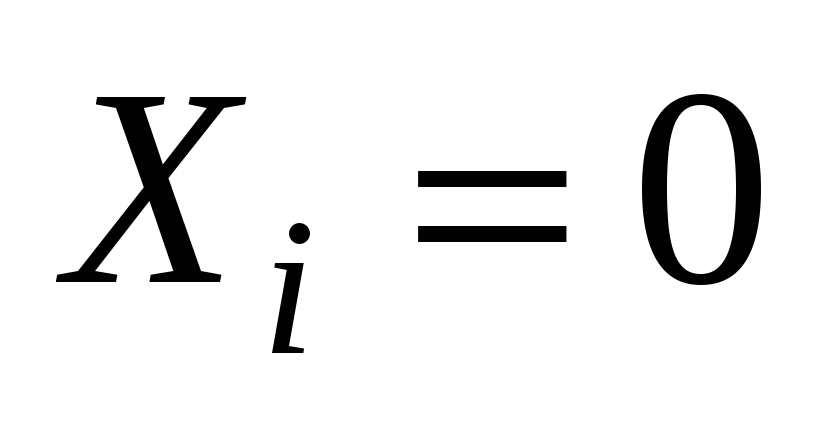
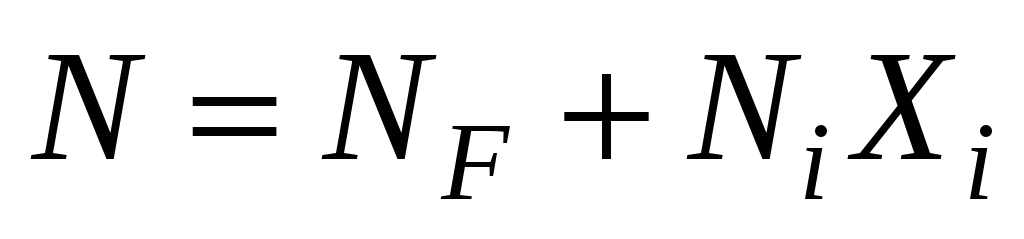
Т.к. в общем случае в системе нет силы, приложенной по направлению искомого перемещения, то воспользоваться теоремой Кастельяно нельзя. Добавим к числу прочих сил силу , приложенную к точке и действующую в направлении . Тогда внутренние силовые факторы в системе можно выразить

, где — внутренние силовые факторы в системе от действующих сил;

— внутренние силовые факторы от силы .

Внесем эти выражения в (3)

По теореме Кастельяно:

Учтя, что

получаем выражение:

называемое интегралом Мора.

Для того, чтобы определить перемещение с помощью метода Мора, необходимо:

1) Определить внутренние силовые факторы в системе от заданных сил.

2) Приложить по направлению искомого перемещения единичную обобщенную силу (единичную силу для определения линейного перемещение, пару сил с моментом равным единице для определения углового перемещения и определить внутренние силовые факторы от единичной силы.

3) Подставить полученные ранее выражения в интеграл Мора и определить перемещение.

Для систем, работающих на изгиб: балок, рам, влияние нормальных сил на величину перемещения незначительно и интеграл Мора в этом случае выглядит:

Источник

Перемещения при изгибе

Как отмечалось ранее, деформацией при изгибе является искривление продольной оси балки.

Вследствие этого искривления, точки и поперечные сечения балки получают линейные и угловые перемещения.

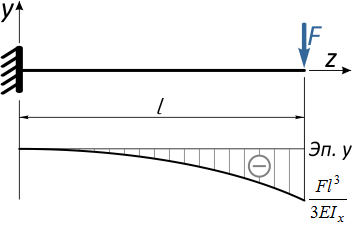
Рассмотрим на примере простой консольной балки.

Линейные перемещения

Отметим в произвольном месте балки точку K и приложим к свободному концу консоли сосредоточенную силу F.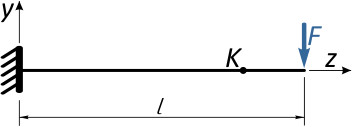

Под действием этой силы балка изогнется, и точка K переместится в новое положение K’.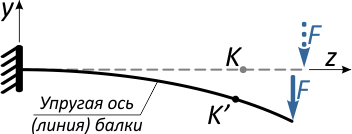

Очевидно, что перемещение точки K произойдет, не строго вертикально, поэтому разложим его на две составляющие:
вертикальное перемещение по оси y, называемое прогибом балки в т. K (y_K)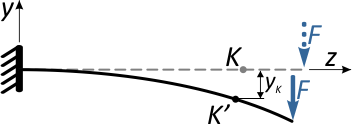

и горизонтальное (осевое) смещение точки вдоль горизонтальной оси — z_K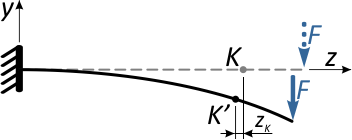

Практические расчеты показывают, что осевые смещения как правило, несоизмеримо меньше вертикальных перемещений (например, в данном случае z_K >

Интеграл Мора

Интеграл Мора относится к энергетическим методам расчета перемещений.

В отличие от МНП позволяет определять линейные и угловые перемещения для любых систем.
Подробнее >>

Способ Верещагина

Данный способ расчета перемещений представляет собой графическую интерпретацию интеграла Мора, особенностью которой является «перемножение эпюр» грузовой и единичных схем.

Подробнее >>

Метод интегрирования дифференциального уравнения упругой линии балки

Непосредственное интегрирование дифференциального уравнения упругой линии

является одним из наиболее универсальных способов расчета перемещений в балках. Может применяться без ограничений к балкам любой формы.

По результатам расчета перемещений сечений балки строится линия изогнутой оси балки (либо эпюра прогибов), с указанием числовых значений прогибов и углов наклона в характерных сечениях.

Эти вычисления и построения необходимы для проверки балок на жесткость.

Источник

4. Интеграл Мора для вычисления перемещений

Вывод формулы проводится для случая плоского изгиба, соответственно учитывается только изгибающий момент . В общем случае нагружения рассуждения аналогичны.

Задана произвольная упругая система, загруженная силами . Требуется определить перемещение произвольной точки в заданном направле-

нии .

Для вывода формулы кроме заданной рассмотрим вспомогательную единичную систему, которая представляет собой заданную упругую систему (рис. 105), к которой по направлению искомого перемещения приложена единичная сила .

Введем обозначения:

изгибающий момент —

работа внешних сил —

—

изгибающий момент —

работа силы —

—

По первому свойству упругих систем справедливы равенства:

Загрузим систему последовательно сначала единичной силой , а затем, не снимая ее, заданными силами . Из равенства энергии и работы после двух нагружений можно найти перемещение.

Работа после первого нагружения ,

после второго нагружения ,

суммарная ,

Изгибающий момент после двух нагружений

Вычисляем

Приравниваем

;

По аналогии можно вывести формулу интеграла Мора для всех случаев нагружения.

5. Частные случаи записи интеграла Мора

При расчете разных упругих систем учитывают соответствующие силовые факторы, поэтому используют разные формы записи интегралов Мора.

1. Для шарнирных стержневых систем:

2. Для плоских балок, рам и кривых брусьев

3. Для пространственных систем

6. Порядок определения перемещений по интегралу Мора

Для определения перемещений надо рассмотреть заданную и единичную системы. При определении линейного перемещения по направлению искомого перемещения прикладывается единичная сила, а при определении угла поворота сечения – единичный момент.

ычерчиваем заданную и вспомогательную системы (рис. 106), разбиваем их на участки. Границы участков в обеих системах должны совпадать. Для двух систем по участкам записываем выражения силовых факторови составляем интегралы Мора, вычислив которые, получим величину искомого перемещения.

Участок :Участок:

;

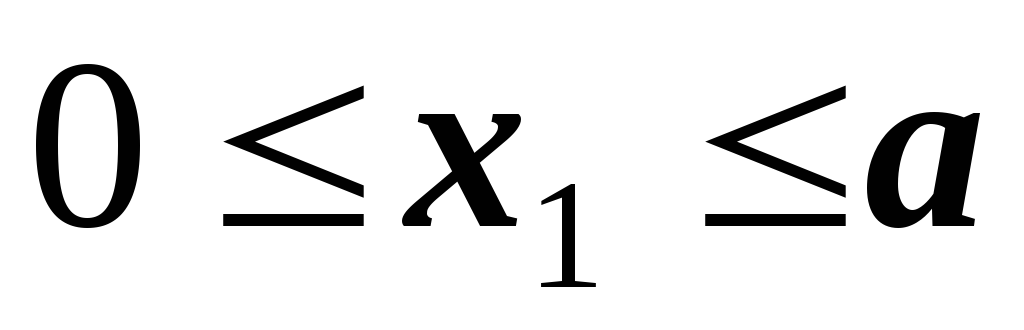
7. Правило Верещагина для вычисления интеграла Мора («перемножение» эпюр)

Интеграл Мора содержит силовые факторы от заданной нагрузки и единичных сил. Метод Верещагина основан на том, что эпюра от единичной силы и момента всегда прямолинейна, никогда не бывает параболы. Жесткость по участкам должна быть постоянной, чтобы ее можно было вынести за знак интеграла.

Вывод проводим на примере эпюр изгибающих моментов (рис. 107), но результат справедлив для любых эпюр, из которых одна линейная.

Постановка задачи: на участке балки с постоянной жесткостьюзаданы эпюрыи. Эпюраимеет произвольное очертание, эпюра— прямая линия без изломов.

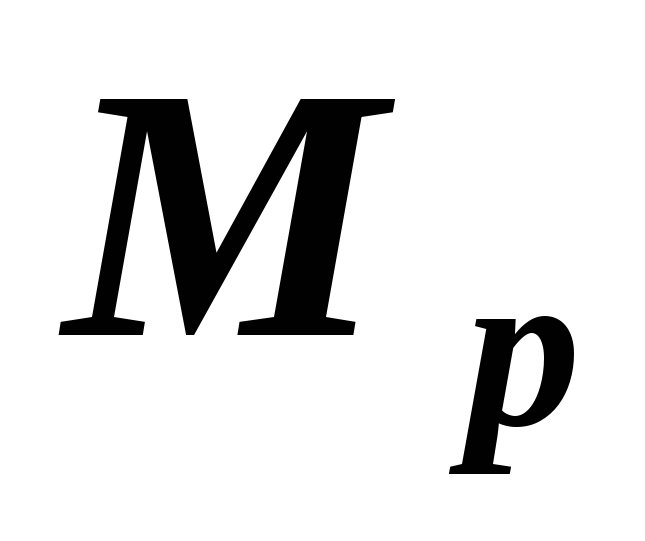
Требуется вычислить интеграл

Получено выражение, позволяющее вычислять интеграл Мора геометрически. Этот способ вычисления называется методом Верещагина.

Правило: Чтобы вычислить интеграл Мора по способу Верещагина нужно построить эпюры подинтегральных функций и, а затем площадь эпюры, обозначаемую, умножить на ординату с эпюрырасположенную под центром тяжести площади, обозначенную —.

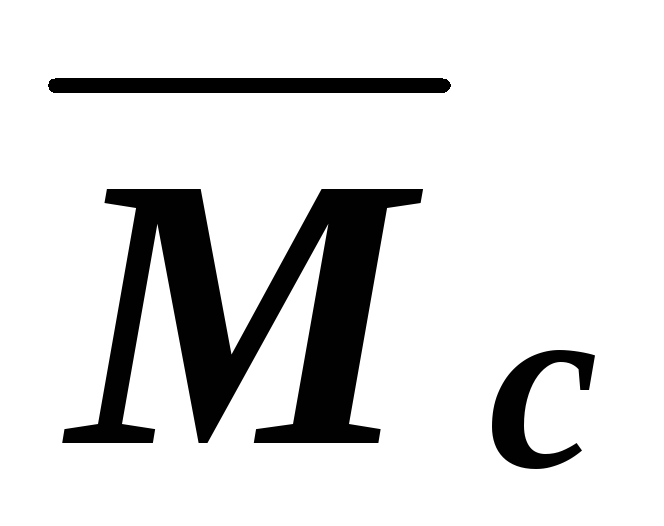
Примечание: Если обе «перемножаемые» эпюры прямолинейные, то, можно, наоборот, площадь брать с эпюры , а ординату с эпюры_.

.

Источник