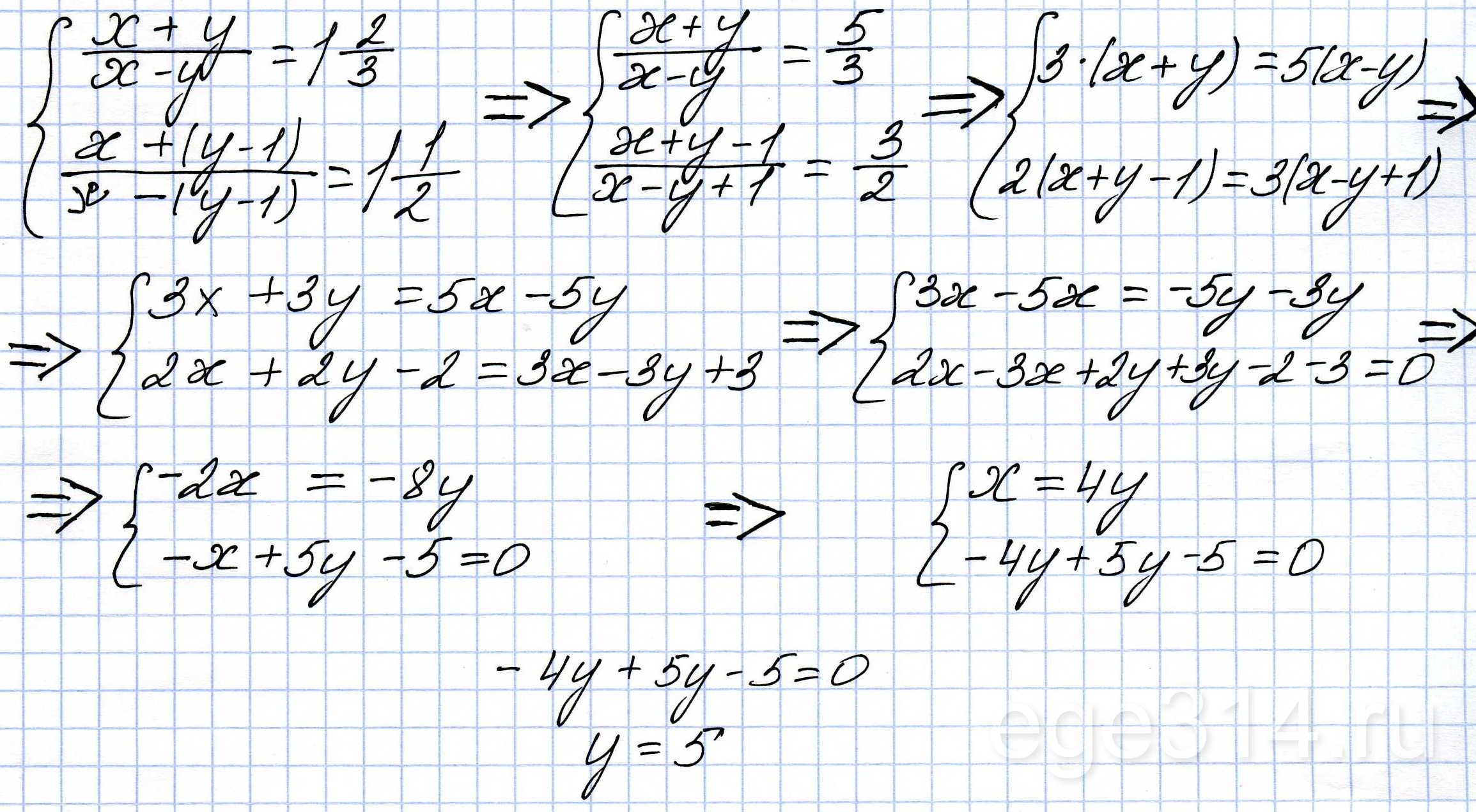Летом скорость течения равна

Помогите решить задачу, пожалуйста.

Весной катер идет против течения реки в 5/3 раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идет против течения в 3/2 раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).

Пожалуйста, напишите полное решение, можно с пояснениями. Мне понять важно, а не ответ. Спасибо.

Обозначим скорость катера — х км/ч, а скорость течения реки веской — y км/ч. Тогда летом скорость течения будет (y-1) км/ч. Весной катер по течению реки пройдет со скоростью (х+y) км/ч, а против течения — (х-y) км/ч. Скорость катера по течению реки весной будет больше скорости против течения в 5/3 раза, т.е (х-y)/(х+y)=5/3.
Летом катер по течению реки пройдет со скоростью (х+(y-1)) км/ч, а против течения — со скоростью (х-(y-1)) км/ч. Скорость катера по течению реки летом будет больше скорости против течения в 3/2 раза, т.е (х-y+1)/х+y+1)=3/2.
Получаем систему уравнений:
(х-y)/(х+y)=5/3
(х-y+1)/х+y+1)=3/2.
Выражая х через y второго уравнения и подставляя это значение в первое уравнение, найдем, что y=5.
Ответ: скорость течения реки весной равна 5 км/ч.

Даааааа Маша. ещё тот математик. ))) ну попробуй реши. то что ты написала. что у тебя получится. прям даже не знаю. ужжжжооссс.

Cогласна с предыдущим оратором => стыдно Мария выдавать неверные решения, не разобравшись, а поднахватавшись «по верхам» =>где-то и как-то. «Дык» вот => поясняю для Дарьи Подлипной.
Соотношение скоростей составлено неверно!
1)нужно соотносить скорость КАТЕРАвесной (далее=>скоростьК. в.) по течению к скорости К. в. против течения => получаем 1-ое уравнение системы: (Х+У) / (Х-У) = 5/3
2)соответственно ЛЕТОМ: СкоростьК. л. по течению к скоростиК. л. против течения
(Х+(У-1)) / (Х- (У-1) = 3/2
3)ПОЛУЧАЕМ СИСТЕМУ УРАВНЕНИЙ:
(Х+У) /(Х-У) =5/3
(Х+(У-1)) / (Х- (У-1) = 3/2
4) Выражаем из первого уравнения Х
(Х +У) х3 = 5х (Х-У)
3Х +3У = 5Х -5У
3У+5У = 5Х -3Х
8У = 2Х
Х =8У/2

5) Подставляем Х = 4У во второе уравнение:
(Х+(У-1)) / (Х- (У-1) = 3/2
(4У +(У-1)) /(4У -(У-1) =3/2
(5У-1) / (3У+1) =3/2
(5У-1)х2 = 3х (3У+1)
10У -2 = 9У +3
10У-9У = 3+2
1У =5 => У=5
Ответ: скорость течения реки весной равна 5 км/ч
Проверка
Х =4хУ =4х5=20 (км/ч — скорость Катера)
подставим в уравнение
(Х+У) / (Х-У)
(20+5) / (20-5)
25 / 15 =5/3 => что свидетельствует о верном решении задачи

Источник

Решение №529 Весной катер идёт против течения реки в 1 2/3 раза медленнее, чем по течению.

Весной катер идёт против течения реки в 1\frac раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в 1\frac раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).

Источники: Демо 2020, Демо 2019, Демо 2018, Демо 2017, Демо 2016, Демо 2015.

Весна	Лето
Скорость катера	x	x
Скорость течения	y	y – 1
Скорость катера по течению	x + y	x + (y – 1)
Скорость катера против течения	x – y	x – (y – 1)
Уравнения:	\frac=1\frac	\frac=1\frac

Получили систему уравнений, решив её найдём скорость течения весной (у):

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 4.5 / 5. Количество оценок: 101

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

Источник

Блог Олега Кривошеина

Стихи и цветы,поздравления и сценарии. Школьная математика, подготовка к ЕГЭ и ГИА,тесты, проекты,задачи и решения. Собственные произведения и фотографии моих цветов: георгины и розы.

Страницы блога

Добро пожаловать в блог! Здесь вы можете поглубже познакомиться с математикой, порешать задания ГИА и ЕГЭ, а в перерывах почитать стихи и посмотреть чудесные цветы. Удачи Вам!

четверг, 9 октября 2014 г.

Решение задач на движение

Мы продолжаем решение текстовых задач, подобных тем, что будут на ЕГЭ в 2015 году в
задании №13. В демонстрационном варианте (проекте) опубликована следующая задача:

Весной катер идёт против течения реки в 5/3 раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому катер идёт против течения в 1,5 раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).

а + х = 5/3 (а – х), умножив на 3 обе части уравнения и раскрыв скобки получаем 3а + 3х = 5 а – 5х, после приведения подобных имеем 8х = 2 а или 4х = а .

Переходим ко второй части задачи. Летом скорость течения реки на 1 км/ч меньше, то есть равна x — 1 км/ч.

Тогда скорость катера по течению равна а + х — 1 км/ч, скорость катера против течения равна а – х + 1 км/ч.

а + х – 1 = 1,5(а – х + 1), умножив на 2 обе части уравнения и раскрыв скобки получаем 2а + 2х – 2 = 3 а – 3х + 3, после приведения подобных имеем 5х = а + 5 . Из первой части мы имеем 4х = а, значит 5х = 4х + 5 и х = 5 .

2. По двум параллельным железнодорожным путям друг навстречу другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 65 км/ч и 35 км/ч. Длина пассажирского поезда равна 700 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского поезда, равно 36 секундам. Ответ дайте в метрах.

Решение. Скорость сближения поездов 65 + 35 = 100 (км/ч) = 1000/36 (м/с). Общий путь за 36 с составляет 1000/36 * 36 = 1000 (м). Тогда 1000 – 700 = 300 (м) — длина скорого поезда.

3. Поезд, двигаясь равномерно со скоростью 80 км/ч, проезжает мимо придорожного столба за 36 секунд. Найдите длину поезда в метрах.

Решение. Важно понять, что в отличие от задачи 2, придорожный столб зафиксирован. Поезд за 36 с проезжает расстояние, равное собственной длине, со скоростью 80 км/ч = 80 * 1000/3600 (м/с) = 800/36 (м/с). Длина поезда 800/36 * 36 = 800 (м).

4. Первые 190 км автомобиль ехал со скоростью 50 км/ч, следующие 180 км — со скоростью 90 км/ч, а затем 170 км — со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Решение. Напомним основную формулу: Средняя скорость = путь/время. Весь пройденный путь равен 190 + 180 + 170 = 540 км.

Источник

Как найти скорость течения реки: методика и рекомендации. Примеры решения задач

Многие люди хотя бы один раз в своей жизни путешествовали по реке на лодке, байдарке или катере. Для таких путешествий важно знать, с какой скоростью течет вода в реке, чтобы иметь возможность определить необходимое для перемещения на определенное расстояние время. В данной статье рассмотрим вопрос, как найти скорость течения реки, а также решим две физические задачи по данной теме.

Особенности течения воды в реках

Многие замечали, что одни реки текут медленно, и поверхность воды является гладкой. Обычно это крупные реки, например, Дон или Волга. Такое течение с точки зрения физики называется ламинарным, то есть слои жидкости перемещаются по прямым линиям и не смешиваются друг с другом. Более мелкие же речушки в некоторых местах буквально «бурлят». Этот тип течения характерен для рек горной местности. Он называется турбулентным. В отличие от ламинарного, здесь мелкие объемы воды перемещаются по хаотичным траекториям, на поверхности наблюдаются водовороты и пена.

Русло реки также оказывает существенное влияние на скорость течения. Так, известно, что вблизи берега и дна вода течет медленнее, чем в центральной части русла внутри ее объема. При своем движении слои воды задерживаются препятствиями, в виде неоднородностей дна и берегов, за счет трения о них. Причем каменистое дно уменьшает скорость перемещения воды сильнее, чем дно глинистое или песчаное.

Ширина русла и водоносность

Для более глубокого понимания вопроса, как найти скорость течения реки, важно знать еще один момент. Дело в том, что одна и та же река в разных местах может течь с различной скоростью. Причиной является изменение площади сечения ее русла, которое внешне связано с изменение ширины. Справедливости ради отметим, что не только изменение ширины, но и колебания в глубине влияют на быстроту течения воды (чем глубже, тем медленнее).

В виду сказанного выше, о скорости перемещения воды в реке имеет смысл говорить, если на достаточно длительном участке (километры и более) параметры ее русла колеблется незначительно, и река не имеет на этом участке притоков.

Более надежной характеристикой для любой реки является ее водоносность. Под водоносностью понимают объем воды, проходящий через вертикальное сечение русла за единицу времени. Водоносность не зависит от параметров русла, однако, она так же, как и скорость, изменится, если на рассматриваемом участке реки имеется приток.

В данной статье мы ограничимся предоставленной информацией о водоносности и перейдем к вопросу, как найти скорость течения реки.

Практический метод определения скорости воды в реке

Рассмотрим простую практическую методику, которая отвечает на вопрос, как находить скорость течения реки.

В первую очередь необходимо выбрать участок реки, где движение воды будет ламинарным, и русло не будет менять своей ширины. Затем, на берегу следует забить колышек. Он будет служить начальной отметкой. От первого колышка, используя измерительную ленту, следует отсчитать вдоль берега расстояние 10 метров, затем, забить второй колышек. Он будет конечной отметкой. Все подготовительные работы сделаны. Теперь можно переходить непосредственно к измерениям.

Как находить скорость течения реки? Для этого понадобится какой-нибудь легкий предмет, который может плавать. Например, маленькая палочка, шишка, лист бумаги, перо птицы и так далее. Предмет следует бросить в воду напротив первого колышка. При этом необходимо включить секундомер. Как только предмет, двигаясь по реке, достигнет второго колышка, секундомер нужно остановить, и зафиксировать измеренное время t.

Описанные эксперимент рекомендуется повторить несколько раз (4-5). Затем, нужно рассчитать среднее значение измеренного времени. Обозначим его t¯. Оно равно:

Здесь n — число экспериментов. Формула, как найти скорость течения, имеет вид:

Здесь L — расстояние между колышками на берегу (в данном случае оно равно 10 метрам).

Некоторые рекомендации по измерению скорости и по обработке результатов

Чтобы получить более точное значение скорости течения воды в реке, необходимо плавающий предмет бросать в воду на разные расстояния от берега. Кроме того, измерения следует проводить в безветренную погоду.

Что касается обработки результатов, то скорость в практических целях удобно представлять не в метрах в секунду, а в километрах в час. Для этого величину в м/с следует умножить на переводной коэффициент 3,6. Например, 10 м/с — это 36 км/ч.

Выше было сказано, что материал русла определяет величину уменьшения измеренной средней скорости воды в реке. Поэтому рекомендуется в случае песчано-глинистого русла умножать рассчитанное значение v на 0,9, а в случае каменистого русла — на 0,8.

Задача с рыбаком и лодкой

Разобравшись, как найти скорость течения реки, решим следующую задачу. Известно, что рыбак на лодке должен проплыть по реке 10 км. Проведя необходимые измерения, он установил, что течение в реке составляет 1 м/с. Какое время рыбаку понадобиться для того, чтобы по течению проплыть указанное расстояние, не используя при этом дополнительные средства тяги (мотор, весла).

Переводим скорость из м/с в км/ч, получаем 3,6 км/ч. Тогда искомое время будет равно:

Задача с катером

Катер движется против течения из пункта A в пункт B, расстояние между которыми составляет 5 км. Это расстояние катер прошел за 30 минут. Чему равна скорость течения реки, если известно, что скорость катера в три раза больше ее.

Обозначим скорость воды в реке x. Тогда скорость движения катера равна 3*x. Поскольку он двигался против течения, то можно записать следующее уравнение движения:

Данные из условия задачи, подставленные в полученное равенство, приводят к ответу: скорость течения равна 5 км/ч.

Источник

Летом скорость течения равна

Автор Nik2 , 9 Января 2012

19 сообщений в этой теме

Недавно просматривали 0 пользователей

Темы

Источник