Метод Мора. Интеграл Мора
Теорема Кастельяно дала нам возможность определять перемещения. Эту теорему используют для отыскания перемещений в пластинках, оболочках. Однако, вычисление потенциальной энергии громоздкая процедура и мы сейчас наметим более простой и наиболее общий путь определения перемещений в стержневых системах.
П усть задана произвольная стержневая система и нам нужно определить в ней перемещение точки по направлению , вызванное всеми силами системы —
Т.к. в общем случае в системе нет силы, приложенной по направлению искомого перемещения, то воспользоваться теоремой Кастельяно нельзя. Добавим к числу прочих сил силу , приложенную к точке и действующую в направлении . Тогда внутренние силовые факторы в системе можно выразить
, где — внутренние силовые факторы в системе от действующих сил;
— внутренние силовые факторы от силы .
называемое интегралом Мора.
Для того, чтобы определить перемещение с помощью метода Мора, необходимо:
1) Определить внутренние силовые факторы в системе от заданных сил.
2) Приложить по направлению искомого перемещения единичную обобщенную силу (единичную силу для определения линейного перемещение, пару сил с моментом равным единице для определения углового перемещения и определить внутренние силовые факторы от единичной силы.
3) Подставить полученные ранее выражения в интеграл Мора и определить перемещение.
Для систем, работающих на изгиб: балок, рам, влияние нормальных сил на величину перемещения незначительно и интеграл Мора в этом случае выглядит:
Вычисление интеграла Мора по методу Верещагина
При постоянной жесткости стержня или участков стержня вычисление интеграла Мора сводится к вычислению интегралов вида:
В случае, если хотя бы один из изгибающих моментов, стоя-
щих в подинтегральном выражении, представляет собой линейную функцию координат ( в системах, состоящих из прямолинейных стержней, всегда имеет линейный вид), то возможна удобная графоаналитическая интерпретация вычисления интеграла Мора.
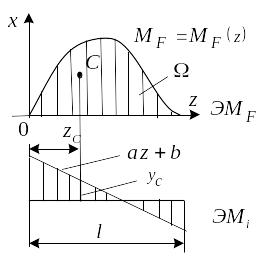
П усть эпюра очерчена по произвольному закону; — площадь этой эпюры, а — центр тяжести площади . Эпюра очерчена по линейному закону . Подставим это выражение в (1)
Для того, чтобы вычислить интеграл Мора необходимо площадь одной из эпюр умножить на ординату, взятую из другой эпюры под центром тяжести площади.
Замечание 1. Ордината берется обязательно из линейной эпюры.
Замечание 2. Эпюра, из которой берется ордината , должна быть очерчена в пределах перемножаемого участка по одному закону (это ясно из вывода).
Замечание 3. Если обе перемножаемые эпюры линейны, то “умножение” по правилу Верещагина коммутативно.
Замечание 4. Если перемножаемая площадь и ордината расположены по одну сторону от оси стержня (имеют один знак), то произ
ведение берется со знаком плюс.
Таким образом, в тех случаях, когда возможно вычисление ин
теграла Мора по правилу Верещагина перемещения можно определить следующим образом: , где индексом
пронумерованы все участки, на которые разбита система для перемножения по правилу Верещагина.
Напомним, — перемещение ищется по направлению силы .
Источник
Формула Мора. Правило Верещагина
Используется в тех случаях, когда требуется найти перемещение в
направлении не совпадающем с направлением действия сил.
Сущность интеграла Мора в следующем идеальном построении:
1. Прикладываем в интересующем направлении внешнюю силу Ф.
2. Составляем для системы выражение для потенциальной энергии
деформации U.
3. Дифференцируем выражение для U по Ф и получаем выражение для
перемещения в направлении действия Ф (то есть в интересующем
направлении)
4. В полученном выражении приравниваем Ф=0, получаем окончательное
выражение.
3.
Фиктивную силу Ф представляем в виде произведения
скалярной величины Ф на единичный силовой фактор в
соответствующем направлении.
Таким образом фиктивная сила в зависимости от
интересующего нас направления будет выражена:
N1Ф — в случае продольной силы. Определяем продольное
перемещение. N1 – единичная продольная сила
приложенная в интересующей нас точке.
Qz1Ф — в случае горизонтальной перерезывающей силы.
Определяем прогиб в горизонтальной плоскости. Qz1 –
единичная горизонтальная перерезывающая сила
приложенная в интересующей нас точке.
Q y1Ф — в случае вертикальной перерезывающей силы.
Определяем прогиб в вертикальной плоскости. Qy1 –
единичная горизонтальная перерезывающая сила
приложенная в интересующей нас точке.
4.
M K1Ф — в случае крутящего момента. Определяем угол
закручивания. MK1 – единичный крутящий момент
приложенный в интересующей нас точке.
M y1Ф — в случае момента изгибающего в горизонтальной
плоскости. Определяем угол поворота сечения в
горизонтальной плоскости. My1 – единичный
изгибающий момент в горизонтальной плоскости
приложенный в интересующей нас точке.
M z1Ф — в случае момента изгибающего в вертикальной
плоскости. Определяем угол поворота сечения в
вертикальной плоскости. Mz1 – единичный изгибающий
момент в вертикальной плоскости приложенный в
интересующей нас точке.
5.
После приложения фиктивной силы Ф значения силовых
факторов в интересующем сечении будут равны сумме
значений силовых факторов от исходной системы сил и от
силы Ф.
N N P N1Ф; Qу QуP Qу1Ф; Qz QzP Qz1Ф;
M K M KP M K1Ф; M y M yP M y1Ф; M y M zP M z1Ф.
N P , QyP , QzP , M KP , M yP , M zP — значения силовых факторов
до приложения силы Ф. (То есть в реально существующей
системе)
Подставляем в формулу для внутренней энергии:
l
U
0
l
0
N P N1Ф dx
2
2 EA
0
M KP M K1Ф dx
2
2GI K
k y QyP Qy1Ф dx
2
l
l
0
M
2GA
yP M y1Ф dx
2
2 EI y
l
0
l
0
k z QzP Qz1Ф dx
2
2GA
M zP M z1Ф 2 dx
2 EI z
6.
Дифференцируя по Ф, и принимая после этого Ф=0, находим
перемещение.
(формулы громоздкие, поэтому на примере одного
слагаемого)
l
l
2
2
2
N P N1Ф dx
N P 2 N P N1Ф N1Ф dx
Ф 0
2 EA
2 EA
Ф 0 Ф 0
Ф 0
l
2
N P dx
Ф 0 2 EA
Ф 0
l
2 N P N1Фdx
Ф 0
2 EA
Ф 0
l
2
N1Ф dx
Ф 0 2 EA
l 2 N P N1Ф
l N1Ф 2
0
dx
dx
0 Ф 2 EA Ф 0 0 Ф 2 EA
Ф 0
l
l N P N1
l 2 N1Ф
N P N1
dx
dx
dx
0 EA
Ф 0 0 2 EA
Ф 0 0 EA
Ф 0
7.
Суммируя все интегралы находим перемещение
U
N P N1
dx
Ф Ф 0 0 EA
0
l
l
l
l
M KP M K 1dx
GI K
0
0
k y QyP Q y1dx
M yP M y1dx
EI y
GA
l
k z QzPQz1dx
GA
0
l
M zP M z1dx
EI z
0
Формула носит название формула Мора, а входящие в
формулу интегралы – интегралы Мора
8.
Пример
Балка прямоугольного сечения с размерами b и 2b нагружена
моментом М. Модуль упругости материала Е, длина l заданы.
Найти прогиб концевого сечения балки С
Решение
1. Строим эпюр изгибающего момента
Мx
M
М
Mz
x
l
x
Mz=M
9.
2. Прикладываем единичную внешнюю силу в
направлении интересующего перемещения
3. Строим эпюр изгибающего момента от единичной силы
Мx
М=-x
l
4. Составляем интеграл Мора
M x
С
dx
EI z
0
x
F=1
Mz
l
x
Mz=-xF=-x
10.
11.
Интеграл Мора можно использовать для определения перемещений как
прямолинейных, так и криволинейных стержневых систем.
Поскольку интеграл Мора вычисляется по длине, для криволинейных стержней
вместо dx в подынтегральном выражении используется элемент длины дуги ds=ρdφ
где ρ — радиус кривизны стержня, который может быть постоянным, а может быть
функцией от угловой координаты φ.
ρ
2
M zP M z1
EI z d
1
dφ
φ1
φ
φ2
ds
12.
Пример:
Для кривого бруса в форме четверти круга найти горизонтальное перемещение
точки А.
Нарисуем вспомогательную единичную систему и нагрузим ее горизонтальной
единичной силой в точке А.
В полярной системе координат
положение произвольного
сечения характеризуется
радиусом-вектором ρ (в нашей
задаче ρ = Const — радиус
круга) и углом φ от произвольно
выбранной начальной точки
дуги.
13.
Изгибающий момент от внешних сил
M F F sin
Изгибающий момент от единичной силы
M1 1 1 cos 1 cos
Горизонтальное перемещение точки А
Aгор
2
M M
F 1 d
EI z
1
2
0
F sin 1 cos
F 3
d
EI z
2 EI z
2
sin ( ) ( 1 cos ( ) )
d 0.5
1
0
14.
Правило Верещагина
Правило Верещагина – графо-аналитический метод,
позволяющий упростить вычисления интегралов, входящих в
формулу Мора. Упрощение основано на том, что эпюры от
единичных силовых факторов на прямолинейных участках
оказываются линейными.
Предположим, что необходимо взять интеграл от
произведения двух функций
l
J f1 ( z ) f 2 ( z )dz
0
Пусть вторая из этих функций — линейная f 2 ( z) b kz
Тогда
l
l
J b f1 ( z )dz k zf1 ( z )dz
0
0
Первый интеграл – площадь эпюры f1(z)
l
f ( z)dz
1
0
Второй интеграл – статический момент этой эпюры
относительно оси ординат
1
15.
По свойству статического момента
l
zЦТ – координата
0 zf1 ( z)dz 1zЦТ центра тяжести
первого эпюра
В сумме получаем
J 1b k 1 z ЦТ 1 (b kzЦТ )
Выражение в скобках – значение функции f2 под центром
тяжести первой фигуры
J 1 f 2 ( z ЦТ )
ЦТ
h
ЦТ
h
ЦТ
h
l
l
l
l/2
lh / 3
lh / 2
lh
l /3
l/4
16.
Пример
Однопролетная двухконсольная балка нагружена силой и
моментом. Жесткость поперечного сечения на изгиб по
длине постоянна. Линейный размер l задан. Найти прогиб
сечения С от внешней нагрузки по абсолютной величине.
(Влиянием поперечной силы на величину перемещения
пренебречь).
1. Строим эпюр изгибающего момента от действительной
нагрузки
17.
2. Прикладываем единичную нагрузку в направлении
интересующего перемещения
3. Строим эпюр момента от приложенного единичного
фактора
18.
19. 3. Формула Мора для определения температурных перемещений сечения по заданному направлению
В основу вывода формулы положен принцип возможных перемещений
Пусть дана система, находящаяся под действием
температуры. Обозначим: n — число участков
системы; i — номер ее произвольного участка.
C
Для определения перемещения сечения С по
направлению v рассмотрим систему без температуры,
нагруженную безразмерной обобщенной единичной
B
силой, приложенной в сечении С по направлению v.
Схему системы под действием температуры
обозначим Т, а схему нагружения системы
обобщенной единичной силой обозначим 1. Приняв за
возможное перемещение системы ее
деформированное состояние в схеме Т, найдем
работу внешних, реактивных и упругих сил схемы
нагружения 1 на этом возможном перемещении. По
принципу возможных перемещений сумма этих работ
равна нулю, так как система в состоянии 1 находится B
в равновесии.
dS
G
v
D
T
dS
1
C
v
1
D
G
20.
Работа внешних сил
AP 1 v
dS
G
C
Опоры В и D неподвижны, а реакция в опоре G
направлена по нормали к любому ее возможному
перемещению, поэтому работа реактивных сил
v
B
AR 0
Для определения работы сил упругости Ау
рассмотрим один и тот же элемент, вырезанный из
схемы Т и схемы 1 двумя поперечными
сечениями, расcтояние dS между которыми
бесконечно мало.
Силы упругости в поперечном сечении элемента
могут привестись к шести внутренним силовым
факторам, которым присваиваем индекс 1.
D
T
dS
1
G
C
v
B
1
D
Обозначим температуры крайних верхних и нижних, правых и левых волокон i-го
участка соответственно Тв, Tн и Тп , Tл. Считаем, что температура в направлениях
осей у и z сечения изменяется линейно, будучи соответственно функцией только у
и только z.
21.
Законы изменения температуры по поперечному сечению показаны на рис.
TB
y z
Очевидно, что
TC
a
C N1
y
C
C’
x
x
z
b
M21
B B’
TC T y y 0 T z z 0
TH
dS
dδT
dS
B
TП
или
A
T(y)
A’
TЛ
Температура на оси
элемента
A
hy
T T
T b TH a
T y B Н y B
a b
a b
T TЛ
T с TЛ d
T z П
z П
с d
c d
TB b TH a TП с TЛ d
a b
c d
c
d
h2
T(z)
Пусть dδT — возможное перемещение центра тяжести поперечного сечения в
схеме от изменения температуры элемента.
d T TC dS
где α — коэффициент линейного расширения материала элемента.
Пусть dθTz — возможный относительный поворот концевых сечений элемента около
оси z в схеме от изменения температуры
T y
d zT
dS
hy
где T y TВ TН , h y — наибольший размер поперечного сечения в направлении оси
у.
22.
По аналогии, возможный относительный поворот концевых сечений элемента
вокруг оси y
Tz
d yT
dS
hz
где Tz TП TЛ , hz — наибольший размер поперечного сечения в направлении оси z.
1. dAy — работа сил упругости в элементе dS по абсолютной величине равна
работе внутренних силовых факторов состояния на возможных перемещениях
состояния и противоположна ей по знаку, так как силы упругости всегда
направлены в сторону, противоположную направлению изменения расстояния
между точками тела.
2. Работа МК1, Qy1 и Qz1 равна нулю, так как концевые сечения элемента при
нагреве относительно оси х не поворачиваются, a Qy1 и Qz1 перпендикулярны
направлению dδT, поэтому
dAy M z1d zT M y1d yT Nd T
Подставляя сюда полученные ранее выражения и интегрируя полученное
выражение по si —длине i-гo участка найдем работу сил упругости на i-м участке.
Ty
Tz
Ayi M z1
M y1
N1 Tc ds
hy
hz
si
23.
Суммируя эти интегралы по всем участкам системы, найдем Aу.
Ty
Tz
Ay M z1
M y1
N1 Tc ds
hy
hz
i 1 si
n
Складывая Ар с Ау и приравнивая сумму нулю, получим формулу Мора для
определения температурных перемещений сечений стержневой системы по
заданному направлению:
Ap Ay 0;
Ty
Tz
1 v M z1
M y1
N1 Tc ds 0;
hy
hz
i 1 si
n
Ty
Tz
v M z1
M y1
N1 Tc ds;
hy
hz
i 1 si
n
Источник