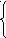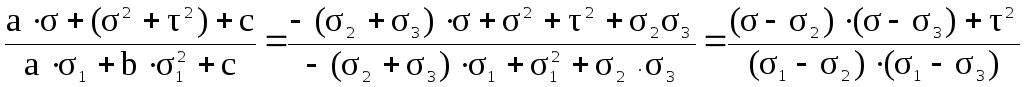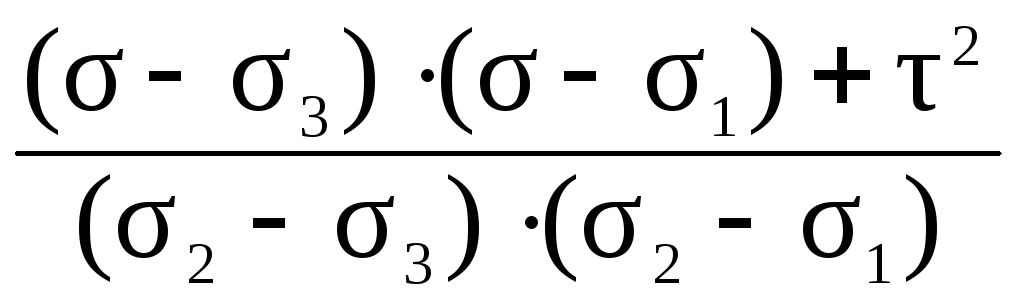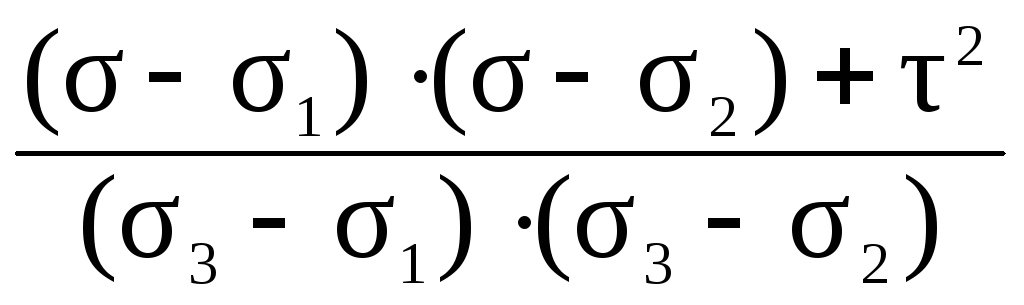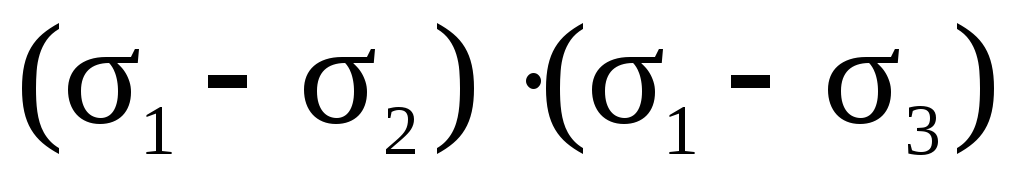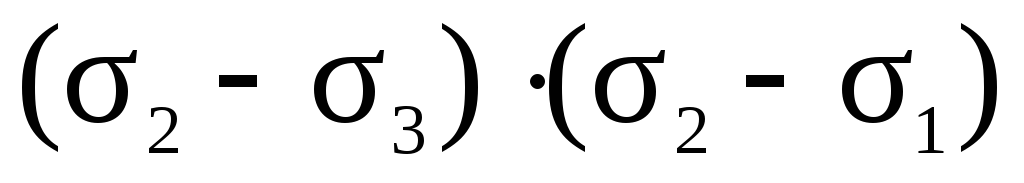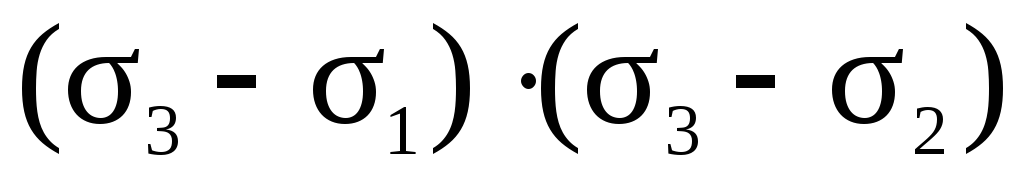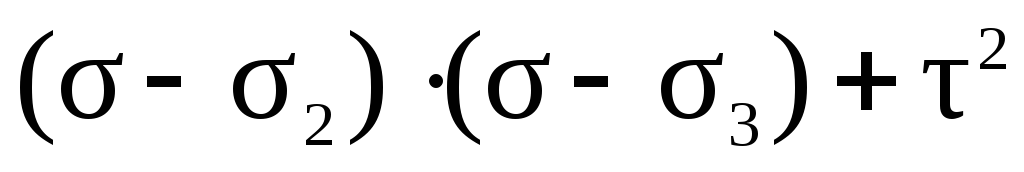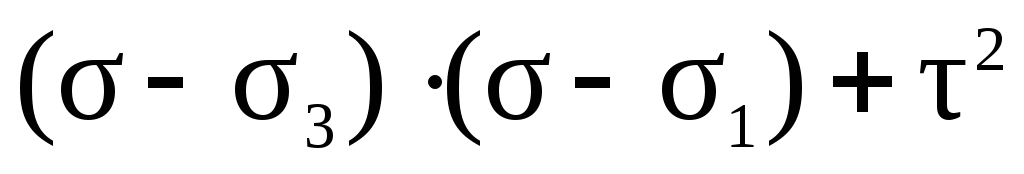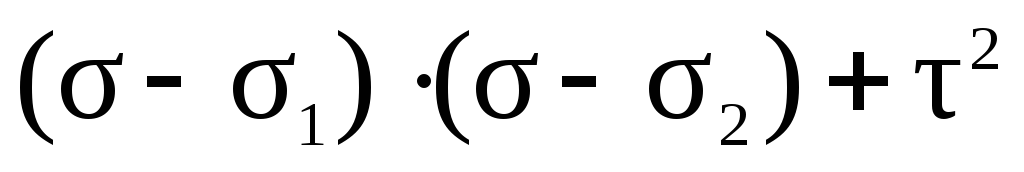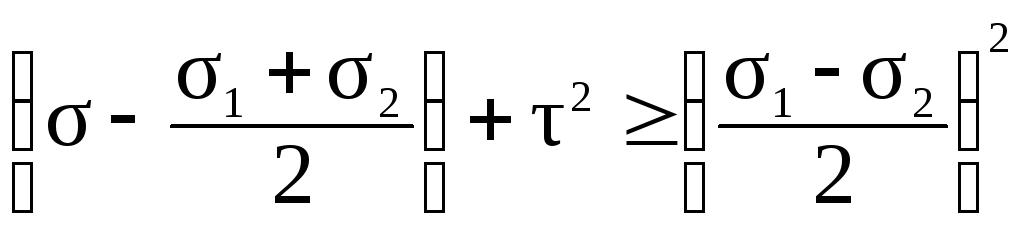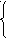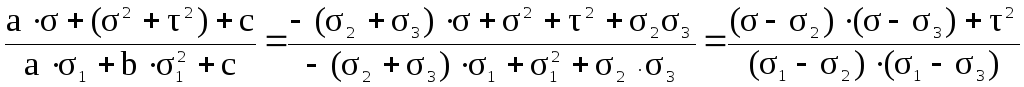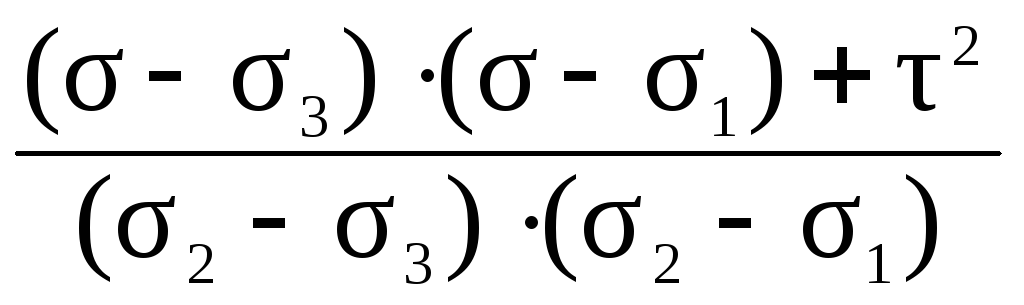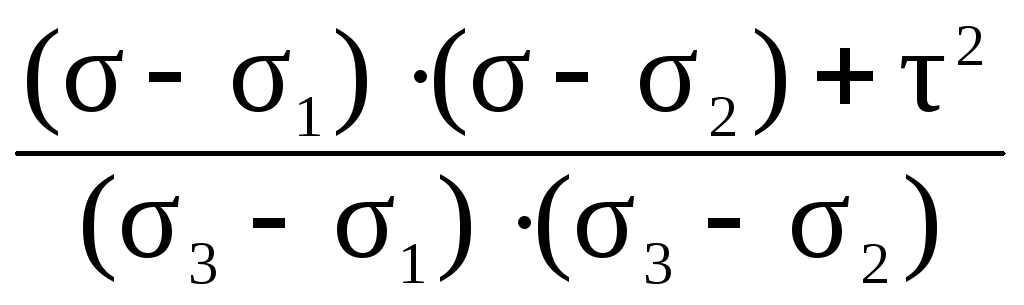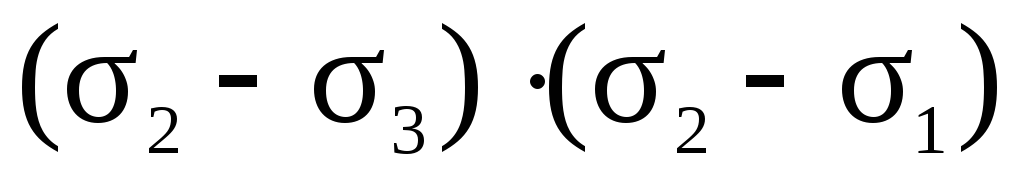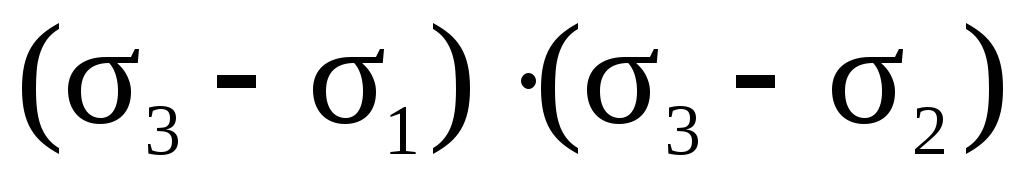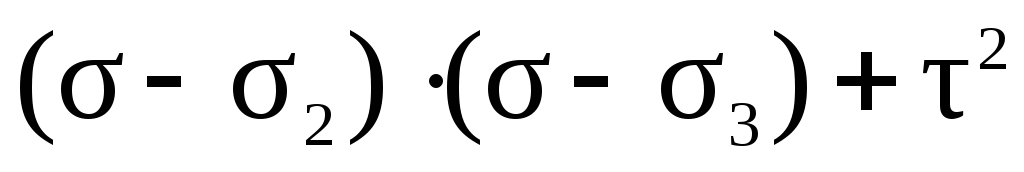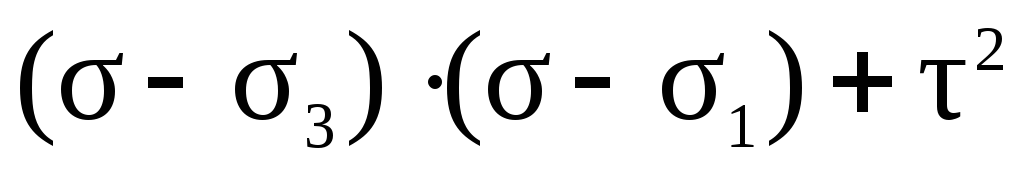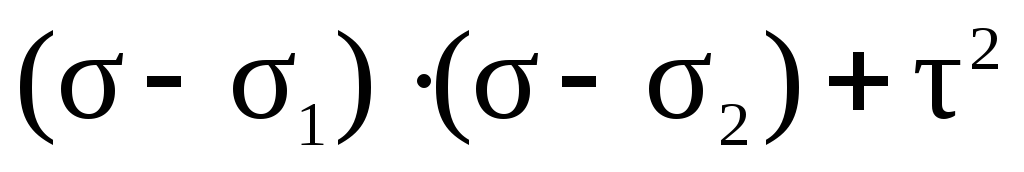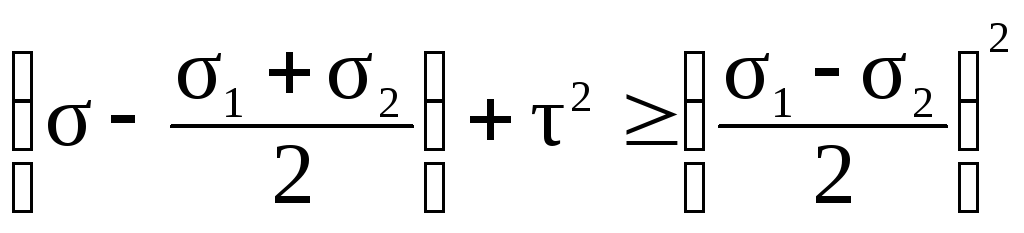Круговая диаграмма напряжений мора

11.10. Круги напряжений Мора

Удобное двумерное геометрическое представление трёхмерного напряжённого состояния было предложено немецким учёным О. Мором. Отнесём материальную частицу к главным осям (рис. 11.21). Рассечём её плоскостью, содержащей направление третьей главной оси (рис. 11.21,а). Тогда, согласно (11.35), имеем:

Уравнения (11.59) представляют собой параметрические уравнения окружности, каноническое уравнение которой имеет в системе координат вид (рис. 11.22):

Координаты центра окружности , радиус .

Окружность Мора позволяет графически найти напряжение на любой площадке, положение которой характеризуется углом Для этого нужно отложить по часовой стрелке угол и провести под этим углом радиус R до пересечения с окружностью в точке М. Координаты этой точки и есть искомое значения . Наибольшее касательное напряжение возникает при и равно численно радиусу окружности Мора:

Минимальное значение возникает на площадке при и равно:

Аналогичные круги Мора можно построить для наклонных площадок, содержащих главные направления 1 и 2 (рис. 11.23).

Их уравнения в параметрической форме имеют вид:

откуда следует, что наибольшее касательные напряжения в этих случаях:

также равны радиусам соответствующих кругов Мора.

носят название главных касательных напряжений. Они удовлетворяют тождеству

Каждой точке на любой из окружности Мора отвечают напряжения и площадки, направление которой характеризуется одним из углов Те площадки, которые не содержат ни одну из главных осей, окружностями Мора не описываются. Можно показать, что напряжения на этих площадках задаются точками, расположенными между окружностями в заштрихованной области. Из рис. 11.24 видно, что:

Следовательно, определяется радиусом большого круга Мора. Величину

называют параметром вида напряжённого состояния Лоде. При наложе-

нии на напряжённое состояние частицы всестороннего давления параметр Лоде не изменяется. Для одноосного растяжения имеем , для сжатия имеем , для плоского чистого сдвига . Соответствующие круги Мора приведены на рис. 11.25.

Таким образом, параметр Лоде характеризует вид напряжённого состояния.

Если изначально напряжённое состояние не является двухосным, связанным с главными осями, то для построения круга напряжений Мора при плоском напряжённом состоянии следует использовать формулы (11.35):

Поступая так же, как и в случае двухосного растяжения сводим пара-

метрические уравнения окружности (11.63) к каноническому виду

В (11.64) мы имеем более сложное выражение радиуса окружности:

При уравнение (11.64) сводится к (11.60) как частному случаю.

При построение круга Мора показано на рис. 11.26. Сначала определяется положение центра С круга как точки с координатами

Затем определяется положение точки А, характеризующей напряжения на грани х элемента при , т.е. . Здесь следует пом-

нить правило знаков для и других напряжений, указанных на

рис. 11.12. Заметим, что точки А и В, характеризующие напряжения на площадках, расположенных под углом 90 0 друг к другу, лежат на противо-

положных концах диаметра круга Мора. Далее на АВ с центром в точке С чертится круг. Напряжения на произвольной площадке, лежащей под углом к оси х, можно определить следующим образом. Отклады-

ваем от точки А по часовой стрелке угол и определяем положение точки М на круге с искомыми координатами . Точка М / , диаметра-

льно противоположная Д, даёт напряжения для площадки, состав-

ляющей угол 90 0 с той, которая имеет нормаль , т.е. для площадки с уг-

лом с осью х. Точка Д даёт максимальное касательное напряже-

ние, равное радиусу круга Мора:

Одной из важных задач использования круга Мора является определе-

ние главных нормальных напряжений и . Этим напряжениям отве-

чают точки Р₁ и Р₂ круга. Из рис. 11.26 следует, что угол между направле-

ниями на точки А и Р₁ равен удвоенному углу , определяющему первое главное напряжение, а угол между направлениями А и Р₂ – удвоенный угол , определяющий второе главное направление. Имеет место соотношение

которое совпадает с формулой (11.36).

Из изложенного следует, что круг Мора можно использовать в качес-

тве графического способа определения как напряжений на произвольной площадке, так и главных нормальных и максимальных касательных напря-

Источник

Экстремальные свойства главных напряжений. Круговая диаграмма Мора

Возьмем в теле произвольную точку А (х, у, z). Через эту точку можно провести бесконечное множество площадок. Очевидно, что на одной из площадок нормальное напряжение достигнет наибольшего для данной точки значения, а на другой касательное напряжение примет свое максимальное значение.

Пусть для точки А известно положение главных осей напряженного состояния. Если их принять за систему координат (рис.23), то в наклонной площадке с вектором нормали (l,m,n) возникают нормальные и касательные напряжения Р(,). Определим эти напряжения и исследуем их экстремальные свойства.

Нормальные напряжения в любой наклонной площадке выражаются основной квадратичной формой (33). Запишем её с учетом того, что в качестве системы координат приняты главные оси:

Найдем квадрат полного напряжения на наклонной площадке как сумму квадратов его проекций, выражения для которых были найдены ранее (32):

Также полное напряжение на наклонной площадке можно представить как сумму нормального и касательного напряжений (17).

Таким образом, мы имеем систему трех уравнений с тремя неизвестными — l 2 ,m 2 , n 2 :

 =₁l 2 +₂m 2 +₃n 2

Умножим каждое уравнение на произвольные множители a,b,cи сложим, сгруппировав при этом слагаемые по направляющим косинусам

Для определения величины l 2 подберем коэффициентыa,b,cтаким образом, чтобы вторая и третья скобки в правой части уравнения (41) обнулились:

Подставляя полученные коэффициенты в уравнение (41), находим величину l 2 :

l 2 =. (42)

Аналогично находим квадраты двух других направляющих косинусов

m 2 =,

n 2 =.

В уравнениях (42) и (43) дроби должны быть больше нуля, так как в левых частях стоят квадраты величин. Проанализируем знаменатели дробей на основе неравенства ₁ ₂ ₃:

 0,

 0, (44)

 0.

На основе неравенств (44) можно сделать вывод о знаке числителя:

 0,

 0, (45)

 0.

Сделав ряд математических преобразований, можно показать, что неравенства (45) представляют собой области, ограниченные окружностями. Рассмотрим третье неравенство и представим его решение графически (рис.24):

(46)

Представим решение системы (45) графически (рис.25). Эта диаграмма называется круговой диаграммой Мора. Круговая диаграмма позволяет установить экстремальные свойства нормальных и касательных напряжений.

Источник

Экстремальные свойства главных напряжений. Круговая диаграмма Мора

Возьмем в теле произвольную точку А (х, у, z). Через эту точку можно провести бесконечное множество площадок. Очевидно, что на одной из площадок нормальное напряжение достигнет наибольшего для данной точки значения, а на другой касательное напряжение примет свое максимальное значение.

Пусть для точки А известно положение главных осей напряженного состояния. Если их принять за систему координат (рис.23), то в наклонной площадке с вектором нормали (l,m,n) возникают нормальные и касательные напряжения Р(,). Определим эти напряжения и исследуем их экстремальные свойства.

Нормальные напряжения в любой наклонной площадке выражаются основной квадратичной формой (33). Запишем её с учетом того, что в качестве системы координат приняты главные оси:

Найдем квадрат полного напряжения на наклонной площадке как сумму квадратов его проекций, выражения для которых были найдены ранее (32):

Также полное напряжение на наклонной площадке можно представить как сумму нормального и касательного напряжений (17).

Таким образом, мы имеем систему трех уравнений с тремя неизвестными — l 2 ,m 2 , n 2 :

 =₁l 2 +₂m 2 +₃n 2

Умножим каждое уравнение на произвольные множители a,b,cи сложим, сгруппировав при этом слагаемые по направляющим косинусам

Для определения величины l 2 подберем коэффициентыa,b,cтаким образом, чтобы вторая и третья скобки в правой части уравнения (41) обнулились:

Подставляя полученные коэффициенты в уравнение (41), находим величину l 2 :

l 2 =. (42)

Аналогично находим квадраты двух других направляющих косинусов

m 2 =,

n 2 =.

В уравнениях (42) и (43) дроби должны быть больше нуля, так как в левых частях стоят квадраты величин. Проанализируем знаменатели дробей на основе неравенства ₁ ₂ ₃:

 0,

 0, (44)

 0.

На основе неравенств (44) можно сделать вывод о знаке числителя:

 0,

 0, (45)

 0.

Сделав ряд математических преобразований, можно показать, что неравенства (45) представляют собой области, ограниченные окружностями. Рассмотрим третье неравенство и представим его решение графически (рис.24):

(46)

Представим решение системы (45) графически (рис.25). Эта диаграмма называется круговой диаграммой Мора. Круговая диаграмма позволяет установить экстремальные свойства нормальных и касательных напряжений.

Источник

Билет 4

1.Теория напряжений. Круговая диаграмма о.Мора. Вывод формулы.

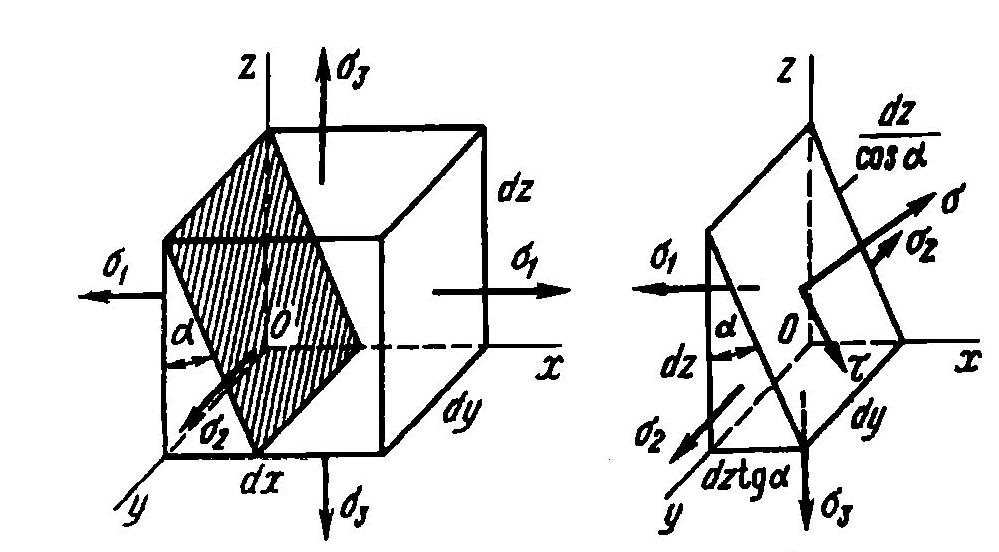
Рассмотрим условия равновесия треугольной призмы (рис). Она образована путем сечения элементарного параллелепипеда

наклонной площадкой, которая независимо от угла наклона αостается параллельной одной из главных осей(y)

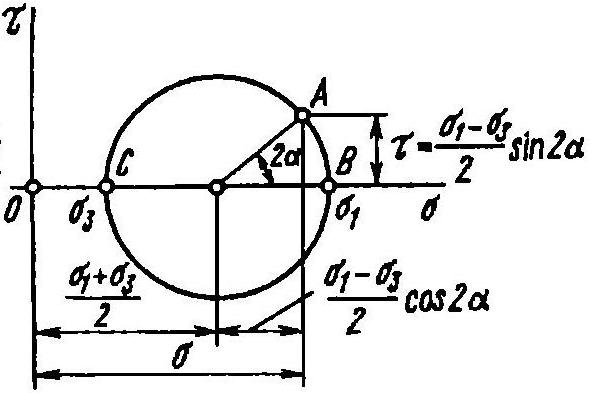
П роецируя все силы, действующие на отсеченную призму, на оси параллельные векторам α и τ :

– напряжения в семействе площадок параллельных 1 из гл. осей, можно дать геом. толкование:

; в системе координат,τ это есть ур-ие окружности, центр которой находится на расстоянии ) от нач.координат.. Окружность построенная на отрезке как

на диаметре называется Круговой диаграммой О.Мора. ( ур-ие окр)

2. Учет симметрии при решении статически неопределимых стержневых систем. Показать на примерах.

Билет 5

1. Расчеты на прочность при напряжениях, переменных во времени

Большинство деталей в различных машинах подвергаются действию циклически изменяющихся напряжений.

При циклическом изменении напряжений поломка деталей может происходить при напряжениях, значительно меньших, чем предел текучести.

Цикл- совокупность напряжений за период времени.

Циклы с одинаковыми R называются подобными.

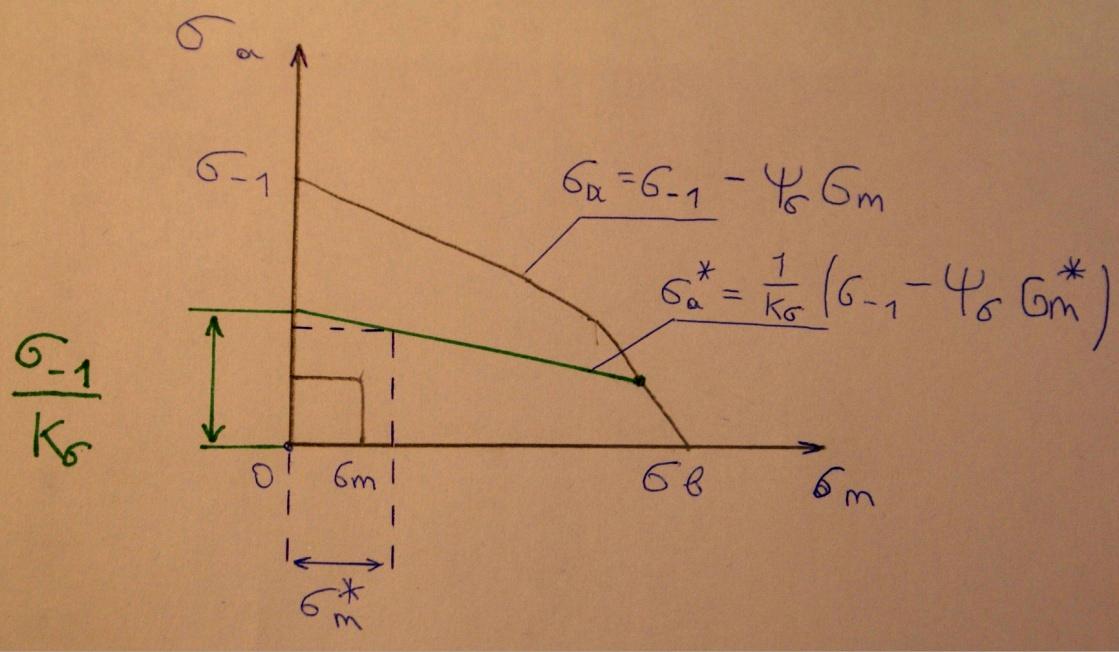
Определение коэффициента запаса по выносливости при одноосном напряженном состоянии.

Все полученный формулы применимы только при регулярном нагружении, при котором амплитуда и не меняются.

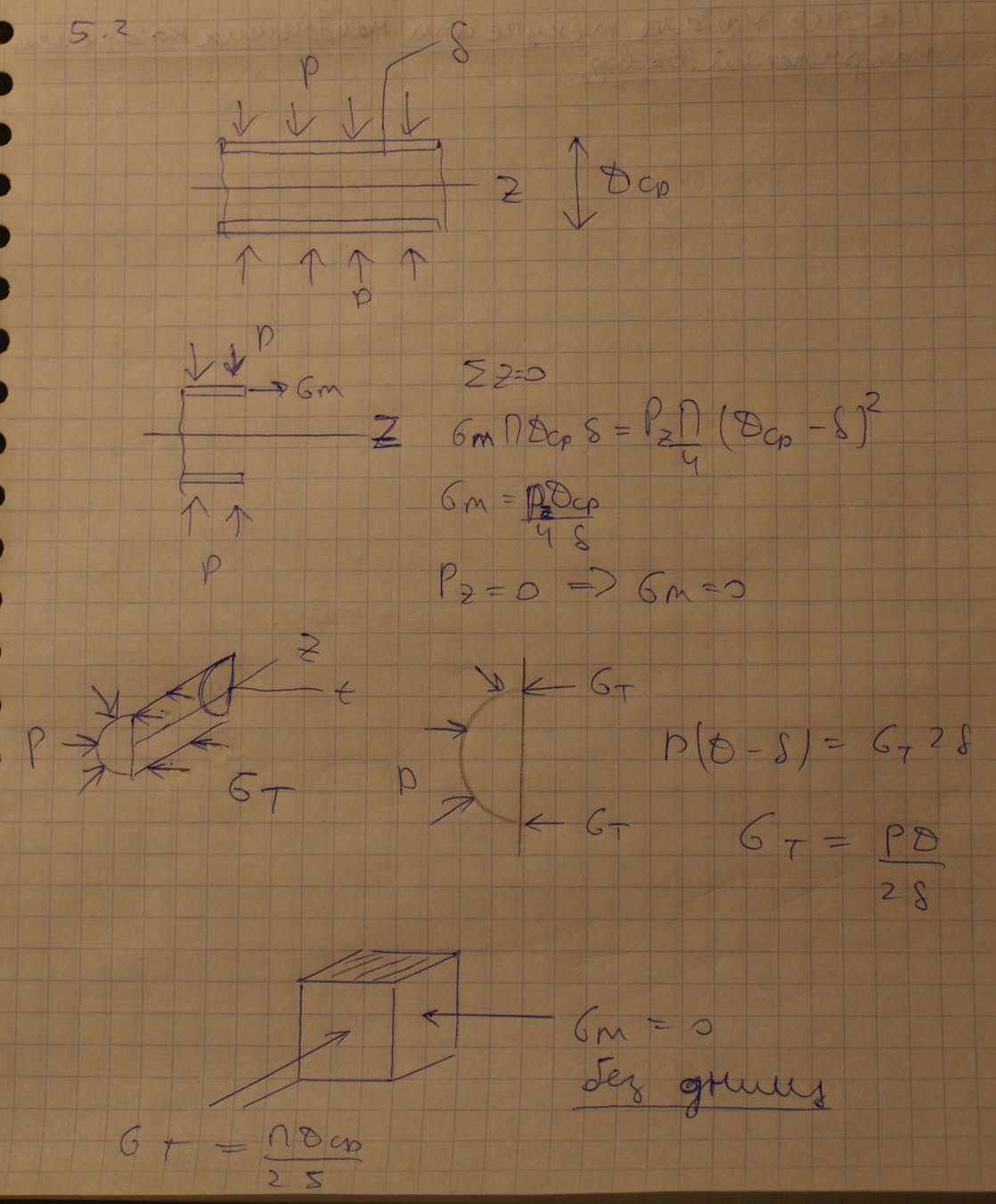
2.Напряжения, возникающие в тонкостенной трубке без днищ, нагруженной внешним давлением.

Билет 6

1. Теория начала текучести наибольших касательных напряжений. Вывод.

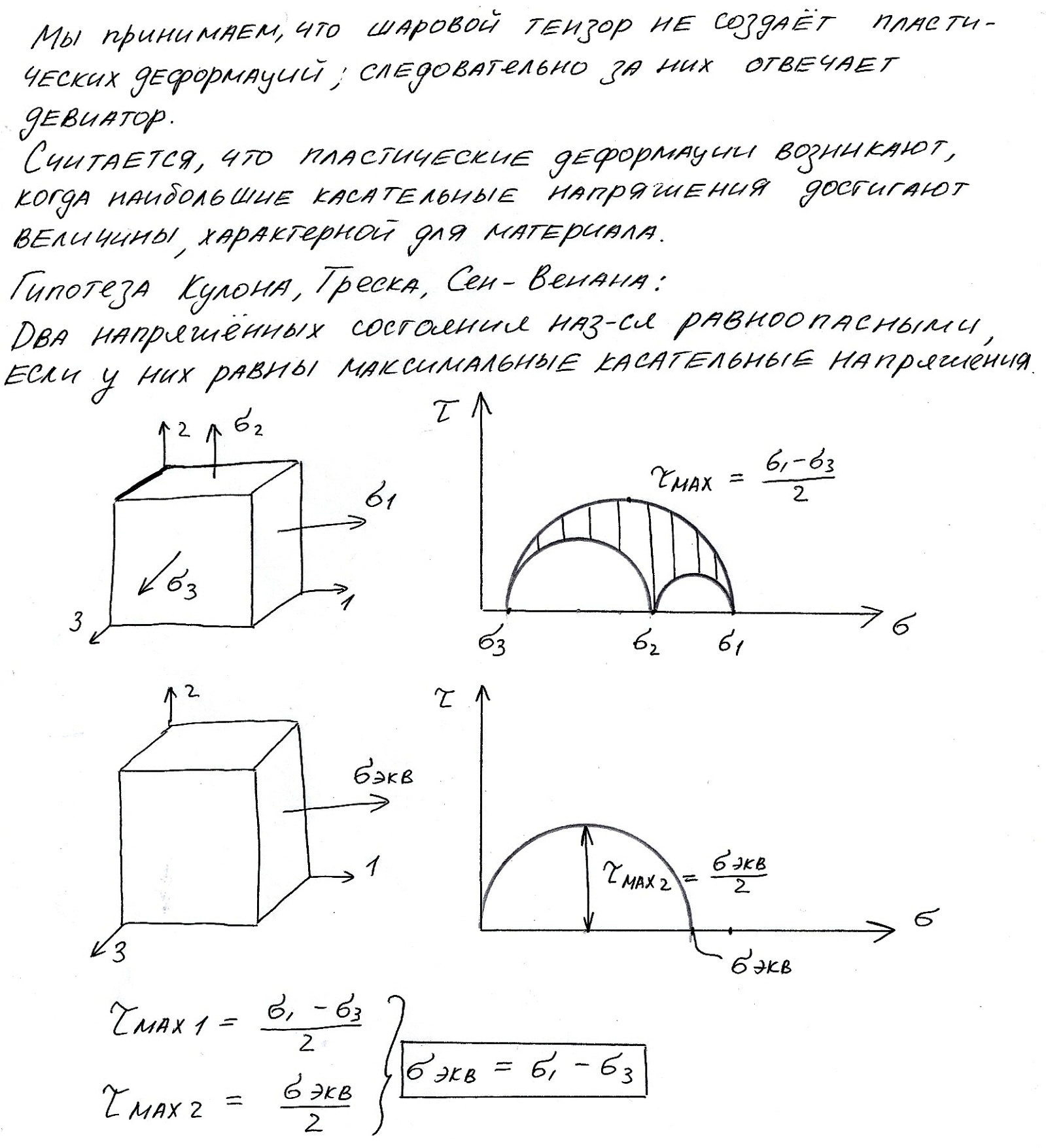
Мы принимаем, что шаровой тензор не создаёт пластических деформаций; следовательно за них отвечает девиатор.

Считается, что пластические деформации возникают, когда наибольшие касательные напряжения достигают величины, характерной для материала.

Гипотеза Кулона, Треска, Сен-Венана:

Два напряженных состояния называются равноопасными, если у них равны максимальные касательные напряжения.

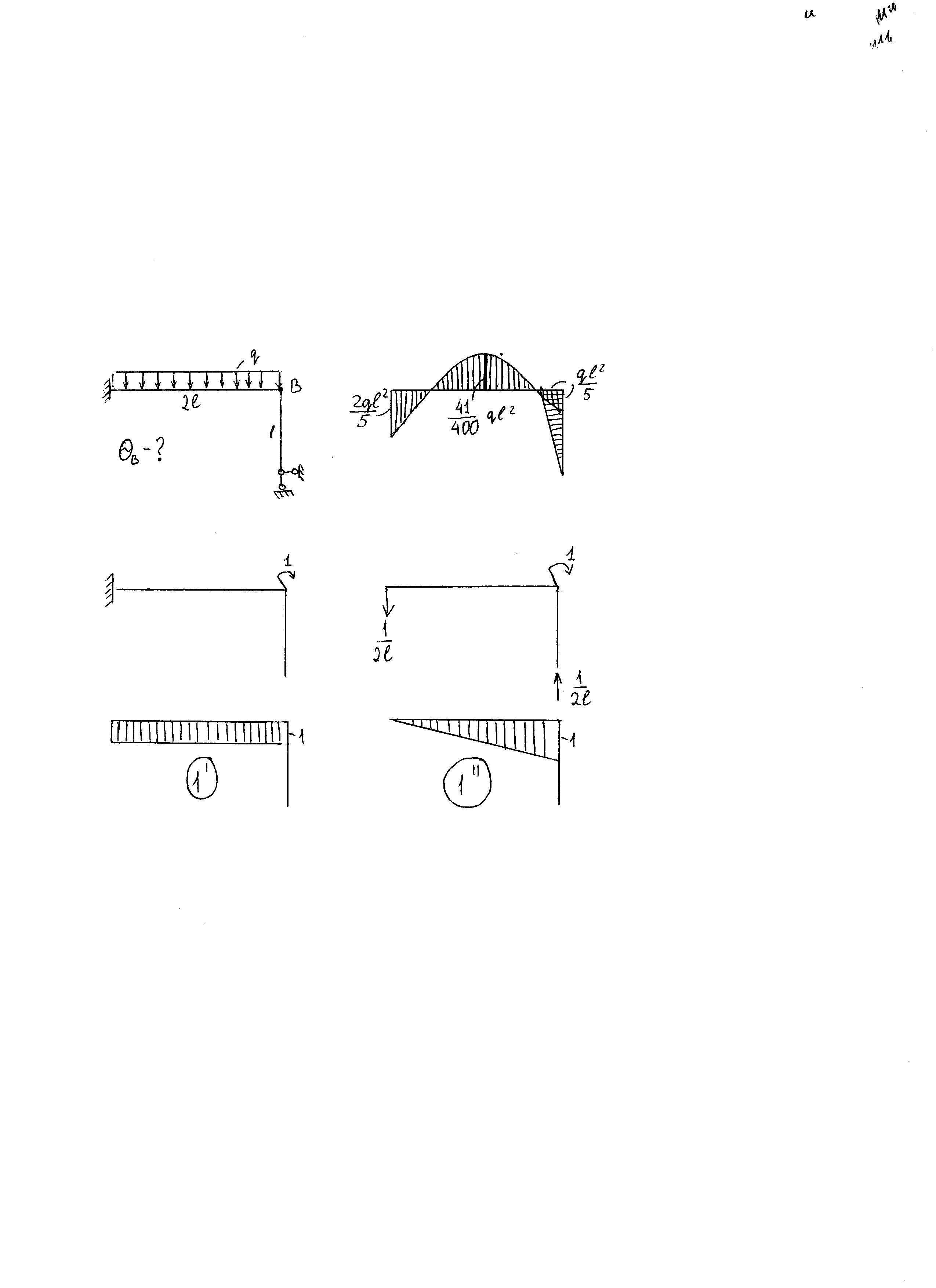
2. Определение перемещений в статически неопределимых стержневых системах

Перемещение ищем после того, как раскрыта статическая неопределённость и построена суммарная эпюра моментов.

Чтобы ещё раз не раскрывать статическую неопределённость, перемещение будем искать не для заданной системы, а для эквивалентной.

Для этого берём любую эквивалентную систему, разгружаем область внешних сил и, согласно интегралам Мора, прикладываем единичный фактор в направлении искомого перемещения.

После перемножаем суммарную эпюру М с эпюрой единичного фактора, используя графоаналитический способ взятия интегралов Мора.

Рассмотрим 2 эквивалентные системы:

Как видно, получили одинаковые результаты, т.е. от выбора эквивалентной системы ничего не зависит.

Источник