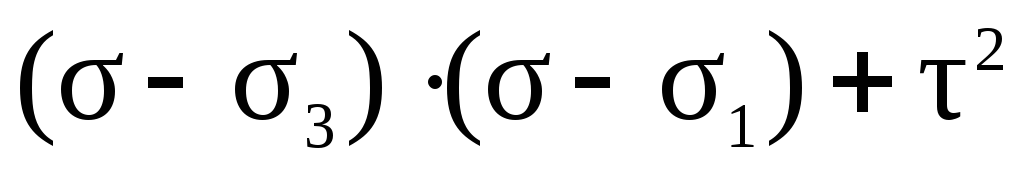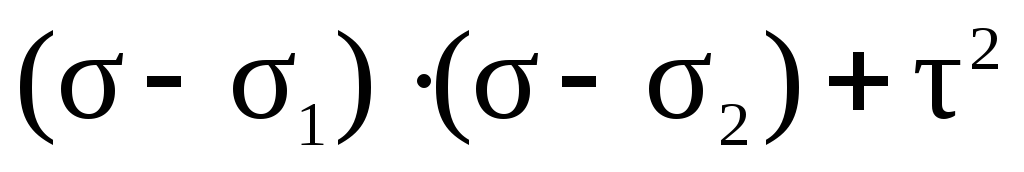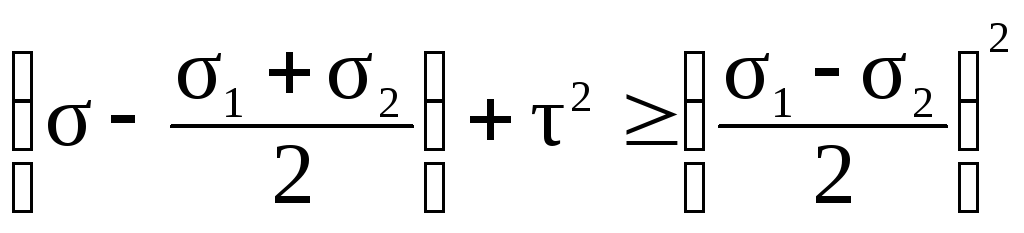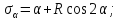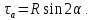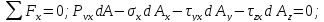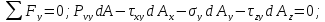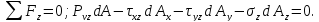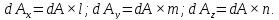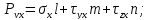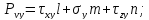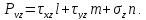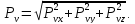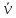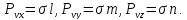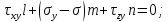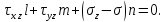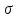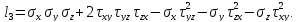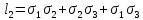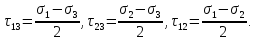11.10. Круги напряжений Мора
Удобное двумерное геометрическое представление трёхмерного напряжённого состояния было предложено немецким учёным О. Мором. Отнесём материальную частицу к главным осям (рис. 11.21). Рассечём её плоскостью, содержащей направление третьей главной оси (рис. 11.21,а). Тогда, согласно (11.35), имеем:
Уравнения (11.59) представляют собой параметрические уравнения окружности, каноническое уравнение которой имеет в системе координат вид (рис. 11.22):
Координаты центра окружности , радиус .
Окружность Мора позволяет графически найти напряжение на любой площадке, положение которой характеризуется углом Для этого нужно отложить по часовой стрелке угол и провести под этим углом радиус R до пересечения с окружностью в точке М. Координаты этой точки и есть искомое значения . Наибольшее касательное напряжение возникает при и равно численно радиусу окружности Мора:
Минимальное значение возникает на площадке при и равно:
Аналогичные круги Мора можно построить для наклонных площадок, содержащих главные направления 1 и 2 (рис. 11.23).
Их уравнения в параметрической форме имеют вид:
откуда следует, что наибольшее касательные напряжения в этих случаях:
также равны радиусам соответствующих кругов Мора.
носят название главных касательных напряжений. Они удовлетворяют тождеству
Каждой точке на любой из окружности Мора отвечают напряжения и площадки, направление которой характеризуется одним из углов Те площадки, которые не содержат ни одну из главных осей, окружностями Мора не описываются. Можно показать, что напряжения на этих площадках задаются точками, расположенными между окружностями в заштрихованной области. Из рис. 11.24 видно, что:
Следовательно, определяется радиусом большого круга Мора. Величину
называют параметром вида напряжённого состояния Лоде. При наложе-
нии на напряжённое состояние частицы всестороннего давления параметр Лоде не изменяется. Для одноосного растяжения имеем , для сжатия имеем , для плоского чистого сдвига . Соответствующие круги Мора приведены на рис. 11.25.
Таким образом, параметр Лоде характеризует вид напряжённого состояния.
Если изначально напряжённое состояние не является двухосным, связанным с главными осями, то для построения круга напряжений Мора при плоском напряжённом состоянии следует использовать формулы (11.35):
Поступая так же, как и в случае двухосного растяжения сводим пара-
метрические уравнения окружности (11.63) к каноническому виду
В (11.64) мы имеем более сложное выражение радиуса окружности:
При уравнение (11.64) сводится к (11.60) как частному случаю.
При построение круга Мора показано на рис. 11.26. Сначала определяется положение центра С круга как точки с координатами
Затем определяется положение точки А, характеризующей напряжения на грани х элемента при , т.е. . Здесь следует пом-
нить правило знаков для и других напряжений, указанных на
рис. 11.12. Заметим, что точки А и В, характеризующие напряжения на площадках, расположенных под углом 90 0 друг к другу, лежат на противо-
положных концах диаметра круга Мора. Далее на АВ с центром в точке С чертится круг. Напряжения на произвольной площадке, лежащей под углом к оси х, можно определить следующим образом. Отклады-
ваем от точки А по часовой стрелке угол и определяем положение точки М на круге с искомыми координатами . Точка М / , диаметра-
льно противоположная Д, даёт напряжения для площадки, состав-
ляющей угол 90 0 с той, которая имеет нормаль , т.е. для площадки с уг-
лом с осью х. Точка Д даёт максимальное касательное напряже-
ние, равное радиусу круга Мора:
Одной из важных задач использования круга Мора является определе-
ние главных нормальных напряжений и . Этим напряжениям отве-
чают точки Р1 и Р2 круга. Из рис. 11.26 следует, что угол между направле-
ниями на точки А и Р1 равен удвоенному углу , определяющему первое главное напряжение, а угол между направлениями А и Р2 – удвоенный угол , определяющий второе главное направление. Имеет место соотношение
которое совпадает с формулой (11.36).
Из изложенного следует, что круг Мора можно использовать в качес-
тве графического способа определения как напряжений на произвольной площадке, так и главных нормальных и максимальных касательных напря-
Источник
Экстремальные свойства главных напряжений. Круговая диаграмма Мора
Возьмем в теле произвольную точку А (х, у, z). Через эту точку можно провести бесконечное множество площадок. Очевидно, что на одной из площадок нормальное напряжение достигнет наибольшего для данной точки значения, а на другой касательное напряжение примет свое максимальное значение.
Пусть для точки А известно положение главных осей напряженного состояния. Если их принять за систему координат (рис.23), то в наклонной площадке с вектором нормали (l,m,n) возникают нормальные и касательные напряжения Р(,). Определим эти напряжения и исследуем их экстремальные свойства.
Нормальные напряжения в любой наклонной площадке выражаются основной квадратичной формой (33). Запишем её с учетом того, что в качестве системы координат приняты главные оси:
Найдем квадрат полного напряжения на наклонной площадке как сумму квадратов его проекций, выражения для которых были найдены ранее (32):
Также полное напряжение на наклонной площадке можно представить как сумму нормального и касательного напряжений (17).
Таким образом, мы имеем систему трех уравнений с тремя неизвестными — l 2 ,m 2 , n 2 :
=1l 2 +2m 2 +3n 2
Умножим каждое уравнение на произвольные множители a,b,cи сложим, сгруппировав при этом слагаемые по направляющим косинусам
Для определения величины l 2 подберем коэффициентыa,b,cтаким образом, чтобы вторая и третья скобки в правой части уравнения (41) обнулились:
Подставляя полученные коэффициенты в уравнение (41), находим величину l 2 :
l 2 =. (42)
Аналогично находим квадраты двух других направляющих косинусов
m 2 =,
n 2 =.
В уравнениях (42) и (43) дроби должны быть больше нуля, так как в левых частях стоят квадраты величин. Проанализируем знаменатели дробей на основе неравенства 1 2 3:
0,
0, (44)
0.
На основе неравенств (44) можно сделать вывод о знаке числителя:
0,
0, (45)
0.
Сделав ряд математических преобразований, можно показать, что неравенства (45) представляют собой области, ограниченные окружностями. Рассмотрим третье неравенство и представим его решение графически (рис.24):
(46)
Представим решение системы (45) графически (рис.25). Эта диаграмма называется круговой диаграммой Мора. Круговая диаграмма позволяет установить экстремальные свойства нормальных и касательных напряжений.
Источник
7.6. Круг напряжений Мора
Зависимость напряжений от угла наклона площадки, на которой они действуют, имеет простую геометрическую интерпретацию в виде диаграммы, которая называется кругом напряжений Мора. Обозначим:
Тогда напряжения на наклонных площадках можно представить в виде:
Эти уравнения представляют окружность в параметрической форме. Они эквивалентны уравнению:
Используя круги Мора, можно решать два типа задач.
Первый тип. Пусть известны напряжения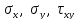 
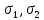
на произволь-ных площадках. Требуется найти главные напряжения 
и положение главных площадок.
Решение. По оси 
(рис. 7.6) отложим отрезок 
, равный по величине 
Рис. 7.6. Схема круга Мора для нахождения главных напряжений
и положения главных площадок
Из точки 
в направлении оси 
отложим отрезок 
соответствующий 
. Аналогично построим точки
, равные напряжениям
. Соединив точки 
, получим точку С пересечения отрезка 
с осью 
. Вокруг точки С опишем окружность диаметром
. Это и будет окружность напряжений Мора.
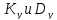
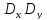
Точки А и В пересечения окружности с осью σ соответствуют главным напряжениям
. Для определения направления главных площадок из точки 
проведем прямую параллельно оси 
до пересечения с окружностью в точке М, которая называется полюсом. Прямые, проведенные из полюса в точки А и В, соответствуют направлению главных напряжений
соответственно.
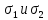
Второй тип. Пусть известны главные напряжения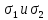
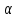
. Требуется определить напряжения на площадках, направленных под углом 
к главным.
Решение. Вдоль оси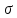 
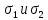
(рис. 7.7, б) отложим отрезки ОА и ОВ, соответствующие главным напряжениям 
. На отрезке АВ, как на диаметре, построим окружность напряжений Мора. Из центра окружности (точка С) отложим центральный угол 2α с осью σ и проведем прямую до пересечения с окружностью в точках Dα и Dβ.
Рис. 7.7. Схема круга Мора для нахождения напряжений
на второстепенных площадках
Координаты этих точек соответствуют напряжениям на площадках, повернутых на угол и на площадке, на которой действует главное напряжение 
. Положения этих площадок получим, проведя из точки В прямые до пересечения с окружностью в точках 
.
7.7. Объемное напряженное состояние
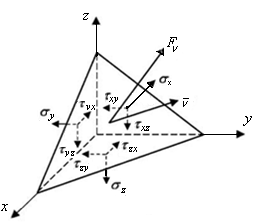
В общем случае напряженного состояния на гранях элементарного параллелепипеда, выделенного в окрестности точки нагруженного тела, действует девять компонентов тензора напряжений. В силу закона парности касательных напряжений независимыми являются только шесть из них.
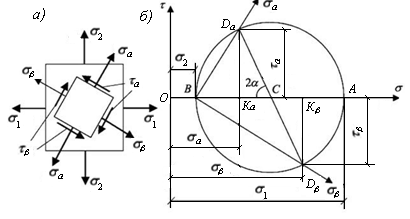
Вычислим напряжения на произвольной площадке ABC с вектором нормали ν в окрестности произвольной точки О (см. рис. 7.7). Обозначим направляющие косинусы вектора нормали ν к площадке ABC величинами:
Проекции полного напряжения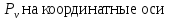
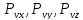
, действующего на площадке АВС, обозначим 
. Для их определения составим уравнения равновесия четырехгранника, выделенного координатными плоскостями и плоскостью АВС в окрестности произвольной точки нагруженного тела (рис. 7.8):
Площади граней элементов связаны между собой зависимостями:
Нормальные напряжения найдем, составив сумму проекций на направление нормали:
Полное напряжение на площадке:
Касательное напряжение на площадке:
.
Определение главных напряжений.
Пусть площадка АВС (рис. 7.8) – главная, а нормаль к ней совпадает с главной осью. Касательные напряжения на этой грани отсутствуют, а нормальное напряжение совпадает с полным. Проекции этого напряжения на координатные оси равны:
Учитывая выражение для , получим:
Эти равенства можно рассматривать, как однородную систему линейных алгебраических уравнений относительно l, m и n.
Рис. 7.8. Схема площадки для определения
Так как направляющие косинусы связаны соотношениями l + m + n = 1, нулевое решение этой системы невозможно. Нулевое решение системы возможно только в том случае, когда определитель, составленный из ее коэффициентов при неизвестных, обращается в нуль, т. е.
.
Раскрыв этот определитель, получим кубическое уравнение относительно главного напряжения :
где
В силу симметрии определителя относительно главной диагонали, соответствующее ему кубическое уравнение имеет три действительных корня, три главных напряжения: .
Главные напряжения в точке нагруженного тела не зависят от выбора системы координат. Поэтому
и называют их соответственно первым, вторым и третьим инвариантами тензора напряжений. Их можно представить в виде:
;
;
В случае объемного напряженного состояния напряжения также можно представить графически. Если рассмотреть наклонные площадки, параллельные одному из главных напряжений, то для них справедливы формулы для плоского напряженного состояния. Из рис. 7.9 видно, что напряжение σ3 не влияет на величину напряжений σα и τα, действующих на площадке, параллельной σ3. Тогда напряжения на таких площадках можно представить графически, построив круг Мора на главных напряжениях σ1 и σ2. Аналогично можно представить графически напряжения на наклонных площадках, параллельных σ1 и σ2, как показано на рис. 7.10. Однако точки, расположенные на этих трех кругах, не исчерпывают всех наклонных площадок в точке нагруженного тела.
Рис. 7.9. Схема наклонной площадки при объемном
Можно показать, что площадкам общего положения соответствуют точки на плоскости, лежащие в заштрихованной области между тремя кругами Мора. Точки, являющиеся вершинами этих кругов, соответствуют площадкам, наклоненным под углом 45 о к соответствующим главным площадкам.
Рис. 7.10. Круги Мора для определения
Касательные напряжения на этих площадках равны радиусам кругов Мора и определяются формулами:
Максимальное касательное напряжение
Источник