Основные уравнения теории предельного равновесия
Построение круга Мора производится в следующей последовательности. От начала координат откладываем значения σ 1 и σ 3 . Из точки В проводят окружность радиусомт R . Любая точка E на окружности характеризует напряженное состояние грунта в плоскости, проходящей через рассматриваемую точку. Угол наклона α линии ЕА — это угол наклона рассматриваемой площадки к главной. Центральный угол наклона отрезка EB равен 2α. Нормальные напряжения по этой площадке а представляются по горизонтальной оси отрезком ОЕ’, касательные τ — перпендикулярным отрезком ЕЕ’ .
Значения σ и τ могут быть определены через σ 1 и σ 3 по формулам (8.1) и (8.2).
Максимальные и минимальные касательные напряжения соответствуют sin 2α = 1 и sin 2α = -1, т.е. углам 2α=π/2 или 3π/2 (α=45° или 135°).
Полное результирующее напряжение на рассматриваемой площадке
Угол отклонения σ n от нормали к площадке
Значение угла θ при изменении угла α от 0 до 90° сначала возрастает от нуля до некоторого θ max , а затем убывает до нуля.
Угол θ максимален, когда линия ОE станет касательной к кругу напряжений. Из треугольника ОBЕ :
Максимальное отклонение полного (результирующего) напряжения на угол θmax нормали к площадке имеет место при:
Следовательно, отклонения площадки скольжения от направления наибольшего главного напряжения σ 1
Таким образом, в предельном состоянии в каждой точке грунта имеются две сопряженные площадки скольжения, наклоненные под углом 45°- φ/2 к линии действия максимального и 45° + φ/2 — минимального главного напряжения ( рис. 8.3 ).
Рис. 8.3. Ориентация площадок скольжения относительно главных напряжений: 1, 2 — площадки скольжения
Для сыпучих грунтов во всех случаях θ max не может быть больше угла внутреннего трения φ. А разрушение сыпучих грунтов наступает, когда угол отклонения полного(результирующего) напряжения равен углу внутреннего трения:
Выражение (8.8) является условием прочности грунта. Тогда уравнение предельного равновесия можно записать в следующем виде:
Выражение (8.9) известно в механике грунтов как условие прочности (предельного равновесия) для песчаных (сыпучих) грунтов. После несложных тригонометрических преобразований это выражение можно записать в следующем виде:
Это выражение часто используют в теории давления грунтов на ограждения (глава 10). Для связных грунтов также можно записать условие предельного равновесия, предварительно построив круги Мора ( рис. 8.4 ) по результатам испытания в стабилометре (см. рис. 5.7).
Рис. 8.4. Круги Мора, построенные по результатам испытания образцов грунта на сжатие в стабилометре
а отрезок О’Д можно найти из выражения
Отрезок О ‘О , отсекаемый наклонной линией на оси абсцисс (см. рис. 8.4), называют давлением связности, которое можно представить в виде
Давление связности (8.14) можно условно считать начальным давлением связного грунта, которое необходимо преодолеть при испытании на сдвиг. Зная ВД (8.12) и О’Д (8.13), а также используя (8.14), найдем
Выражение (8.15), связывающее главные напряжения в момент разрушения образца с углом внутреннего трения, принято называть уравнением предельного равновесия для связных грунтов.
Уравнение (8.15) в некоторых случаях удобно использовать не в главных напряжениях, а в компонентах, записанных относительно координатных осей. Из сопротивления материалов известно, что:
Тогда, рассматривая совместно уравнения (8.15) и (8.16), можно записать уравнение предельного равновесия в следующем виде:
Аналогичным образом можно выразить и уравнение (8.9).
Источник
11.10. Круги напряжений Мора
Удобное двумерное геометрическое представление трёхмерного напряжённого состояния было предложено немецким учёным О. Мором. Отнесём материальную частицу к главным осям (рис. 11.21). Рассечём её плоскостью, содержащей направление третьей главной оси (рис. 11.21,а). Тогда, согласно (11.35), имеем:
Уравнения (11.59) представляют собой параметрические уравнения окружности, каноническое уравнение которой имеет в системе координат вид (рис. 11.22):
Координаты центра окружности , радиус .
Окружность Мора позволяет графически найти напряжение на любой площадке, положение которой характеризуется углом Для этого нужно отложить по часовой стрелке угол и провести под этим углом радиус R до пересечения с окружностью в точке М. Координаты этой точки и есть искомое значения . Наибольшее касательное напряжение возникает при и равно численно радиусу окружности Мора:
Минимальное значение возникает на площадке при и равно:
Аналогичные круги Мора можно построить для наклонных площадок, содержащих главные направления 1 и 2 (рис. 11.23).
Их уравнения в параметрической форме имеют вид:
откуда следует, что наибольшее касательные напряжения в этих случаях:
также равны радиусам соответствующих кругов Мора.
носят название главных касательных напряжений. Они удовлетворяют тождеству
Каждой точке на любой из окружности Мора отвечают напряжения и площадки, направление которой характеризуется одним из углов Те площадки, которые не содержат ни одну из главных осей, окружностями Мора не описываются. Можно показать, что напряжения на этих площадках задаются точками, расположенными между окружностями в заштрихованной области. Из рис. 11.24 видно, что:
Следовательно, определяется радиусом большого круга Мора. Величину
называют параметром вида напряжённого состояния Лоде. При наложе-
нии на напряжённое состояние частицы всестороннего давления параметр Лоде не изменяется. Для одноосного растяжения имеем , для сжатия имеем , для плоского чистого сдвига . Соответствующие круги Мора приведены на рис. 11.25.
Таким образом, параметр Лоде характеризует вид напряжённого состояния.
Если изначально напряжённое состояние не является двухосным, связанным с главными осями, то для построения круга напряжений Мора при плоском напряжённом состоянии следует использовать формулы (11.35):
Поступая так же, как и в случае двухосного растяжения сводим пара-
метрические уравнения окружности (11.63) к каноническому виду
В (11.64) мы имеем более сложное выражение радиуса окружности:
При уравнение (11.64) сводится к (11.60) как частному случаю.
При построение круга Мора показано на рис. 11.26. Сначала определяется положение центра С круга как точки с координатами
Затем определяется положение точки А, характеризующей напряжения на грани х элемента при , т.е. . Здесь следует пом-
нить правило знаков для и других напряжений, указанных на
рис. 11.12. Заметим, что точки А и В, характеризующие напряжения на площадках, расположенных под углом 90 0 друг к другу, лежат на противо-
положных концах диаметра круга Мора. Далее на АВ с центром в точке С чертится круг. Напряжения на произвольной площадке, лежащей под углом к оси х, можно определить следующим образом. Отклады-
ваем от точки А по часовой стрелке угол и определяем положение точки М на круге с искомыми координатами . Точка М / , диаметра-
льно противоположная Д, даёт напряжения для площадки, состав-
ляющей угол 90 0 с той, которая имеет нормаль , т.е. для площадки с уг-
лом с осью х. Точка Д даёт максимальное касательное напряже-
ние, равное радиусу круга Мора:
Одной из важных задач использования круга Мора является определе-
ние главных нормальных напряжений и . Этим напряжениям отве-
чают точки Р1 и Р2 круга. Из рис. 11.26 следует, что угол между направле-
ниями на точки А и Р1 равен удвоенному углу , определяющему первое главное напряжение, а угол между направлениями А и Р2 – удвоенный угол , определяющий второе главное направление. Имеет место соотношение
которое совпадает с формулой (11.36).
Из изложенного следует, что круг Мора можно использовать в качес-
тве графического способа определения как напряжений на произвольной площадке, так и главных нормальных и максимальных касательных напря-
Источник
Решение плоской задачи о.К. Мора Прямая задача Мора
Прямая задача Мора – это задача определения напряжений на произвольной площадке по известным главным напряжениям. Рассмотрим элементарный объем, находящийся в условиях объемного напряженного состояния, причем грани этого объема являются главными площадками. Секущей площадкой, параллельной главному напряжению σ2, выделим из этого объема треугольную призму: 

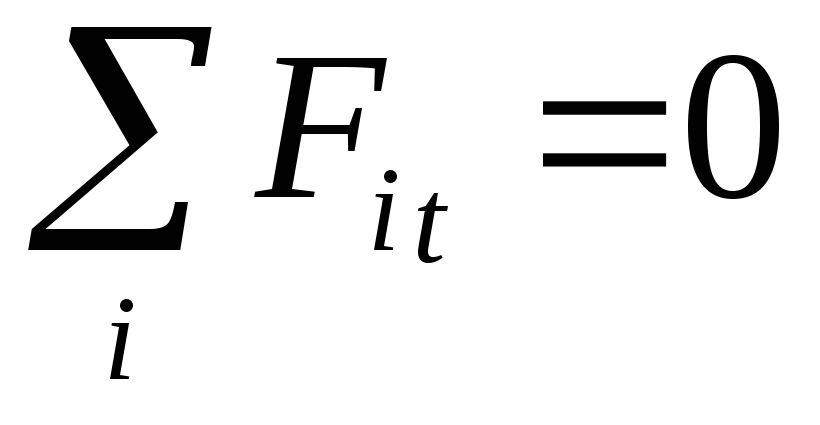










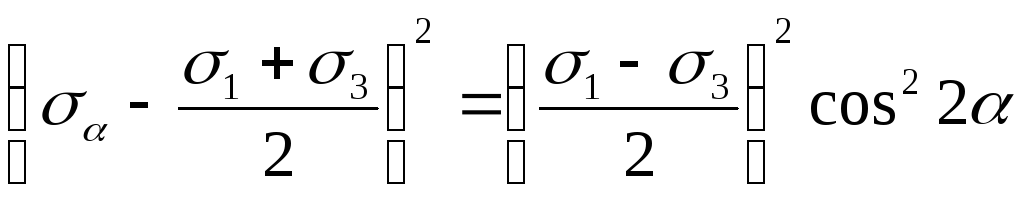











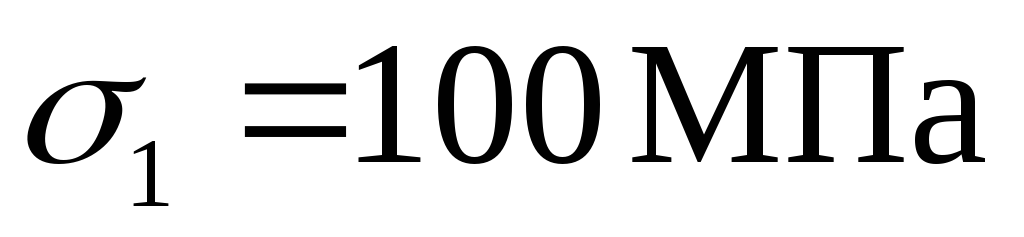




Обратная задача Мора
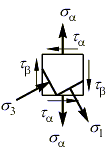
Обратная задача Мора состоит в определении главных напряжений по известным напряжениям на произвольной площадке. Рассмотрим её на конкретном примере. Задача. Определить главные напряжения в опасной точке стержня, подвергающегося совместному действию изгиба и кручения: 









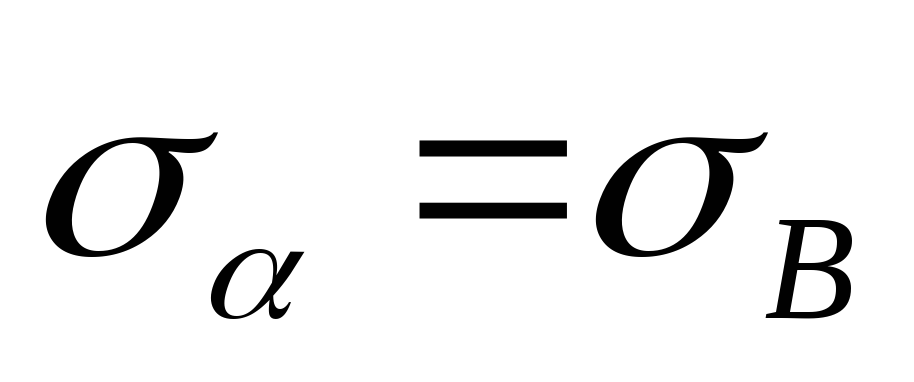


- В системе координат нанести точки с координатами
(,) и
(,). При этом нормальное напряжение считается положительным, если оно вызывает растяжение, а касательное – если оно действует по часовой стрелке относительно центра элемента.
- Соединить полученные точки DиDотрезком. Точка пересечения этого отрезка с осью абсциссOявляется центром круга Мора.
- Построить окружность с центром в точке Oи радиусомOD. Координаты точек пересечения окружности с осью абсцисс дают величины главных напряжений (в нашем случае, и).
- Пересечение площадок (горизонталь) и(вертикаль) дает положение полюса площадок круга МораPпл(точка, в которой пересекаются все площадки).
- Провести из полюса Pпллучи через точки (, 0) и (, 0). Эти лучи задают положение главных площадок.

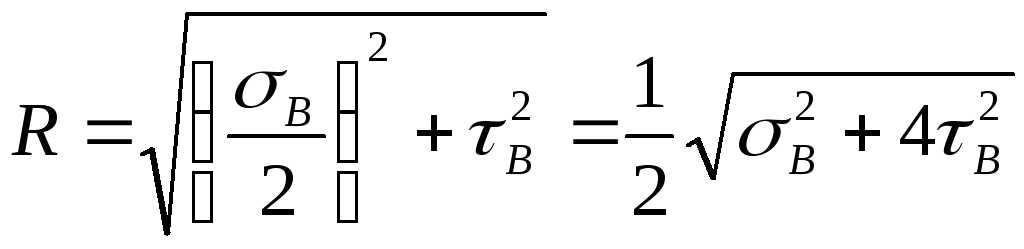


Источник

 (,) и
(,) и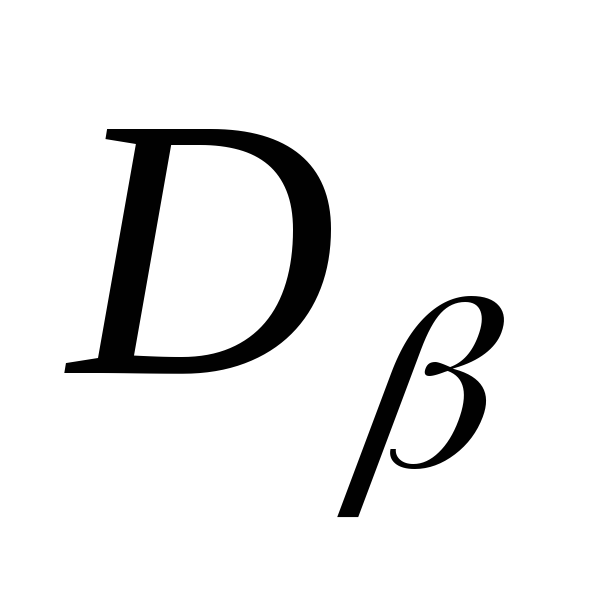 (,). При этом нормальное напряжение считается положительным, если оно вызывает растяжение, а касательное – если оно действует по часовой стрелке относительно центра элемента.
(,). При этом нормальное напряжение считается положительным, если оно вызывает растяжение, а касательное – если оно действует по часовой стрелке относительно центра элемента.