Калькулятор атмосферного давления от высоты над уровнем моря

Зависимость температуры кипения воды от высоты над уровнем моря

После создания пары калькуляторов на тему давления вообще (Конвертер единиц давления) и атмосферного давления в частности (Барометрическое нивелирование), захотелось узнать, как рассчитать температуру кипения воды в зависимости от высоты. Я откуда-то знал, что на высоте вода кипит при температуре ниже 100°С — а вот при какой точно температуре она кипит — вопрос.

Задача состоит из двух этапов — установить зависимость атмосферного давления от высоты и зависимость температуры кипения от давления. Начнем с последнего, как с более интересного.

Кипение представляет собой фазовый переход первого рода (вода сменяет агрегатное состояние из жидкого на газообразное).
Фазовый переход первого рода описывается уравнением Клапейрона:
,
где
— удельная теплота фазового перехода, которая численно равна количеству теплоты сообщаемой единице массы вещества для осуществления фазового перехода,
— температура фазового перехода,
— изменение удельного объема при переходе

Клаузиус упростил уравнение Клапейрона для случаев испарения и возгонки, предположив, что

1. Пар подчиняется закону идеального газа
2. Удельный объем жидкости много меньше удельного объема пара

Из пункта один следует, что состояние пара можно описать уравнением Менделеева-Клапейрона
,
а из пункта два — что удельным объемом жидкости можно пренебречь.

Таким образом, уравнение Клапейрона принимает вид
,
где удельный объем можно выразить через
,
и окончательно

разделяя переменные, получим

Проинтегрировав левую часть от до , а правую от до , т.е. от одной точки до другой точки , лежащей на линии равновесия жидкость-пар, получим уравнение

называемое уравнением Клаузиуса-Клапейрона.

Собственно, это и есть искомая зависимость температуры кипения от давления.

Проведем еще пару преобразований

,
здесь
— молярная масса воды, 18 г/моль

— универсальная газовая постоянная, 8.31 Дж/(моль × К)

— удельная теплота испарения воды 2.3 × 10 6 Дж/кг

Теперь осталось установить зависимость атмосферного давления от высоты. Здесь мы воспользуемся барометрической формулой (другой у нас все равно нет):

или
,
здесь
— молярная масса воздуха, 29 г/моль
— универсальная газовая постоянная, 8.31 Дж/(моль×К)
— ускорение силы тяжести, 9.81 м/(с×с)
— температура воздуха

Значения, относящиеся к воздуху, пометим индексом v, к воде — h
Приравняв и избавившись от экспоненты, получим

На самом деле реальное давление воздуха не следует барометрической формуле, так как при больших перепадах высот температуру воздуха нельзя считать постоянной. Кроме того, ускорение свободного падения зависит от географической широты, а атмосферное давление — еще и от концентрации паров воды. То есть значение по этой формуле мы получим приближенное. Поэтому ниже я включил еще один калькулятор, который использует использует формулу для расчет температуры кипения в зависимости от давления воздуха в миллиметрах ртутного столба.

Калькулятор зависимости температуры кипения от высоты:

Источник

Барометрическое нивелирование

Калькулятор находит разность высот в зависимости от давления воздуха на первой и второй высоте и средней температуры воздуха.

Думаю, никто не станет возражать против заявления, что на высоте двух километров воздух более разрежен и атмосферное давление меньше, чем на высоте уровня моря.
Если же облечь эти слова в научную форму, то получится, что давление (плотность) газа зависит от его высоты в поле тяжести. На этом явлении построен метод барометрического нивелирования.

Барометрическое нивелирование — метод определения разности высот между двумя точками по измеряемому в этих точках атмосферному давлению. Так как атмосферное давление, помимо высоты над уровнем моря также зависит от погоды, например, от содержания в воздухе водяных паров, то метод применяется, если есть возможность провести измерения в точках с как можно более меньшим интервалом между измерениями, а сами точки расположены не слишком далеко друг от друга.

Разность высот рассчитывается по формулам.
Существует довольно сложная формула Лапласа:

Она, помимо температуры и давления, также учитывает абсолютную влажность воздуха и широту места измерения, то есть, ей на практике вроде бы и не пользуются.

А пользуются более простой формулой Бабинэ (Жак Бабинэ — французский физик, 1794-1872)
,
где — коэффициент расширения газов, равный

Собственно, в эпоху без компьютеров и калькуляторов даже эта формула была. ну, не сложной, но долгой в вычислениях, поэтому для определения разности высот пользовались вспомогательными таблицами барометрических ступеней.

Барометрическая ступень — высота, на которую надо подняться, чтобы давление понизилось на 1 мм.рт.ст.
То есть, взяли и упростили формулу Бабинэ до выражения

и рассчитали h для различных значений температуры и давления.
Получились таблицы, аналогичные Барометрическая ступень (м/мм.рт.ст)

Таким образом, измерив, например, разность давлений при средней температуре t и среднем давлении p, метеоролог мог найти значение барометрической ступени из таблицы, и умножить его на величину разности давлений.

Понятно, что формулы дают результат с погрешностью, но утверждается при этом, что погрешность не превышает 0,1 – 0,5 % от измеряемой высоты.

Метод барометрического нивелирования позволяет определить высоту точки над уровнем моря, не прибегая к геодезической нивелировке.
На практике, высоту точки над уровнем моря определяют используя ближайший репер, высота которого над уровнем моря известна.
Например, отметка репера 156 метров. Барометр у репера показывает 748 мм. рт. ст., будучи перенесен на определяемую точку, барометр показывает 751 мм. рт. ст. Средняя температура воздуха равна 15 градусов Цельсия. Используя формулу Бабинэ, получаем -33,78 м, то есть точка ниже репера на 33,78 метра, и имеет высоту примерно 122,22 м. Приняв за среднее давление 748 мм.рт.ст. и используя барометрические таблицы, получаем -33.85, то есть высоту примерно 122,15 м.

Калькулятор ниже иллюстрирует все вышесказанное.

Источник

Атмосферное давление

Собственный вес столба воздуха создает атмосферное давление, которое уменьшается по мере удаления от поверхности Земли.

Вблизи земной поверхности: При подъеме на каждые 8 м атмосферное давление падает на 100 Па = 1 мбар.

Если предположить, что температура воздуха с высотой не меняется, то атмосферное давление уменьшается с высотой по экспоненциальному закону.

p0	атмосферное давление у поверхности Земли,	Па
ph	атмосферное давление на высоте,	Па
h	высота над поверхностью Земли,	м
ρ0	плотность воздуха у поверхности Земли,	кг.м 3
g	ускорение свободного падения,	м/c 2
e	2.71828,

то для высот примерно до 100 км давление (при постоянной температуре) рассчитывается по формуле

Если давление у поверхности Земли p₀ = p_н = 101.325 кПа (до 1980 г. — 760 мм рт. ст.) и температура воздуха на любой высоте равна 0°С, то из формулы следует:

где высота h выражена в километрах.

Формула (1) называется барометрической формулой высоты. При точных вычислениях атмосферного давления следует учитывать понижение температуры воздуха по мере увеличения высоты.

При p_н = 101.325 кПа (среднегодовое значение атмосферного давления на уровне моря) и t = 15°С (среднегодовое значение температуры на уровне моря) для высот до 11 000 м (тропосфера) следует пользоваться международной формулой:

где давление выражено в килопаскалях, высота h — в километрах, или

где плотность выражена в кг/м 3 , высота — в километрах.

Атмосферное давление зависит от места измерения, температуры воздуха и погоды. На уровне моря среднегодовое атмосферное давление составляет p_н = 1013.25 мбар = 101,325 кПа (нормальное давление) при среднегодовой температуре 15°С.

Источник

Как с высотой изменяется атмосферное давление. Формула, график

Не все знают, что на разной высоте давление атмосферы отличается. Существует даже специальный прибор для измерения и давления, и высоты. Называется он барометр-альтиметр. В статье мы подробно изучим, как с высотой изменяется атмосферное давление и при чем тут плотность воздуха. Рассмотрим эту зависимость на примере графика.

Давление атмосферы на разных высотах

Атмосферное давление зависит от высоты. При ее увеличении на 12 м давление уменьшается на 1 мм ртутного столба. Этот факт можно записать с помощью такого математического выражения: ∆h/∆P=12 м/мм рт. ст. ∆h — это изменение высоты, ∆P — изменение атмосферного давления при изменении высоты на ∆h. Что из этого следует?

Из формулы видно, как с высотой изменяется атмосферное давление. Значит, если мы поднимемся на 12 м, то АД уменьшится на 12 мм ртутного столба, если на 24 м — то на 2 мм ртутного столба. Таким образом, измеряя атмосферное давление, можно судить о высоте.

Миллиметры ртутного столба и гектопаскали

В некоторых задачах давление выражается не в миллиметрах ртутного столба, а в паскалях или гектопаскалях. Запишем вышеприведенное соотношение для случая, когда давление выражено в гектопаскалях. 1 мм рт. ст. =133,3 Па =1,333 гПа.

Теперь выразим соотношение высоты и атмосферного давления не через миллиметры ртутного столба, а через гектопаскали. ∆h/∆P=12 м/1,333 гПа. После вычисления получим: ∆h/∆P=9 м/гПа. Выходит, что когда мы поднимаемся на 9 метров, то давление уменьшается на один гектопаскаль. Нормальное давление — это 1013 гПа. Округлим 1013 до 1000 и примем, что на поверхности Земли именно такое АД.

Если мы поднимаемся на 90 м, как с высотой изменяется атмосферное давление? Оно уменьшается на 10 гПа, на 90 м — на 100 гПа, на 900 м — на 1000 гПа. Если на земле давление в 1000 гПа, а мы поднялись на 900 м вверх, то атмосферное давление стало нулевым. Так что, получается что атмосфера заканчивается на девятикилометровой высоте? Нет. На такой высоте есть воздух, там летают самолеты. Так в чем же дело?

Связь плотности воздуха и высоты. Особенности

Как с высотой изменяется атмосферное давление вблизи поверхности Земли? На этот вопрос уже ответила картинка выше. Чем больше высота, тем меньше плотность воздуха. Покуда мы находимся недалеко от поверхности земли, изменение плотности воздуха незаметно. Поэтому на каждую единицу высоты давление уменьшается примерно на одно и тоже значение. Два записанные нами ранее выражения нужно воспринимать как правильные, только если мы находимся недалеко от поверхности Земли, не выше 1-1,5 км.

График, показывающий как атмосферное давление изменяется с высотой

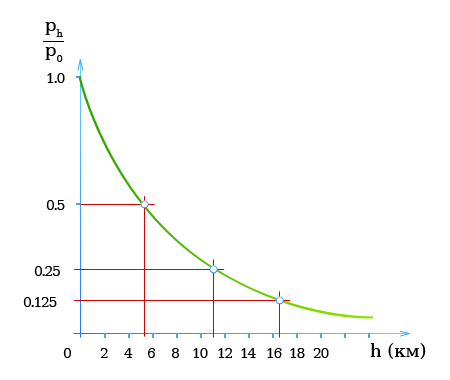
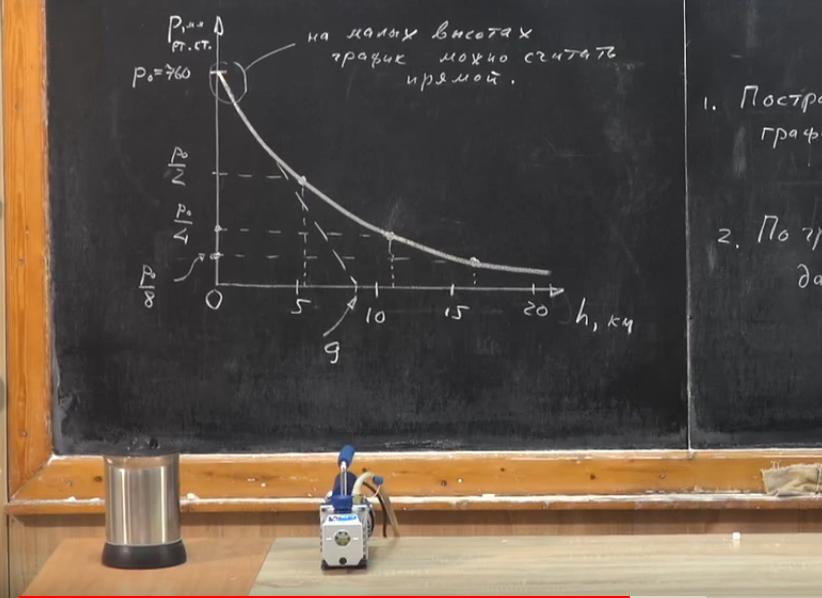
Теперь перейдем к наглядности. Построим график зависимости давления атмосферы от высоты. При нулевой высоте P₀=760мм рт. ст. Из-за того, что с ростом высоты давление уменьшается, атмосферный воздух будет менее сжат, его плотность станет меньше. Поэтому на графике зависимость давления от высоты не будет описываться прямой линией. Что это значит?

Как с высотой изменяется атмосферное давление? Над поверхностью земли? На высоте 5,5 км оно уменьшается в 2 раза (Р₀/2). Оказывается, что если мы поднимемся еще на такую же высоту, то есть на 11 км, давление уменьшится еще вдвое и будет равно Р₀/4 и т. д.

Соединим точки, и мы увидим, что график — это не прямая, а кривая. Почему, когда мы записывали соотношение зависимости, складывалось впечатление, что на высоте 9 км атмосфера заканчивается? Мы считали, что график является прямой на любых высотах. Это было бы так, если бы атмосфера была жидкой, то есть если бы ее плотность была постоянной.

Важно понимать, что этот график является лишь фрагментом зависимости на малых высотах. Ни на какой точке этой линии давление не снижается до нуля. Даже в глубоком космосе существуют молекулы газов, которые, правда, не имеют отношение к земной атмосфере. Ни в одной точке Вселенной не существует абсолютного вакуума, пустоты.

Источник