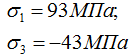11.10. Круги напряжений Мора
Удобное двумерное геометрическое представление трёхмерного напряжённого состояния было предложено немецким учёным О. Мором. Отнесём материальную частицу к главным осям (рис. 11.21). Рассечём её плоскостью, содержащей направление третьей главной оси (рис. 11.21,а). Тогда, согласно (11.35), имеем:
Уравнения (11.59) представляют собой параметрические уравнения окружности, каноническое уравнение которой имеет в системе координат вид (рис. 11.22):
Координаты центра окружности , радиус .
Окружность Мора позволяет графически найти напряжение на любой площадке, положение которой характеризуется углом Для этого нужно отложить по часовой стрелке угол и провести под этим углом радиус R до пересечения с окружностью в точке М. Координаты этой точки и есть искомое значения . Наибольшее касательное напряжение возникает при и равно численно радиусу окружности Мора:
Минимальное значение возникает на площадке при и равно:
Аналогичные круги Мора можно построить для наклонных площадок, содержащих главные направления 1 и 2 (рис. 11.23).
Их уравнения в параметрической форме имеют вид:
откуда следует, что наибольшее касательные напряжения в этих случаях:
также равны радиусам соответствующих кругов Мора.
носят название главных касательных напряжений. Они удовлетворяют тождеству
Каждой точке на любой из окружности Мора отвечают напряжения и площадки, направление которой характеризуется одним из углов Те площадки, которые не содержат ни одну из главных осей, окружностями Мора не описываются. Можно показать, что напряжения на этих площадках задаются точками, расположенными между окружностями в заштрихованной области. Из рис. 11.24 видно, что:
Следовательно, определяется радиусом большого круга Мора. Величину
называют параметром вида напряжённого состояния Лоде. При наложе-
нии на напряжённое состояние частицы всестороннего давления параметр Лоде не изменяется. Для одноосного растяжения имеем , для сжатия имеем , для плоского чистого сдвига . Соответствующие круги Мора приведены на рис. 11.25.
Таким образом, параметр Лоде характеризует вид напряжённого состояния.
Если изначально напряжённое состояние не является двухосным, связанным с главными осями, то для построения круга напряжений Мора при плоском напряжённом состоянии следует использовать формулы (11.35):
Поступая так же, как и в случае двухосного растяжения сводим пара-
метрические уравнения окружности (11.63) к каноническому виду
В (11.64) мы имеем более сложное выражение радиуса окружности:
При уравнение (11.64) сводится к (11.60) как частному случаю.
При построение круга Мора показано на рис. 11.26. Сначала определяется положение центра С круга как точки с координатами
Затем определяется положение точки А, характеризующей напряжения на грани х элемента при , т.е. . Здесь следует пом-
нить правило знаков для и других напряжений, указанных на
рис. 11.12. Заметим, что точки А и В, характеризующие напряжения на площадках, расположенных под углом 90 0 друг к другу, лежат на противо-
положных концах диаметра круга Мора. Далее на АВ с центром в точке С чертится круг. Напряжения на произвольной площадке, лежащей под углом к оси х, можно определить следующим образом. Отклады-
ваем от точки А по часовой стрелке угол и определяем положение точки М на круге с искомыми координатами . Точка М / , диаметра-
льно противоположная Д, даёт напряжения для площадки, состав-
ляющей угол 90 0 с той, которая имеет нормаль , т.е. для площадки с уг-
лом с осью х. Точка Д даёт максимальное касательное напряже-
ние, равное радиусу круга Мора:
Одной из важных задач использования круга Мора является определе-
ние главных нормальных напряжений и . Этим напряжениям отве-
чают точки Р1 и Р2 круга. Из рис. 11.26 следует, что угол между направле-
ниями на точки А и Р1 равен удвоенному углу , определяющему первое главное напряжение, а угол между направлениями А и Р2 – удвоенный угол , определяющий второе главное направление. Имеет место соотношение
которое совпадает с формулой (11.36).
Из изложенного следует, что круг Мора можно использовать в качес-
тве графического способа определения как напряжений на произвольной площадке, так и главных нормальных и максимальных касательных напря-
Источник
Решение плоской задачи о.К. Мора Прямая задача Мора
Прямая задача Мора – это задача определения напряжений на произвольной площадке по известным главным напряжениям. Рассмотрим элементарный объем, находящийся в условиях объемного напряженного состояния, причем грани этого объема являются главными площадками. Секущей площадкой, параллельной главному напряжению σ2, выделим из этого объема треугольную призму: 

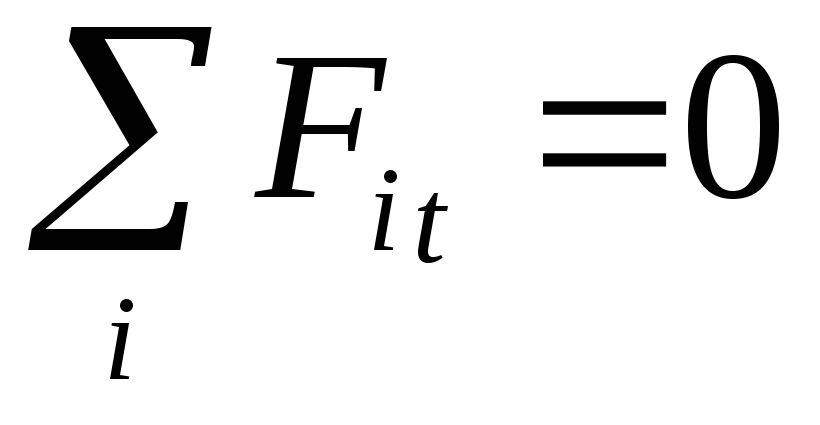










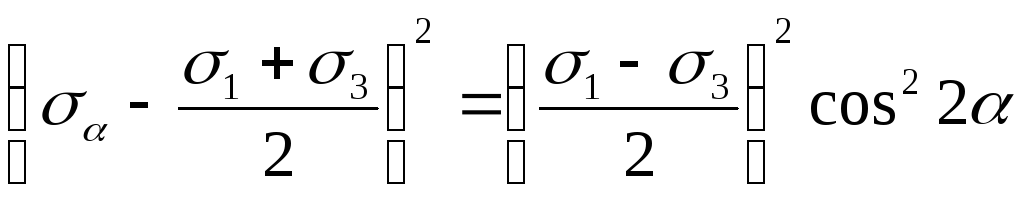











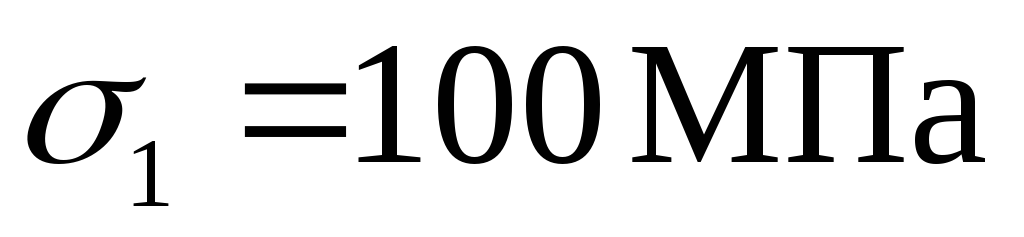




Обратная задача Мора
Обратная задача Мора состоит в определении главных напряжений по известным напряжениям на произвольной площадке. Рассмотрим её на конкретном примере. Задача. Определить главные напряжения в опасной точке стержня, подвергающегося совместному действию изгиба и кручения: 









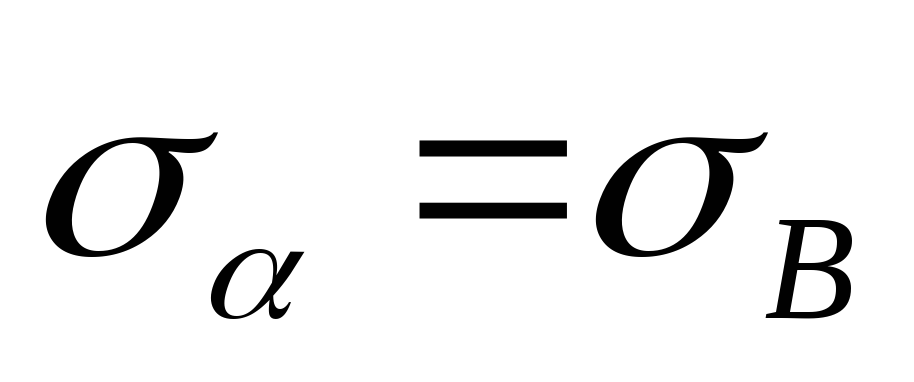


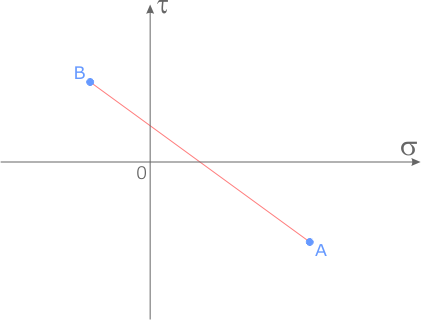
- В системе координат нанести точки с координатами
(,) и
(,). При этом нормальное напряжение считается положительным, если оно вызывает растяжение, а касательное – если оно действует по часовой стрелке относительно центра элемента.
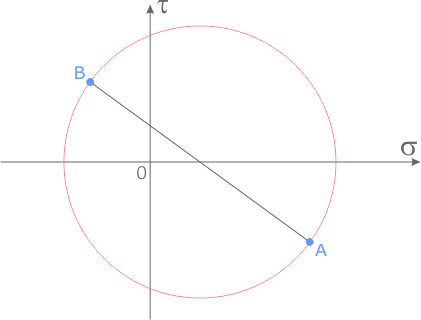
- Соединить полученные точки DиDотрезком. Точка пересечения этого отрезка с осью абсциссOявляется центром круга Мора.
- Построить окружность с центром в точке Oи радиусомOD. Координаты точек пересечения окружности с осью абсцисс дают величины главных напряжений (в нашем случае, и).
- Пересечение площадок (горизонталь) и(вертикаль) дает положение полюса площадок круга МораPпл(точка, в которой пересекаются все площадки).
- Провести из полюса Pпллучи через точки (, 0) и (, 0). Эти лучи задают положение главных площадок.

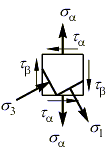
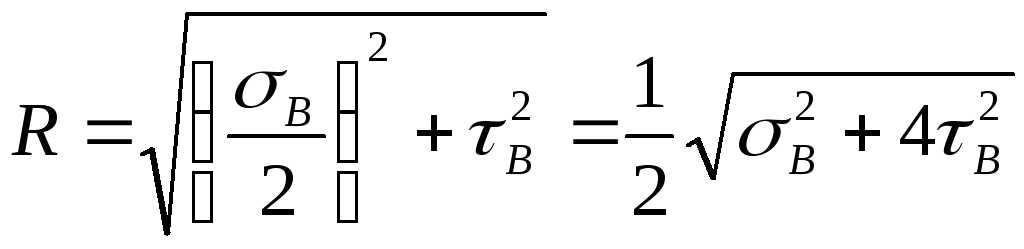


Источник
Определение главных напряжений по кругу Мора
Пример нахождения графическим способом по кругу Мора, величины и направления главных напряжений по известным нормальным и касательным напряжениям.
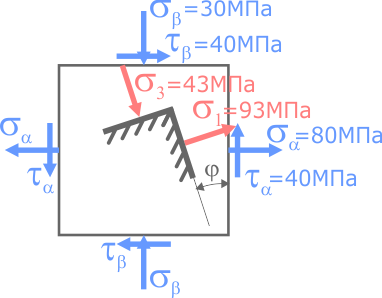
Определить величину, знак и направление главных напряжений с помощью круга Мора по заданным нормальным и касательным напряжениям на гранях элемента.
Пример решения
Предыдущий пункт решения задачи — построение круга Мора
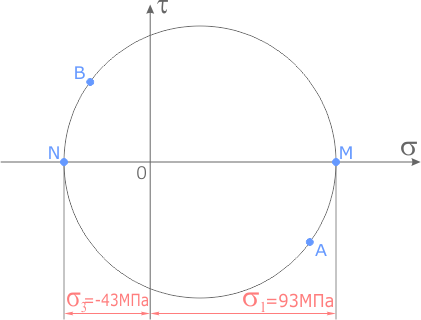
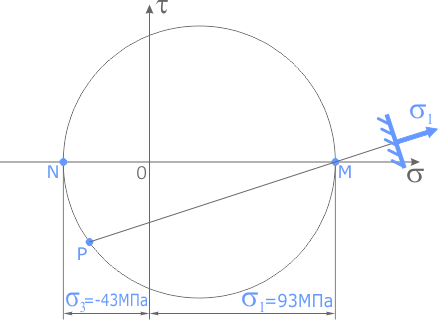
Как было показано ранее, координаты точек пересечения круга Мора с осью напряжений σ показывают величину главных напряжений.
В данном случае главные напряжения в точке элемента составляют
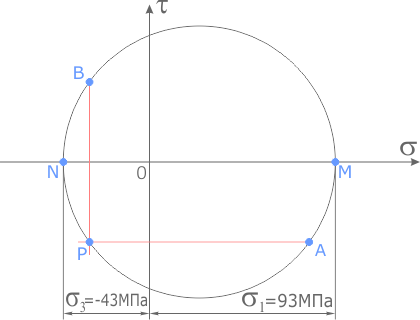
Для определения направления главных напряжений выполним следующие действия:
Из точки A проводим луч влево, а из точки B вниз до пересечения.
Точка их пересечения обозначается буквой P и является полюсом круга Мора. Очевидно, она будет располагаться на окружности.
Луч, проведенный из полюса через точку М, показывает направление главного напряжения σ 1.
Так как точка M расположена в области положительных значений σ то по правилу знаков соответствующее главное напряжение будет растягивающим (стрелка напряжения направляется от площадки).
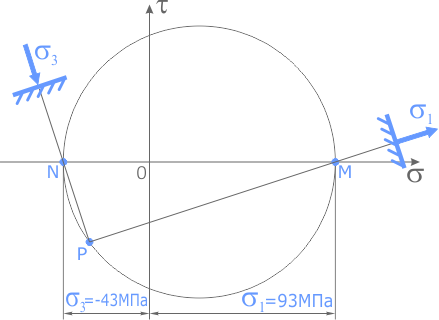
Аналогично, луч [PN) показывает направление главного напряжения на смежной площадке элемента.
Расположение точки N слева от пересечения осей σ — τ указывает на то, что это напряжение сжимающее (стрелка напряжения направлена в сторону площадки).
Покажем полученные напряжения на заданном элементе.
Для наглядности, главные площадки изображаются в пределах заданного элемента.
Здесь видно, что в сечении элемента расположенном под углом φ к начальному, касательные напряжения исчезают, а нормальные изменив величину, становятся главными.
Источник
Построение круга Мора
Пример построения круга Мора для плоского напряженного состояния элемента по заданным нормальным и касательным напряжениям.
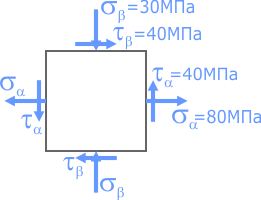
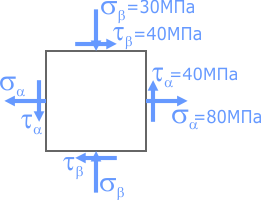
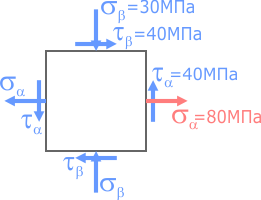
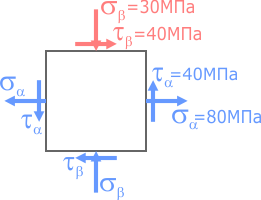
Построить круг Мора для случая плоского напряженного состояния, показанного на рисунке.
Известны направления и значения нормальных и касательных напряжений.
Круг Мора строится в плоской системе координат σ-τ .
Для построения круга потребуются нормальные и касательные напряжения с двух любых взаимно перпендикулярных площадок (например, правой и верхней) при этом ось σ системы направляется вдоль большего (с учетом знака) из нормальных напряжений.
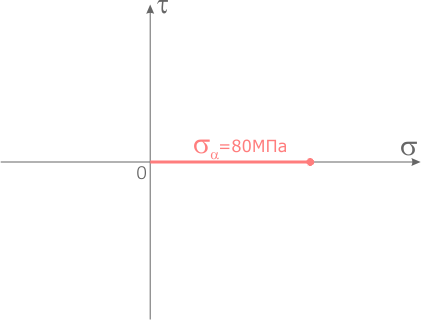
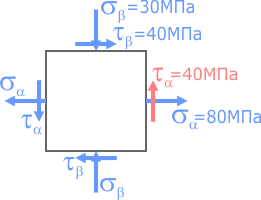
Начнем с правой площадки элемента.
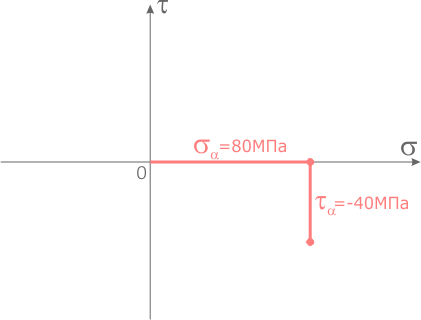
Из центра системы координат отложим вдоль оси σ значение соответствующего нормального напряжения σα =80МПа с учетом его знака.
Из конечной точки отрезка отложим вдоль оси τ значение соответствующего касательного напряжения τα =40МПа так же с учетом знака.
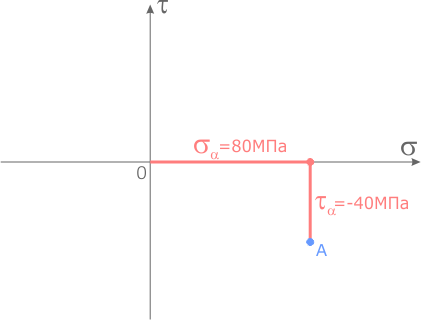
На конце последнего отрезка отметим точку, обозначив ее буквой A.
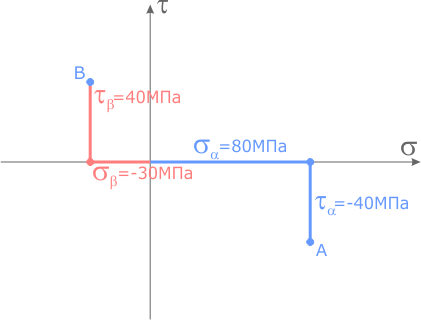
Аналогично для верхней площадки элемента.
Согласно закона парности касательных напряжений, точки A и B всегда будут расположены по разные стороны от оси σ и равноудалены от нее.
Для главных напряжений (при отсутствии касательных) точки A и B останутся на оси нормальных напряжений.
Полученные точки A и B соединяем отрезком.
На отрезке AB как на диаметре вычерчиваем окружность, с центром в точке пересечения отрезка AB с осью σ системы координат.
Множество точек полученной окружности показывают величину и знак нормальных и касательных напряжений при соответствующем положении площадок элемента.
Точки пересечения круга Мора с осью σ показывают величину и знаки главных напряжений.
Источник

 (,) и
(,) и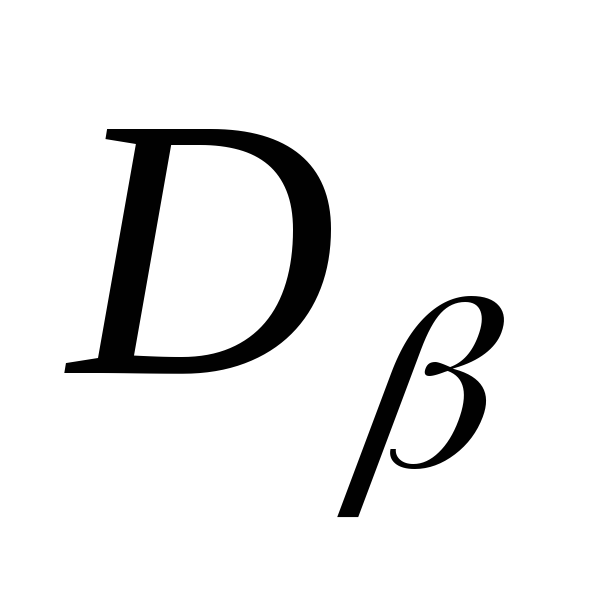 (,). При этом нормальное напряжение считается положительным, если оно вызывает растяжение, а касательное – если оно действует по часовой стрелке относительно центра элемента.
(,). При этом нормальное напряжение считается положительным, если оно вызывает растяжение, а касательное – если оно действует по часовой стрелке относительно центра элемента.