Как рассчитать давление бассейна

Как рассчитать давление бассейна

Если у меня есть бассейн размером 6x6x5 м (ширина × длина × высота в метрах) и я устанавливаю гипотетическую плитку размером 1×1 м на стене, каким будет давление воды для самой нижней плитки в кг / м2? То есть, какое давление нижняя часть плитки получает в кг / м2?

Цени любую помощь в расчете этого. Аппроксимация в порядке.

Давление — это просто сила, деленная на площадь.

Теперь вопрос в том, какова сила воды в бассейне? Это просто, это его плотность (в г / см 3 или умноженная на 1000 в кг / м 3 ) умноженная на гравитацию (в м / с 2 ) умноженная на высоту столб воды (в метрах). Единицы измерения: (кг мм) / (м 3 с 2 ) или (кг м / с 2 ) / (м 2 ), и мы знаем, что (кг м / с 2 ) называется ньютоном и обозначается как N. Итак, у нас есть N / m 2 , и это число выражается в ньютонах на квадратный метр. Этот блок также называется Паскаль и записывается как Па.

Так что Давление = (плотность) (сила тяжести) (высота)

Где у — высота бассейна

Итак, давайте вернемся к этому. Плотность воды составляет 997 кг / м 3 , плотность 9,81 м / с 2 , и вы говорите, что глубина воды в этом бассейне составляет 5 м.

Итак, Давление = (997 кг / м 3 ) (9,81 м / с 2 ) (5 м) = 48902,85 Н / м 2 = 48902,85 Па.

Теперь это в самом дне бассейна.

Так что по поводу сторон? Не все так просто, поскольку давление не является постоянной величиной, оно меняется с высотой (как мы видели ранее при P = ρgy)

Поэтому нам нужно исчисление, чтобы получить этот ответ. Представьте себе маленькую прямоугольную полоску области, которая проходит от одной стороны бассейна к другой.

Теперь давайте вернемся к тому, что давление. Давление = Сила / Площадь.

Сила тогда равна (давление) (площадь)

Таким образом, сила против стены в одной из маленьких полос вдоль стороны теперь равна: ∫dF = ∫P dA

Но помните, что давление всегда: P = ρgy

Итак, теперь у нас есть это: ∫dF = ∫ρgy dA

А что такое дА? Площадь небольшой прямоугольной полосы равна длине, умноженной на высоту, длину, которую мы будем хранить как L, а высота — это то, что может измениться (иди на давление на любой глубине на стороне бассейна), так что будет dy

Итак, теперь: ∫dF = ∫ρgyL dy

Видишь, куда это идет?

так что теперь у нас есть = pgL ∫y dy

И это действительно от y = ноль (дно пула) до y = h, который является высотой пула, какой бы она ни была.

Теперь давайте интегрируем это:

Где L — длина стороны, в вашем случае 6 метров, а y может быть любой высотой, которую вы хотите вдоль этой стены, в данном случае от 0 (низ) до 6 м (верх, когда бассейн заполнен водой) ,

Не обратите внимание, что L умножить на у равен площади стены.

И F / A = Давление

Поэтому, если бы я хотел узнать силу в самом низу, я бы сделал это:

F = 0,5 (997) (9,81) (6) (5 2) F = 733542,75 Н

Но ждать? Это не то, что мы получили раньше! Это потому, что раньше мы рассчитывали давление. Это сила. Чтобы получить давление в этой точке (снизу), просто разделите это на площадь. И, вероятно, также важно отметить, что сила воды на горизонтальных стенах действует как треугольник, вот так.

Таким образом, площадь этой силы составляет (6) (5) / 2 = 15 м 2

Поэтому, если мы разделим полученную нами силу (733542,75 Н) и поделим ее на 15 м 2 , мы получим: 48902,85 Н / м 2

То же самое Давление (Сила / Площадь), которое мы получили в первой части этой проблемы.

Большое спасибо за объяснение этого. Мне потребуется некоторое время, чтобы переварить это. Еще раз спасибо. очень признателен. Но что, если интересующая меня площадь составляет всего 1 м2 на нижней части боковой стены?

Если я прикреплю плитку размером 1 х 1 м на боковую стенку, какое давление воды получит эта единственная плитка из воды глубиной 5 метров?

Поскольку u / no_sponsor_pays_me, вероятно (и по понятным причинам) после этого исчерпывается, я добавлю, что сила на один квадратный метр — это давление в Н / м 2 , которое он дал как 48902,85. Н / м 2 умножить на один квадратный метр, или 48902,85 Н.

Вес в 1 кг притягивается силой тяжести, чтобы приложить 9,81 Н силы, поэтому это давление эквивалентно 48902,85 / 9,81 = 4985 кг. Если вы берете воду плотностью 1000 кг / м 3 , а не 997, получается 5 тонн.

Вот почему бассейны на верхних этажах зданий очень и очень дороги для последующей подгонки.

Спасибо за объяснение этого дальше. Очень признателен.

5 тонн, если для нижнего этажа бассейна справа, но как насчет самой нижней боковой стенки?

Почти столько же. Если вы на самом деле говорите о квадрате, по 1 метру с каждой стороны, то его средняя глубина составит всего 4,5 метра (верхний край имеет глубину 4 метра, нижний край имеет глубину 5 метров), поэтому сила будет эквивалентна только 4,5. тонн.

Понимаю. в этом есть смысл. Большое спасибо.

Источник

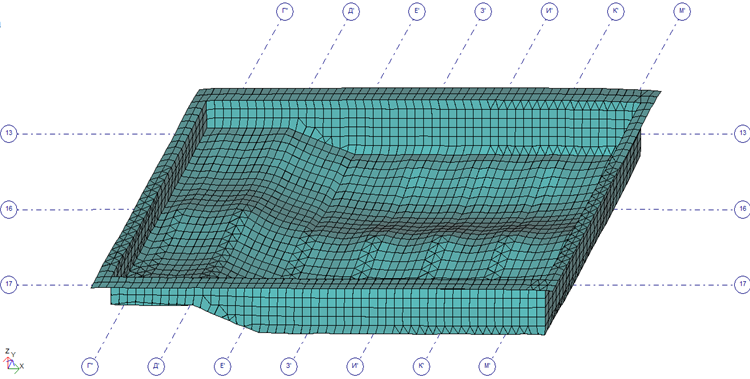
Расчет и конструирование монолитной железобетонной ванны бассейна. Геометрия конструкции, граничные условия , страница 2

На стенки ванны бассейна также воздействует нагрузка от гидростатического давления воды. Она моделируется равномерно распределенной треугольной нагрузкой с максимальным значением (нормативным):

— для «мелкой» части бассейна: 1,35 ∙ 10 = 13,5 кН/м 2

— для «глубокой» части бассейна: 2,85 ∙ 10 = 28,5 кН/м 2

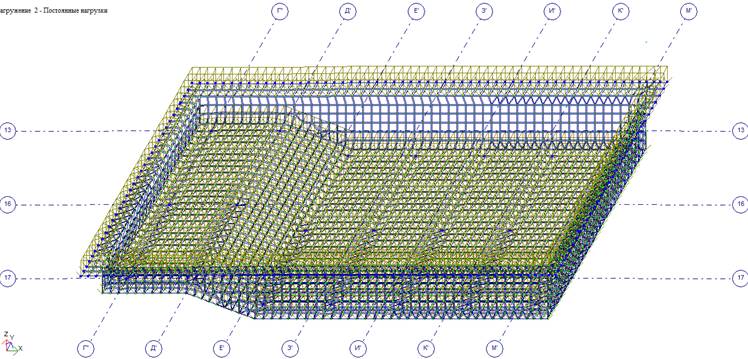
Загружение 2 — Постоянные нагрузки на дно и перекрытие

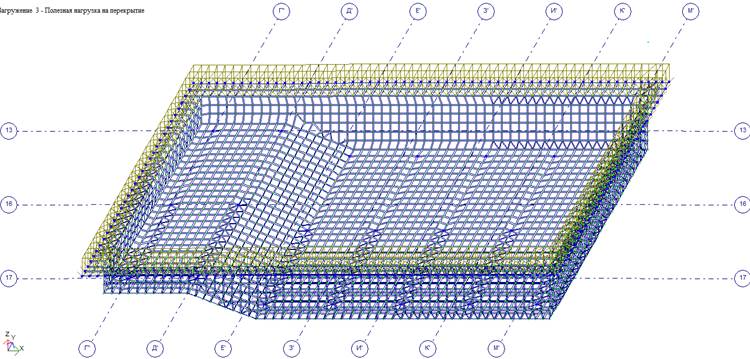
Загружение 3 — Полезная нагрузка на перекрытие

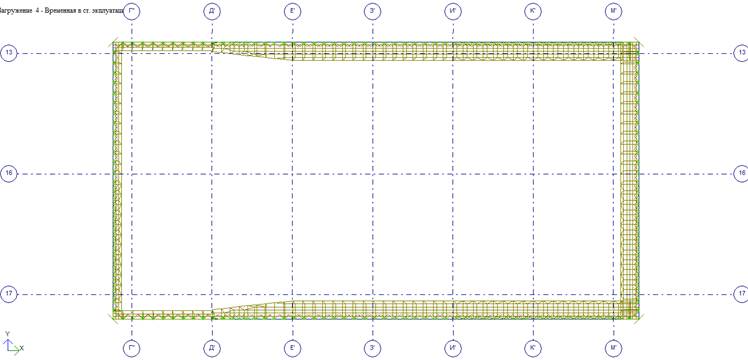
Загружение 4 — Временная нагрузка на ванну бассейна в период эксплуатации

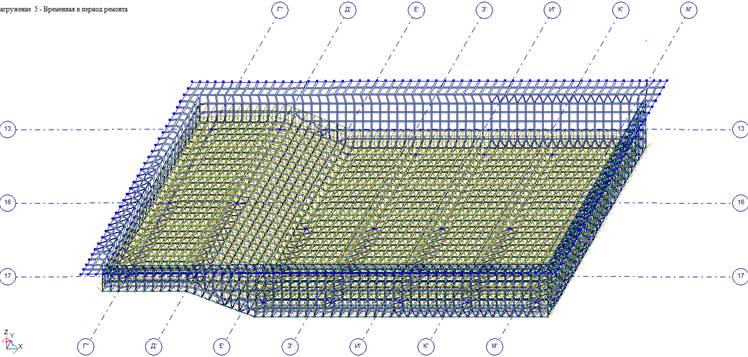
Загружение 5 — Временная нагрузка на ванну бассейна в период ремонта

Расчетные сочетания нагрузок

После загружения расчетной схемы определенными выше нагрузками, формируем расчетные сочетания нагрузок:

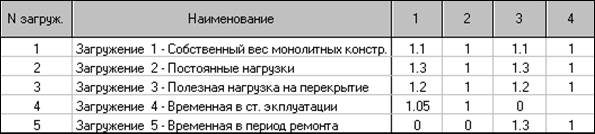
РСН-1: «Период эксплуатации» — расчетные нагрузки

— Загружение 1 — Собственный вес монолитных конструкций (γ_f = 1,1)

— Загружение 2 — Постоянные нагрузки (γ_f = 1,3)

— Загружение 3 — Полезная нагрузка на перекрытие (γ_f = 1,2)

— Загружение 4 — Временная нагрузка на ванны бассейна в период эксплуатации (γ_f = 1,05)

РСН-2: «Период эксплуатации» — нормативные нагрузки

— Загружение 1 — Собственный вес монолитных конструкций (γ_f = 1)

— Загружение 2 — Постоянные нагрузки (γ_f = 1)

— Загружение 3 — Полезная нагрузка на перекрытие (γ_f = 1)

— Загружение 4 — Временная нагрузка на ванны бассейна в период эксплуатации (γ_f = 1)

РСН-3: «Период ремонта» — расчетные нагрузки

— Загружение 1 — Собственный вес монолитных конструкций (γ_f = 1,1)

— Загружение 2 — Постоянные нагрузки (γ_f = 1,3)

— Загружение 3 — Полезная нагрузка на перекрытие (γ_f = 1,2)

— Загружение 5 — Временная нагрузка на ванны бассейна в период ремонта (γ_f = 1,3)

РСН-4: «Период ремонта» — нормативные нагрузки

— Загружение 1 — Собственный вес монолитных конструкций (γ_f = 1)

— Загружение 2 — Постоянные нагрузки (γ_f = 1)

— Загружение 3 — Полезная нагрузка на перекрытие (γ_f = 1)

— Загружение 5 — Временная нагрузка на ванны бассейна в период ремонта (γ_f = 1)

Таблица РСН в программном комплексе «ЛИРА»

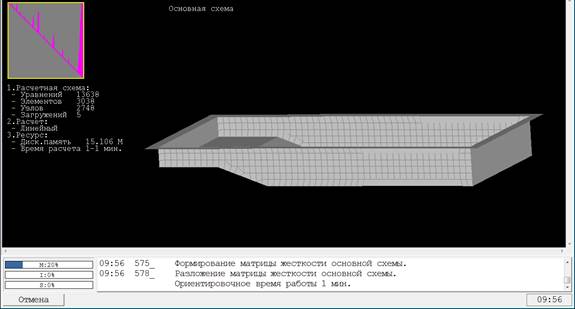
3. Статический расчет конструкции

Окно расчетного процессора модуля ЛИР-ВИЗОР

Деформированное состояние ванны бассейна

(масштаб перемещений многократно увеличен для наглядности)

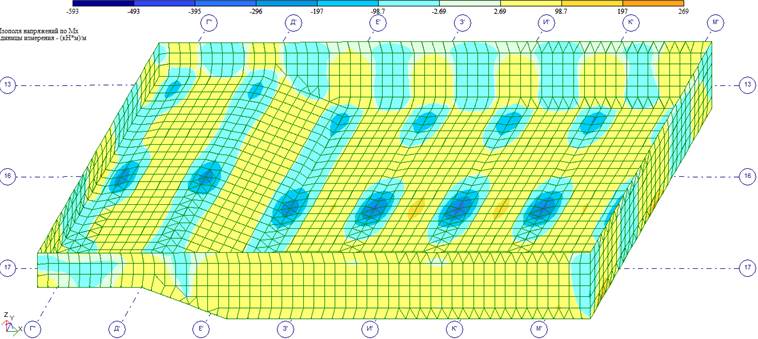
Изополя изгибающих моментов Мх от РСН-1

Изополя изгибающих моментов Мy от РСН-1

Изополя поперечных сил Qx от РСН-1

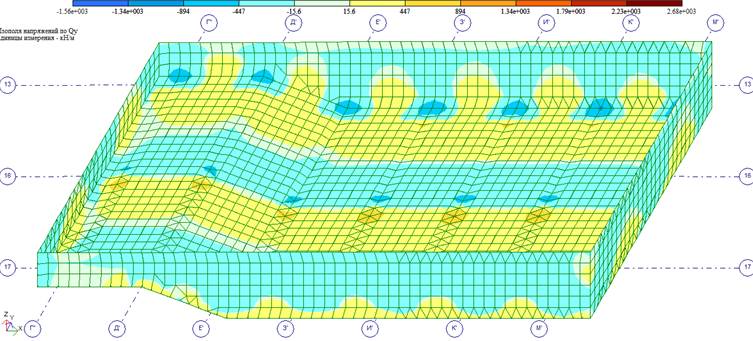
Изополя поперечных сил Qy от РСН-1

Далее, при экспорте расчетной схемы в конструирующий модуль для железобетонных конструкций ЛИР-АРМ, расчет армирования монолитных конструкций ванны бассейна будет произведен по усилиям, показанным на изополях, приведенных выше.

4. Расчет армирования монолитных конструкций

Прочностной расчет железобетонных элементов каркаса ведется по результатам статического расчета всей конструкции.

В конструирующий модуль «ЛИР-АРМ» заложены алгоритмы расчета железобетонных конструкций как по российским, так и по международным стандартам. Расчет ведем по СНиП 52-01-2003.

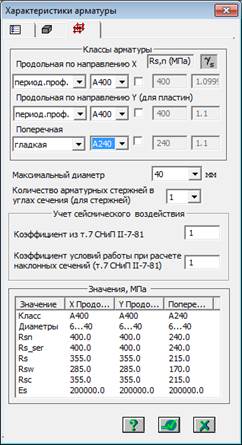
Для расчета монолитных конструкций ванны бассейна, необходимо задать дополнительные характеристики материалов – бетона и арматуры, а также модуль армирования.

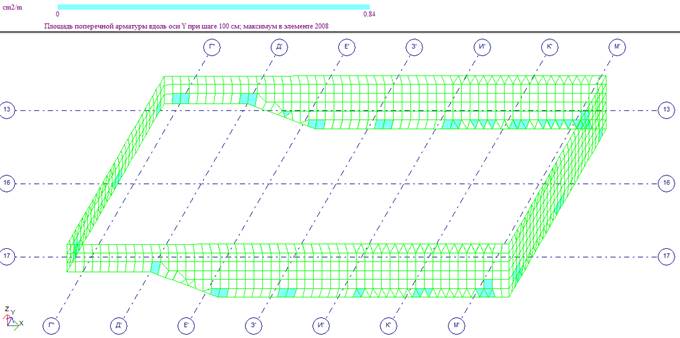
Ниже представлены мозаики армирования для элементов ванны бассейна, полученные после расчета конструкции по РСН.

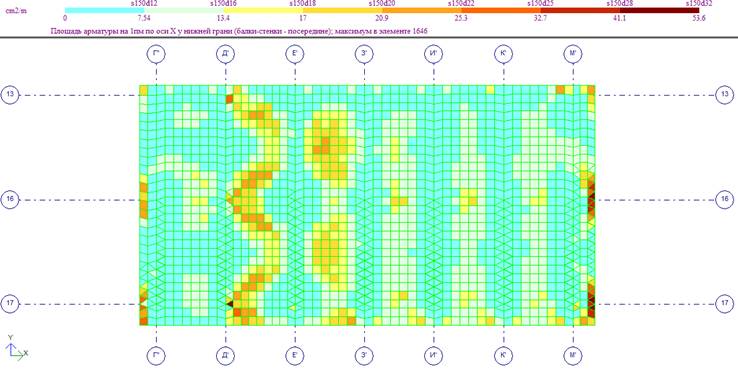
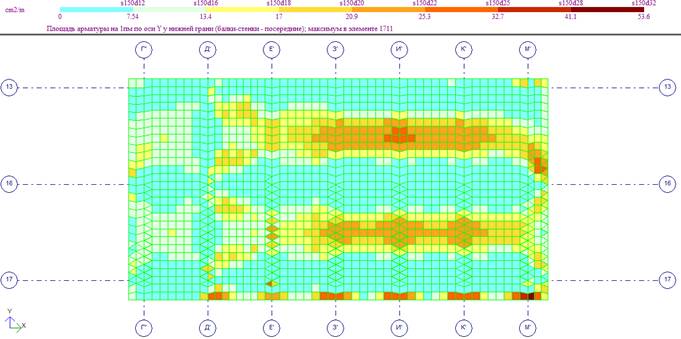
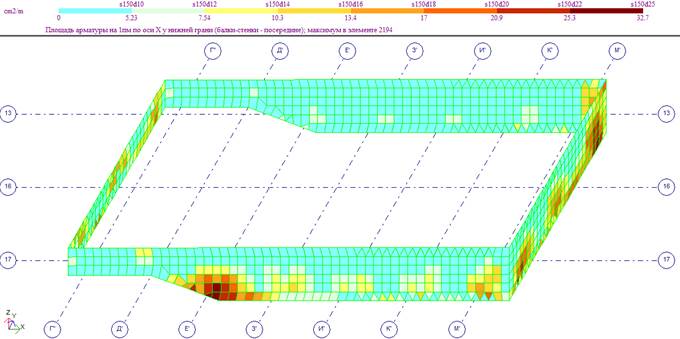
Продольное армирование нижней зоны днища по оси Х

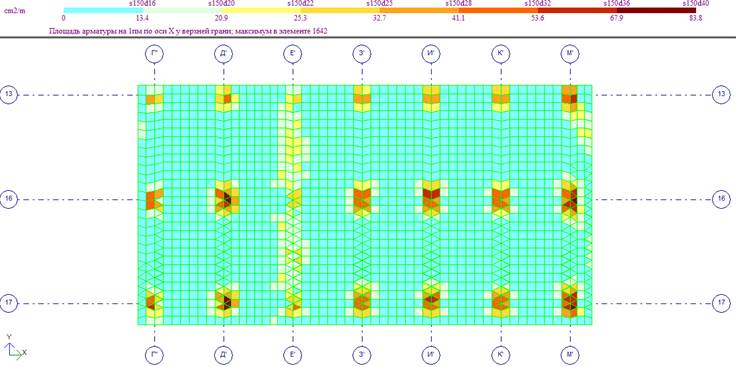
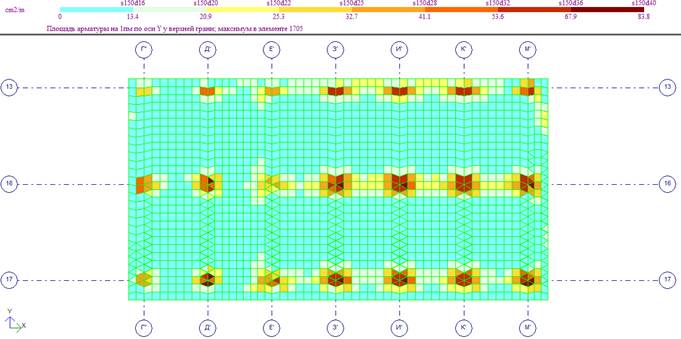
Продольное армирование верхней зоны днища по оси Х

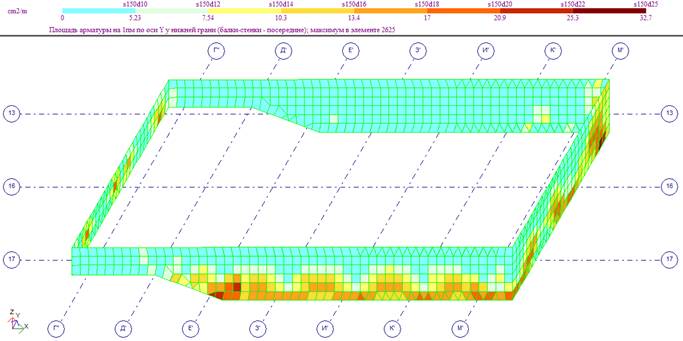
Продольное армирование нижней зоны днища по оси Y

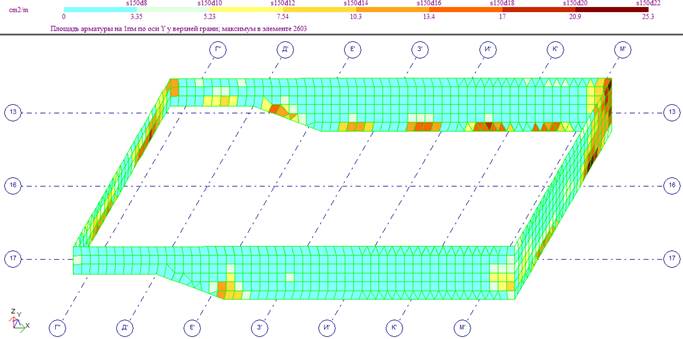
Продольное армирование верхней зоны днища по оси Y

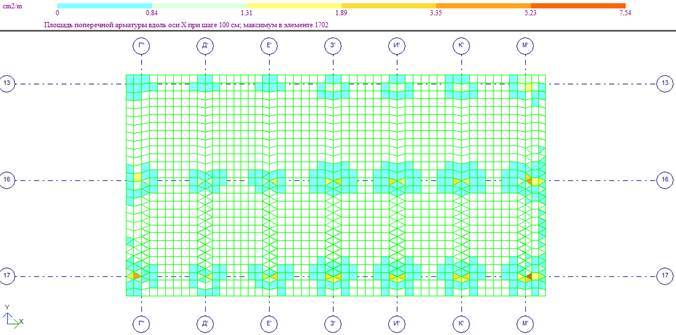
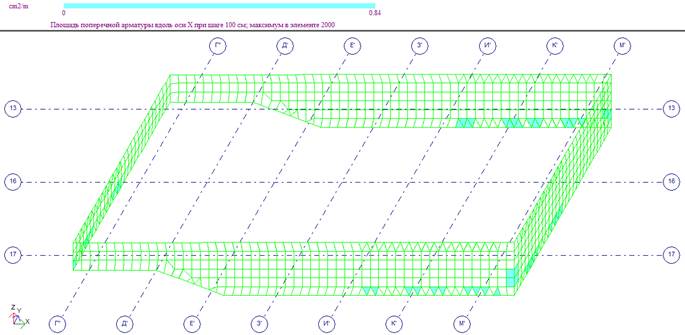
Поперечное армирование по оси X

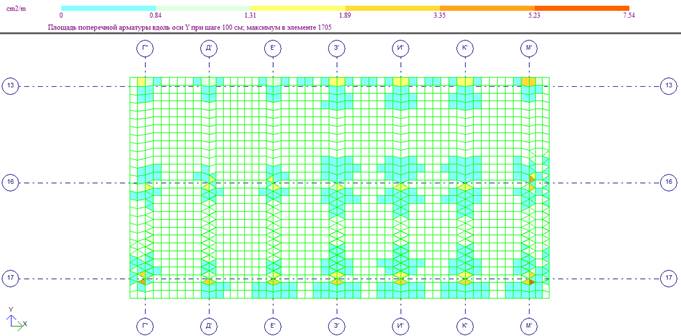
Поперечное армирование по оси Y

Продольное горизонтальное армирование наружной зоны стенок

Продольное горизонтальное армирование внутренней зоны стенок

Продольное вертикальное армирование наружной зоны стенок

Продольное вертикальное армирование внутренней зоны стенок

Поперечное армирование в горизонтальном направлении

Поперечное армирование в вертикальном направлении

Принимаем основную продольную арматуру днища и стенок ванны бассейна в виде стержней Ø25 А400 с шагом 150 мм в обоих направлениях.

В верхней зоне днища в опорной зоне колонн устанавливаем дополнительную продольную арматуру в виде стержней Ø20 А400 с шагом 150 мм в обоих направлениях на площади 2,1х2,1 м. Суммарный шаг арматурных стержней в этих местах — 75 мм.

В нижней зоне днища под стенкой по оси М’ устанавливаем также дополнительную арматуру в направлении оси Х в виде стержней Ø20 А400 с шагом 150 мм на ширину 1,5м. Стержни загибаем в стенки на 1 м.

Поперечное армирование принимаем в виде хомутов Ø12 А240 с шагом 150мм в обоих направлениях в опорной зоне колонн на площади 2,1х2,1м.

Источник

Гидростатическое давление

Калькулятор находит неизвестные величины по заданным, используя формулу давления столба жидкости.

Калькулятор ниже предназначен для расчета неизвестной величины по заданным, используя формулу давления столба жидкости.
Сама формула:

Калькулятор позволяет найти

• давление столба жидкости по известным плотности жидкости, высоте столба жидкости и ускорению свободного падения
• высоту столба жидкости по известным давлению жидкости, плотности жидкости и ускорению свободного падения
• плотность жидкости по известным давлению жидкости, высоте столба жидкости и ускорению свободного падения
• ускорение свободного падения по известным давлению жидкости, плотности жидкости и высоте столба жидкости

Вывод формул для всех случаев тривиален. Для плотности по умолчанию используется значение плотности воды, для ускорения свободного падения — земное ускорение, и для давления — величина равная давлению в одну атмосферу. Немного теории, как водится, под калькулятором.

Гидростатическое давление

Гидростатическое давление — давление столба воды над условным уровнем.

Формула гидростатического давления выводится достаточно просто

Из этой формулы видно, что давление не зависит от площади сосуда или его формы. Оно зависит только от плотности и высоты столба конкретной жидкости. Из чего следует, что, увеличив высоту сосуда, мы можем при небольшом объеме создать довольно высокое давление.
В 1648 г. это продемонстрировал Блез Паскаль. Он вставил в закрытую бочку, наполненную водой, узкую трубку и, поднявшись на балкон второго этажа, влил в эту трубку кружку воды. Из-за малой толщины трубки вода в ней поднялась до большой высоты, и давление в бочке увеличилось настолько, что крепления бочки не выдержали, и она треснула.

Также это приводит к такому явлению как гидростатический парадокс.

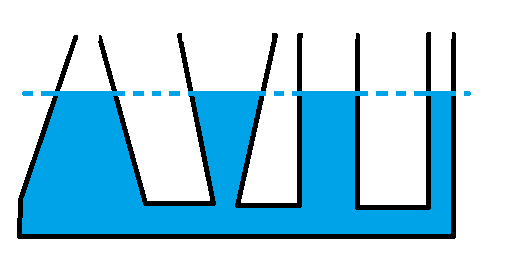
Гидростатический парадокс — явление, при котором сила весового давления налитой в сосуд жидкости на дно сосуда может отличаться от веса налитой жидкости. В сосудах с увеличивающимся кверху поперечным сечением сила давления на дно сосуда меньше веса жидкости, в сосудах с уменьшающимся кверху поперечным сечением сила давления на дно сосуда больше веса жидкости. Сила давления жидкости на дно сосуда равно весу жидкости лишь для сосуда цилиндрической формы.

На картинке вверху давление на дно сосуда по всех случаях одинакова и не зависит от веса налитой жидкости, а только от ее уровня. Причина гидростатического парадокса состоит в том, что жидкость давит не только на дно, но и на стенки сосуда. Давление жидкости на наклонные стенки имеет вертикальную составляющую. В расширяющемся кверху сосуде она направлена вниз, в сужающемся кверху сосуде она направлена вверх. Вес жидкости в сосуде будет равен сумме вертикальных составляющих давления жидкости по всей внутренней площади сосуда

Источник