Как работают сообщающиеся сосуды фонтан

Сообщающиеся сосуды

Тебе не раз приходилось пользоваться кофейником, чайником и садовой лейкой, но вряд ли ты знал, что эти предметы являются сообщающимися сосудами.

Сообщающиеся сосуды — это любые емкости, соединенные между собой. Самый простой пример сообщающихся сосудов — это две трубочки, которые соединены между собой резиновым шлангом.

Сообщающиеся сосуды в быту

Если у тебя дома есть стеклянный заварочный чайник, ты можешь наблюдать следующую картину. Если ты наклоняешь чайник, чай начинает выливаться тогда, когда доходит до края носика, при этом чай в носике и в самом чайнике находится на одном горизонтальном уровне, как бы ты чайник ни наклонял.

Главное правило сообщающихся сосудов

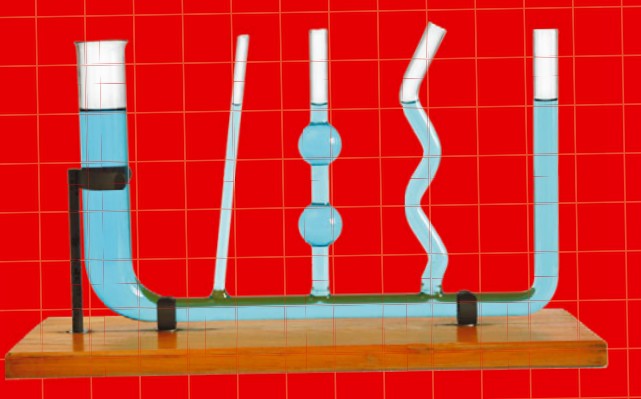
Неважно, какое количество сосудов соединены между собой — уровень жидкости во всех сосудах будет одинаковым. Более того, форма сосудов также не оказывает влияния на уровень жидкости.

Главное правило сообщающихся сосудов заключается в том, что уровни жидкости в них устанавливаются на одной высоте.

Однако это правило распространяется только на однородные жидкости. Если, например, в сосуд налить сначала воду, а потом масло, то жидкость в сообщающихся сосудах будет находиться на разных уровнях. В случае разных жидкостей все зависит от их плотности. Чем больше плотность, тем ниже уровень жидкости в одной из частей (колен) сообщающегося сосуда.

Что происходит в нашем организме, когда мы пьем? Как жидкость попадает к нам в рот? Оказывается, здесь наш организм работает по принципу сообщающихся сосудов. Когда мы хотим пить, мы открываем рот и подносим к нему стакан или бутылку с водой. В этот момент воздух во рту разрежается, легкие расширяются, и жидкость устремляется туда, где давление меньше.

Поэтому мы смело можем сказать, что мы пьем не только ртом, но и легкими.

По принципу сообщающихся сосудов устроены шлюзы на каналах и реках для прохождения судов. Шлюзовые камеры соединены подводным каналом. Когда подводный канал открывается, обе камеры становятся сообщающимися сосудами. При этом вода перетекает из камеры с высоким уровнем в камеру с низким. Как только уровень жидкости в обеих шлюзовых камерах выравнивается, ворота открываются, и судно может перемещаться из одной камеры в другую.

Артезианская скважина

Более сложный пример сообщающихся сосудов — артезианская скважина. Если скважину бурят в середине артезианского бассейна, то вода поднимается на поверхность земли по принципу сообщающихся сосудов.

Водонапорная башня

Водонапорная башня — еще один пример работы принципа сообщающихся сосудов. Бак для накопления воды устанавливается на большой высоте. От бака вниз идет множество труб в дома и квартиры каждого из нас. И когда мы открываем кран, то вода начинает течь.

Фонтан

Уникальные фонтаны Петергофа также являются сообщающимися сосудами. Уникальными их можно считать только лишь потому, что вода поднимается на довольно большую высоту без использования насосов. Это стало возможным благодаря учету уровней воды в каналах и фонтанах.

Источник

Закон сообщающихся сосудов и его применение.

Сообщающиеся сосуды – это сосуды, соединенные между собой ниже уровня жидкости в каждом из сосудов. Таким образом жидкость может перемещаться из одного сосуда в другой.

Перед тем как понять принцип действия сообщающихся сосудов и варианты их использования необходимо определиться в понятиях, а точнее разобраться с основным уравнением гидростатики.

Содержание статьи

Закон сообщающихся сосудов

Итак, сообщающиеся сосуды имеют одно общее дно и закон о сообщающихся сосудах гласит:

Какую бы форму не имели такие сосуды, на поверхности однородных жидкостей в состоянии покоя на одном уровне действует одинаковое давление.

Для иллюстрации этого закона и возможностей его применения начнем с рассмотрения основного уравнения гидростатики.

Основное уравнение гидростатики

где P1 – это среднее давление на верхний торец призмы,
P – давление на нижний торец,
g – ускорение свободного падения,
h – глубина погружения призмы под свободной поверхностью жидкости.

ρgh – сила тяжести (вес призмы).

Звучит уравнение так:

Давление на поверхность жидкости, произведенное внешними силами, передается в жидкости одинаково во всех направлениях.

Из написанного выше уравнения следует, что если давление, например в верхней точке изменится на какую-то величину ΔР, то на такую же величину изменится давление в любой другой точке жидкости

Доказательство закона сообщающихся сосудов

Возвращаемся к разговору про сообщающиеся сосуды.

Предположим, что имеются два сообщающихся сосуда А и В, заполненные различными жидкостями с плотностями ρ1 и ρ2. Будем считать, что в общем случае сосуды закрыты и давления на свободных поверхностях жидкости в них соответственно равны P1 и P2.

Пусть поверхностью раздела жидкостей будет поверхность ab в сосуде А и слой жидкости в этом сосуде равен h1. Определим в заданных условиях уровень воды в сообщающихся сосудах – начнем с сосуда В.

Гидростатическое давление в плоскости ab, в соответствии с уравнение гидростатики

если определять его, исходя из известного давления P1 на поверхность жидкости в сосуде А.

Это давление можно определить следующим образом

где h2 – искомая глубина нагружения поверхности ab под уровнем жидкости в сосуде В. Отсюда выводим условие для определения величины h2

P1 + ρ1gh1 = P2 + ρ2gh2

В частном случае, когда сосуды открыты (двление на свободной поверхности равно атмосферному), а следовательно P1 = P2 = Pатм , имеем

т.е. закон сообщающихся сосудов состоит в следующем.

В сообщающихся сосудах при одинаковом давлении на свободных поверхностях высоты жидкостей, отсчитываемые от поверхности раздела, обратно пропорциональны плотностям жидкостей.

Свойства сообщающихся сосудов

Если уровень в сосудах одинаковый, то жидкость одинаково давит на стенки обоих сосудов. А можно ли изменить уровень жидкости в одном из сосудов.

Можно. С помощью перегородки. Перегородка, установленная между сосудами перекроет сообщение. Далее доливая жидкость в один из сосудов мы создаем так называемый подпор – давление столба жидкости.

Если затем убрать перегородку, то жидкость начнет перетекать в тот сосуд где её уровень ниже до тех пор пока высота жидкости в обоих сосудах не станет одинаковой.

В быту этот принцип используется например в водонапорной башне. Наполняя водой высокую башню в ней создают подпор. Затем открывают вентили, расположенные на нижнем этаже и вода устремляется по трубопроводам в каждый подключенный к водоснабжению дом.

Приборы основанные на законе сообщающихся сосудов

На принципе сообщающихся сосудов основано устройство очень простого прибора для определения плотности жидкости. Этот прибор представляет собой два сообщающихся сосуда – две вертикальные стеклянные трубки А и В, соединенные между собой изогнутым коленом С. Одна из вертикальных трубок заполняется исследуемой жидкостью, а другая жидкостью известной плотности ρ1 (например водой), причем в таких количествах, чтобы уровни жидкости в среднем колене находились на одной и той же отметке прибора 0.

Затем измеряют высоты стояния жидкостей в трубках над этой отметкой h1 и h2. И имея ввиду, что эти высоты обратно пропорциональны плотностям легко находят плотность исследуемой жидкости.

В случае, когда оба сосуде заполнены одной и той же жидкостью – высоты, на которые поднимется жидкость в сообщающихся сосудах, будут одинаковы. На этом принципе основано устройство так называемого водометного стекла А. Его применяют для определения уровня жидкости в закрытых сосудах, например резервуарах, паровых котлах и т.д.

Принцип сообщающихся сосудов заложен в основе ряда других приборов, предназначенных для измерения давления.

Применение сообщающихся сосудов

Простейшим прибором жидкостного типа является пьезометр, измеряющий давление в жидкости высотой столба той же жидкости.

Пьезометр представляет собой стеклянную трубку небольшого диаметра (обычно не более 5 мм), открытую с одного конца и вторым концом присоединяемую к сосуду, в котором измеряется давление.

Высота поднятия жидкости в пьезометрической трубке – так называемая пьезометрическая высота – характеризует избыточное давление в сосуде и может служить мерой для определения его величины.

Пьезометр – очень чувствительный и точный прибор, но он удобен только для измерения небольших давлений. При больших давлениях трубка пьезометра получается очень длинной, что усложняет измерения.

В этом случае используют жидкостные манометры, в которых давление уравновешивается не жидкостью, которой может быть вода в сообщающихся сосудах, а жидкостью большей плотности. Обычно такой жидкостью выступает ртуть.

Так как плотность ртути в 13,6 раз больше плотности воды и при измерении одних и тех же давлений трубка ртутного манометра оказывается значительно короче пьезометрической трубки и сам прибор получается компактнее.

В случае если необходимо измерить не давление в сосуде, а разность давлений в двух сосудах или, например, в двух точках жидкости в одном и том же сосуде применяют дифференциальные манометры.

Сообщающиеся сосуды находят применение в водяных и ртутных приборах жидкостного типа, но ограничиваются областью сравнительно небольших давлений – в основном они применяются в лабораториях, где ценятся благодаря своей простоте и высокой точности.

Когда необходимо измерить большое давление применяются приборы основанные на механических принципах. Наиболее распространенный из них – пружинный манометр. Под действием давления пружина манометра частично распрямляется и посредством зубчатого механизма приводит в движение стрелку, по отклонению которой на циферблате показана величина давления.

Видео по теме

Ещё одним устройством использующим принцип сообщающихся сосудов хорошо знакомым автолюбителем является гидравлический пресс(домкрат). Конструктивно он состоит из двух цилиндров: одного большого, другого маленького. При воздействии на поршень малого цилиндра на большой передается усилие во столько раз большего давления во сколько площадь большого поршня больше площади малого.

Источник

Как работают сообщающиеся сосуды фонтан

Обоснование выбора данной темы

Однажды на уроке физики наш класс проходил принцип сообщающихся сосудов. В качестве домашнего задания нам предложили создать собственную модель. В тот момент мы вспомнили про фонтан «Дружбы Народов», находящийся на ВДНХ. Тогда мы решили подробно разобраться в работе фонтанов, а потом создать свою собственную модель.

Фонтаны это не только украшение, но и интересный физический механизм, о работе которого многие люди и не задумывались. Поэтому для нас важно рассказать и показать принцип работы такого интересного предмета, как фонтан.

Целью работы является исследование работы принципа сообщающихся сосудов, использующегося при работе фонтанов.

Для достижения заданной цели необходимо решить следующие задачи:

узнать, что собой представляет фонтан;

изучить принцип работы;

разобраться в истории фонтанов: от истоков к XXI веку;

узнать о самых известных примерах;

выполнить практическую часть работы.

Что такое фонтан

Каждый из нас видел фонтаны. Они бывают и комнатные, и садовые, и встроенные в ландшафт, и целые монументальные произведения искусства. Но не каждый задумывался, как появились фонтаны и как они работают.

Само слово фонтан произошло от латинского f ontana, что означает «источник», «струя», «родничок». Обычно видим только верхнюю, красивую часть, через которую и выплескивается вода. Но что же скрыто внутри?

А внутри мы увидим примитивный принцип сообщающихся сосудов, известный нам еще со школьных времен.

Принцип сообщающихся сосудов

Мы знаем, что в сообщающихся сосудах уровень жидкости одинаковой плотности устанавливается на одном уровне. Это и есть закон сообщающихся сосудов.

Доказать это мы можем таким образом:

из закона Паскаля мы можем узнать, что p 1= p 2, где p 1=ρ gh 1, p 2=ρ gh 2,следовательно, ρ gh 1=ρ gh 2, т.е. h 1= h 2, где p -давление в жидкости, а h -высота столба.

А в сообщающихся сосудах с жидкостями, разной плотности, высота столба с меньшей плотностью будет больше высоты столба с большей плотностью.

Доказываем тоже при помощи закона Паскаля.

где p -давление в жидкости, а h -высота столба.

Высоты столбов в сообщающихся сосудах с разнородными жидкостями обратно пропорциональны их плотностям.

История использования сообщающихся сосудов

Впервые принцип сообщающихся сосудов начал использоваться еще в Древней Греции. Это были небольшие фонтанчики, но служили они не для эстетического удовольствия, а для удаления жажды, охлаждения и освежения воздуха. Они создавались при помощи бурения земли до подводных рек и ключей при естественных перепадах высот. Позже эти перепады начали создаваться искусственно.

Понятие акведук происходит от латинских слов aqua — вода и ducere — вести . Акведуки являются прототипом современного водопровода. Они доставляли воду до общественных купальниц, называемых термами, Навмахий — мест римских водных сражений, богатых домов и фонтанов, о которых позже и пойдет речь. Особенностью римских водопроводов являлось то, что строители, древние римляне, не достаточно хорошо знали о принципе сообщающихся сосудов, поэтому строили их всё время под небольшим наклоном вниз, хотя этого и не требовалось. Достаточно было построить хранилище выше всех тех мест, куда должна была поступать вода.

В общей сложности насчитывалось около 11 таких величественных сооружений. Практически все они хорошо сохранились до наших дней. Это, несомненно, говорит о том, что римляне были просто гениальными инженерами и строителями.

3.2 Фонтаны в Средневековье и Новом Времени

Основой фонтанов в Средневековой Европе послужили персидские сады. Мусульманские фонтаны были окружены террасами из разноцветной плитки. Брызги, отражаясь в них, представали перед зрителями необыкновенной картиной. В Европе же сады впервые появились при монастырях. В их середине был расположен фонтан-место для уединения, размышления, молитвы. Но в большинстве фонтаны еще использовались как источники воды для полива и питья.

Наибольшего расцвета ландшафтное искусство в области фонтанов достигло в XVII веке во Франции. Лучший пример-Версаль, расположенный в 17 километрах от Парижа. Это парк фонтанов и архитектурных шедевров. Здесь находятся более 25 фонтанов, разных не только внешним оформлением, но устройством подачи воды.

Фонтаны-шутихи — еще одно произведение фонтанного искусства, появившееся еще за полторы тысячи лет до нашей эры. Но широкое распространение получили такие забавные фонтаны только в XVII в Европе.

Первые европейские шутихи не имели собственного стиля и создавались по арабо-сицилийским мотивам. Первый такой фонтан появился в парке «Эдем» в Бургундии, Франция.

На данный момент наиболее известны фонтаны-шутихи Петра I . Их прообразом могли служить фонтаны в Хелльбрунне под Зальцбургом.

Смысл таких фонтанов в придании игривого настроения среди посетителей парка при помощи неожиданного поливания водой. Часто такие фонтаны замаскированы под обыденные предметы, что и добавляет потешности .

3.4 Фонтаны нашего времени

В наше время фонтаны из маленьких отверстий для питья превратились в огромные и сложные системы. Если раньше маленькие фонтаны, созданные руками человека, считались чудом света, то сейчас каких только видов нет: с музыкой, с подсветкой, танцующие и т.д. Самый мощный фонтан выдает струю высотой до 318 метров (высота Эйфелевой башни 300)!

Фонтаны блещут разнообразием. Каждый из них это произведение искусства. Кто-то впечатляет размерами, а кто-то красотой подачи воды. В этой работе можно проследить, как происходила их эволюция.

4. Самые известные фонтаны мира

Изучив множество фонтанов в процессе изучения данной темы, мы решили составить собственный список самых красивых и удивительных фонтанов мира.

Светозвуковой фонтан на Кипре. Этот фонтан находится в небольшом курортном городке Протарас. Пусть это и не самый крупный и знаменитый фонтан, но его лазерные шоу просто впечатляют свой красотой и оригинальностью.

Фонтан Треви в Риме, Италия. Этот фонтан знаменит на весть мир. Его основная особенность — скульптурная композиция Нептуна с нимфами.

Фонтан короля Фахда. Этот фонтан расположен в Саудовской Аравии. Это тот самый высокий фонтан, про который мы говорили ранее. Напомним, что высота столба, выбрасываемого им, равна 318 метрам!

Фонтан «Белладжио». Этот фонтан построен на берегу искусственного озера в Лас-Вегасе. Есть обычай делать предложение, стоя рядом с этим фонтаном. В этом случае он будет олицетворять красоту любви.

Это танцующий фонтан. Ночью он подсвечивается десятками прожекторов, а его струю поднимаются более чем на 80 метров и переливаются всеми цветами радуги.

И, конечно, не забудем про фонтан, из-за которого и зародилась идея создания этого проекта.

Фонтан «Дружбы Народов» в Москве. Этот фонтан был построен еще в 1954 году, в качестве символа единства Советского союза. Огромный размер, роскошные позолоченные статуи, олицетворяющие различные республики. Для нас этот фонтан является самым красивым и роскошным из всех.

5. Практическая часть

Изучив простейший принцип работы фонтанов, мы захотели создать свою собственную модель. Для этого нам потребовалось:

фанера для декорации;

ракушки для украшения;

Сначала мы придумали идею декорации фонтана. Наш выбор остановился на доме с садом.

Для исполнения идеи мы вырезали из фанеры необходимые детали: фасад дома, заднюю крышку и подставку. Потом мы сделали сами сообщающиеся сосуды из бутылки и резиновой трубочки. Насадку подсоединили к сосудам и замаскировали ракушками, сымитировав с помощью железной коробки наружную часть фонтана.

В конце мы соединили все детали с помощью шурупов, петель и магнитов. Для завершения работы нам осталось только раскрасить нашу модель.

В процессе изучения данной темы мы смогли доказать верность закона сообщающихся сосудов, узнать о различных способах его применения, выяснить, где и для чего впервые использовались свойства данного утверждения. Также мы смогли проследить эволюцию развития фонтанного искусства, его виды и ответвления, узнать впечатляющие факты.

Но самым главным нашим достижением мы считаем собственноручно сделанную модель фонтана, с помощью которой мы можем продемонстрировать механизм для подачи воды.

Анализ результатов, полученных в ходе данной работы, позволяет сделать выводы:

принцип сообщающихся сосудов оказался хорошо применим в современном мире;

история использования этого принципа берет начало еще в Древней Греции и тянется до наших дней;

фонтанное искусство неотъемлемо связано с простейшей физикой;

посмотреть принцип работы фонтана можно даже в домашних условиях;

собственноручно можно создать работающую модель фонтана.

Источник