Как найти периметр дна бассейна

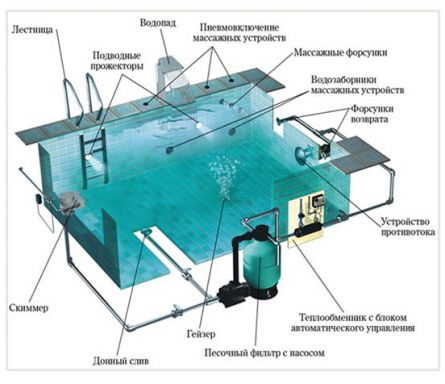
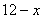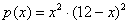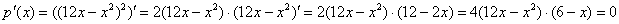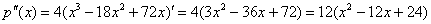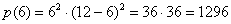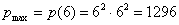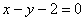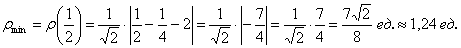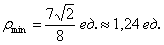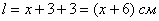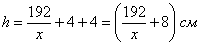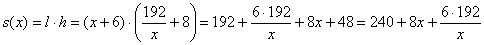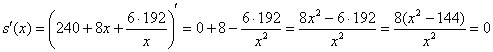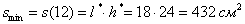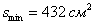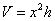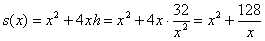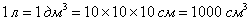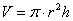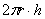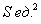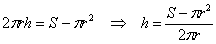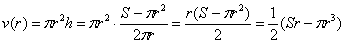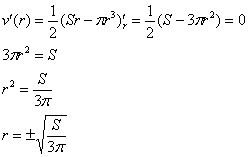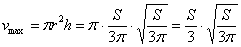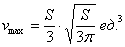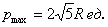БАССЕЙНЫ

Бетонный бассейн: сам рассчитал, сам построил

6. Гидроизоляция бассейна.

Для отделки и гидроизоляции бассейна существуют такие способы:

На данном этапе осуществляют монтаж технологического оборудования к которому относится: оборудование для нагрева воды, светотехническое оборудование, оборудование химической обработки воды, лестница, очистительная техника, монтаж труб от закладных элементов до технического помещения, которое будет обслуживать бассейн, для данного вопроса просто необходимо приглашать профессионалов.

В список обязательного оборудования для бассейна входит:

1. фильтровальная установка. Фильтровальные установки для бассейнов различаются по производительности(для больших и малых бассейнов), качеству материала, из которого изготовлен корпус фильтра и характеристикам самого фильтрующего материала(фильтры с полиэстером, фильтры с полипропиленом, фильтры с песочной засыпкой).
2. оборудование для подогрева воды. Подогрев бассейнов осуществляется при помощи электронагревателей (проточный нагреватель для бассейна с электрическим теплоносителем и проточный водонагреватель бассейна, использующий в качестве теплоносителя тепловой контур ) и теплоообменников(подключается к котлу дома).
3. устройства для забора и подачи воды — скиммеры (забор воды из бассейна и подача ее в фильтровальное устройство, а также сбор крупных загрязнений с поверхности воды),
4. форсунки возвратные,
5. донные сливы(для слива воды, бывают из пластика и нержавеющей стали)
6. лестницы для бассейнов в основном выполнены из полированной нержавеющей стали.
7. управление водоподготовкой, существует для осуществления контроля за нормальной работой подогрева, подсветки воды и водных аттракционов.

Также существует необязательное оборудование к которому относят: противоток (создает поток искусственного течения), ионизаторы воздуха (очищают воздух), водные аттракционы, подводное освещение и т. д.

Испытание бассейна. После окончания работ по изготовлению чаши бассейна нужно провести гидрологические испытания, то есть наполнить водой. Перед началом испытаний необходимо тщательным образом заглушить все выводы трубопроводов, чтоб вода не уходила через них. После того как чаша будет заполнена за ней наблюдают от 3 до 5 дней. Для этого ставят на стенках метки о уровне воды и следят нет ли утечек с внешней стороны чаши. При это следует помнить что испаряемость воды в среднем 1.5 л в сутки. В случае обнаружения локальных протечек их нужно устранить при помощи все тех же гидроизоляционных материалов(необходимо при помощи латки из ПВХ мембраны устранить протечку), если же уровень воды не менялся и визуально протечек не обнаружено, воду спускают, высушивают чашу. После этого выполняют обратную засыпку пазух котлована, желательно это делать песком средней крупности (с послойным уплотнением) или, в крайнем случае, непучинистым грунтом. При правильном уплотнении песка, осадки грунта по периметру бассейна не произойдет. Благоустройство прилегающих территорий Самый приятный, завершающий этап строительства. Для облагораживания «прибрежной» территории можно использовать камень, плитку, доску, газон, разного рода растения, небольшие кустарники и т. д. Край (борт бассейна) отделывается камнем, для того, чтоб закрыть примыкание пленки к каркасу и убрать не эстетичный вид краев чаши. Дальше все зависит от Вашей фантазии. К примеру, можно сделать дощатый настил вокруг бассейна на ширину 2-3 метра по периметру или же засеять газоном и посадить несколько вечнозеленых кустов или небольших деревьев, кое-где выложив каменные дорожки. Стоимость и сроки строительства бассейна. Цена и продолжительность строительства бассейна зависит от размеров и типа бассейна, типа применяемого оборудования, наличие специального оборудования (подводные аттракционы, горки, подводных светильников, устройство искусственного течения, гидромассажа или аэромассажа, водопадов). В стоимость бассейна можно включить такие пункты: Проектирование чаши бассейна в специализирующихся фирмах от 10-20 долларов за кв.м. Срок исполнения от 2 недель. Строительство чаши бассейна с материалами стоит от 150 долларов за квадратный метр. Срок исполнения от 1месяца, в зависимости от размеров и сложности. Гидроизоляция ПВХ мембраной от 50 долларов с работой за квадратный метр. Срок исполнения от 2 недель, в зависимости от конфигурации бассейна. Гидроизоляция из специальных растворов с отделкой мозаикой от 100 долларов с работой за квадратный метр. Оборудование: — фильтровальные установки от 300 евро — скиммеры и возвратные форсунки от 100 евро — донные сливы от 20 евро — насосы от 250 евро — электронагреватели от 450 евро — системы противотока от 1500 евро — освещение от 70 евро за светильник — лестницы от 200 евро. Все приведенные в статье цены работ и оборудования являются ориентировочными и служат целью определения масштаба стоимости общего строительства бассейна. Приведенный перечень оборудования не является окончательным. Бассейн готов. Теперь помимо купания и отдыха, необходимо тщательным образом следить за состоянием воды, мыть периодически стенки и дно бассейна, следить за тем, чтоб не образовывалось микроорганизмов, чтобы не засорялась система фильтрации, правильно эксплуатировать зимой и т.д. Все это можете делать Вы при помощи специальных химических составов и дополнительного оборудования либо же доверится профессиональным фирмам, которые занимаются обслуживанием бассейнов. Источник: www.builderclub.com

Источник

Расчет бассейна: вода, объем, стоимость

Инструкция к онлайн калькулятору расчета бассейна

Значения ключевых параметров Вашего будущего бассейна указывайте в миллиметрах.

X – внутренняя длина бассейна, определяется исходя из назначения бассейна (например: купальный, плавательный, лечебно-оздоровительный, декоративный), а также наличия свободного места для размещения на участке.

Y – внутренняя ширина бассейна, определяется с учетом Ваших пожеланий и отведенного для сооружения бассейна места на участке. Не забудьте предусмотреть место вокруг бассейна для зоны отдыха. Также следует размещать бассейн подальше от больших деревьев, поскольку их корневая система может постепенно разрушать гидроизоляционный слой, а листья будут падать в емкость, что потребует регулярного очищения воды. Однако СП 31-113-2004 «Бассейны для плавания» рекомендует при устройстве открытых бассейнов площади отведенного участка озеленять не менее чем на 35%, по периметру участка предусмотреть ветро- и пылезащитные полосы древесных и кустарниковых насаждений.

W – уровень воды в бассейне, это расстояние от поверхности воды до дна. Этот параметр очень важен. Если в бассейне будут купаться дети, водоем должен быть глубиной до 1000 мм. Для комфортного купания взрослых достаточно глубины 1500 мм. Сооружение более глубокого бассейна оправдано, при использовании горок и трамплинов. Для домашнего использования лучше строить резервуар со ступенчатыми глубинами, отдельную детскую и взрослую площадки.

H – высота стенки слева – геометрический размер от верхней плоскости левого бортика до дна бассейна.

H2 – высота стенки справа – подобно предыдущему параметру это расстояние от верхней плоскости бортика справа до дна бассейна.

Если дно бассейна плоское, то есть глубина воды по периметру бассейна одинакова, введите одно и то же число для H и H2.

Подход к бассейну должен располагаться со стороны мелкой зоны.

A – толщина стен – напрямую зависит от габаритов будущей конструкции, не менее 100 мм, поскольку должна выдержать давление воды с одной стороны и грунта с другой.

B – толщина дна, этот важный геометрический параметр следует определять исходя из качества грунта и уровня грунтовых вод, а также глубины бассейна. Чем глубже он будет, тем больший вес воды будет давить на 1 м 2 дна бассейна, поэтому толщину дна следует выбирать не менее 200 мм. Выбирая толщину стен и дна бассейна, следует руководствоваться СНиП 2.03.01-84 «Бетонные и железобетонные конструкции».

E – ширина бортика, то есть возвышения по периметру бассейна. Бортик необходим для защиты от попадания загрязняющих веществ из окружающего пространства в бассейн. При ширине свыше 400 мм – может быть так же использован для прохода по нему, сидения и лежания на нем при условии облицовки бортика не скользкими материалами.

F – высота бортика примерно 50-300 мм. Чтобы было удобно стоять у бортика, положив на него руки, а на них подбородок (для людей разного роста).

Функция «Дно с уступом» позволяет задать параметры уступа, если он планируется.

U1 – расстояние до уступа, чем больше это значение, тем дальше от входа в бассейн находится уступ.

U2 – ширина уступа, этот параметр определяет насколько пологим будет уступ.

Что можно посчитать при помощи данного калькулятора

Стенки бассейна.Вы также получите пример расчета стенок для строителства бетонного бассейна.

С помощью данного калькулятора вы можете подсчитать

Источник

Разметка плавательного бассейна

Стандарт бассейнов для спортивного плавания — 25 и 50 метров, ширина от 11,4 до 25 метров в зависимости от количества дорожек, глубина от 1,2 до 6 метров в зависимости от назначения бассейна, ширина дорожки от 2,25 до 2,5 метров.

Плавательные бассейны длиной 25 и 50 метров разделены на дорожки (как правило, их четное количество) разноцветными канатами-разделителями, закрепленными на крючки на обеих торцевых стенках бассейна . Разделители дорожек (волногасители) предназначены для того, чтобы организовать движение в бассейне, упростить ориентирование в воде и гасить волны. Волногасители состоят из поплавков диаметром от 5 до 15 см, плотно соединенных друг с другом по всей длине с помощью троса. Цвет поплавков на протяжении 5 метров от торцевых стенок бассейна должен чётко отличаться от цвета остальных поплавков.

В глубоких бассейнах на глубине не менее 1,2 метра ниже уровня воды вдоль стенок должны располагаться уступы для отдыха шириной 10-15 см.

Согласно стандартам, многие бассейны оборудованы стартовыми тумбочками, высотой 50-75 см над уровнем воды, с минимальным размером верхней площадки — 50 * 50 см, с них пловцы прыгают в воду при старте кролем, брассом и баттерфляем. Стартовые тумбочки должны быть твёрдыми и не обладать пружинящими свойствами, поверхность тумбочки не должна быть скользкой. Конструкция тумбочки должна позволять пловцу при старте захватывать руками края тумбочки спереди или с боков.

Максимальный наклон верхней площадки не должен быть более 10°. Та часть бассейна, где установлены стартовые тумбы, должна быть глубже, чтобы пловцы не задевали дно во время прыжка в воду.

Для старта при плавании на спине параллельны торцевым стенкам должны быть установлены горизонтальные и вертикальные ручки (поручни) на высоте 30-60 см над уровнем воды. Стартовые поручни не должны выступать за поверхность стенки.

Наряду с разделителями дорожек, пловцам помогает двигаться прямолинейно и придерживаться своей стороны разметка на дне спортивного бассейна. Посередине каждой дорожки прочерчены линии темного цвета, контрастирующего с цветом дна бассейна. Эти осевые линии имеют ширину 20-30 см, и заканчиваются в 2 метрах от торцевой стенки перпендикулярной линией длиной 1 метр той же ширины (получается как бы буква Т). «Буква Т» помогает рассчитать поворот при плавании на груди.

В бассейнах, где проводятся соревнования, на торцевых стенках бассейна или на контактных панелях должны быть нанесены линии цели, проходящие в центре торца каждой дорожки. Ширина этой линии такая же, как и у осевой линии на дне бассейна, 20-30 см. Линии на вертикальных стенках идут непрерывно от края ванны до дна и на глубине 30 см ниже уровня воды пересекаются под прямым углом линией длиной 50 см.

Поперек ванны бассейна, на расстоянии 5 метров от начала и конца дорожки и на высоте минимум 1,8- 2,5 метра от поверхности воды, подвешиваются два шнура с флажками, предназначенные для спортсменов, плывущих способом на спине, чтобы они могли видеть близость стенки и подготовиться к повороту. Также за 5 метров до конца дорожки меняется цветовая разметка на ограничителе дорожек (волногасителе).

Источник

Экстремальные задачи с производной

Совершенно верно, иногда от таких задач действительно захватывает дух. Сегодня на уроке мы разберём ещё одно важное приложение производной, имеющее самое что ни на есть прикладное значение! Речь пойдёт о задачах с конкретным геометрическим, физическим, экономическим и т.д. содержанием, в которых исходя из условия, нужно самостоятельно составить функцию и найти её точку минимума либо максимума (и/или, соответственно, минимум либо максимум).

Для полноценного изучения урока необходимо уметь находить производные, ПОНИМАТЬ, что такое производная и быть знакомым с понятиями возрастания, убывания и экстремума функции. Таким образом, начинающим рекомендую начать с вышеуказанных статей, чтобы не словить здесь реальный экстрим =) А уже заматеревшие студенты не должны испытать особых трудностей. Разминочная алгебраическая задача и новый материал по ходу решения:

Известно, что сумма двух положительных чисел равна 12. Какими должны быть эти числа, чтобы произведение их квадратов было максимальным?

Решение: прежде всего, хорошо осознаем, что от нас требуется: в условии фигурируют два положительных числа, причём ни то, ни другое мы не знаем. Но вот их сумма равна 12.

Если это, например, 2 и 10, то произведение квадратов ;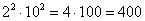
если 7 и 5, то 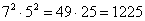и т.д.

И нам нужно отыскать такую пару, для которой данное произведение будет наибольшим. Понятно, что с методом подбора тут замучаешься, к тому же искомые числа ведь могут оказаться и дробными. Поэтому привлечём на помощь могучий аппарат математического анализа.

Но сначала вспомним школу и вспомним, как, наивно хлопая ресницами, мы что-то обозначали за «икс»…. Обозначим за 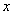одно из чисел. Тогда второе число будет равно:

Проверим, что их сумма действительно равна 12:
– а ведь и правду говорят, что всё гениальное просто =)

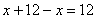
Теперь составим функцию произведения их квадратов:

Многие читатели уже понимают последующие шаги: далее нужно найти производную, критические точки и обнаружить точку (и), в которой функция 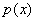достигает максимума (если таковые, конечно, вообще существуют).

И небольшой вопрос техники: производную здесь можно найти несколькими способами. На мой взгляд, удобен следующий вариант: загоняем множители под единую степень и раскрываем там скобки: 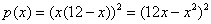, после чего дифференцируем сложную функцию:

Итак, 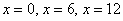– критические точки.

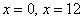
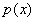
По условию оба числа положительны, поэтому значения сразу исключаем из рассмотрения. Осталось проверить достаточное условие экстремума для точки и выяснить, достигает ли там функция минимума либо максимума. А может статься, и ничего не достигает.

Проверка вам хорошо знакома: чертим числовую ось, выясняем знаки производной слева и справа от точки 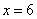и выносим вердикт. Так решать можно, и это будет правильным решением, но есть и другой путь!

Второе достаточное условие экстремума

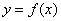
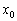
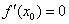
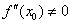
Пусть производная функции равна нулю в критической точке :
и пусть там существует вторая ненулевая производная: . Тогда:

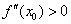
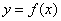
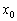
если , то функция достигает минимума в точке ;
если 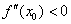, то – максимума.

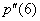
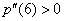
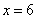
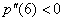
В нашем случае нужно найти вторую производную и вычислить – если окажется, что , то является точкой минимума; если же – то точкой максимума.

Для удобства дифференцирования утрамбуем предшественницу:
и незамедлительно оценим это удобство:

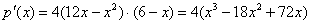
Подставим критическое значение :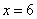
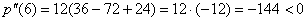
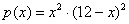
, значит, функция достигает максимума в данной точке:

Ответ: искомые числа: 6 и 6, при этом максимальное произведение квадратов:

Вообще говоря, по условию не требовалось находить само произведение, но по правилам хорошо тона его лучше рассчитать и указать в ответе. К тому же это весьма любопытно.

На практике в подавляющем большинстве случаев встречаются задачи с геометрическим смыслом, и поэтому основная часть урока будет посвящена именно им. Начнём с несложного типового примера, который почему-то довольно часто вызывает проблемы:

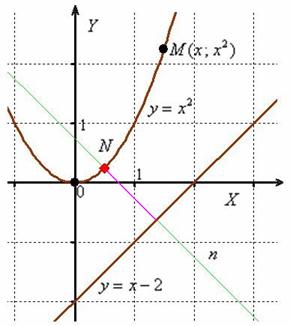
Найти наименьшее расстояние между параболой 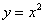и прямой

Решение: вот, пожалуйста, самый что ни на есть практический смысл – представьте, что вам нужно пройти от дороги к дороге. Совершенно понятно, что в отсутствии препятствий это наиболее выгодно осуществить по кратчайшему пути.

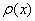
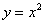
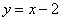
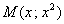
Поскольку условие запрашивает наименьшее расстояние, то, очевидно, нам нужно составить функцию расстояния между параболой и прямой . За аргумент этой функции принимаем абсциссу точки , которая принадлежит параболе и «свободно перемещается по ней»:

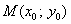
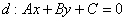
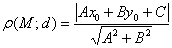
Используем формулу расстояния от точки до прямой :

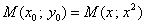
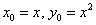
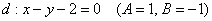
В нашем случае (т.е. );
.

Таким образом:
– функция расстояния между параболой и прямой, зависящая от абсциссы точки параболы.

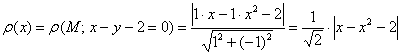
Дифференцируем по обычным правилам, невзирая на модуль: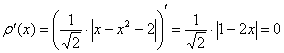

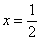
– критическая точка

Проверим выполнение достаточного условия экстремума. Оцените, насколько второе достаточное условие приятнее и удобнее 1-го:
для всех «икс». В частности:
, следовательно, функция достигает минимума в точке :

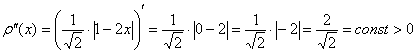
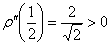
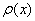
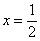
Искомая «дорога» изображена малиновым отрезком на чертеже.

Ответ:

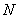
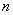
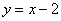
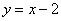
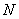
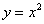
Физики в лирике могут найти ординату точки , уравнение нормали и её точку пересечения с прямой . Кстати, почему кратчайший путь проходит именно по нормали? Приложите ребро ладони к прямой и начните плавно сдвигать его к параболе: первая точка, которой вы коснётесь – будет в точности точка , ваша рука займёт положение касательной к графику функции в данной точке, а расстояние между двумя прямыми как раз и определится малиновым отрезком нормальной прямой.

Следующая задача для самостоятельного решения:

Из куска проволоки длиной 30 см требуется согнуть прямоугольник наибольшей площади. Каковы размеры этого прямоугольника?

Давайте немного проанализируем условие:

Что требуется найти? Очевидно, длину и ширину – это «традиционные» характеристики, определяющие прямоугольник.

Какую функцию нужно составить? Наверное, многие уже поняли данную закономерность:

Требуется найти минимальную/максимальную площадь? Составляем функцию площади;
Минимальную/максимальную диагональ? Составляем функцию длины диагонали;
Минимальный/максимальный периметр? Составляем функцию периметра
и т.д.

Напоминаю, что периметр – это длина границы фигуры, в данном случае – сумма длин сторон прямоугольника. Кстати, задачу легко переформулировать «чисто математически»:

«Найти прямоугольник максимальной площади, если его периметр равен 30 см»

Выполните схематический чертёж, подумайте, что обозначить за «икс» (впрочем, чего тут думать), составьте функцию площади 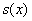– и дальше по накатанной.

Краткое решение и ответ в конце урока.

После простых разогревающих заданий рассмотрим что-нибудь поосновательнее:

На странице книги печатный текст должен занимать (вместе с промежутками между строк) 192 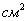. Верхнее и нижнее поля занимают по 4 см, левое и правое – по 3 см. Если принимать во внимание только экономию бумаги, то каковы должны быть наиболее выгодные размеры страницы?

Решение: разруливаем задачу по той же логической схеме:

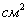
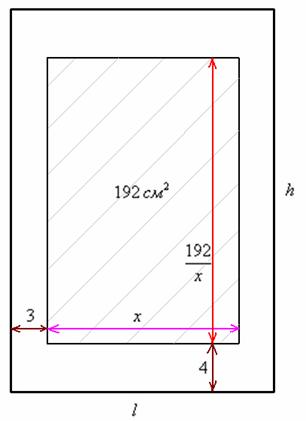
Что требуется найти? Наиболее выгодные размеры страницы. А страница обычно имеет форму прямоугольника. Коль скоро речь идёт об экономии бумаги, то, очевидно, нужно найти такую ширину и высоту листа, чтобы его площадь была минимальна. Из чего следует, что нам необходимо составить функцию площади страницы. Причём условие жёстко задаёт размеры полей, а вот под область печати отведено 192 и её размеры могут быть произвольными (заштрихованный прямоугольник на схематическом чертеже):

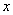
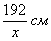
Обозначим за ширину области печати (малиновый отрезок) (можно обозначить высоту – получится равноценное решение). Тогда высота области печати:
(красный отрезок).

Учитывая известные значения полей, найдём ширину всего листа:

И его высоту:

Составим функцию площади листа и сразу подготовим её для дифференцирования:

Найдём критические точки:

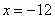
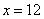
Точка не удовлетворяет геометрическому смыслу задачи, а вот значение куда более интересно.

Проверим выполнение достаточного условия экстремума: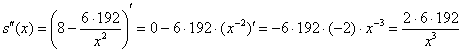

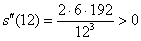
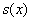
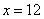
(считать тут совсем не обязательно), значит, функция достигает минимума в точке .

Таким образом, размеры оптимального листа: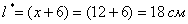
;
;
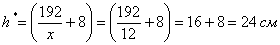
при этом минимальная площадь:

Ответ: ширина оптимальной страницы: 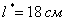, её высота: ; при этом минимальная площадь:

Как видите, основная трудность состоит в том, чтобы разобраться в условии и составить нужную функцию. И в преодолении этой трудности здОрово помогает чертёж. Поэтому всегда стараемся выполнить схематический чертёж или хотя бы рисунок. Даже в таких простых случаях, как в Задаче №3, не говоря уже о только что разобранном примере.

Следующее задание для самостоятельного решения:

В полукруг радиуса 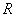вписать прямоугольник наибольшего периметра

Просто и со вкусом. И снова несколько подсказок, которые полезно иметь в виду и при решении других задач:

! Во-первых, обратите внимание, что условие сформулировано в общем виде и величина 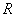считается известной. Если совсем тяжко, решите задачу с каким-нибудь конкретным значением радиуса, например, с радиусом .

! Во-вторых, выполните схематический чертёж, который здесь очень прост: одна из сторон прямоугольника лежит на диаметре полукруга, а вершины противоположной стороны – на полуокружности. Очевидно, что в полукруг можно вписать бесконечно много прямоугольников и ваша задача найти такой, периметр которого максимален. Какую функцию нужно составлять, надеюсь, всем понятно. Подумайте, что удобнее обозначить за «икс» и, кроме того, освежите в памяти теорему Пифагора.

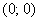
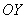
! В-третьих, задачу можно решить в разных стилях. Образец решения оформлен «исключительно геометрически», однако есть и такой вариант: начертить полукруг в декартовой системе координат – в верхней полуплоскости центром в точке . Далее составить уравнение окружности, выразить функцию верхней полуокружности и рассмотреть переменные координаты вершины прямоугольника, которая на этой полуокружности лежит. Более того, ввиду симметрии фигур относительно оси задачу можно решить в 1-й координатной четверти, т.е. изобразить лишь четвертинку круга (но затем не забыть удвоить одну из сторон прямоугольника). Кому как удобнее.

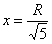
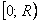
! И, в-четвёртых, эта задача о том, что иногда совсем не обязательно «разбивать лоб» о новый материал 😉 Если вам показался слишком сложным 2-й достаточный признак экстремума, то никто ведь не запрещает использовать 1-й достаточный признак – определите знаки первой производной слева и справа от критической точки на промежутке и сделайте вывод.

Наш урок в самом разгаре и настало время разобрать задачи, которые встречались в моей практике без преувеличения десятки раз:

Определите размеры открытого бассейна объемом 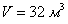, имеющего форму прямоугольного параллелепипеда с квадратным дном, на облицовку стен и дна которого уйдет наименьшее количество материала.

Решение: представили бассейн. Квадратное дно. Стены. Размеры бассейна однозначно определяются его длиной и шириной, которые в данном случае совпадают (по условию дно квадратное) и глубиной (высотой стенки). Требуется найти такие размеры бассейна, чтобы на облицовку его поверхности ушло наименьшее количество материала (например, плитки). Из чего следует, что нам нужно составить функцию суммарной площади дна и 4 стен. Изобразим на чертеже развёртку бассейна – его дно и 4 стенки, которые аккуратно лежат рядышком: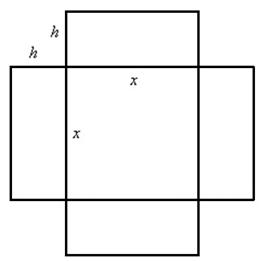

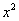
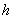
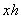
За «икс» здесь, конечно же, напрашивается обозначить сторону квадрата. Тогда площадь дна равна . Осталось выразить – высоту стены и найти её площадь .

По условию, объём бассейна равняется 32 кубическим метрам. Даже не вспоминая и не разыскивая соответствующую формулу, нетрудно сообразить, что объём прямоугольного параллелепипеда – это произведение площади его «дна» на высоту:

В нашем случае: .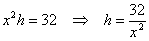

Составим функцию суммарной площади дна и четырёх одинаковых стен бассейна:

Найдем критические точки: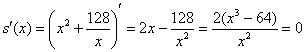

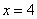
– критическая точка.

Проверим выполнение достаточного условия экстремума: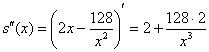

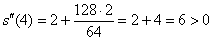
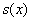
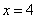
, значит, функция достигает минимума в точке .

Таким образом:
сторона оптимального бассейна ;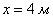
глубина ;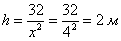
при этом минимальная площадь облицовки: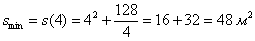
.

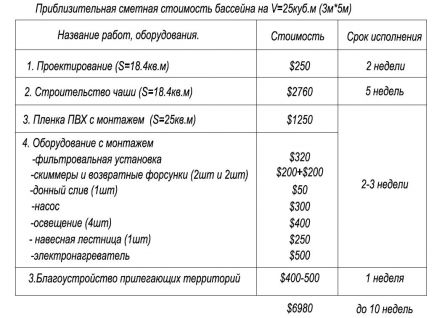
Ответ: сторона оптимального бассейна: 4 м, глубина: 2 м; при этом минимальная площадь облицовки .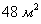

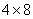
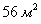
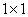
Кстати, это решение совсем не очевидно – так, например, на оптимальный вариант с успехом претендует «лягушатник» размером глубиной 1 метр, и «на глазок» очень трудно определить, что выгоднее – ведь площадь облицовки последнего лишь ненамного больше: . И да – надо отдать должное авторам задач за реалистичность, а то не так уж и редко получаются забавные результаты а-ля бассейн глубиной 32 метра, что называется, купайтесь и не квакайте =)

Аналогичная задача про суровые челябинские шпроты:

Каковы должны быть размеры консервной банки цилиндрической формы, чтобы на её изготовление пошло наименьшее количество материала, если объем банки 0,5 литра?

Но перед тем как решать, пожалуйста, ознакомьтесь с парой полезных замечаний:

Во-первых, литр – это единица объёма. Я специально заострил внимание на физике, поскольку на обывательском уровне литр очень часто неверно отождествляют с килограммом (единицей массы). Ощутите разницу – пол-литровая банка кильки и та же банка, наполненная гвоздями. Один литр равен одному кубическому дециметру или тысяче кубических сантиметров:

А теперь очень важный момент: так как размеры банки, очевидно, выразятся в сантиметрах, то 0,5 литра следует сразу перевести в кубические сантиметры!

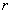
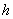
К слову, что это за размеры? Цилиндр стандартно определяется радиусом основания и высотой . Во-вторых. Освежим в памяти формулы:

площадь круга: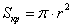
площадь боковой поверхности цилиндра: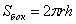
объём цилиндра:

И в который раз остановлюсь на важном принципе эффективного изучения математики: не зубрите формулы (без крайней необходимости, конечно). В частности, позабытую площадь боковой поверхности цилиндра несложно вывести даже в уме: представьте стенку консервной банки без дна и крышки. Сделайте вертикальный разрез и расправьте боковину на столе. В результате получился прямоугольник, одна из сторон которого, понятно, равна высоте банки 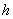, а другая – длине окружности . Площадь же прямоугольника рассчитывается элементарно:

Решение проводится по аналогии с Задачей 6, примерный образец в конце урока.

Закрепим типовик своего рода обратными задачами:

Определить наибольшую вместимость цилиндрического бака, если его площадь поверхности (без крышки) должна равняться

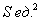
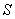
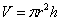
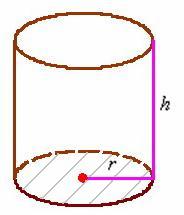
Решение: в данном случае всё наоборот – известна площадь поверхности (если трудно, замените конкретным числом) и требуется определить максимальный объём бака.

За «икс» обозначим… а зачем, собственно, лишние буквы? Ещё с первых уроков о производной многие поняли, что дифференцировать можно по любой переменной, и сейчас мы окончательно избавимся ото всех комплексов.

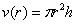
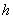
От какой переменной искать функцию объёма? В соответствующей формуле наиболее «наворочен» радиус, поэтому логично попытаться составить функцию , зависящую именно от него. Нужно только выразить высоту .

Сумма площадей дна (не забываем, что крышка отсутствует!) и боковой поверхности в точности равна известному значению: 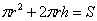, откуда находим:

Таким образом:

Найдём критические точки:

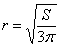
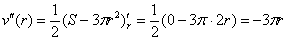
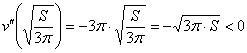
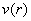
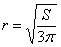
Геометрическому смыслу задачи, разумеется, удовлетворяет положительный корень . Проверим выполнение достаточного условия экстремума:

, значит, функция достигает максимума в точке .

При этом высота бака: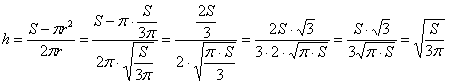

максимальный объём:

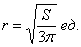
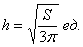
Ответ: радиус основания оптимального бака: , высота: , при этом максимальный объём:

Решение в общем виде, бывает, кажется непривычным, однако оцените его универсальность – теперь достаточно лишь подставить конкретное значение площади и сразу рассчитать размеры оптимального цилиндра.

Успокоительное задание для самостоятельного решения:

Прямоугольный лист картона имеет размеры 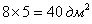. Требуется вырезать по его углам такие квадраты, чтобы после загибания оставшихся кромок получилась коробка наибольшей вместимости.

Краткое решение и ответ в конце урока.

Помимо рассмотренных выше геометрических объектов, на практике также можно встретить треугольники, трапеции, шары, конусы и т.д., но это более редкие гости (что касаемо забытых формул – справочники в помощь). К сожалению, нельзя объять необяътное, и поэтому в рамках этой статьи я ограничился самыми распространёнными примерами. И действительно, задач ведь придумать можно очень много – и всех их не перерешаешь, главное, чтобы вы хорошо поняли принципы и методы решения, которые я постарался изложить максимально пОлно и качественно.

Кроме того, существуют экстремальные задачи физического, химического, экономического и др. содержания, однако по причине отсутствия таковых в моей коллекции кот даже и не плакал. Но, понимая, что такое производная и обладая элементарной техникой дифференцирования, вы не должны испытать серьёзных затруднений с этими задачами, хотя для их решения, конечно, нужно разобраться и в самой физике/химии/экономике или иной предметной области.

Решения и ответы:

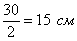
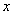
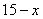
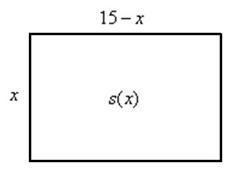
Пример 3: Решение: найдем полупериметр прямоугольника: . Обозначим через длину стороны прямоугольника (любую). Тогда – длина смежной стороны:

Составим функцию площади прямоугольника: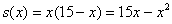
.
Найдем критические точки: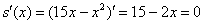

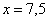
– критическая точка.
Проверим выполнение достаточного условия экстремума.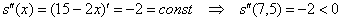
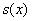
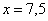
, значит, функция достигает максимума в точке .
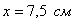
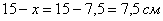
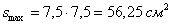
Таким образом – оптимальная длина стороны прямоугольника, длина смежной стороны: ; при этом максимальная площадь:

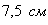
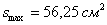
Ответ: оптимальный прямоугольник представляет собой квадрат со стороной ; при этом максимальная площадь: .

Пример 5: Решение: выполним чертёж: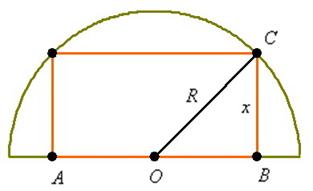

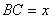
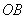
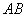
Пусть (как вариант, за «икс» можно обозначить или даже ).
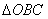
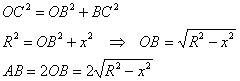
Рассмотрим прямоугольный . По теореме Пифагора:

Составим функцию периметра прямоугольника: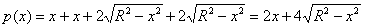

Найдём критические точки: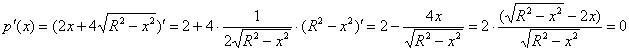
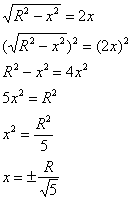
Решим простейшее иррациональное уравнение:

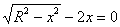
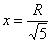
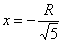
Уравнению удовлетворяет корень (корень же появился в результате возведения обеих частей в квадрат и является посторонним).
Проверим выполнение достаточного условия экстремума.
Способ первый: определим знаки производной: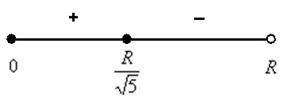

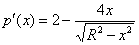
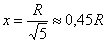
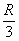
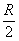
Примечание: используем стандартный метод интервалов: в производную подставляем какое-нибудь значение, лежащее левее точки , например, и подставляем какое-нибудь значение из правого интервала – проще всего взять .
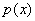
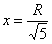
Вывод: функция достигает максимума в точке .
Способ второй: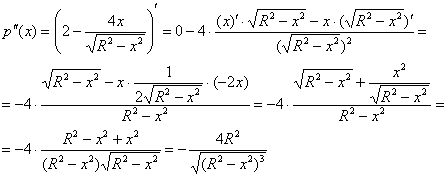

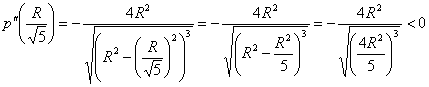
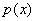
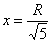
, значит, функция достигает максимума в точке .
Таким образом, размеры оптимального прямоугольника: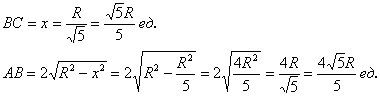

При этом максимальный периметр: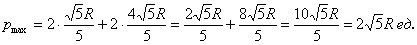

Ответ: оптимальный прямоугольник имеет размеры 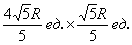, при этом максимальный периметр:

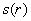
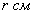
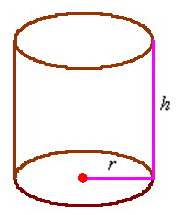
Пример 7: Решение: составим функцию площади полной поверхности цилиндра , зависящую от его радиуса. Пусть – радиус дна (и крышки) консервной банки:

Тогда площадь дна: 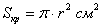. Столько же и площадь крышки.
По условию объём консервной банки равен :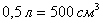

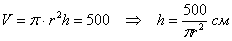
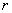
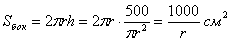
Выразим через площадь боковой поверхности банки:

Площадь полной поверхности банки равна сумме площадей дна, крышки и боковой поверхности: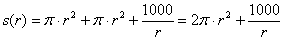

Найдём критические точки: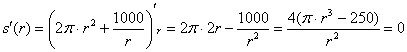

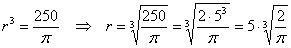
– критическая точка.
Проверим выполнение достаточного условия экстремума: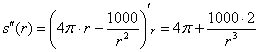

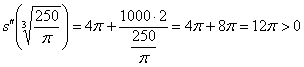
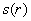
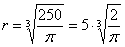
, значит, функция достигает минимума в точке .
Высота оптимальной банки: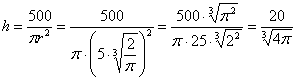

Ответ: радиус основания оптимальной банки: 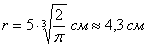, её высота:

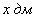
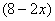
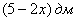
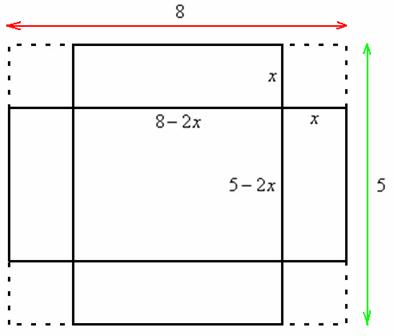
Пример 9: Решение: пусть – сторона вырезаемых по углам квадратов (высота будущей коробки). Тогда смежные стороны дна коробки составят и :

Составим функцию объёма коробки: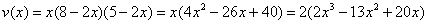

Найдём критические точки: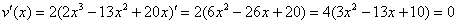

Решим квадратное уравнение: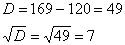

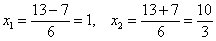
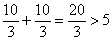
– критические точки. Второе значение не удовлетворяет геометрическому смыслу задачи, поскольку суммарная длина отреза сверху и снизу (ширины листа).
Проверим выполнение достаточного условия экстремума: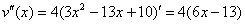

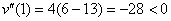
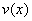
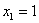
, значит, функция достигает максимума в точке .
Ответ: размеры оптимальной коробки:
– высота (сторона вырезаемых по углам квадратов);
– длина;
– ширина;
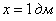
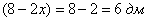
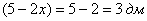
при этом максимальный объем: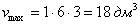
.

Автор: Емелин Александр

(Переход на главную страницу)

«Всё сдал!» — онлайн-сервис помощи студентам

Источник