Интеграл мора примеры решений

Расчетно-проектировочные работы и примеры их выполнения. Методическое пособие для студентов дневных / Основные задачи 2-го семестра

Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования «Тульский государственный университет» СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ Расчетно-проектировочные работы и примеры их выполнения Методическое пособие для студентов дневных и вечерних факультетов Часть 2

ОГЛАВЛЕНИЕ Раздел 1. ЭНЕРГЕТИЧЕСКИЙ МЕТОД ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ. ИНТЕГРАЛ МОРА И ПРАВИЛО ВЕРЕЩАГИНА……………………………………………….…….….5 1.1. Основные теоретические сведения и расчетные формулы ………. 5 1.2. Примеры решения типовых задач …………………………….….8 Раздел 2. РАСЧЁТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ КОНСТРУКЦИЙ МЕТОДОМ СИЛ……………………………………………………. 15 2.1. Основные понятия …………………………………………………….…15 2.2. Использование свойств симметрии при раскрытии статической неопределимости …………………………………………………………20 2.3. Определение перемещений в статически неопределимых системах….23 2.4 Расчёт многопролётных неразрезных балок с помощью уравнения трёх моментов………………………………………………………………..…24 2.5 Контроль правильности решения статически неопределимой системы…………………………………………………………………. 27 Раздел 3. КОСОЙ ИЗГИБ ………………………………………………………. 66 3.1. Определение понятия «косой изгиб».…………………………………66 3.2. Брус прямоугольного поперечного сечения ………………………….…67 3.3. Положения опасных сечений ……………………………………….……68 3.4. Нулевая линия и опасные точки………………………………………….71 3.5. Брус круглого сечения…………………………………………………….72 Раздел 4. РАСЧЕТ БРУСА БОЛЬШОЙ ЖЕСТКОСТИ НА ПРОЧНОСТЬ ПРИ ВНЕЦЕНТРЕННОМ РАСТЯЖЕНИИ-СЖАТИИ………………..…94 4 . 1 Определение напряжений и положения нулевой линии…………. …94 4.2. Ядро сечения…………………………………………………………..100

4.3. Контрольные вопросы……………………………………………….106 Раздел 5. ИССЛЕДОВАНИЕ НАПРЯЖЕННОГО И ДЕФОРМИРОВАННОГО СОСТОЯНИЯ В ТОЧКЕ УПРУГОГО ТЕЛА……………………..127 5.1. Основные понятия о напряженном состоянии в точке. Тензор напряжений………………………………………………………. …..127 5.2. Объемное напряженное состояние……………………………………..129 5.3. Плоское напряженное состояние…………………………………….…143 5.4. Теория деформаций………………………………………………….….150 Раздел 6. РАСЧЕТ ПРОСТРАНСТВЕННОГО БРУСА НА ПРОЧНОСТЬ…178 6.1 6.2 Методические указания………………………………………….….178 6.3 Пример выполнения работы……………………………………..…181 Раздел 7. РАСЧЕТ ВАЛА КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ НА СО ВМЕСТНОЕ ДЕЙСТВИЕ ИЗГИБАЮЩИХ И КРУТЯЩИХ МОМЕНТОВ…………………………………………………………191 7.1 Основные теоретические сведения и расчетные формулы………….191 Раздел 8. РАСЧЕТ СЖАТЫХ СТЕРЖНЕЙ НА УСТОЙЧИВОСТЬ…………206 8.1. Понятие об устойчивости равновесия упругих тел………………206 8.2. Продольный изгиб………………………………………………. …208 8.3. Потеря устойчивости при напряжениях, превышающих предел пропорциональности…………………………………………….….212 8.4. Практические расчеты на устойчивость……………………..……214 8.5. Контрольные вопросы…………………………………………….223

Раздел 9. РАСЧЕТ ЦИЛИНДРИЧЕСКИХ ПРУЖИН С МАЛЫМ ШАГОМ ВИТКА…………………………………………………………..…225 9.1. Основные теоретические сведения……………………………….225

РАЗДЕЛ 1. Энергетический метод определения перемещений. Интеграл Мора и правило Верещагина Основные теоретические сведения и расчетные формулы Энергетический метод определения перемещений в стержневых системах, предложенный немецким ученым Отто Мором, является наиболее общим методом определения линейных и угловых перемещений в стержневых системах. Формула Мора для определения обобщенного перемещения (линейного или углового) произвольного сечения стержневой системы имеет следующий вид

M	x	M	1x dz	M y M 1y	dz	M кр M 1кр	dz	N	z	N	1 dz , (1.1)
l	E I x		l	E I y	l	G I	l	E F

где — искомое перемещение (линейное или угловое) по заданному направлению под действием внешних нагрузок; M x , M y , M кр , N z — внутренние силовые факторы в произвольно вы- бранном поперечном сечении рассматриваемого стержня от заданной (внешне й) наг ру зки; M 1x , M 1y , M 1кр , N 1z — то же от единичной обобщенной силы (сосредоточенной силы или сосредоточенного момента), приложенной в точке, перемещение которой определяется. Если определяется линейное перемещение в некотором направлении, то в этом направлении прикладывается единичная сила P 1 ; при определении углового перемещения сечения прикладывается единичный момент M 1 любого направления; E I x , E I y , E A, G I — жесткости стержня соответственно при изгибе в вертикальной и горизонтальной плоскостях, растяжении (сжатии), кручении. Формула (1.1) не учитывает влияния поперечных сил, так как перемещения, вызванные ими, большей частью малы по сравнению с перемещениями, соответствующими продольным усилиям, изгибающим и крутящим моментам. Интегрирование по формуле (1.1) производится по длине каждого участка, а суммирование распространяется на все участки стержня. Формула Мора для отдельных частных случаев имеет более простой вид. 1. Для балок и плоских рам, состоящих из прямолинейных стержней

M x M 1x dz	(1.2)
l E I x

2. Для ферм, стержни которых работают на растяжение – сжатие

N z N 1z	dz	(1.3)
E A
l

Если рассматриваются шарнирные фермы, составленные из прямых стержней постоянного поперечного сечения, формула (1.3) принимает вид

N z N 1z		l	(1.3а)
E A
3. Для пространственных стержневых систем
M	x	M	1x dz	M y M	1y	dz	M кр M	1кр	dz .	(1.4)
l		E I x		l	E I y		l	G I

Для определения перемещений при плоском поперечном изгибе по формуле Мора необходимо выполнить следующие операции: 1. рассмотреть так называемое грузовое ( заданное ) состояние конструкции и записать аналитические выражения для внутренних усилий, возникающих в выбранном поперечном сечении стержня при действии внешних нагрузок; 2. рассмотреть единичное состояние — снять с конструкции все действующие на нее нагрузки и приложить в сечении, перемещение которого определяется, по заданному направлению единичную силу (при определении линейного перемещения) или единичный момент (при вычислении углового перемещения); 3. записать выражения для изгибающих моментов M 1 , действующих в произвольно выбранном поперечном сечении каждого стержня от единичной нагрузки; 4. составить интеграл Мора и после интегрирования по участкам всей конструкции вычислить искомое перемещение. Если оно получилось отрицательным, то это означает, что действительное перемещение противоположно принятому направлению единичной нагрузки. Примечание . Если требуется определить взаимное перемещение двух точек по какому-либо направлению, следует снять с конструкции внешние нагрузки и затем приложить в рассматриваемых точках по единичной
силе (моменту), действующих по линии (направлению) искомого перемещения и направленных противоположно. Рассмотрим способ вычисления интеграла Мора, предложенный в 1925 году студентом Московского института инженеров железнодорожного транспорта Верещагиным А.К. – способ перемножения эпюр (правило Верещагина) . Этот способ применим для определения перемещений в конструкциях, состоящих из прямолинейных элементов, жесткость которых в пределах отдельных участков постоянна. Для определения перемещений по Верещагину необходимо: 1. построить эпюры внутренних силовых факторов от действия внешних сил, например, при изгибе — эпюру изгибающих моментов; 2. построить эпюры внутренних силовых факторов от действия единичной силы (момента), приложенной в сечении, перемещение которого определяется, по заданному направлению; например, при изгибе — единичную эпюру изгибающих моментов; 3. вычислить искомое перемещение для каждого участка путем умножения площади нелинейной эпюры на ординату линейной эпюры, взятую под центром тяжести нелинейной и деления результата на жесткость рассматриваемого участка . В тех случаях, когда обе эпюры прямолинейны, можно умножать площадь любой из них на ординату другой под центром тяжести первой. Формула Верещагина для изгиба имеет вид

y c
E I x	(1.5)
где — площадь нелинейной эпюры;	y c — ордината линейной эпюры,
расположенная под центром тяжести	нелинейной; E I х — жесткость

участка стержня при изгибе. Произведение y c отрицательно, если эпюры от внешних нагрузок и единичной силы (момента) противоположны по знаку, т.е. расположены по разные стороны от оси стержня. Это означает, что направление перемещения противоположно направлению единичной силы (момента). При вычислении перемещений от действия крутящих моментов или продольных усилий в знаменатель формулы (1.5) вводится вместо жесткости при изгибе E I x соответственно жесткость при кручении G I или при растяжении растяжении-сжатии E A . Если эпюра от внешней нагрузки имеет сложный вид, то рекомендуется ее представить в таком виде, чтобы вычисление ее площади и определение положения центра тяжести было наиболее простым. Способы, упрощающие вычисления перемещений по формуле Верещагина, будут рассмотрены ниже на конкретных примерах. На рис.1.1 для справки приведены формулы для определения площадей участков эпюр и положения их центров тяжести.

h

C

l/2

l/2

l h C l/3 l h 1

C 1
C 2	h 2
l/3	l/3
l

C l/2 l

C 1

C 2

l/3 l/2 l

h 1	C 1
l/3		C 2	h 2
	l/3

l

h 1	C 1
C 3
l/3	C 2	h 2
l/2

l

l/3

l h 2 1 l h 1 1 2 l h 12 1 2 l h 2 q l 3 12 1 1 2 l h 2 q l 3 12 1 1 2 l h 12 1 2 l h 2 1 1 2 l h 12 1 2 l h 2 3 q l 3 12

Примеры решения типовых задач раздела «Энергетический метод определения перемещений. Интеграл Мора и правило Верещагина» Определение перемещений с помощью интеграла Мора Пример 1.1 . С помощью интеграла Мора определить прогиб и угол поворота сечения на конце консоли (рис.1.2, а ). Жесткость балки постоянна и равна E I x .

y
P=ql	q
z
z
x	l
a

1 б 1 в Рис. 1.2 Решение . Рассматриваем балку в системе координат X , Y , Z , помещая ее начало в крайнее левое сечение. Для грузового (заданного) состояния записываем выражение изгибающего момента в произвольно выбранном сечении с абсциссой z :

M x q l z q z	z	q l z q	z 2	.
	2		2

Для определения прогиба прикладываем на конце консоли единичную силу (рис.1.2, б ) и вычисляем величину изгибающего момента от этой силы: M 1x 1 z .
Вычисляем искомый прогиб, записывая интеграл Мора

qz 2	qz 4 l
M x M 1x		dz	l ( qlz	2 ) ( 1 z )	qlz 3	11ql 4
A	E I x		E I x	dz	24E I x
		3E I x		8E I x
l	0	0

. Величина прогиба получена со знаком «+», т.е. он направлен в ту же сторону, что и единичная сила (вниз). Для определения угла поворота прикладываем на конце консоли единичный момент (рис.1.2, в ) и вычисляем величину изгибающего момента в сечении с абсциссой z : M 1x 1 . Вычисляем искомый угла поворота сечения, записывая соответствующий интеграл Мора

M x M 1x	l ( qlz		qz	2	) 1	qlz 2	qz 3	l	3
			dz	2						2ql
E I x	E I x			dz	2E I x	3E	.
			6 E I x				I x
l	0	0

Знак минус означает, что направление угла поворота сечения противоположно выбранному направлению единичного момента (против хода часовой стрелки). Пример 1.2. Методом Мора определить прогиб балки в сечении A , если E 2 10 11 Па, I x 1500 10 8 м 4 (рис.1.3, а ).

Источник

Метод Мора. Интеграл Мора

Теорема Кастельяно дала нам возможность определять перемещения. Эту теорему используют для отыскания перемещений в пластинках, оболочках. Однако, вычисление потенциальной энергии громоздкая процедура и мы сейчас наметим более простой и наиболее общий путь определения перемещений в стержневых системах.

Пусть задана произвольная стержневая система и нам нужно определить в ней перемещение точки по направлению , вызванное всеми силами системы —

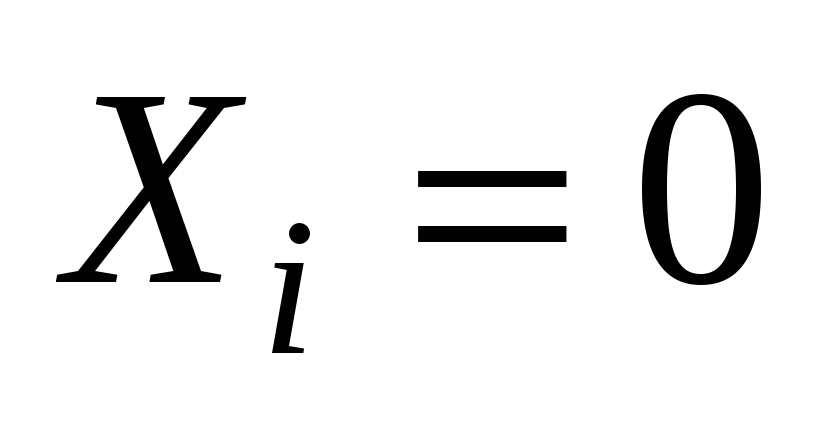
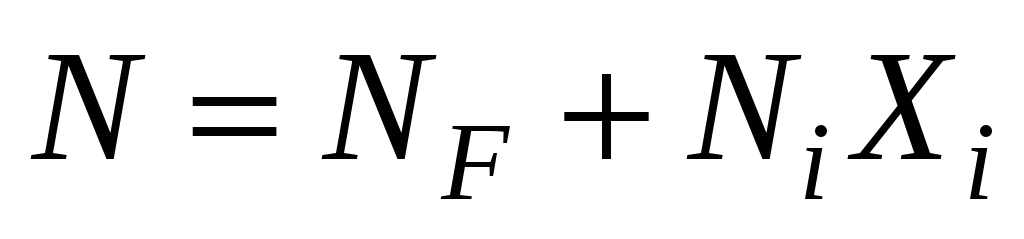
Т.к. в общем случае в системе нет силы, приложенной по направлению искомого перемещения, то воспользоваться теоремой Кастельяно нельзя. Добавим к числу прочих сил силу , приложенную к точке и действующую в направлении . Тогда внутренние силовые факторы в системе можно выразить

, где — внутренние силовые факторы в системе от действующих сил;

— внутренние силовые факторы от силы .

Внесем эти выражения в (3)

По теореме Кастельяно:

Учтя, что

получаем выражение:

называемое интегралом Мора.

Для того, чтобы определить перемещение с помощью метода Мора, необходимо:

1) Определить внутренние силовые факторы в системе от заданных сил.

2) Приложить по направлению искомого перемещения единичную обобщенную силу (единичную силу для определения линейного перемещение, пару сил с моментом равным единице для определения углового перемещения и определить внутренние силовые факторы от единичной силы.

3) Подставить полученные ранее выражения в интеграл Мора и определить перемещение.

Для систем, работающих на изгиб: балок, рам, влияние нормальных сил на величину перемещения незначительно и интеграл Мора в этом случае выглядит:

Источник