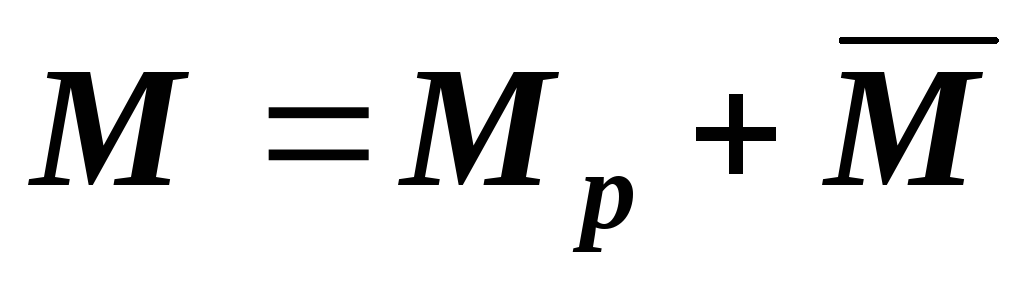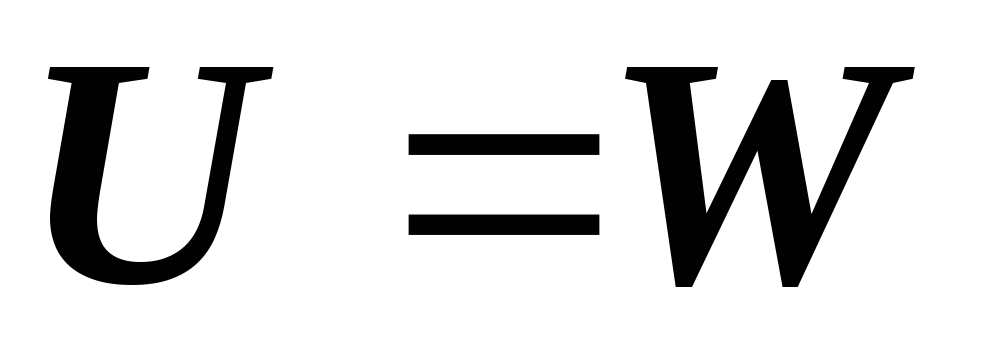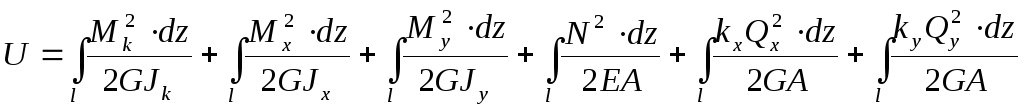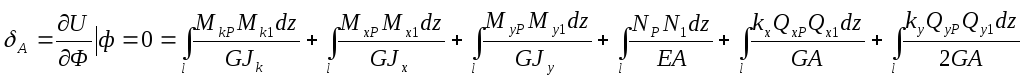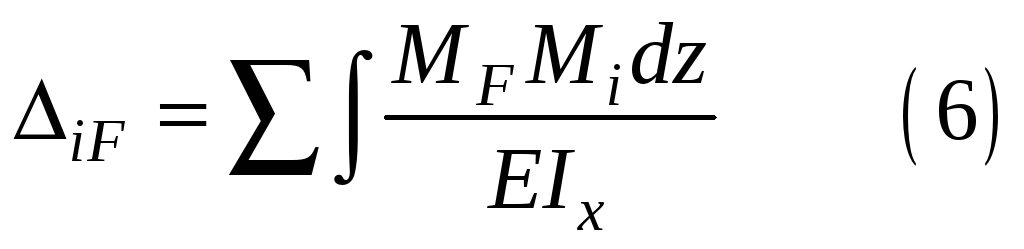Интеграл мора при растяжении сжатии

4. Интеграл Мора для вычисления перемещений

Вывод формулы проводится для случая плоского изгиба, соответственно учитывается только изгибающий момент . В общем случае нагружения рассуждения аналогичны.

Задана произвольная упругая система, загруженная силами . Требуется определить перемещение произвольной точки в заданном направле-

нии .

Для вывода формулы кроме заданной рассмотрим вспомогательную единичную систему, которая представляет собой заданную упругую систему (рис. 105), к которой по направлению искомого перемещения приложена единичная сила .

Введем обозначения:

изгибающий момент —

работа внешних сил —

—

изгибающий момент —

работа силы —

—

По первому свойству упругих систем справедливы равенства:

Загрузим систему последовательно сначала единичной силой , а затем, не снимая ее, заданными силами . Из равенства энергии и работы после двух нагружений можно найти перемещение.

Работа после первого нагружения ,

после второго нагружения ,

суммарная ,

Изгибающий момент после двух нагружений

Вычисляем

Приравниваем

;

По аналогии можно вывести формулу интеграла Мора для всех случаев нагружения.

5. Частные случаи записи интеграла Мора

При расчете разных упругих систем учитывают соответствующие силовые факторы, поэтому используют разные формы записи интегралов Мора.

1. Для шарнирных стержневых систем:

2. Для плоских балок, рам и кривых брусьев

3. Для пространственных систем

6. Порядок определения перемещений по интегралу Мора

Для определения перемещений надо рассмотреть заданную и единичную системы. При определении линейного перемещения по направлению искомого перемещения прикладывается единичная сила, а при определении угла поворота сечения – единичный момент.

ычерчиваем заданную и вспомогательную системы (рис. 106), разбиваем их на участки. Границы участков в обеих системах должны совпадать. Для двух систем по участкам записываем выражения силовых факторови составляем интегралы Мора, вычислив которые, получим величину искомого перемещения.

Участок :Участок:

;

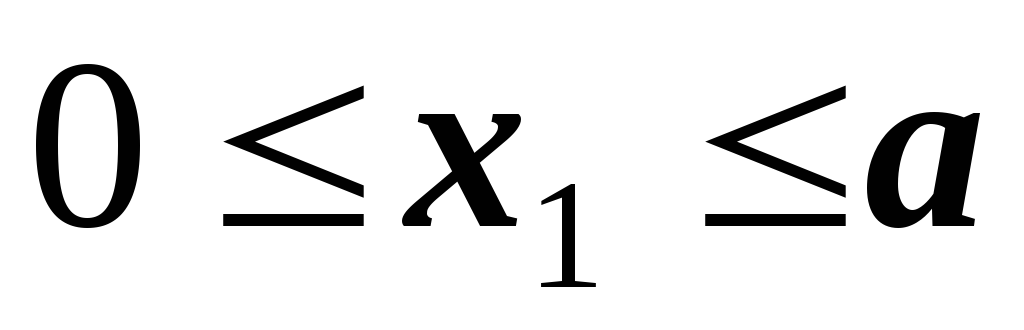
7. Правило Верещагина для вычисления интеграла Мора («перемножение» эпюр)

Интеграл Мора содержит силовые факторы от заданной нагрузки и единичных сил. Метод Верещагина основан на том, что эпюра от единичной силы и момента всегда прямолинейна, никогда не бывает параболы. Жесткость по участкам должна быть постоянной, чтобы ее можно было вынести за знак интеграла.

Вывод проводим на примере эпюр изгибающих моментов (рис. 107), но результат справедлив для любых эпюр, из которых одна линейная.

Постановка задачи: на участке балки с постоянной жесткостьюзаданы эпюрыи. Эпюраимеет произвольное очертание, эпюра— прямая линия без изломов.

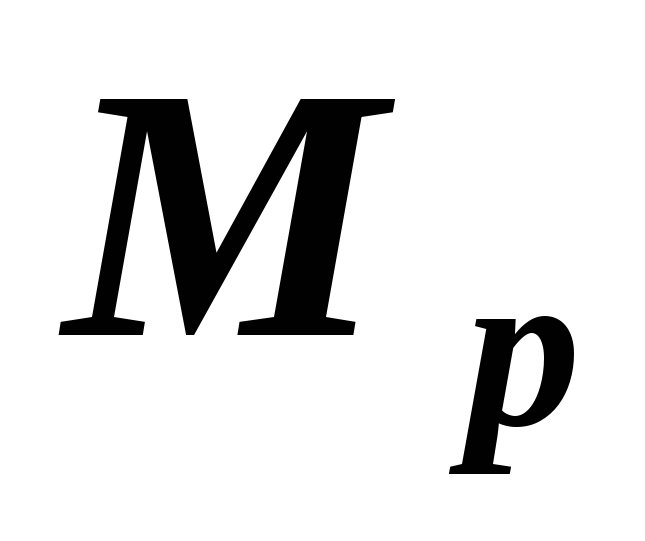
Требуется вычислить интеграл

Получено выражение, позволяющее вычислять интеграл Мора геометрически. Этот способ вычисления называется методом Верещагина.

Правило: Чтобы вычислить интеграл Мора по способу Верещагина нужно построить эпюры подинтегральных функций и, а затем площадь эпюры, обозначаемую, умножить на ординату с эпюрырасположенную под центром тяжести площади, обозначенную —.

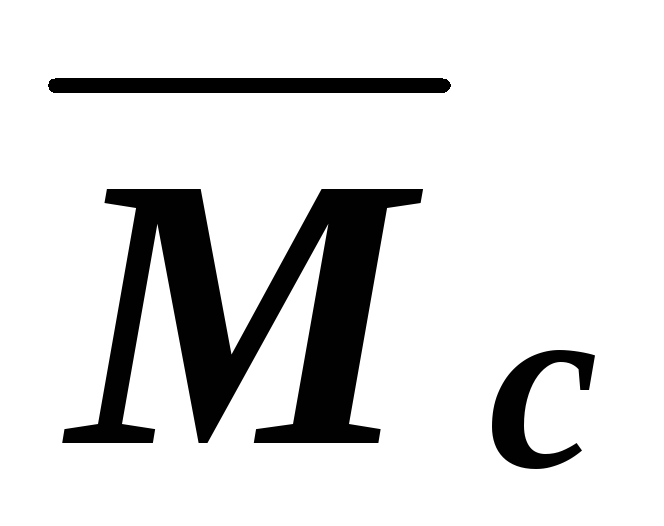
Примечание: Если обе «перемножаемые» эпюры прямолинейные, то, можно, наоборот, площадь брать с эпюры , а ординату с эпюры_.

.

Источник

2)Интеграл Мора для определения перемещений

Если необходимо найти перемещение точки, к ко­торой приложены внешние силы, мы сами прикладываем в этой точке внешнюю силу Ф в интересующем нас направлении. Далее, составляем выражение потенциальной энергии системы с учетом силы Ф. Дифференцируя его по Ф, находим переме­щение рассматриваемой точки по направлению приложенной силы Ф. Теперь остается вспомнить, что на самом деле силы Ф нет, и положить ее равной нулю. Таким образом, можно определить искомое перемещение.

П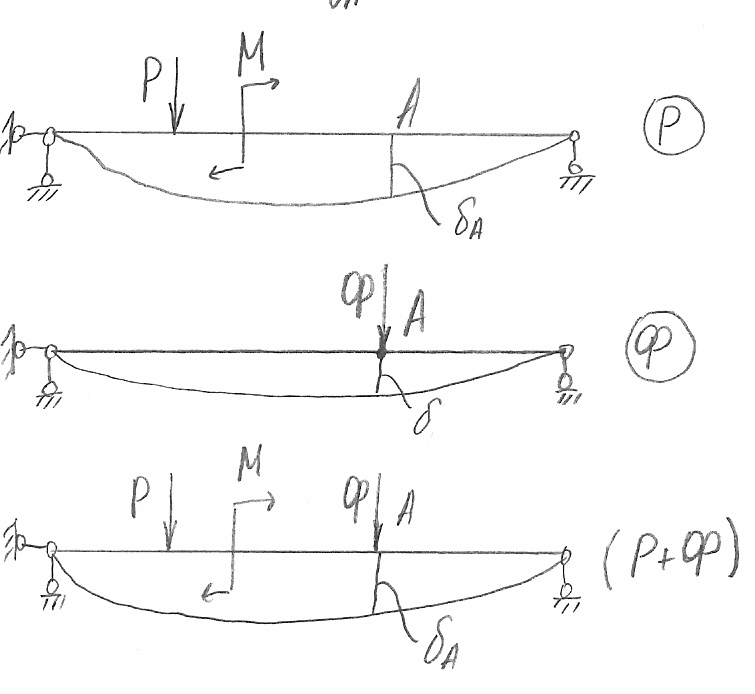риложим в точкеА по направлению Хl силу Ф. Внутрен­ние силовые факторы в каждом поперечном сечении при этом, вообще говоря, изменятся на величины, зависящие от силы Ф. Например, крутящий момент в некотором поперечном сечении будет иметь вид

где первое слагаемое представляет собой момент, который возникает под действием заданной системы внешних сил, а вто­рое слагаемое — дополнительный момент, который появляет­ся в результате приложения силы Ф. Понятно, что и М_КР, и М_КФ, являются функциями z, т.е. изменяются по длине стержня. Аналогично появляются дополнительные слагаемые и у остальных внутренних силовых факторов: М_Х = М_ХР + М_ХФ, М_У = М_УР + М_УФ и т.д.

Дополнительные силовые факторы Мкф, Мхф,… пропорциональны Ф.

Где M_К1, M_Х1 . — некоторые коэффициенты пропорциональ­ности, зависящие от положения рассматриваемого сечения, Т.е. переменные по длине стержня.

Если исключить систему внешних сил и заменить силу Ф единичной силой, то M_k = M_k1, M_x = M_x1 и т. д. Следо­вательно, Мк1, Мх1, Му1, N1, Qx1 и Qy1 — внутренние силовые факторы, возникающие в поперечном сечении под действием единичной силы, приложенной в рас­сматриваемой точке в заданном направлении.

Вернемся к выражению энергии

И заменим внутренние силовые факторы их значениями

Дифференцируя это выражение по Ф и полагая после этого Ф = О, находим перемещение точки А:

Полученные интегралы носят название интегралов Мора.

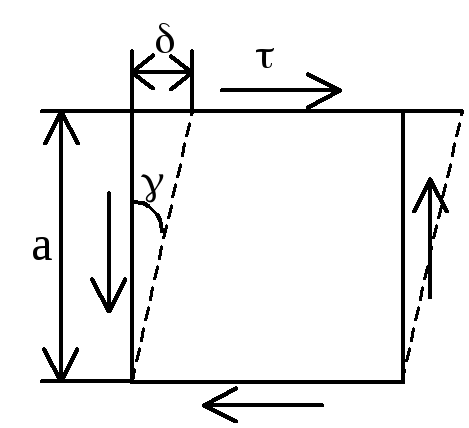
1)Напряженное состояние «чистый сдвиг»: определение, условие парности касательных напряжений, напряжение в наклонных площадках

Чистым сдвигом называют такой вид напряженного состояния, при котором по граням выделенного из материала элемента действуют только касательные напряжения.

Напряжение в наклонных сечениях (площадках)

Рассмотрим более подробно особенности напряженного состоя­ния, возникающего в однородном растянутом стержне. Определим напряжения, возникающие на некоторой наклонной площадке, со­ставляющей угол  с плоскостью нормального сечения (рис. 2.6, а).

Из условия z = 0, записанного для отсеченной части стержня (рис. 2.6, б), получим:

где F  площадь поперечного сечения стержня, F = F/cos   пло­щадь наклонного сечения. Из (2.17) легко установить:

Раскладывая напряжение р по нормали и касательной к на­клонной площадке (рис. 2.6, в), с учетом (2.18) получим:

 = p cos  =  cos2 ;  = p sin  =  sin 2  . (2.19)

Полученные выражения показывают, что для одной и той же точки тела величины напряжений, возникающих в сечениях, про­ходящих через эту точку, зависят от ориентации этой площадки, т.е. от угла. При  = 0 из (2.19) следует, что  = ,  = 0. При  = , т.е. на продольных площадках, =  = 0. Это означает, что продольные слои растянутого стержня не взаимодействуют друг с другом. Касательные напряжения  принимают наибольшие зна­чения при  = , и их величина составляетmax=. Важно отме­тить, как это следует из (2.19), что. Следовательно, в любой точке тела на двух взаимно перпендикулярных площадках касательные напряже­ния равны между собой по абсолютной величине. Это условие является общей закономерностью любого напряженного состояния и носит название

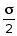
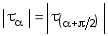
закона парности касательных напряжений

Чистый сдвиг — напряженное состояние, при котором по взаимно перпендикулярным площадкам (граням) элемента возникают только касательные напряжения. Касательные напряжения ,где Q — сила, действующая вдоль грани, F — площадь грани. Площадки, по которым действуют только касательные напряжения, называются площадками чистого сдвига. Касательные напряжения на них — наибольшие. Чистый сдвиг можно представить как одновременное сжатие и растяжение, происходящее по двум взаимно перпендикулярным направлениям. Т.е. это частный случай плоского напряженного состояния, при котором главные напряжения: ₁= — ₃ = ; ₂= 0. Главные площадки составляют с площадками чистого сдвига угол 45 о .

При деформации элемента, ограниченного площадками чистого сдвига, квадрат превращается в ромб. — абсолютный сдвиг,

  —относительный сдвиг или угол сдвига.

Источник

Метод Мора. Интеграл Мора

Теорема Кастельяно дала нам возможность определять перемещения. Эту теорему используют для отыскания перемещений в пластинках, оболочках. Однако, вычисление потенциальной энергии громоздкая процедура и мы сейчас наметим более простой и наиболее общий путь определения перемещений в стержневых системах.

Пусть задана произвольная стержневая система и нам нужно определить в ней перемещение точки по направлению , вызванное всеми силами системы —

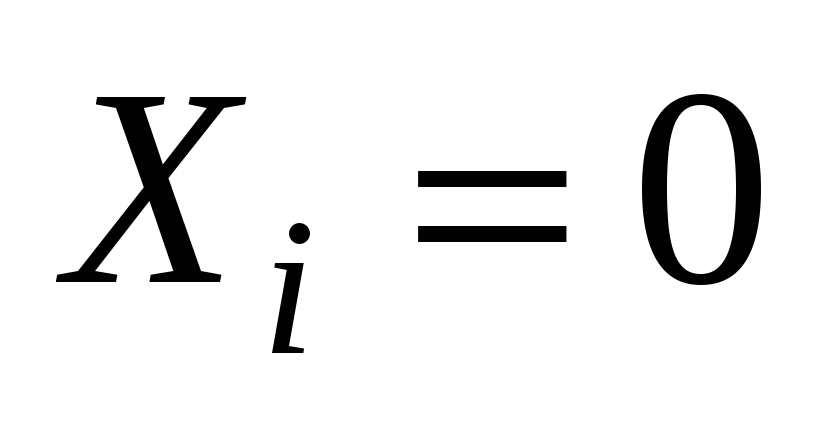
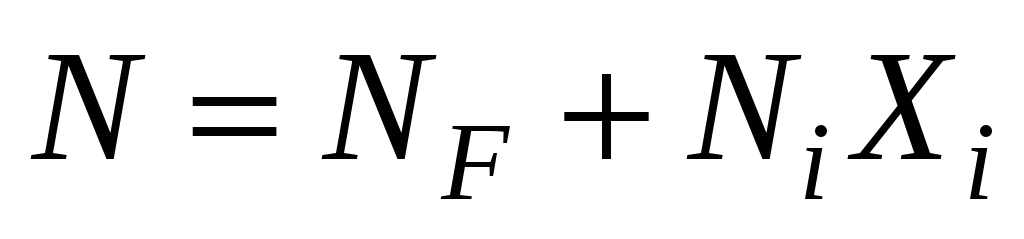
Т.к. в общем случае в системе нет силы, приложенной по направлению искомого перемещения, то воспользоваться теоремой Кастельяно нельзя. Добавим к числу прочих сил силу , приложенную к точке и действующую в направлении . Тогда внутренние силовые факторы в системе можно выразить

, где — внутренние силовые факторы в системе от действующих сил;

— внутренние силовые факторы от силы .

Внесем эти выражения в (3)

По теореме Кастельяно:

Учтя, что

получаем выражение:

называемое интегралом Мора.

Для того, чтобы определить перемещение с помощью метода Мора, необходимо:

1) Определить внутренние силовые факторы в системе от заданных сил.

2) Приложить по направлению искомого перемещения единичную обобщенную силу (единичную силу для определения линейного перемещение, пару сил с моментом равным единице для определения углового перемещения и определить внутренние силовые факторы от единичной силы.

3) Подставить полученные ранее выражения в интеграл Мора и определить перемещение.

Для систем, работающих на изгиб: балок, рам, влияние нормальных сил на величину перемещения незначительно и интеграл Мора в этом случае выглядит:

Источник