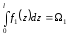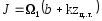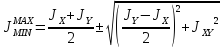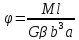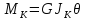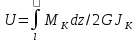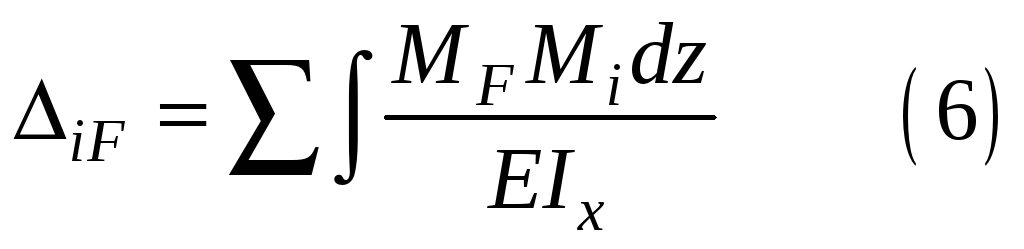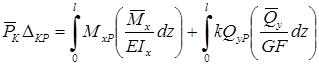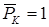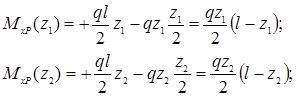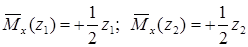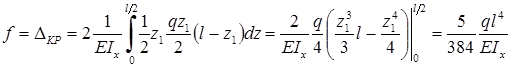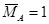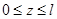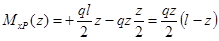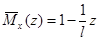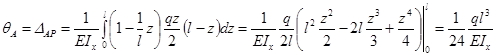Интеграл мора при изгибе использование правила верещагина

2)Вывод формулы способа Верещагина для вычисления интеграла Мора.

Если стержень состоит из прямых участков с постоянной в пределах каждого участка жесткостью, эпюры от единич­ных силовых факторов на прямолинейных участках оказыва­ются линейными.

Положим, на участке длиной 1 нужно взять интеграл от произведения двух функцийf₁(z)*f₂(z):J =f₁ (z) f₂(z) dz (1)

при условии, что хотя бы одна из этих функций — ли­нейная. Пусть f₂(Z) =b +kz. Тогда выражение (1) примет видJ =f₁ (z) dz+ kzf₁ (z) dz

Первый из написанных интегралов представляет собой пло­щадь, ограниченную кривой f₁ (z) (рис. 5.18), или, короче го­воря, площадь эпюрыf₁(z):

Второй интеграл характеризует статический момент этой пло­щади относительно оси ординат, т.е.

где Zц.т — координата центра тяжести первой эпюры. Теперь получаем

Но =f₂(z_ц.т.) Следовательно,

Таким образом, по способу Верещагина операция интегри­рования заменяется перемножением площади первой эпюры на ординату второй (линейной) эпюры под центром тяжести первой.

Билет 20

1)Главные осевые моменты инерции. Определение их величин и направлений главных осей.

Оси, относительно которых центробежный момент J_XcYc=0, наз-ся главными. Осевые моменты инерции относительно главных осей наз-ся главными моментами инерции.

«+» соответсвует максимальному моменту инерции, « — » — минимальному. После того как сечение вычерчено в масштабе и показано положение главных осей на глаз устанавливается направление осей (которой из двух соответствует максимальный, а которой – минимальный момент инерции).

2) Кручение стержня прямоугольного поперечного сечения (определение напряжений и перемещений).

На рисунке показана полученная методом теории упругости эпюра касательных напряжений для бруса прямоугольного сечения. В углах, как мы видим, напряжения равны нулю. Наибольшие напряжения возникают по серединам больших сторон, в точках А:

τ_А= τ_max=

_в=τ_max, где а — большая, b — малая сторона прямоугольника. Коэффициентыизависят от отношения сторонКоэффициент β также зависит от этого отношения. Эти данные приводятся в таблицах.

Угловое перемещение:

Ф-ла для расчёта касательных напряжений: , где

для расчёта углового перемещения:

Для прямоугольника: ,–геометрические параметры, зависящие от формы сечения.

Потенциальная энергия, накопленная закрученным брусом:

Билет 21

1)Определение перемещений при растяжении-сжатии.

, где W – перемещение, – удлинение, N – внутренняя сила на участке, E – модуль упругости первого рода, А – площадь поперечного сечения на участке.

Для однородного стержня длины , при Е= const, N = const:

2) Расчёт на прочность при изгибе. Понятие о расчётном и нормативном коэффициенте запаса.

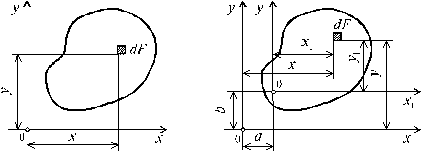
По принципу независимости действия сил нормаль­ное напряжение в произвольной точке, принадлежащей попереч­ному сечению бруса и имеющей координаты x, y, опр-ся суммой напр-й, обусловленных моментами M_x и M_y , т.е. (5.26)

Mx = Msin; My = Mcos, где- угол между плоскостью главного мемента М и осью Ох или Оу. (5.25)

Правило знаков для моментов: момент считается положительным, если в первой четверти координатной плоскости (там, где координаты x и y обе положительны) он вызывает сжимающие напряжения.

Если изгиб чистый, то один из моментов M_x или M_y равен 0 и выражение (5.26) принимает вид

, где — осевой момент сопротивления,– осевой момент инерции,— расстояние по модулю до наиболее удалённой точки сечения от Ох.

При косом изгибе М_Х , М_{У .}

Уравнение нейтральной линии, т.е. геометрического места точек, где нормальное напряжение принимает нулевые значения, находят, полагая в (5.26)  = 0:

Откуда определяется: (5.27)

Эпюра напряжений в поперечных сечениях бруса линейна, следовательно, максимальные напряжения в сечении возникают в точках наиболее удаленных от нейтральной линии.

Расчёт на прочность при изгибе проводится при условиях:

материал работает одинаково на растяжение и сжатие, т.е.

Условие прочности: , где,, где– допускаемое значение предела текучести,— коэф. запаса.

если неодинаково, то работают два условия:

, где,

Если расчёт проектировочный, то из двух коэффициентов выбирется наибольший. В поверочном – наоборот.

В целях безопасной работы напряжения должны быть ниже предельных значений для данного материала. Таким образом при поверочном расчёте (нахожд. Нормативного коэф. запаса):

, где — предельное кас. напряжение материала,n_Т – коэф. запаса,

за расчётный коэффициент принимают [n] > n_Т, где [n] – нормативный (предписываемый нормами проектирования конструкций) коэф. запаса.

Источник

Метод Мора. Интеграл Мора

Теорема Кастельяно дала нам возможность определять перемещения. Эту теорему используют для отыскания перемещений в пластинках, оболочках. Однако, вычисление потенциальной энергии громоздкая процедура и мы сейчас наметим более простой и наиболее общий путь определения перемещений в стержневых системах.

Пусть задана произвольная стержневая система и нам нужно определить в ней перемещение точки по направлению , вызванное всеми силами системы —

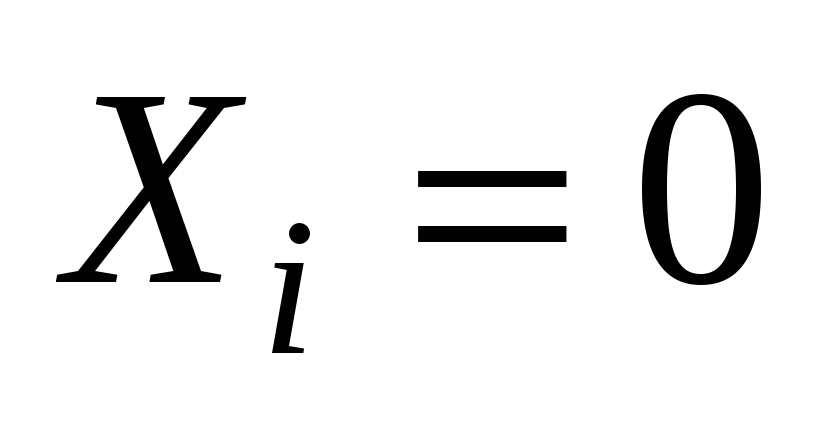
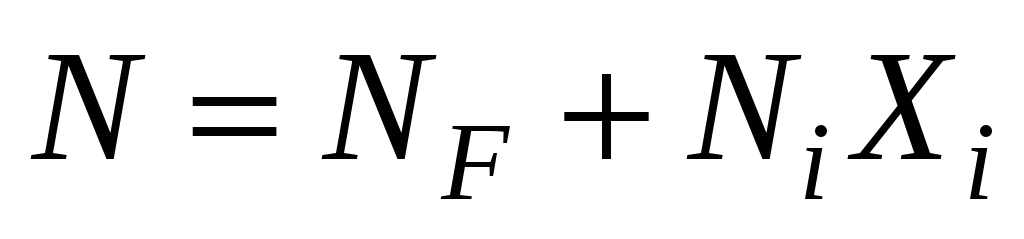
Т.к. в общем случае в системе нет силы, приложенной по направлению искомого перемещения, то воспользоваться теоремой Кастельяно нельзя. Добавим к числу прочих сил силу , приложенную к точке и действующую в направлении . Тогда внутренние силовые факторы в системе можно выразить

, где — внутренние силовые факторы в системе от действующих сил;

— внутренние силовые факторы от силы .

Внесем эти выражения в (3)

По теореме Кастельяно:

Учтя, что

получаем выражение:

называемое интегралом Мора.

Для того, чтобы определить перемещение с помощью метода Мора, необходимо:

1) Определить внутренние силовые факторы в системе от заданных сил.

2) Приложить по направлению искомого перемещения единичную обобщенную силу (единичную силу для определения линейного перемещение, пару сил с моментом равным единице для определения углового перемещения и определить внутренние силовые факторы от единичной силы.

3) Подставить полученные ранее выражения в интеграл Мора и определить перемещение.

Для систем, работающих на изгиб: балок, рам, влияние нормальных сил на величину перемещения незначительно и интеграл Мора в этом случае выглядит:

Источник

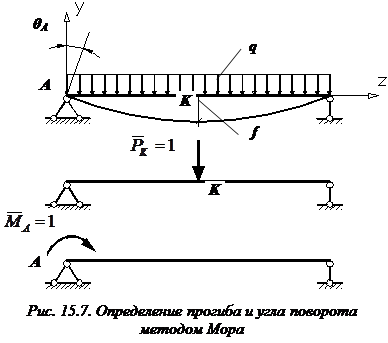
Определение прогибов и углов поворотов методом Мора

Интеграл Мора позволяет определять прогибы и углы поворота заданного сечения балки, используя интегральное исчисление. Хотя данный метод предпочтительнее метода начальных параметров, он неудобен из-за необходимости вычисления интеграла. Из интеграла Мора был получен удобное для практического применения правило Верещагина, при котором не нужно вычислять интегралы, а только нужно находить площадь и центр тяжести эпюр.

Получение формулы интеграла Мора

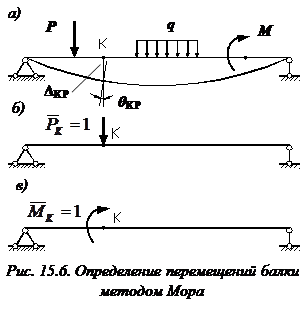
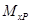
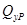
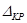
Рассмотрим балку, изображенную на рис. 15.6, а. Обозначим и , соответственно, изгибающий момент и поперечную силу, возникающие в заданной балке от действующей на нее группы нагрузок P. Пусть требуется определить прогиб балки () в точке K.

Введем в рассмотрение вспомогательную балку (та же балка, но нагруженная только единичной силой либо единичным изгибающим моментом). Нагрузим ее только одной силой (рис. 15.6, б). Единичную силу приложим в точке K, где нужно определить прогиб.

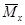
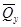
Внутренние усилия, возникающие во вспомогательной балке, обозначим и .

Воспользуемся теперь теоремой о взаимности работ, согласно которой работа внешних сил, приложенных к вспомогательной балке на соответствующих перемещениях заданной балки равна взятой с обратным знаком работе внутренних сил заданной балки на соответствующих перемещениях вспомогательной балки. Тогда .

При определении перемещений в балке, как правило, можно пренебрегать влиянием поперечной силы, ( не учитывать второе слагаемое).

Тогда, учитывая, что , окончательно получим формулу интеграла Мора : .

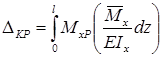
Определение перемещений по формуле интеграла Мора часто называют определением перемещений методом Мора , а саму формулу – интегралом Мора .

Входящие в интеграл Мора изгибающие моменты берутся в произвольном поперечном сечении и поэтому представляют собой аналитические функции от текущей координаты z.

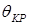
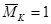
Заметим, что если мы хотим в этой же точке K определить угол поворота поперечного сечения (), то нам необходимо к вспомогательной балке приложить не единичную силу, а единичный момент (рис. 15.6, в).

порядок вычисления перемещений методом Мора:

· к вспомогательной балке в той точке, где требуется определить перемещение, прикладываем единичное усилие. При определении прогиба прикладываем единичную силу , а при определении угла поворота – единичный момент ;

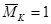
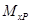
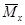
· для каждого участка балки составляем выражения для изгибающих моментов заданной () и вспомогательной () балок;

· вычисляем интеграл Мора для всей балки по соответствующим участкам;

· если вычисленное перемещение имеет положительный знак, то это означает, что его направление совпадает с направлением единичного усилия. Отрицательный знак указывает на то, что действительное направление искомого перемещения противоположно направлению единичного усилия.

Вычисление интеграла Мора пример

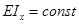
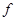
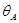
Пусть для шарнирно опертой балки постоянной изгибной жесткости , длиной l, нагруженной равномерно распределенной нагрузкой интенсивностью q (рис. 15.7, а), требуется определить прогиб посредине пролета () и угол поворота на левой опоре ().

определение прогиба с помощью интеграла Мора

В том месте, где нам нужно определить прогиб, к вспомогательной балке прикладываем единичную силу (рис. 15.7, б).

Записываем выражения для изгибающих моментов для каждого из двух участков () заданной и вспомогательной балок:

.

.

Вычисляем интеграл Мора . Учитывая симметрию балки, получим:

.

Определение угла поворота методом Мора

Нагружаем вспомогательную балку единичным моментом , прикладывая его в том месте, где мы ищем угол поворота (рис. 15.7, в).

Записываем выражения для изгибающих моментов в заданной и вспомогательной балках только для одного участка ():

;

.

Тогда интеграл Мора будет иметь вид:

.

Положительный знак в выражении для угла поворота поперечного сечения балки указывает на то, что поворот сечения происходит по направлению единичного момента .

Источник