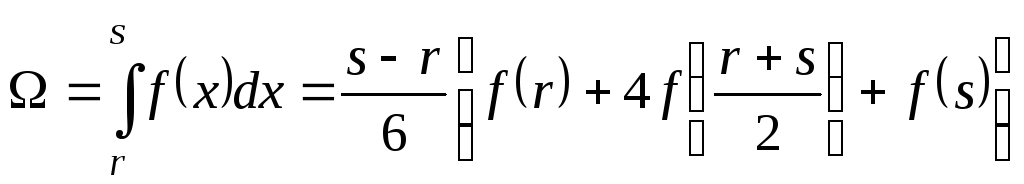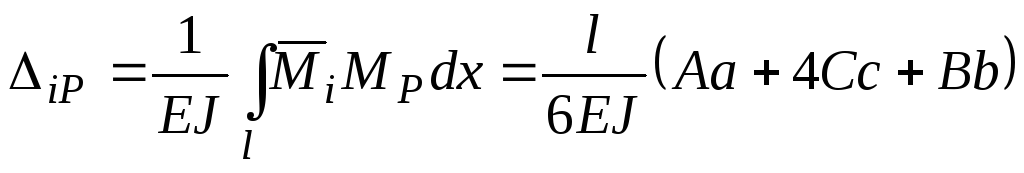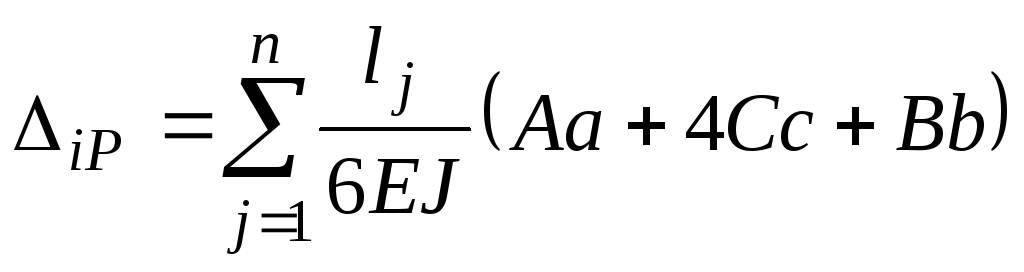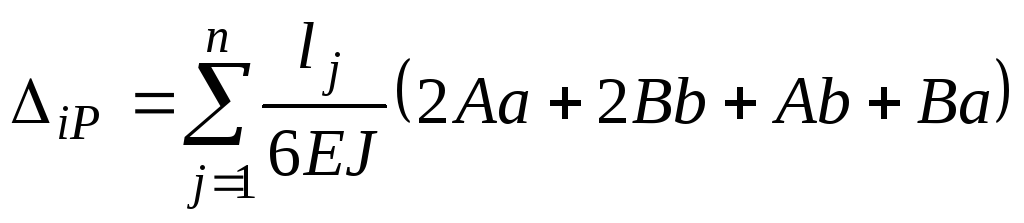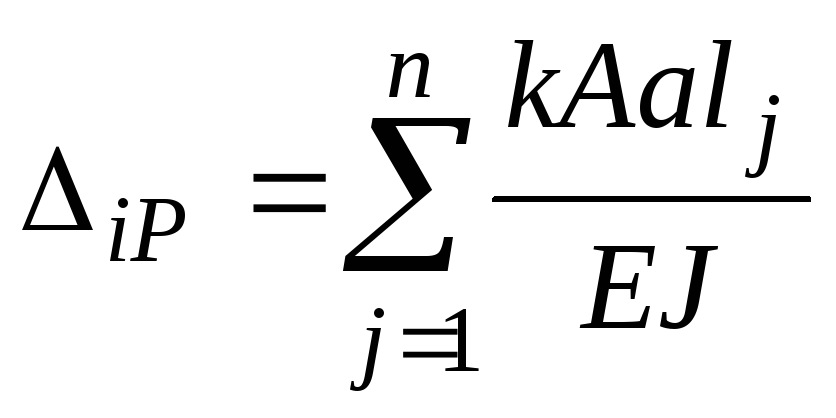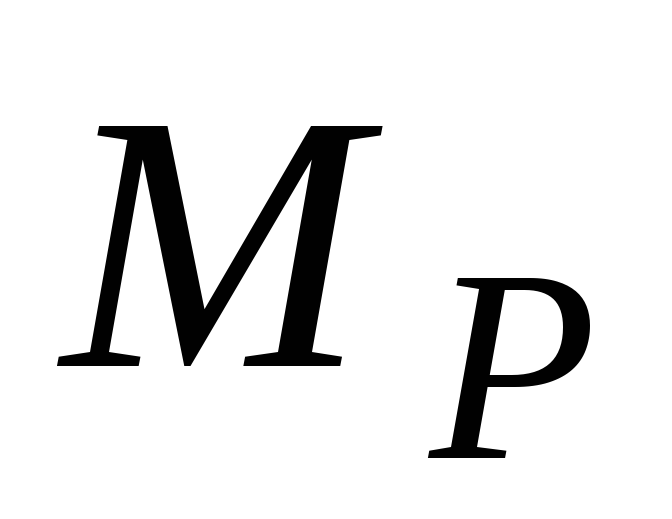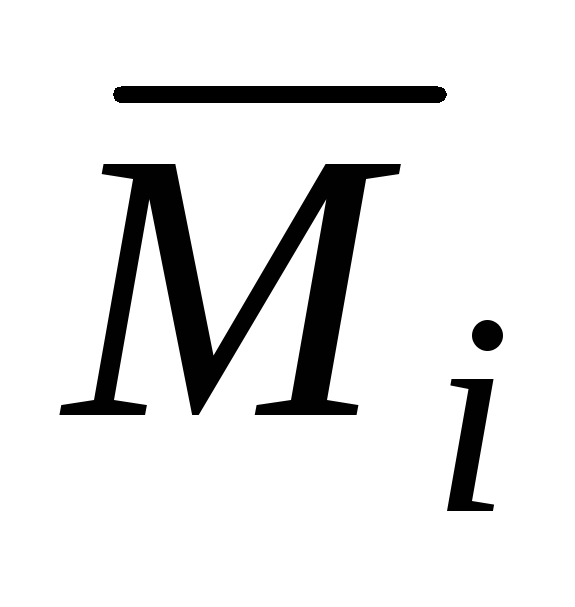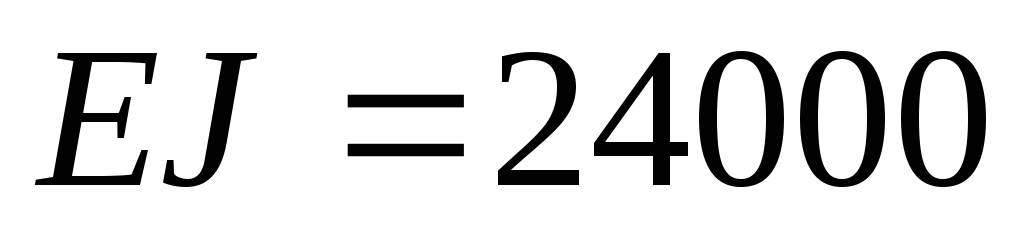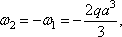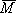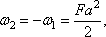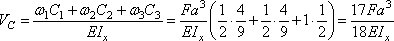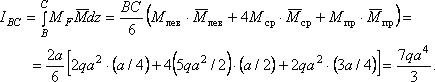Интеграл мора правило верещагина формула симпсона

7.5. Вычисление интегралов Мора по способу Симпсона

Применение метода Мора, как мы уже сумели убедиться, требует вычисления интегралов в процессе определения перемещений. В большинстве случаев при наличии большого числа участков, на которые приходится делить конструкцию, решение становится громоздким. Поэтому в практике расчетов предпочитают иметь дело с графо-аналитическими методами, позволяющими исключить интегрирование из процесса определения перемещений. Такие методы бывают не всегда точны и универсальны, но их простота и доступность делает их весьма популярными. К числу таких методов относится метод Мора-Симпсона. Еще в XVIII веке английским математиком Томасом Симпсоном было предложено вычислять интегралы графическим методом, исходя из того, что интеграл представляет в пределе сумму бесконечно малых величин. Симпсон предложил разбивать площадь фигуры, образовавшуюся под кривой подинтегральной функции, на узкие полоски и суммировать площади этих полосок. Им были сформулированы соответствующие рекомендации и предложены различные формулы, позволяющие упорядочить процесс подобного интегрирования. Сложность этих формул зависела от сложности подинтегрального выражения. В большинстве случаев предложенный им подход к интегрированию дает погрешности, но существуют такие функции, интегрирование которых по способу Симпсона дает точное решение. Речь идет о гладких унимодальных функциях, порядок которых не превышает трех.

Исследуя функции, входящие в формулу Мора, можно сделать вывод, что функции изгибающих моментов, составленных для единичных состояний всегда линейны. При действии на балку распределенной нагрузки постоянной интенсивности изгибающий момент описывается кривой второго порядка. При перемножении этих функций под интегралом Мора мы получаем кривую третьего порядка. Это означает, что, если ограничить класс решаемых задач балками и рамами, нагруженными сосредоточенными силами и распределенной нагрузкой постоянной интенсивности, то при использовании для определения перемещений метода Мора-Симпсона можно получать точное решение.

Рассмотрим интегрирование по способу Симпсона функции, описываемой кубической параболой, приведенной на рис.7.10.

Формула, которой предлагается пользоваться в этом случае, имеет вид:

. (7.32)

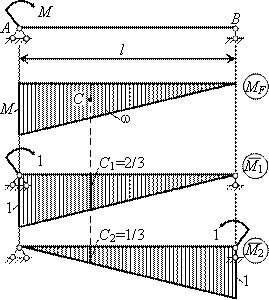
На рис 7.11 приведены грузовая (а) и единичная (б) эпюры изгибающих моментов для одного участка.

Буквами А, С и В обозначены изгибающие моменты на левом конце участка, посредине и на правом конце участка на грузовой эпюре. Буквами а, c и b обозначены изгибающие моменты на левом конце участка, посредине и на правом конце участка на единичной эпюре.

Интеграл Мора для одного участка имеет вид:

. (7.33)

Произведение моментов под интегралом обозначим:

. (7.34)

Применяя формулу Симпсона к интегралу Мора после соответствующих замен и подстановок, получим:

.

При решении задач с несколькими участками формула Мора-Симпсона принимает вид:

. (7.35)

В том случае, если обе эпюры изгибающих моментов, грузовая и единичная, меняются по линейному закону и представляют собой на каждом из участков трапеции, можно исключить средние значения моментов и, учитывая, что они могут быть вычислены из выражений:

; .

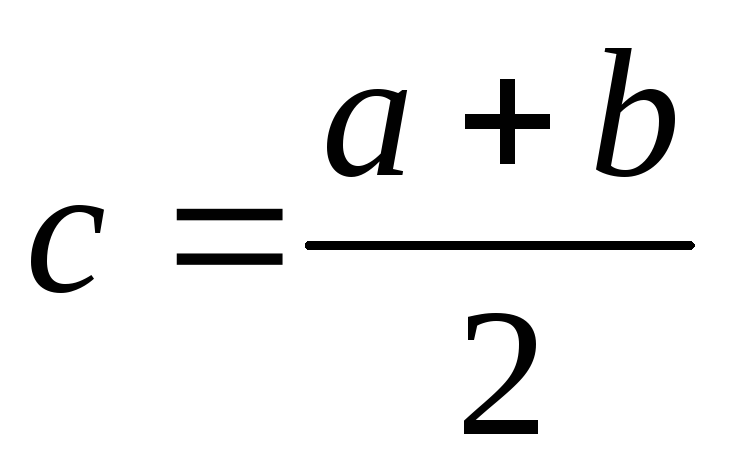
Подставляя эти значения в формулу (7.35), получаем формулу трапеций:

(7.36)

Если обе эпюры представляют собой прямоугольники или треугольники, удобно пользоваться формулой, которая легко получается из формулы (7.35):

(7.37)

Формула (7.37) получила название формулы треугольников. Здесь  коэффициент, величина которого зависит от вида перемножаемых эпюр (Таблица 7.1);  самый большой изгибающий момент на грузовой эпюре;  самый большой изгибающий момент на единичной эпюре;  длина участка. В таблице 7.1 приводятся значения коэффициентов .

Значение коэффициента

Вид эпюры

Вид эпюры

Метод Мора-Симпсона называют методом перемножения эпюр. Рассмотрим порядок решения задач методом Мора-Симпсона.

1. Разбиваем балку на участки и на каждом участке проставляем по три характерных сечения: на левом конце, посредине и на правом конце участка.

2. Вычисляем значения грузовых моментов в каждом из характерных сечений и строим эпюру грузовых изгибающих моментов .

3. Изображаем единичное состояние системы, прикладывая в том сечении, где следует определить перемещение, соответствующую единичную обобщенную силу: при определении прогиба прикладывают сосредоточенную единичную силу; при определении угла поворота прикладывают сосредоточенную единичную пару сил.

4. Вычисляем значения единичных моментов в характерных сечениях и строим эпюру единичных моментов . Эпюр единичных моментов строим столько, сколько следует определить перемещений.

5. Подставляем вычисленные значения грузовых и единичных изгибающих моментов в формулу Мора-Симпсона и вычисляем перемещения.

6. Знак перемещения будет положительным, если искомое перемещение совпадает с направлением соответствующей обобщенной единичной силы. Если направление перемещения и направление обобщенной единичной силы не совпадают, знак перемещения будет отрицательным.

Рассмотрим несколько примеров определения перемещений в стержневых системах по методу Мора-Симпсона.

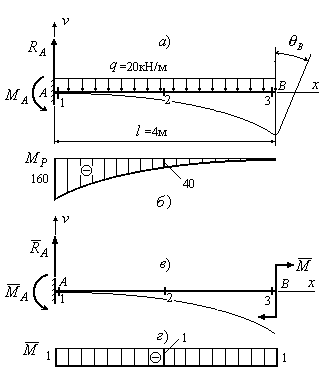
Пример 7.5.Используя метод Мора-Симпсона, определить угол поворота в сечении В изображенной на рис.7.12,а балки, если жесткость поперечного сечения балкикНм 2 .

1. Балка (Рис.7.12,а) содержит один участок. Проставляем характерные сечения и вычисляем в каждом из них грузовые моменты. Значения моментов в характерных сечениях проставлены на рис.7.12,б. Опорные реакции в данной задаче можно не определять, изгибающие моменты можно определить, производя вычисления справа.

2. Строим эпюру грузовых изгибающих моментов .

3. Изображаем единичное состояние балки, прикладывая в сечении В единичный момент (Рис.7.12,в). Находим величины единичных изгибающих моментов в характерных сечениях. Значения этих моментов проставлены на рис.7.12,г.

1. Строим эпюру единичных изгибающих моментов (Рис.7.12,г).

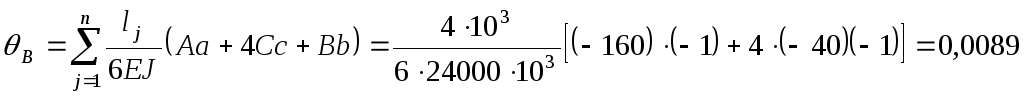
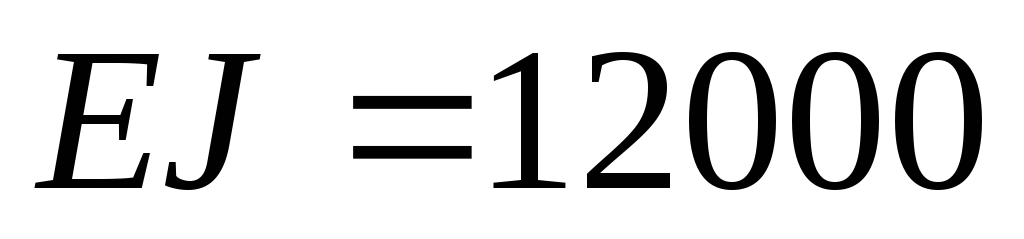
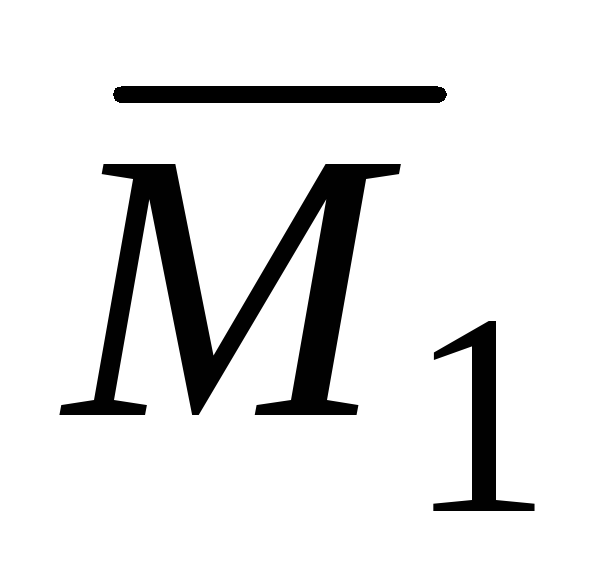
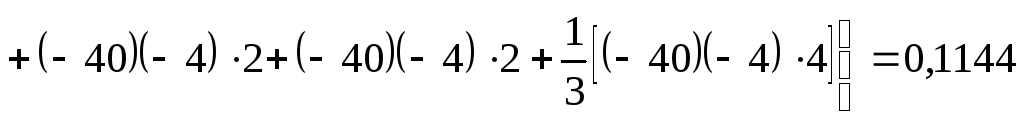
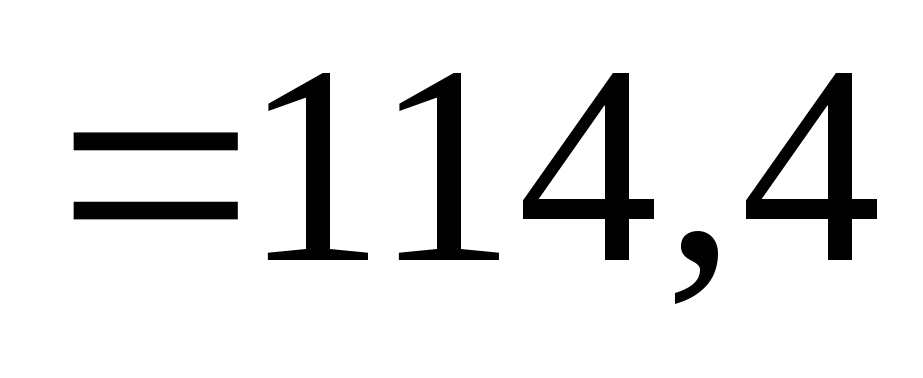
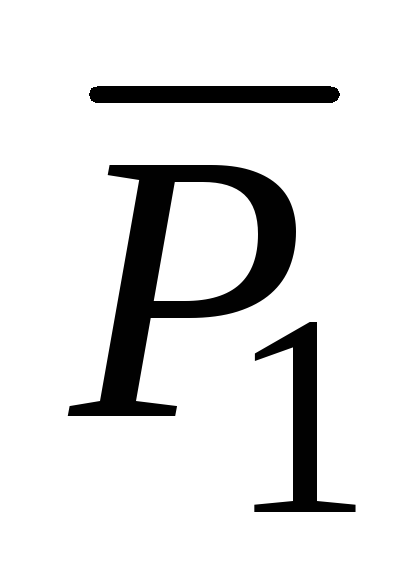
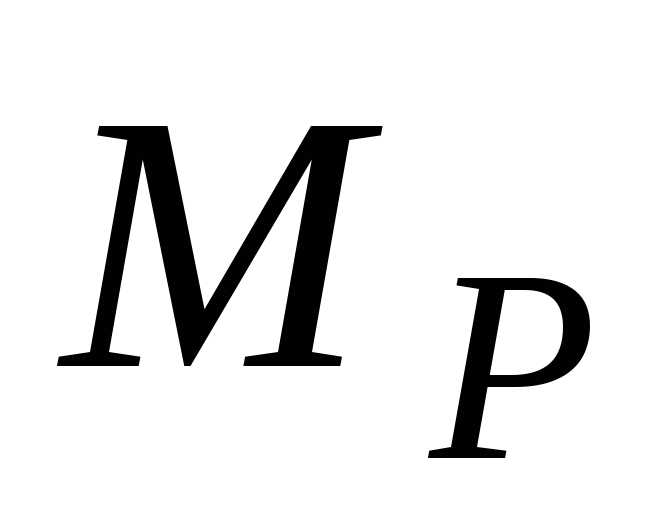
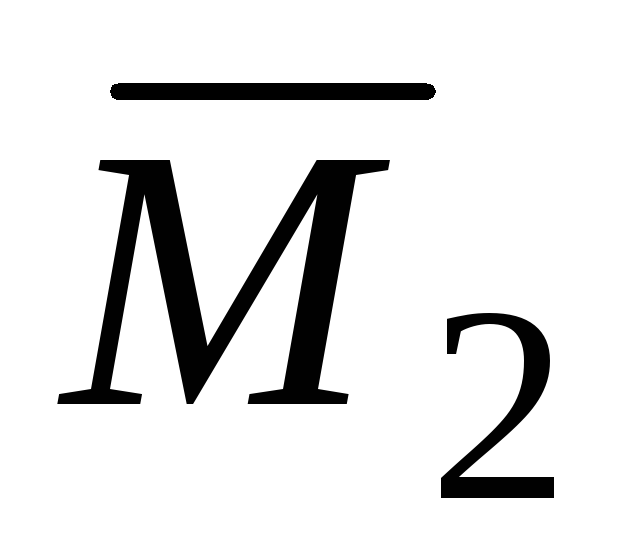
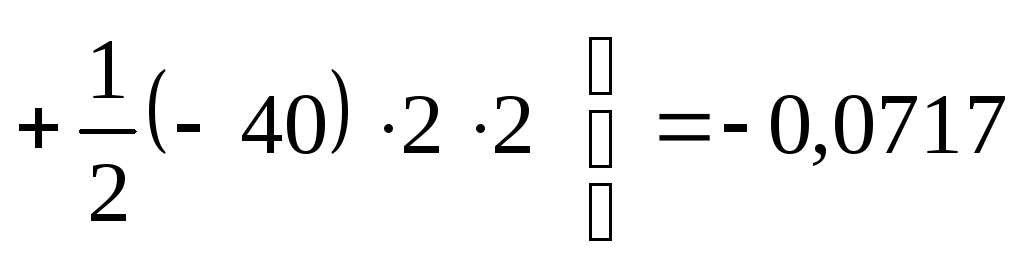
5. Подставляя найденные значения грузовых и единичных изгибающих моментов в формулу Мора-Симпсона (7.35), находим угол поворота сечения В: рад. Пример 7.6.Определить вертикальное и горизонтальное перемещения сечения В рамы, изображенной на рис.7.13,а, если жесткость поперечного сечения рамыкНм 2 . Рис.7.13 Решение: 1. Разбиваем раму на участки, расставляем характерные сечения и выбираем точку наблюдения (Рис.7.13,а). 2. Определяем грузовые моменты в характерных сечениях и строим эпюру грузовых изгибающих моментов (Рис.7.13,б). 3. Изображаем первое единичное состояние (Рис.7.13,в), определяем моменты в характерных сечениях и строим эпюру единичных изгибающих моментов (Рис.7.13,г). 4. Изображаем второе единичное состояние (Рис.7.13,д), определяем моменты в характерных сечениях и строим эпюру единичных изгибающих моментов (Рис.7.13,е). 5. Находим вертикальное перемещения узла В, перемножая эпюры изгибающих моментов и. Поскольку обе эпюры изгибающих моментов являются линейными, при перемножении эпюр воспользуемся формулами трапеций (7.36) и треугольников (7.37). На участке №1 будем перемножать эпюры с помощью формулы трапеций, на участках №2 и №3 – с помощью формулы треугольников: ммм. Перемещение получилось положительным. Это означает, что направление перемещения совпадает с направлением единичной силы . 6. Находим горизонтальное перемещение узла В, перемножая эпюры изгибающих моментов и. Так же, как и в предыдущем пункте будем использовать при перемножении эпюр формулы трапеций и треугольников: ммм. Горизонтальное перемещение оказалось отрицательным. Это означает, что узел В в горизонтальном направлении перемещается не влево, куда изначально была направлена единичная сила, а вправо, что соответствует физическому смыслу задачи.

Источник

Интеграл мора правило верещагина формула симпсона

Калькулятор умножения эпюр объясняет как получить произведение эпюр, необходимое для вычисления интеграла Мора. Обычно используется правило Верещагина или правило Симпсона-Корноухова.
Укажите длину участка и значения по краям эпюр. Для криволинейной эпюры дополнительно укажите интенсивность распределенной нагрузки q («+» вниз, «-» вверх, «0» — если нагрузки нет).
Внизу Вы найдете результат и подробное объяснение, как именно множить Ваши эпюры.

Произведение эпюр по правилу Верещагина

Произведение двух эпюр равно площади первой эпюры, умноженной на значение на второй эпюре напротив центра тяжести первой

$$\int f(z) \cdot y(z) dz =\Omega \cdot y_c $$

В том случае, если площадь или центр тяжести на первой эпюре посчитать сложно, ее обычно разбивают на более простые фигуры.

В нашем случае имеем:
— прямоугольник 6×12, площадь 72, центр тяжести посредине, значение напротив центра тяжести 13;
— треугольник 6×30, площадь 90, центр тяжести на 2/3 длины, значение напротив центра тяжести 3.67;
— парабола 6×54, площадь 216 (высота параболы считается по формуле qL^2/8, и не важно она горизонтально расположена или под углом, а площадь = 2/3 ширины на высоту), центр тяжести посредине, значение напротив центра тяжести 13;
$$\int f(z) = -72\cdot13+90\cdot3.67+216\cdot13=2202$$знак «-» ставим, если первая эпюра и значение на второй расположены по разные стороны стержня.

Произведение эпюр по правилу Симпсона

$$\int f(z) \cdot y(z) dz = \frac< l><6>(y_ \cdot f_+4*y_ \cdot f_+y_ \cdot f_) = $$ $$ = \frac<6><6>(-12\cdot41+4*57\cdot13+18\cdot-15) = 2202$$ где $l$ — длина участка, в скобках $y$ и $f$ — значения на эпюрах слева, посредине участка и справа.

Источник

метод Верещагина

Определить перемещение точки К балки (см. рис.) при помощи интеграла Мора.

1) Составляем уравнение изгибающего момента от внешней силы M_F.

2) Прикладываем в точке К единичную силу F = 1.

3) Записываем уравнение изгибающего момента от единичной силы .

Определить перемещение точки К балки по способу Верещагина.

2) Прикладываем в точке К единичную силу.

; ;

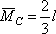
Определить углы поворота на опорах А и В для заданной балки (см. рис.).

Строим эпюры от заданной нагрузки и от единичных моментов, приложенных в сечениях А и В (см. рис.). Искомые перемещения определяем с помощью интегралов Мора

,

, которые вычисляем по правилу Верещагина.

C₁ = 2/3, C₂ = 1/3,

а затем и углы поворота на опорах А и В

Определить угол поворота сечения С для заданной балки (см. рис.).

Определяем опорные реакции R_A=R_B,

, , R_A = R_B = qa.

Строим эпюры изгибающего момента от заданной нагрузки и от единичного момента, приложенного в сечении С, где ищется угол поворота. Интеграл Мора вычисляем по правилу Верещагина. Находим параметры эпюр

C₂ = —C₁ = -1/4,

а по ним и искомое перемещение

.

Определить прогиб в сечении С для заданной балки (см. рис.).

1. Построение эпюр изгибающих моментов.

Эпюра M_F (рис. б)

ВЕ: , ,

, R_B + R_E = F, R_E = 0;

АВ: , R_А = R_В = F; , .

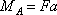
Вычисляем моменты в характерных точках , M_B = 0, M_C = Fa и строим эпюру изгибающего момента от заданной нагрузки.

Эпюра (рис. в).

В сечении С, где ищется прогиб, прикладываем единичную силу и строим от нее эпюру изгибающего момента, вычисляя сначала опорные реакции ВЕ — , , = 2/3; , , = 1/3, а затем моменты в характерных точках , , .

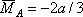
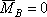
2. Определение искомого прогиба. Воспользуемся правилом Верещагина и вычислим предварительно параметры эпюр и :

,

.

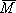
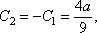
Определить прогиб в сечении С для заданной балки (см. рис.).

Строим эпюры изгибающих моментов от заданной нагрузки и от единичной силы, приложенной в точке С. Пользуясь правилом Верещагина, вычисляем параметры эпюр ,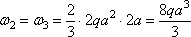

.

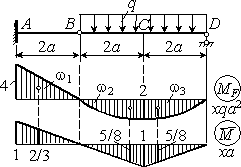
Определить прогиб в сечении С для заданной балки (см. рис.).

1. Построение эпюр изгибающих моментов.

, , R_A = 2qa,

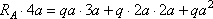
, R_A + R_D = 3qa, R_D = qa.

Строим эпюры изгибающих моментов от заданной нагрузки и от единичной силы, приложенной в точке С.

2. Определение перемещений. Для вычисления интеграла Мора воспользуемся формулой Симпсона, последовательно применяя ее к каждому из трех участков, на которые разбивается балка.

Участок АВ:

Участок ВС:

Участок СD:

.

Определить прогиб сечения А и угол поворота сечения Е для заданной балки (рис. а).

1. Построение эпюр изгибающих моментов.

Эпюра М_F (рис. в). Определив опорные реакции

, , R_B = 19qa/8,

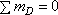
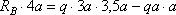
, R_D = 13qa/8, строим эпюры поперечной силы Q и изгибающего момента М_F от заданной нагрузки.

Эпюра (рис. д). В сечении А, где ищется прогиб, прикладываем единичную силу и строим от нее эпюру изгибающего момента.

Эпюра (рис. е). Эта эпюра строится от единичного момента, приложенного в сечении Е, где ищется угол поворота.

2. Определение перемещений. Прогиб сечения А находим, пользуясь правилом Верещагина. Эпюру М_F на участках ВС и CD разбиваем на простые части (рис. г). Необходимые вычисления представляем в виде таблицы.

Источник