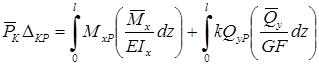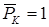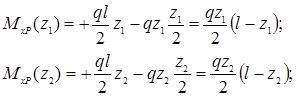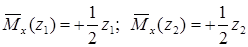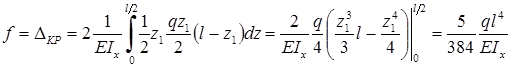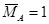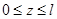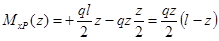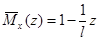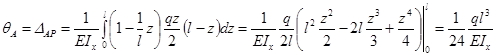Интеграл мора физический смысл

45. Потенциальная энергия бруса в общем случае нагружения.

Общий случай нагружения бруса , когда в поперечных сечениях возникают нормальные и поперечные силы , изгибающие и крутящие моменты одновременно .

При разгрузке тела за счет потенциальной энергии производится работа.

Упругое тело является аккумулятором энергии.

Работа силы на упругом перемещении определяется половиной произведения наибольшего значения силы и перемещения ΔL .

Если бы между силой и перемещением не было прямой пропорциональности, вместо коэффициента ½ был бы получен какой —то другой коэффициент. В частности при постоянной силе он равен единице.

Исключая из полученного для U выражения ΔL, найдем

U = P 2 l/2EF;

Энергия упругих деформаций стержня при изгибе определяется работой момента М на взаимном угловом перемещении dθ двух сечений.

dθ = dz/ρ = Mdz/EJ_x

Если нормальная сила N меняется вдоль оси стержня, то потенциальная энергия деформации должна определяться суммированием по участкам dz. Для элементарного участка dU = N 2 dz /2EF, а для всего стержня

U = L ₀∫ N 2 dz /2EF.

Энергетическое соотношение широко используется при определении перемещения в сложных упругих системах.

Установим теперь метод определения перемещений, основанный на вычислении потенциальной энергии деформации. Поставим задачу нахождения перемещений точек упругой системы по направлению действия приложенных к этой системе внешних сил.

Будем решать эту задачу в несколько приемов; сначала рассмотрим более простой случай (Рис.1), когда на балку в сечениях 1, 2, 3. действуют только сосредоточенные силы , ). и т. д. Под действием этих сил балка прогнется по кривой и останется в равновесии.

Прогибы сечений 1, 2, 3. в которых приложены силы , , . обозначим , , . и т. д. Найдем один из этих прогибов, например — прогиб сечения, в котором приложена сила .

Переведем балку, не нарушая равновесия, из положения в смежное положение , показанное на фиг. 328 пунктиром. Это можно сделать различными приемами: добавить новую нагрузку, увеличить уже приложенные и т. д.

Мы представим себе, что для перехода к смежному деформированному состоянию к силе сделана бесконечно малая добавка (Рис.1); чтобы при этом переходе не нарушать равновесия, будем считать, что эта добавка прикладывается статически, т. е. возрастает от нуля до окончательного значения медленно и постепенно.

Нулевой метод компенсационный( метод измерений) — один извариантов метода сравнения с мерой, в котором на нулевой приборвоздействует сигнал, пропорциональный разности измеряемой и известнойвеличин, причем эту разность доводят до нуля. Пример: измерениеэлектрических величин (электродвижущей силы, электрического сопротивления,емкости и др.) с применением потенциометров и измерительных мостов

Интеграл Мора для случая растяжения-сжатия

Интеграл Мора используется для определения перемещений точек произвольных сечений элементов конструкций. Выведем интеграл Мора для случая растяжения-сжатия. Для простоты рассмотрим стержень постоянной жесткости поперечного сечения, нагруженного сосредоточенной силой F.

Определим перемещение произвольного сечения C стержня, используя теорему Кастилиано. Функция продольной силы для любого сечения этого стержня N=N(F).

Т. к. в точке С отсутствует внешняя сила, использовать напрямую теорему Кастилиано для опредления перемещения нельзя. Поэтому приложим в точке С фиктивную силу Ф.

Функция продольной силы примет вид:

N=N(F)+N₁*Ф

где N₁ – коэффициент пропорциональности.

Определим физический смысл коэффициента N₁. Для этого снимем внешнюю силу F, а фиктивную силу Ф приравняем к единице:

Функция продольной силы при F = 0, Ф = 1 будет равна:

Таким образом, N₁ – это внутренняя продольная сила, возникающая при условии разгрузки элемента конструкции от внешних сил и нагружении в точку, перемещение которой определяется, единичной безразмерной силой.

Потенциальная энергия деформации, в соответствии с формулой (3.1),

Для определения перемещения точки С используем теорему Кастилиано:

Поскольку на самом деле никакой силы в сечении C нет (т.е. Ф=0), то

Это выражение называется интегралом Мора и применяется для определения перемещений точек произвольных сечений элементов конструкций.

Обобщая на k-тое количество участков по N(z) и A(z), перемещение по методу Мора может быть определено:

Суть метод Мора в следующем. Если необходимо определить перемещение в заданной точке по заданному направлению, то наряду с заданной системой внешних сил в этой точке прикладывается внешнее усилие Ф = 1 в интересующим нас направлении.

Далее составляется выражение потенциальной энергии систе­мы, состоящей из n участков с учетом одновременного действия заданной системы внешних сил и силы Ф :

где К_х , К_у  безразмерные величины, зависящие от геометрической формы сечения и учитывают неравномерность распределения касательных напряжений в сечении при поперечном изгибе. Так, например, для прямоугольника К_х = К_у = 1,2, а для двутавра при изгибе в плоскости его стенки K = F/F_CT , где F  площадь всего сечения двутавра, F_CT  площадь стенки; N_z , Q_x , Q_y , M_z , M_x , M_y  внутренние силовые факторы, возникающие в поперечных сечениях заданной стержневой системы; внутренние силовые факторы, возникающие в поперечных сечениях заданной системы, от действия усилия Ф = 1.

Дифференцируя выражение (6.1) по Ф, и полагая после этого Ф = 0, находим искомое перемещение в искомой точке в нужном направлении.

Источник

Определение прогибов и углов поворотов методом Мора

Интеграл Мора позволяет определять прогибы и углы поворота заданного сечения балки, используя интегральное исчисление. Хотя данный метод предпочтительнее метода начальных параметров, он неудобен из-за необходимости вычисления интеграла. Из интеграла Мора был получен удобное для практического применения правило Верещагина, при котором не нужно вычислять интегралы, а только нужно находить площадь и центр тяжести эпюр.

Получение формулы интеграла Мора

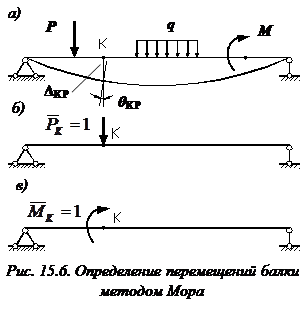
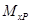
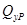
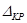
Рассмотрим балку, изображенную на рис. 15.6, а. Обозначим и , соответственно, изгибающий момент и поперечную силу, возникающие в заданной балке от действующей на нее группы нагрузок P. Пусть требуется определить прогиб балки () в точке K.

Введем в рассмотрение вспомогательную балку (та же балка, но нагруженная только единичной силой либо единичным изгибающим моментом). Нагрузим ее только одной силой (рис. 15.6, б). Единичную силу приложим в точке K, где нужно определить прогиб.

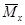
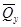
Внутренние усилия, возникающие во вспомогательной балке, обозначим и .

Воспользуемся теперь теоремой о взаимности работ, согласно которой работа внешних сил, приложенных к вспомогательной балке на соответствующих перемещениях заданной балки равна взятой с обратным знаком работе внутренних сил заданной балки на соответствующих перемещениях вспомогательной балки. Тогда .

При определении перемещений в балке, как правило, можно пренебрегать влиянием поперечной силы, ( не учитывать второе слагаемое).

Тогда, учитывая, что , окончательно получим формулу интеграла Мора : .

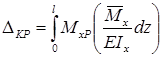
Определение перемещений по формуле интеграла Мора часто называют определением перемещений методом Мора , а саму формулу – интегралом Мора .

Входящие в интеграл Мора изгибающие моменты берутся в произвольном поперечном сечении и поэтому представляют собой аналитические функции от текущей координаты z.

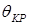
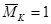
Заметим, что если мы хотим в этой же точке K определить угол поворота поперечного сечения (), то нам необходимо к вспомогательной балке приложить не единичную силу, а единичный момент (рис. 15.6, в).

порядок вычисления перемещений методом Мора:

· к вспомогательной балке в той точке, где требуется определить перемещение, прикладываем единичное усилие. При определении прогиба прикладываем единичную силу , а при определении угла поворота – единичный момент ;

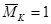
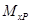
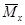
· для каждого участка балки составляем выражения для изгибающих моментов заданной () и вспомогательной () балок;

· вычисляем интеграл Мора для всей балки по соответствующим участкам;

· если вычисленное перемещение имеет положительный знак, то это означает, что его направление совпадает с направлением единичного усилия. Отрицательный знак указывает на то, что действительное направление искомого перемещения противоположно направлению единичного усилия.

Вычисление интеграла Мора пример

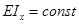
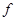
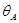
Пусть для шарнирно опертой балки постоянной изгибной жесткости , длиной l, нагруженной равномерно распределенной нагрузкой интенсивностью q (рис. 15.7, а), требуется определить прогиб посредине пролета () и угол поворота на левой опоре ().

определение прогиба с помощью интеграла Мора

В том месте, где нам нужно определить прогиб, к вспомогательной балке прикладываем единичную силу (рис. 15.7, б).

Записываем выражения для изгибающих моментов для каждого из двух участков () заданной и вспомогательной балок:

.

.

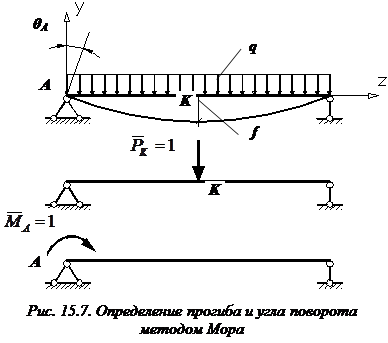
Вычисляем интеграл Мора . Учитывая симметрию балки, получим:

.

Определение угла поворота методом Мора

Нагружаем вспомогательную балку единичным моментом , прикладывая его в том месте, где мы ищем угол поворота (рис. 15.7, в).

Записываем выражения для изгибающих моментов в заданной и вспомогательной балках только для одного участка ():

;

.

Тогда интеграл Мора будет иметь вид:

.

Положительный знак в выражении для угла поворота поперечного сечения балки указывает на то, что поворот сечения происходит по направлению единичного момента .

Источник

Большая Энциклопедия Нефти и Газа

Физический смысл интегралов Ариса можно описать лишь весьма приближенно; однако всегда полезно наглядно представить себе факторы, входящие в выражение для высоты, эквивалентной теоретической тарелке. Грубо говоря, интегрирование по t дает время, которое возрастает с увеличением размеров колонки. Это можно объяснить тем, что при увеличении размеров колонки возрастают расстояния, вдоль которых диффундируют молекулы. Однако, несмотря на это, действительное значение Н ( х) определяется эффективной скоростью, значение которой в свою очередь определяется профилем скоростей. [6]

Обратим внимание на физический смысл интегралов в этом уравнении. Первый интеграл выражает уменьшение секундного расхода через сечение в пограничном слое высотой 8, обусловленное влиянием вязкости. [7]

Для последующего вывода необязательно дать физический смысл Зтого интеграла , но легко сообразить, что он выражает удвоенную работу внешних нагрузок в процессе деформации тела, если эти нагрузки возрастают весьма медленно от начального естественного состояния тела. [8]

Рассмотрим теперь более подробно природу и физический смысл интегралов такого рода. [9]

Цель работы состоит в изучении основных явлений, демонстрирующих общие законы динамики системы точек и физический смысл интегралов движения . В общем случае задача нелинейна, и получить ее аналитическое решение не удается. В то же время проведение серии машинных экспериментов позволяет составить достаточно полное и наглядное представление об особенностях движения изучаемой механической системы. Специфика постановки машинного эксперимента проявляется, во-первых, в необходимости предварительной оценки характерного времени протекания процессов для правильной организации вывода результатов решения задачи. Эта оценка определяется заданием конкретных значений параметров системы и начальных условий и проводится студентом предварительно перед каждым вводом исходных данных. Во-вторых, некорректное задание параметров или начальных условий может приводить к аварийным прерываниям решения, не связанным с существом задачи и определяемым ее конкретной реализацией на машине. Студенты убеждаются также, что точность решения зависит как от выбора алгоритма, так и от исходных данных. Нетрудно проследить, например, как изменяют свое численное значение интегралы движения, если выбран сравнительно крупный шаг интегрирования дифференциальных уравнений. [10]

Вместе с тем, для многих приложе ний наиболее существенна именно / Атеория, что, в частности, объясняется физическим смыслом интеграла от квадрата модуля. [11]

При этом существование предела ( 4) для конечной функции, заданной на конечной области, может быть доказано математически, без ссылки на физический смысл интеграла . [12]

На рис. 1 а и 1, б изображены типичные примеры; на рис. 1, в показано, что две кривые могут быть зацеплены даже когда коэффициент зацепления равен нулю, а соленоид на рис. 1 г демонстрирует физический смысл интеграла Гаусса как работы по переносу единичного магнитного полюса по замкнутой кривой в магнитном поле, вызванном протеканием единичного электрического тока по другой кривой. [13]

Формула (2.27) представляет собой модифицированный принцип Гюйгенса — Френеля в нелинейной оптике. Физический смысл интеграла (2.27) довольно прост. [14]

Возможны дальнейшие обобщения интеграла Мора, когда прикладывается не единичный силовой фактор, а единичная система сил. Физический смысл интеграла Мора вытекает на того, что он представляет возможную работу единичной системы сил на перемещениях основной системы. [15]

Источник