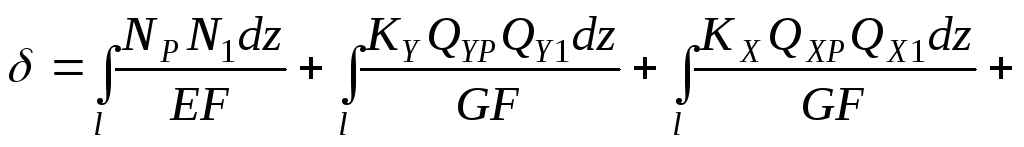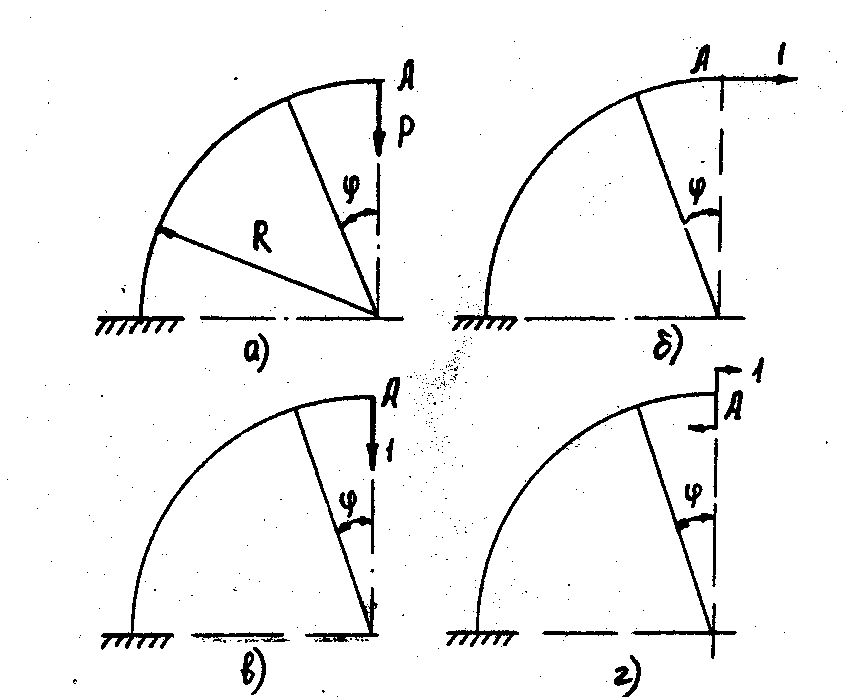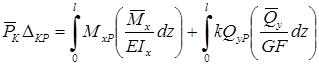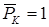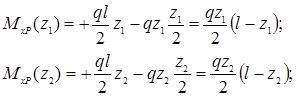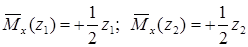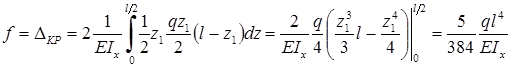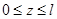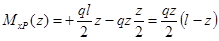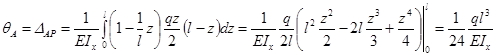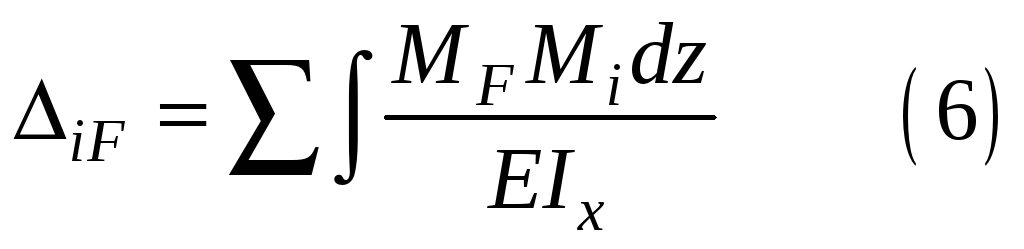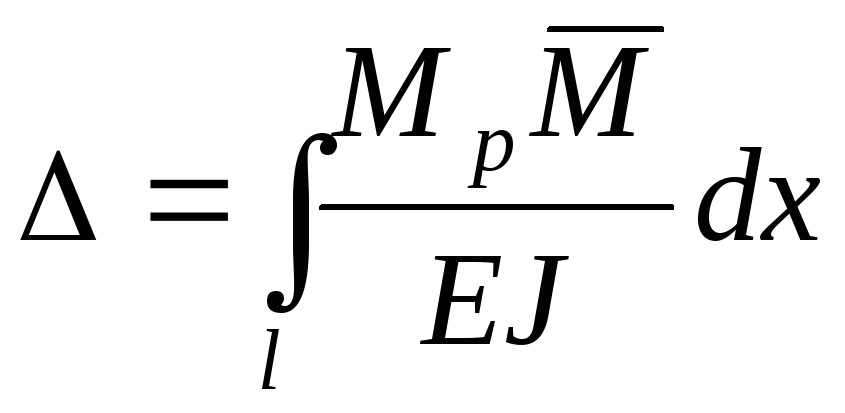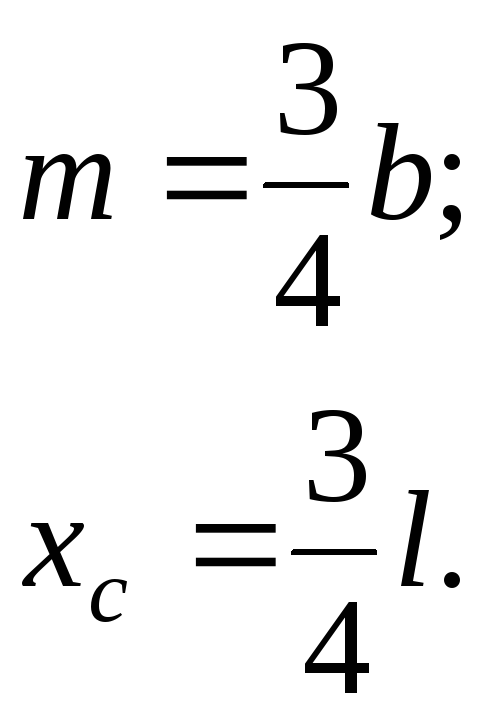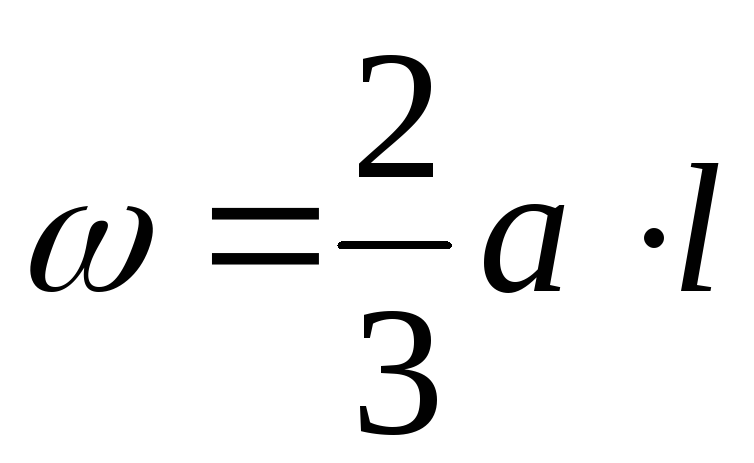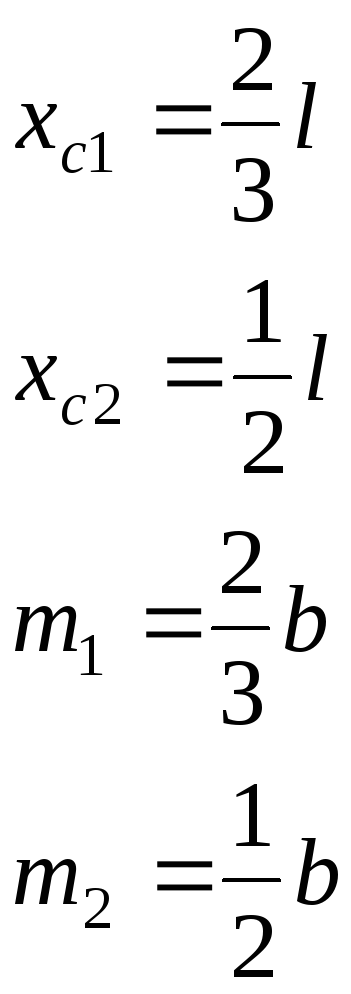Интеграл мора его использования

6.2.2. Интеграл Мора

Непосредственно по теореме Кастилиано можно определить перемещение только в том случае, если тело нагружено соответствующей этому перемещению обобщенной силой. Однако, эта трудность легко преодолима. Если требуется определить перемещение в точке, где не приложено внешних сил, можно приложить в этой точке силу Ф, соответствующую определяемому перемещению. Написав далее выражение потенциальной энергии тела в зависимости от всех действующих на тело нагрузок и силы Ф, возьмем частную производную от этой энергии по Ф. В полученном выражении для перемещения необходимо положить силу Ф равной нулю.

Вернемся к рассмотрению стержня. Для определения перемещения некоторой точки стержня приложим в этой точке соответствующую этому перемещению обобщенную силу Ф (если определяется линейное перемещение, то прикладывается сила, если угловое, – то момент). При этом внутренние силовые факторы в различных поперечных сечениях изменятся на величины, зависящие от Ф. Например, крутящий момент, возникающий в стержне под действием приложенных к нему нагрузок, окажется равным М_КР + М_КФ, где первое слагаемое определяет момент, возникающий в стержне под действием приложенных к нему нагрузок, а второе слагаемое – дополнительный момент, возникающий при приложении силы Ф. Очевидно, что момент М_КФ пропорционален силе Ф. Поэтому можем записать

где М_К1— коэффициент пропорциональности.

Следовательно, крутящий момент

Если снять с бруса все нагрузки и положить Ф = 1, то М_К = М_К1, откуда следует, что М_К1 – это крутящий момент, возникающий в брусе при его нагружении единичной (т.е. равной единице) силой, приложенной в точке и по направлению, соответствующим определяемому перемещению.

Аналогичное справедливо и относительно других внутренних силовых факторов. Это позволяет записать выражение потенциальной энергии стержня при действии на него нагрузок и силы Ф

.

Здесь N_P, Q_YP, … — внутренние силовые факторы, возникающие в стержне под действием приложенных к нему нагрузок (без силы Ф), а N₁, Q_Y1, … — внутренние силовые факторы, возникающие при нагружении стержня единичной силой.

Определим теперь искомое перемещение δ, взяв частную производную от потенциальной энергии по Ф и положив в полученном выражении Ф = 0

. (6.9)

Полученную формулу называют интегралом Мора. Эта формула была получена Мором без использования теоремы Кастилиано из геометрических соображений.

Не все слагаемые формулы (6.9) равнозначны. Обычно слагаемые, связанные с силами N, Q_Y, Q_Х малы по сравнению со слагаемыми, зависящими от моментов М_К, М_Х, М_Y. Свидетельством этому являет пример в п. 6.2.1. Поэтому, например, в случае изгиба обычно определяют перемещение, пренебрегая влиянием поперечной силы на эти перемещения. Правило знаков здесь аналогично правилу знаков при использовании теоремы Кастилиано: если перемещение получено со знаком «плюс», то это означает, что оно происходит в направлении единичной силы.

Пример. Определим горизонтальное и вертикальное перемещение и поворот сечения А криволинейного стержня, показанного на рис. 6.7.

Изгибающий момент в сечении, положение которого определено полярной координатой φ, равен

.

Для определения горизонтального перемещения сечения А приложим в этом сечении горизонтальную единичную силу (рис. 6.7, б). Изгибающий момент от этой силы

.

.

Для определения вертикального перемещения y_A приложим в сечении А вертикальную единичную силу (рис. 6.7, в). Ее момент

.

.

И, наконец, для определения угла поворота Θ_А сечения А необходимо приложить единичный момент (рис. 6.7, г). Очевидно, в этом случае М₁ = 1. Поэтому

.

Источник

Определение прогибов и углов поворотов методом Мора

Интеграл Мора позволяет определять прогибы и углы поворота заданного сечения балки, используя интегральное исчисление. Хотя данный метод предпочтительнее метода начальных параметров, он неудобен из-за необходимости вычисления интеграла. Из интеграла Мора был получен удобное для практического применения правило Верещагина, при котором не нужно вычислять интегралы, а только нужно находить площадь и центр тяжести эпюр.

Получение формулы интеграла Мора

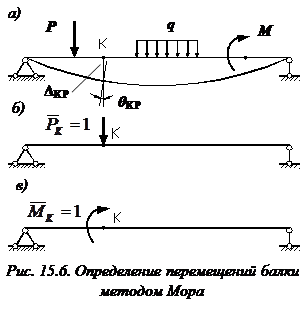
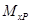
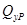
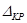
Рассмотрим балку, изображенную на рис. 15.6, а. Обозначим и , соответственно, изгибающий момент и поперечную силу, возникающие в заданной балке от действующей на нее группы нагрузок P. Пусть требуется определить прогиб балки () в точке K.

Введем в рассмотрение вспомогательную балку (та же балка, но нагруженная только единичной силой либо единичным изгибающим моментом). Нагрузим ее только одной силой (рис. 15.6, б). Единичную силу приложим в точке K, где нужно определить прогиб.

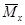
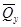
Внутренние усилия, возникающие во вспомогательной балке, обозначим и .

Воспользуемся теперь теоремой о взаимности работ, согласно которой работа внешних сил, приложенных к вспомогательной балке на соответствующих перемещениях заданной балки равна взятой с обратным знаком работе внутренних сил заданной балки на соответствующих перемещениях вспомогательной балки. Тогда .

При определении перемещений в балке, как правило, можно пренебрегать влиянием поперечной силы, ( не учитывать второе слагаемое).

Тогда, учитывая, что , окончательно получим формулу интеграла Мора : .

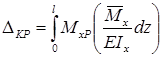
Определение перемещений по формуле интеграла Мора часто называют определением перемещений методом Мора , а саму формулу – интегралом Мора .

Входящие в интеграл Мора изгибающие моменты берутся в произвольном поперечном сечении и поэтому представляют собой аналитические функции от текущей координаты z.

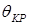
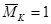
Заметим, что если мы хотим в этой же точке K определить угол поворота поперечного сечения (), то нам необходимо к вспомогательной балке приложить не единичную силу, а единичный момент (рис. 15.6, в).

порядок вычисления перемещений методом Мора:

· к вспомогательной балке в той точке, где требуется определить перемещение, прикладываем единичное усилие. При определении прогиба прикладываем единичную силу , а при определении угла поворота – единичный момент ;

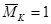
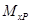
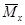
· для каждого участка балки составляем выражения для изгибающих моментов заданной () и вспомогательной () балок;

· вычисляем интеграл Мора для всей балки по соответствующим участкам;

· если вычисленное перемещение имеет положительный знак, то это означает, что его направление совпадает с направлением единичного усилия. Отрицательный знак указывает на то, что действительное направление искомого перемещения противоположно направлению единичного усилия.

Вычисление интеграла Мора пример

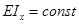
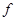
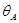
Пусть для шарнирно опертой балки постоянной изгибной жесткости , длиной l, нагруженной равномерно распределенной нагрузкой интенсивностью q (рис. 15.7, а), требуется определить прогиб посредине пролета () и угол поворота на левой опоре ().

определение прогиба с помощью интеграла Мора

В том месте, где нам нужно определить прогиб, к вспомогательной балке прикладываем единичную силу (рис. 15.7, б).

Записываем выражения для изгибающих моментов для каждого из двух участков () заданной и вспомогательной балок:

.

.

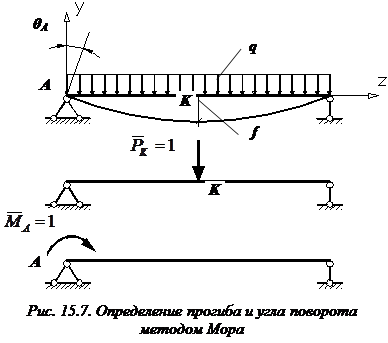
Вычисляем интеграл Мора . Учитывая симметрию балки, получим:

.

Определение угла поворота методом Мора

Нагружаем вспомогательную балку единичным моментом , прикладывая его в том месте, где мы ищем угол поворота (рис. 15.7, в).

Записываем выражения для изгибающих моментов в заданной и вспомогательной балках только для одного участка ():

;

.

Тогда интеграл Мора будет иметь вид:

.

Положительный знак в выражении для угла поворота поперечного сечения балки указывает на то, что поворот сечения происходит по направлению единичного момента .

Источник

Метод Мора. Интеграл Мора

Теорема Кастельяно дала нам возможность определять перемещения. Эту теорему используют для отыскания перемещений в пластинках, оболочках. Однако, вычисление потенциальной энергии громоздкая процедура и мы сейчас наметим более простой и наиболее общий путь определения перемещений в стержневых системах.

Пусть задана произвольная стержневая система и нам нужно определить в ней перемещение точки по направлению , вызванное всеми силами системы —

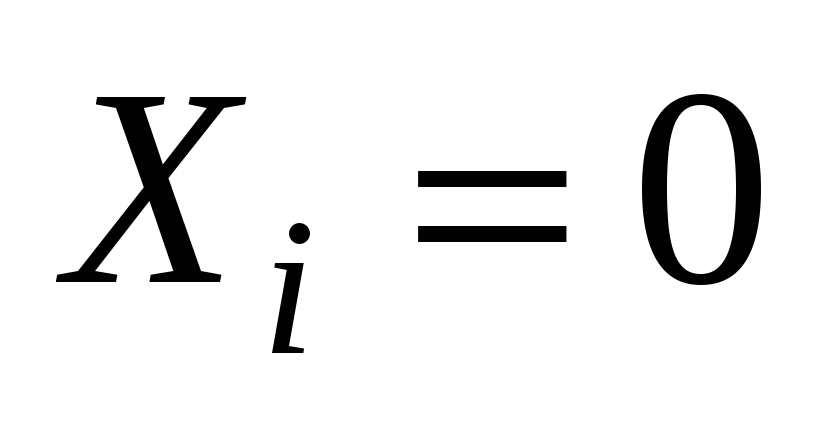
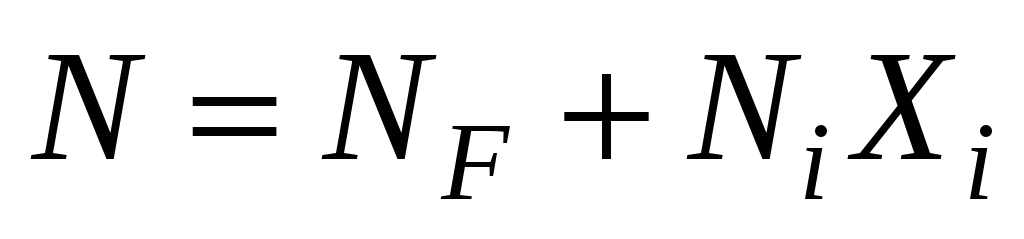
Т.к. в общем случае в системе нет силы, приложенной по направлению искомого перемещения, то воспользоваться теоремой Кастельяно нельзя. Добавим к числу прочих сил силу , приложенную к точке и действующую в направлении . Тогда внутренние силовые факторы в системе можно выразить

, где — внутренние силовые факторы в системе от действующих сил;

— внутренние силовые факторы от силы .

Внесем эти выражения в (3)

По теореме Кастельяно:

Учтя, что

получаем выражение:

называемое интегралом Мора.

Для того, чтобы определить перемещение с помощью метода Мора, необходимо:

1) Определить внутренние силовые факторы в системе от заданных сил.

2) Приложить по направлению искомого перемещения единичную обобщенную силу (единичную силу для определения линейного перемещение, пару сил с моментом равным единице для определения углового перемещения и определить внутренние силовые факторы от единичной силы.

3) Подставить полученные ранее выражения в интеграл Мора и определить перемещение.

Для систем, работающих на изгиб: балок, рам, влияние нормальных сил на величину перемещения незначительно и интеграл Мора в этом случае выглядит:

Источник

2. Правило Мора-Верещагина (графический способ вычисления интеграла Мора)

Кроме метода начальных параметров существует эффективный универсальный метод определения перемещений в балках, рамах и упругих конструкциях произвольной конфигурации – метод Мора. Упругое перемещение (либо прогиб, либо угол поворота сечения) определяется по формуле:

, (1.3)

где – изгибающий момент от заданной нагрузки;– изгибающий момент от единичной силы, приложенной в той точке, в которой определяется перемещение.

Упрощение операций интегрирования возможно для конструкций с прямолинейной осью постоянной жесткости и основано на том, что эпюры от единичных усилий на прямолинейных участках оказываются линейными. Рассматривая эту процедуру применительно к участку балки, преобразуем интеграл Мора с учетом этой особенности. На рис. 1.3 сверху показан участок балки с эпюрой общего вида, а внизу эпюра , представляющая собой линейную функцию. В результате несложного расчета (подробности смотри в учебнике) установлено, что интеграл произведения двух функций и численно равен площади эпюры , умноженной на величину момента, взятого с эпюры в сечении, соответствующем центру тяжести эпюры .

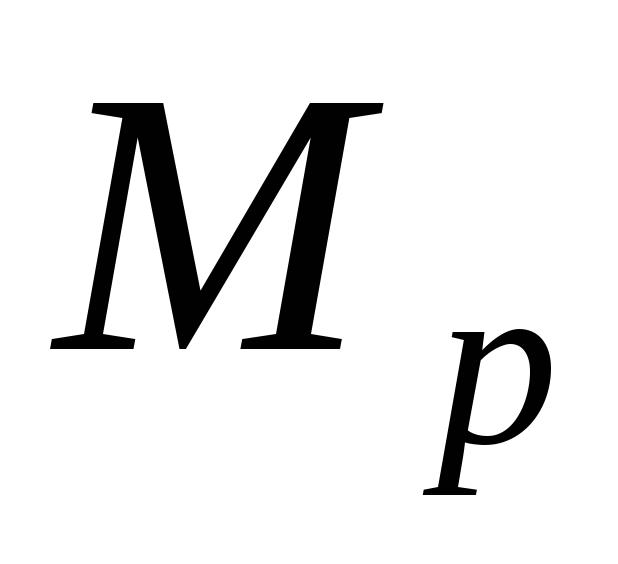
. (1.4)

Если балка имеет несколько участков по длине, формула Верещагина будет иметь вид

, (1.5)

где – площадь эпюры моментов от внешней нагрузки (грузовой эпюры); – ордината единичной эпюры под центром тяжести грузовой эпюры; – число участков по длине балки.

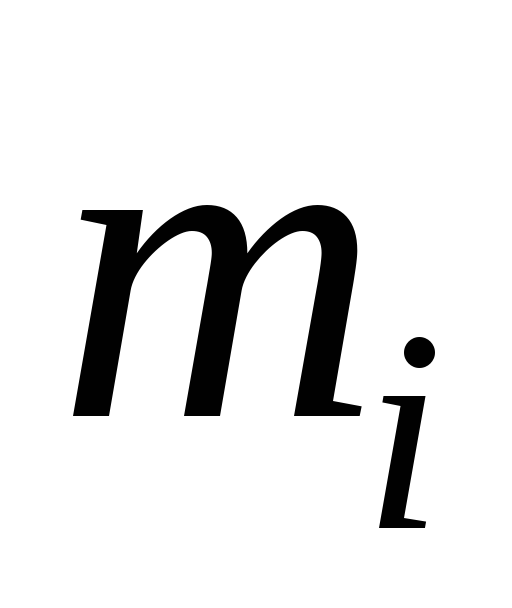
При пользовании этой формулой надо уметь вычислять площади и координаты центров тяжести основных фигур: прямоугольника, прямолинейного треугольника и криволинейного треугольника. Минимально необходимые справочные данные приведены в табл. 1.1. Процедуру графического вычисления называют «перемножением» эпюр.

Эпюры и

эпюры ,

тяжести

Эпюры и

эпюры ,

тяжести

Примечания: 1. Все кривые в табл. 1.1 – квадратные параболы. 2. При «перемножении» эпюр одного знака их произведение положительно. 3. При «перемножении» эпюр разных знаков их произведение отрицательно.

В случае, если эпюра тоже линейная, операция перемножения обладает свойством коммутативности: безразлично, умножается ли площадь грузовой эпюры на ординату единичной или площадь единичной на ординату грузовой.

Рассмотрим на примере расчетной схемы, показанной на рис. 1.4, порядок решения задач при определении перемещения с помощью правила Мора-Верещагина. Определим прогиб в точке .

Чтобы построить эпюры и ,можно не определять опорные реакции: достаточно сосчитать момент на опореот нагрузки на консоли, построить эпюру на консоли, а затем соединить прямой линией значениеM на опореB с нулем на опореA.

В соответствии с формулой (1.5)

.

Источник