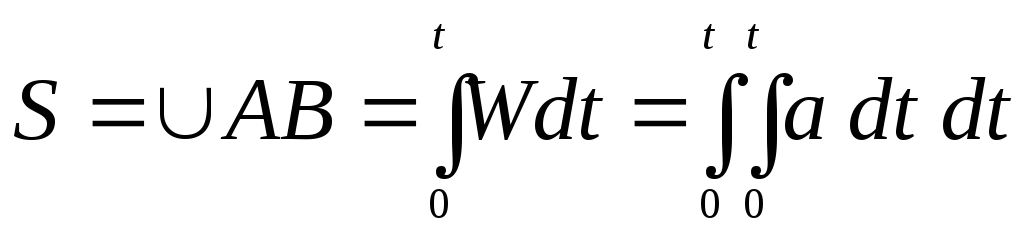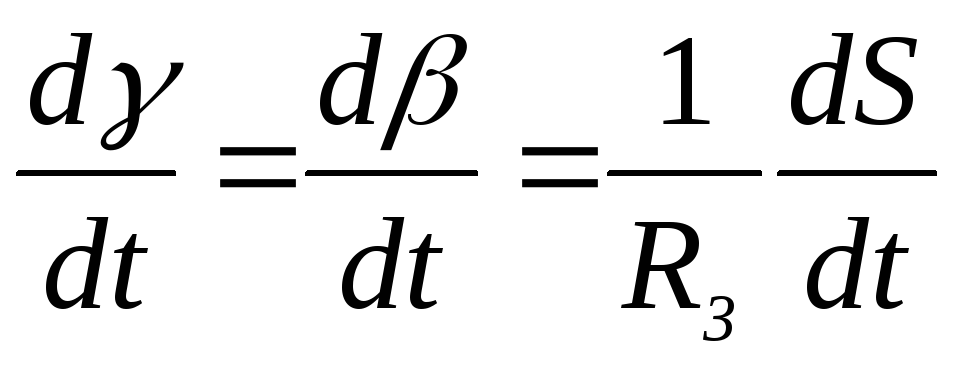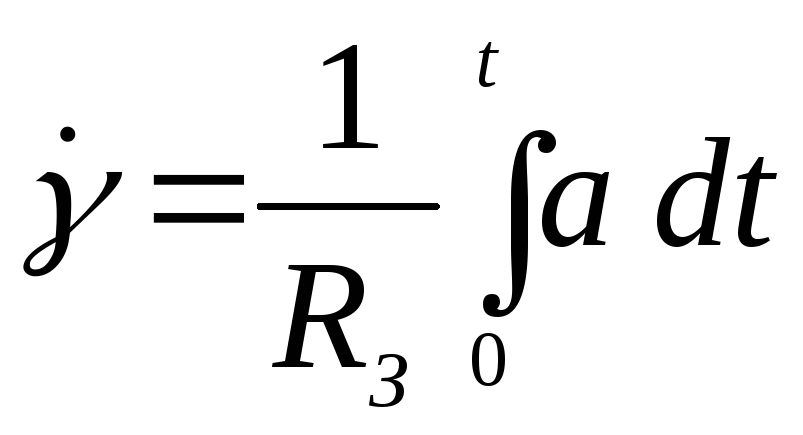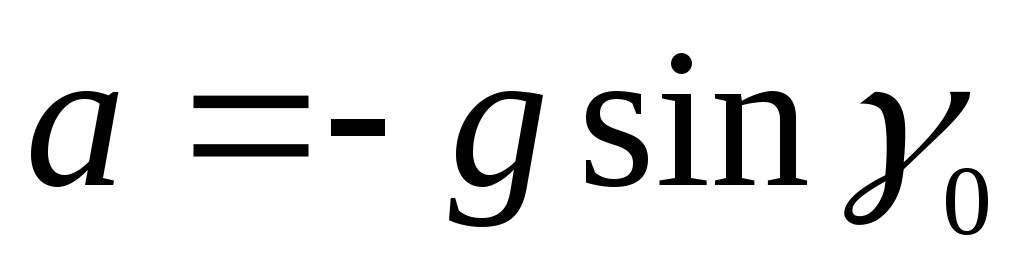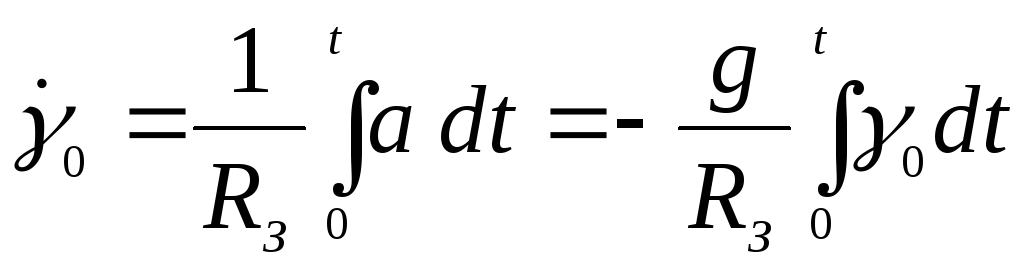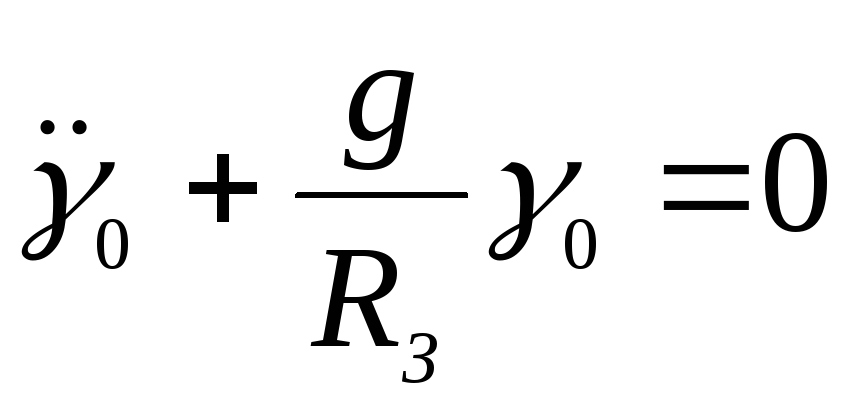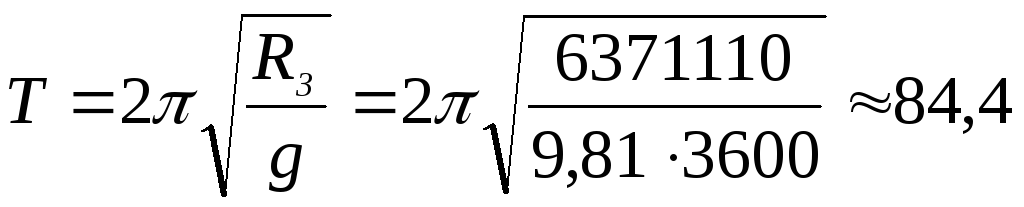Инерциальные навигационные системы морских объектов

Раздел 7. Инерциальные навигационные системы

7.5. Бесплатформенная инерциальная навигационная система И42-1С.

7.1. Особенности инерциальных навигационных систем

Инерциальные навигационные системы (ИНС) – это точные автоматические устройства, основанные на применении измерителей ускорений (акселерометров), стабилизаторов для удержания акселерометров в определенном положении относительно инерционной системы координат (ИСК), счетно-решающих устройств для вычисления местоположения летальных аппаратов и указывающих приборов.

ИНС по способу определения координат местонахождения летательного аппарата относятся к системам счисления пути. Они используются для решения следующих навигационных задач:

– непрерывного измерения с помощью акселерометров ускорений центра масс ЛА под действием активных (негравитационных) сил;

– моделирования навигационных систем координат (НСК);

– вычисления составляющих скорости путем однократного интегрирования и координат местонахождения центра масс ЛА путем двухкратного интегрирования измеренных ускорений;

– измерения углов ориентации ЛА относительно ИСК (углов сноса и скольжения, углов крена, курса и тангажа).

ИНС имеют перед другими навигационными системами важные преимущества – универсальность применения, возможность определения основных параметров движения (координаты местонахождения, скорость, ускорение, направление движения, пространственная ориентация, т.е. угловое положение в заданной системе координат в пространстве, угловая скорость и др.), автономность действия, помехозащищенность, высокая точность при ограничении времени действия.

ИНС присущи определенные недостатки, главными из которых являются: возрастание погрешностей с течением времени, что ограничивает возможность использования во времени без применения корректирующих средств; сложность устройства и необходимость применения высокопрецизионных базовых измерительных элементов и вычислительных устройств, высокая стоимость в эксплуатации.

7.2. Принципы определения текущих координат, скорости ла и построения вертикали в инс

Рассмотрим движение ЛА в одной плоскости вокруг неподвижной Земли, имеющей форму шара. На горизонтальной платформе поместим акселерометр. Пусть ЛА, сохраняя горизонтальность движения в течение времени , перемещается из точкив точку(рис. 7.1,а). Тогда интегратор, на вход которого подается сигнал, пропорциональный, т.е. величине путевой скорости ЛА. Если выход первого интеграторасоединить со входом второго интегратора(рис. 7.1,б), то на выходе последнего появится сигнал, пропорциональный пути, пройденному ЛА за время интегрирования:

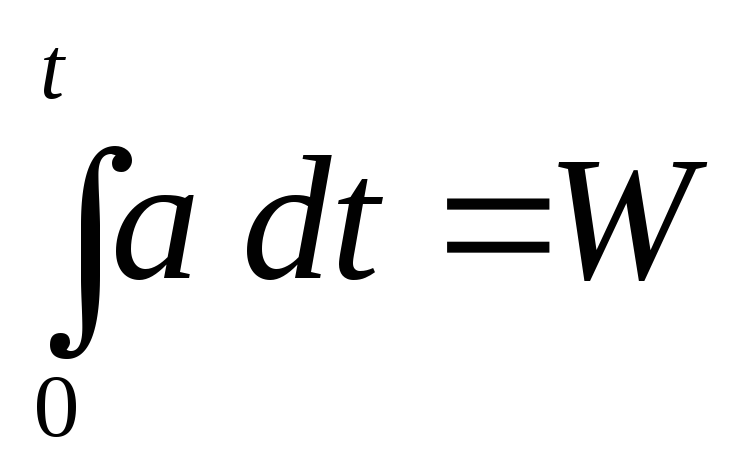
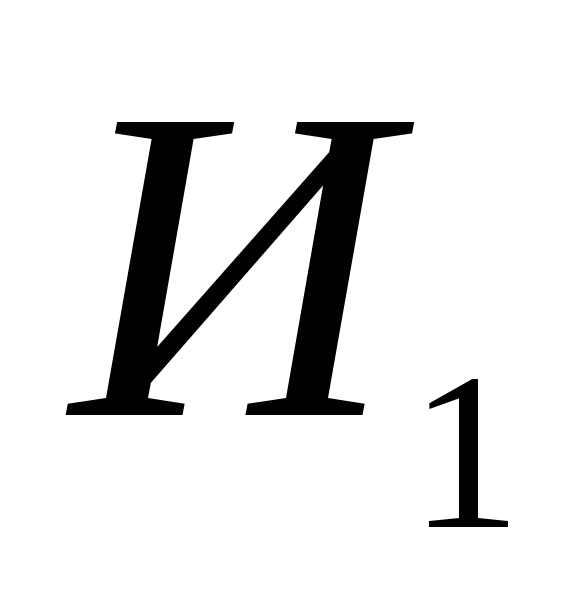
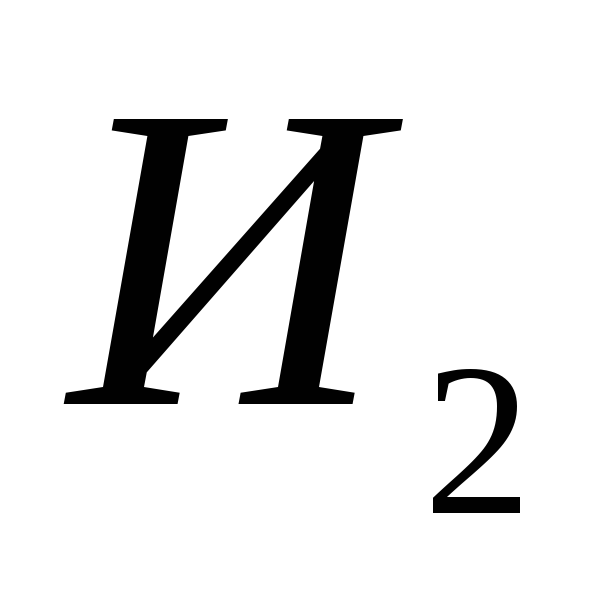
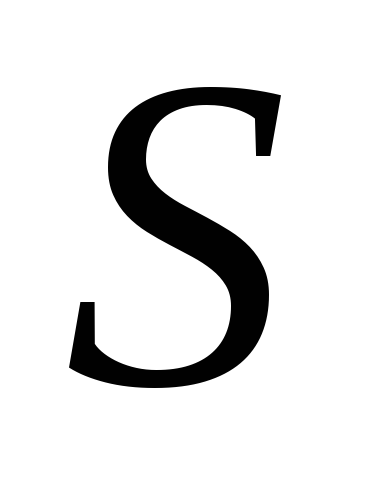
. (7.1)

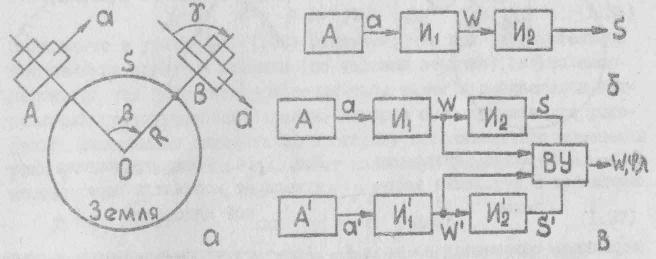
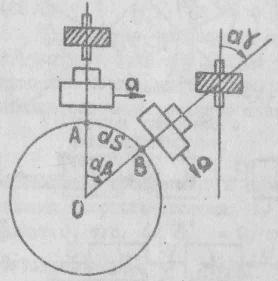
Рис. 7.1. Схема движения ЛА над землей и вычисления его путевой скорости и пройденного пути: – акселерометр,– первый и второй интеграторы

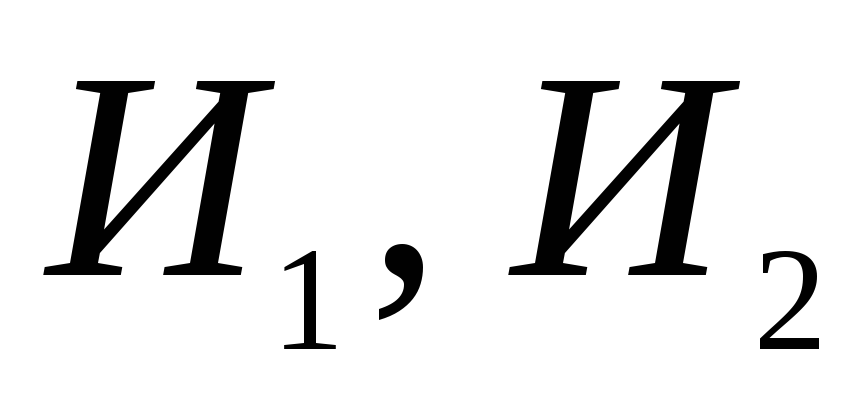
Истинная вертикаль за это время повернется на угол . На этот же угол(где– расстояние от центра Земли до ЛА) должна повернуться и платформа с акселерометром, чтобы она осталась в горизонтальном положении. Таким образом, зная координаты точки старта, можно определить координаты любой точкии вектор путевой скорости.

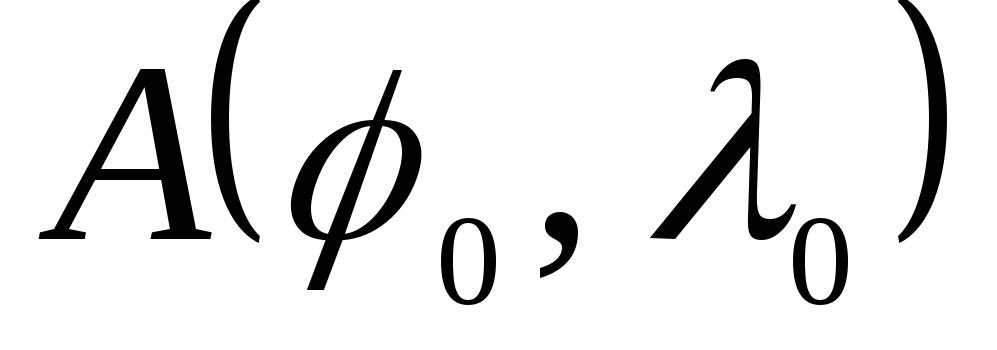
Если движение происходит не в одной плоскости, а на поверхности шара, то можно представить горизонтально стабилизированную платформу с двумя перпендикулярно расположенными акселерометрами, ориентированными по меридиану и параллели, и интеграторами. Ориентация акселерометров в азимутальной плоскости может быть произведена, например, с помощью гироскопов. Такая платформа с вычислительным устройством (рис. 7.1,в) позволяет определить абсолютную величину 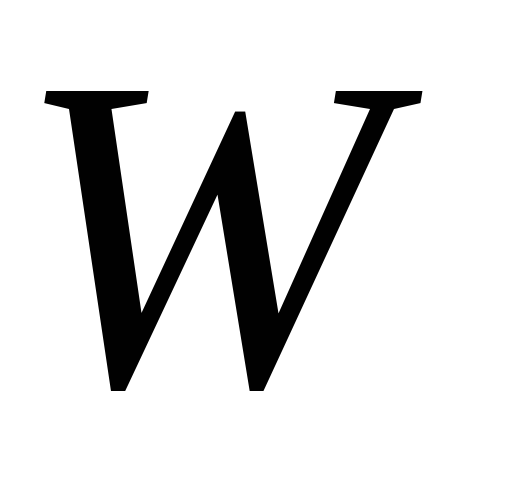, путевой угол движения ЛА, координаты,.

Рассмотрим принцип построения вертикали на ЛА. Эта задача является обратной задаче определения ,и. Если ЛА переместится из точки(рис. 7.1,а) с направлением вертикалив точкус направлением вертикали, то истинная вертикаль повернется на угол. Для того, чтобы платформа в точкезаняла горизонтальное положение, ее необходимо повернуть относительно первоначального положенияна угол. Таким образом, чтобы решить задачу построения вертикали, необходимо в любой момент времени знать величину углаи поворачивать платформу на угол. Приведенные выше соображения позволяют сделать вывод, что для получения ИНС необходимо объединить системы определения,,и построения вертикали.

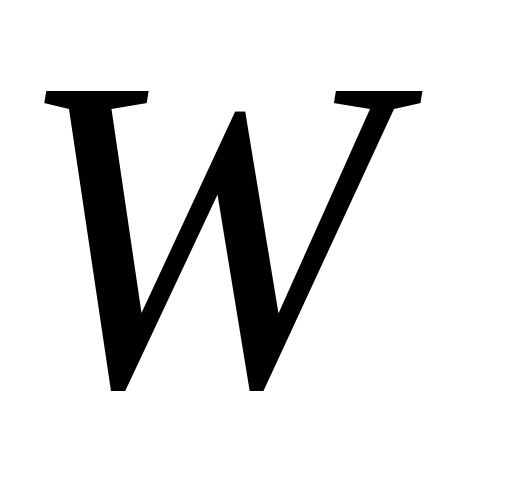
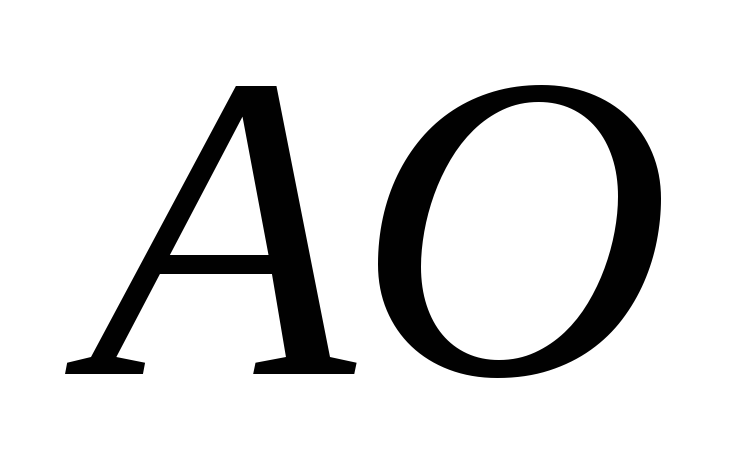
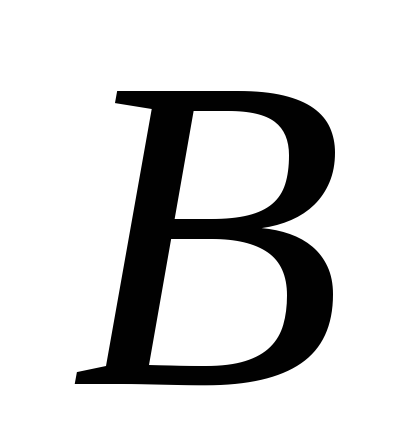
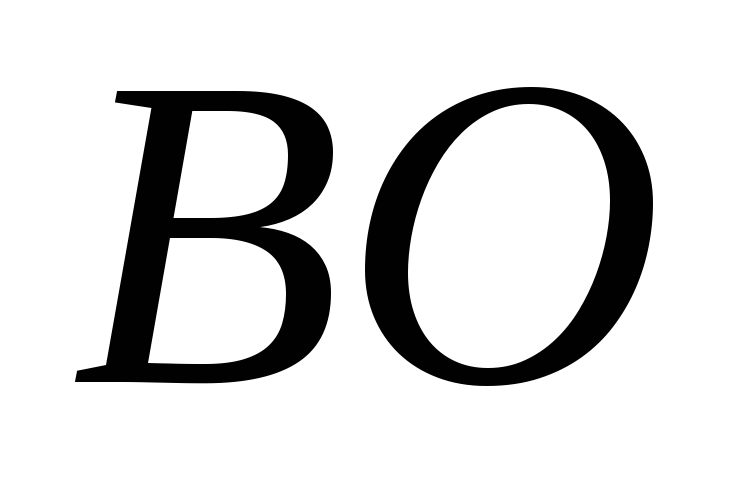
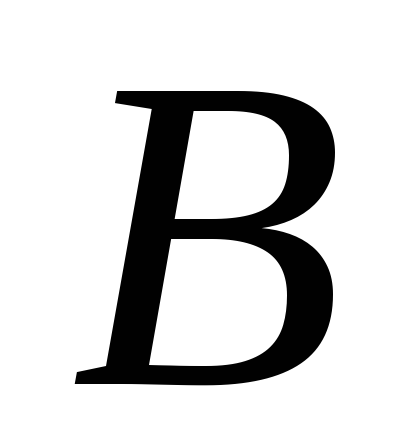
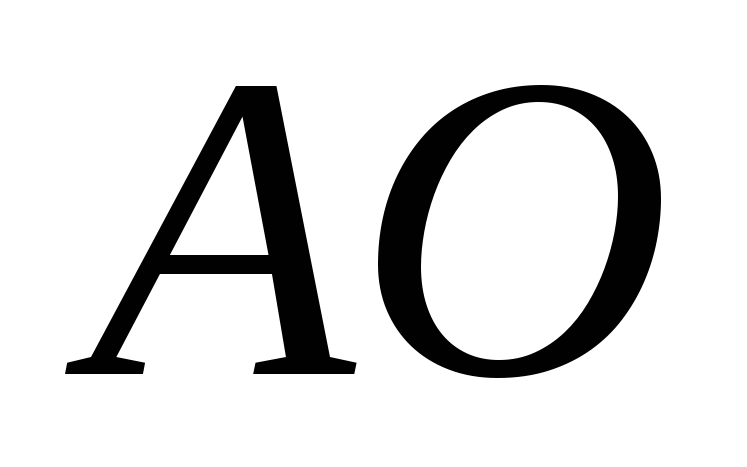
Такой вывод теоретически можно обосновать следующими рассуждениями. Пусть в точке (рис. 7.2) помещена платформа с акселерометром, которая может вращаться вокруг оси, перпендикулярной плоскости чертежа, и удерживается в заданном направлении в пространстве (например, в направлении) с помощью гироскопа. Поскольку процесс построения вертикали должен быть непрерывным, то вместо равенстваследует записать

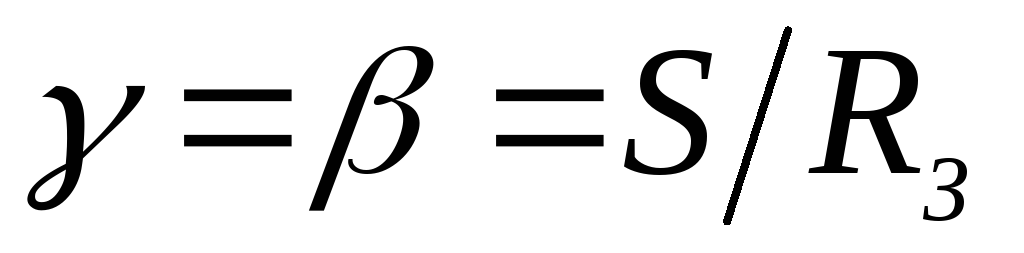
. (7.2)

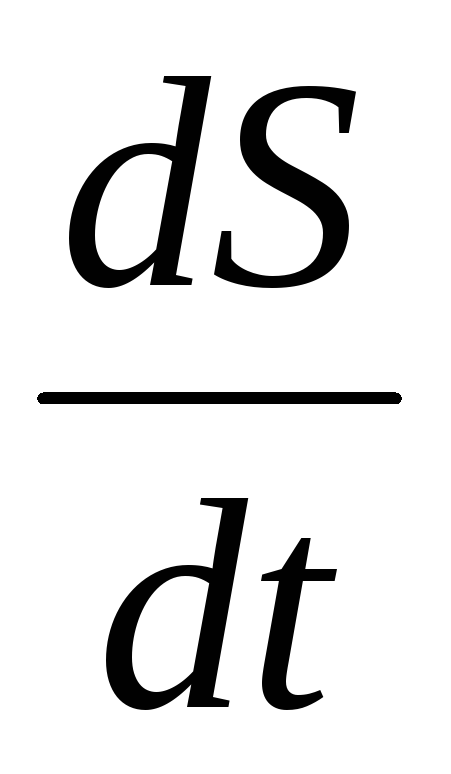
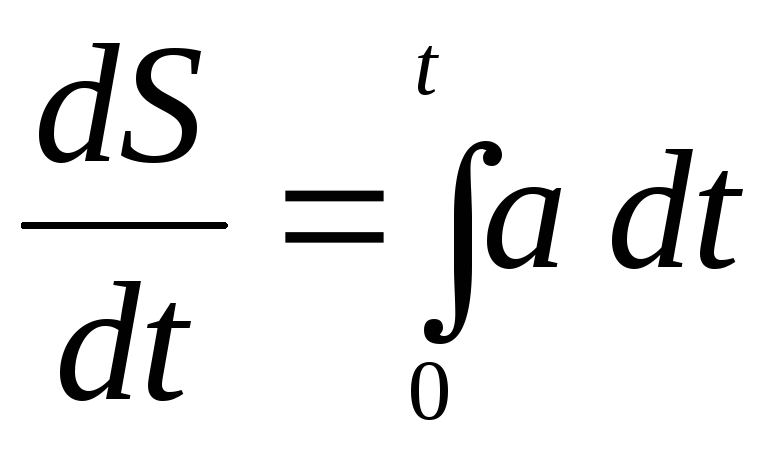
Величина определяется через ускорение, измеряемое акселерометром, тогда

. (7.3)

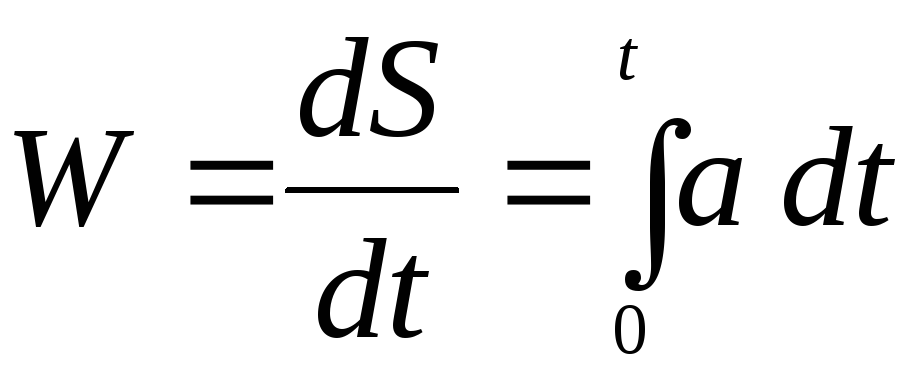
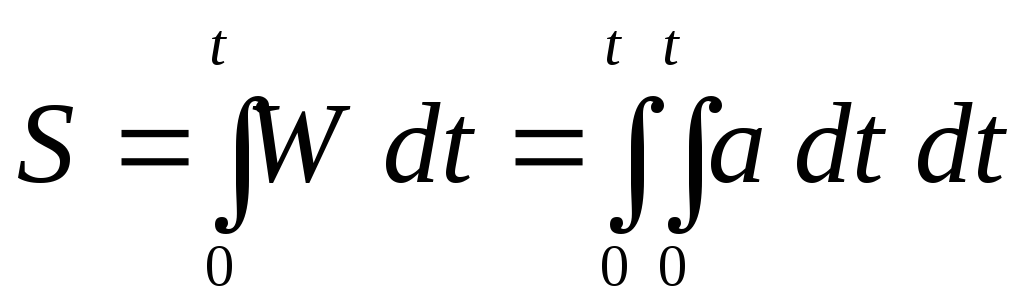
В результате будет построена устойчивая вертикаль, а также определены путевая скорость и координаты места ЛА,или пройденный путь.

Рис. 7.2. Схема построения вертикали и счисления координат

Рассмотренная система имеет свойства маятника. Если в точке (рис. 7.3) нормаль к платформе отклонится от истинной вертикали на малый угол, то акселерометр измерит составляющую земного ускорения

. (7.4)

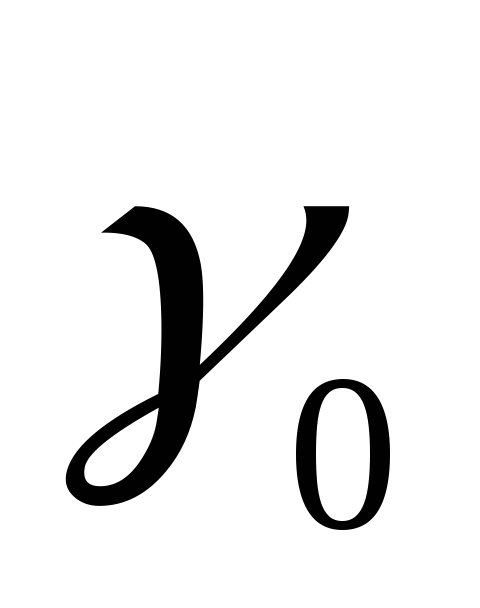
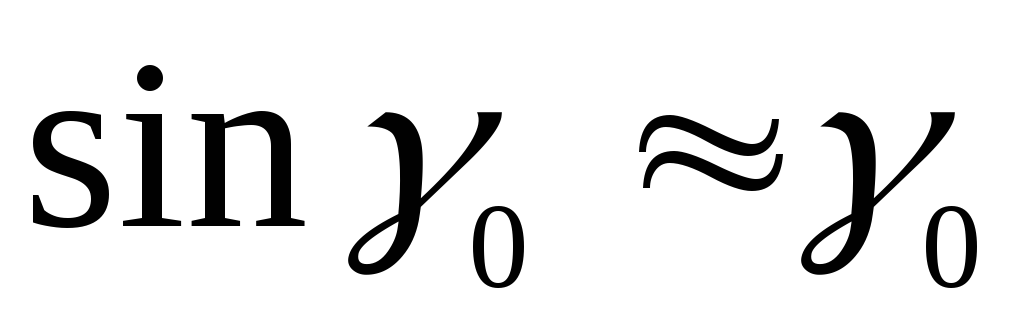
Так как угол имеет небольшую величину, то можно считать, тогдаи

. (7.5)

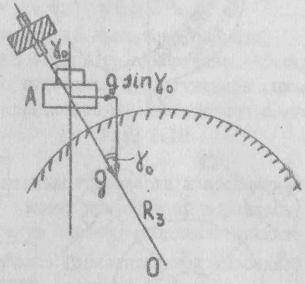
Рис. 7.3. Схема отклонения вертикали от нормали к горизонтальной плоскости

Продифференцировав (7.5), получим уравнение движения системы

. (7.6)

Это уравнение математического маятника относительно истинной вертикали места ЛА. Период колебаний вычисляется по формуле

мин. (7.7)

Получен период маятника Шулера при длине его подвеса =6371 км. Маятник Шулера имеет следующее свойство: его перемещение в пространстве равно в каждое мгновение дуге, представляющей собой смещение его подвеса вдоль поверхности Земли, т.е. маятник всегда поворачивается вокруг точки подвеса на тот же угол, что и вертикаль.

Обычную маятниковую вертикаль с периодом колебаний 84,4 мин создать невозможно. Невозмущаемая ускорениями вертикаль с периодом колебаний Шулера может быть построена при сочетании акселерометра и трехстепенного гироскопа, ошибка которого корректируется по сигналам, пропорциональным интегралу ускорения, измеряемого этим акселерометром, установленным на вертикальной оси гироскопа. Подобный способ коррекции носит название интегральной коррекции.

Источник

Инерциальные навигационные системы морских объектов, Лукьянов Д.П., Мочалов А.В., Одинцов А.А., Вайсгант И.Б., 1989

Инерциальные навигационные системы морских объектов, Лукьянов Д.П., Мочалов А.В., Одинцов А.А., Вайсгант И.Б., 1989.

В книге изложены принципы построения инерциальных навигационных систем ИНС различного типа, предназначенных прежде всего для решения задач навигации морских объектов. Приводятся сведения по приборному составу ИНС. Впервые в литературе по ИНС значительное внимание уделено перспективным чувствительным элементам — лазерным гироскопам и особенностям их использования в бесплатформенных ИНС. Большое внимание уделено анализу ошибок ИНС с учетом реальных моделей погрешностей чувствительных элементов.
Для специалистов, работающих в области морского приборостроения, прикладной гироскопии и систем управления подвижными объектами, а также для студентов и аспирантов соответствующих специальностей.

Принцип действия и состав ИНС.
Основные задачи, решаемые ИНС, — определение текущих координат движущегося объекта и выработка параметров его движения и углового положения. При этом используются только сведения о начальных координатах и угловом положении объекта и результаты обработки показаний входящих в состав ИНС чувствительных элементов.

Физические принципы, лежащие в основе работы ИНС, неразрывно связаны с решением основной задачи динамики: определение движения твердого тела исходя из знания его начального положения, скорости и действующих на него сил.

Рассмотрим гипотетический случай навигации по поверхности невращающейся Земли, представляющей собой идеальную сферу. Движение происходит в плоскости меридиана на север. При этом возможны три способа получения инерциальной информации.

ОГЛАВЛЕНИЕ.
ПРЕДИСЛОВИЕ.
Глава 1. ОБЩИЕ ПРИНЦИПЫ ПОСТРОЕНИЯ И ЧУВСТВИТЕЛЬНЫЕ ЭЛЕМЕНТЫ ИНС.
1.1. Принцип действия и состав ИНС.
1.2. Акселерометры, применяемые в ИНС.
1.3. Гироскопические чувствительные элементы.
1.4. Гиростабилизированные платформы.
1.5. Особенности использования морских ИНС и основные задачи теории ИНС.
1.6. Системы навигационных координат и их преобразование.
Глава 2. КЛАССИФИКАЦИЯ, УСТРОЙСТВО И РАБОТА МОРСКИХ ИНС.
2.1. Классификация ИНС и сравнительная оценка ИНС различных типов.
2.2. Полуаналитические ИНС.
2.3. ИНС геометрического типа.
2.4. ИНС аналитического типа.
2.5. Бесплатформенные ИНС.
Глава 3. ИНСТРУМЕНТАЛЬНЫЕ ПОГРЕШНОСТИ ЭЛЕМЕНТОВ ИНС.
3.1. Общие характеристики погрешностей.
3.2. Уходы неуправляемых гироскопов.
3.3. Особенности уходов управляемых гироскопов.
3.4. Погрешности поплавковых интегрирующих гироскопов.
3.5. Погрешности лазерных гироскопов.
3.6. Характер распределения составляющих ухода гироскопов во времени.
3.7. Способы повышения точности гироскопов.
Глава 4. ТЕОРИЯ ОШИБОК МОРСКИХ АВТОНОМНЫХ ИНС.
4.1. Постановка задачи.
4.2. Ошибки ИНС как ошибки моделирования инерциального трехгранника и построителя вертикали.
4.3. Связь между ошибками моделирования инерциального трехгранника и вертикали и ошибками ИНС.
4.4. Составление и преобразование уравнений ошибок ПА ИНС
4.5. Погрешности моделирования вертикали места в ПА ИНС.
4.6. Погрешности моделирования вертикали места с помощью ИНС ГТ.
4.7. Погрешности моделирования вертикали в ИНС АТ.
4.8. Особенности погрешности построителя вертикали на больших интервалах времени.
4.9. Погрешности моделирования инерциального трехгранника в ПА ИНС.
4.10. Погрешности моделирования инерциального трехгранника в ИНС на неуправляемых гироскопах.
4.11. Геометрические и кинематические погрешности гироориентаторов ИНС.
4.12. Ошибки бесплатформенных ИНС на лазерных гироскопах.
СПИСОК ЛИТЕРАТУРЫ.

Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:
Скачать книгу Инерциальные навигационные системы морских объектов, Лукьянов Д.П., Мочалов А.В., Одинцов А.А., Вайсгант И.Б., 1989 — fileskachat.com, быстрое и бесплатное скачивание.

Скачать djvu
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России. Купить эту книгу

Источник

Инерциальные навигационные системы морских объектов

В книге изложены принципы построения инерциальных навигационных систем ИНС различного типа, предназначенных прежде всего для решения задач навигации морских объектов. Приводятся сведения по приборному составу ИНС.
Впервые в литературе по ИНС значительное внимание уделено перспективным чувствительным элементам — лазерным гироскопам и особенностям их использования в бесплатформенных ИНС.
Большое внимание уделено анализу ошибок ИНС с учетом реальных моделей погрешностей чувствительных элементов.
Для специалистов, работающих в области морского приборостроения, прикладной гироскопии и систем управления подвижными объектами, а также для студентов и аспирантов соответствующих специальностей.
Оглавление
Предисловие
Глава 1. Общие принципы построения и чувствительные элементы ИНС
1.1. Принцип действия и состав ИНС
1.2. Акселерометры, применяемые в ИНС
1.3. Гироскопические чувствительные элементы
1.4. Гиростабилизированные платформы
1.5. Особенности использования морских ИНС и основные задачи теории ИНС
1.6. Системы навигационных координат и их преобразование
Глава 2. Классификация, устройство и работа морских ИНС
2.1. Классификация ИНС и сравнительная оценка ИНС различных типов
2.2. Полуаналитические ИНС
2.3. ИНС геометрического типа
2.4. ИНС аналитического типа
2.5. Бесплатформенные ИНС
Глава 3. Инструментальные погрешности элементов ИНС
3.1. Общие характеристики погрешностей
3.2. Уходы неуправляемых гироскопов
3.3. Особенности уходов управляемых гироскопов
3.4. Погрешности поплавковых интегрирующих гироскопов
3.5. Погрешности лазерных гироскопов
3.6. Характер распределения составляющих ухода гироскопов во времени
3.7. Способы повышения точности гироскопов
Глава 4. Теория ошибок морских автономных ИНС
4.1. Постановка задачи
4.2. Ошибки ИНС как ошибки моделирования инерциального трехгранника и построителя вертикали
4.3. Связь между ошибками моделирования инерциального трехгранника и вертикали и ошибками ИНС
4.4. Составление и преобразование уравнений ошибок ПА ИНС
4.5. Погрешности моделирования вертикали места в ПА ИНС
4.6. Погрешности моделирования вертикали места с помощью ИНС ГТ
4.7. Погрешности моделирования вертикали в ИНС AT
4.8. Особенности погрешности построителя вертикали на больших интервалах времени
4.9. Погрешности моделирования инерциального трехгранника в ПА ИНС
4.10. Погрешности моделирования инерциального трехгранника в ИНС на неуправляемых гироскопах
4.11. Геометрические и кинематические погрешности гироориентаторов ИНС
4.12. Ошибки бесплатформенных ИНС на лазерных гироскопах
Список литературы

• Прайс-Лист
• Контакты
• Доставка
• Карта сайта
• Работа у нас
• Акции и скидки

• Права потребителя
• Политика конфиденциальности
• F.A.Q.
• Наши награды
• Сертификаты
• Отзывы и пожелания

Instagram

Источник